转向架−车体−座椅系统垂向动力学模型及分析

于曰伟，周长城，赵雷雷



转向架−车体−座椅系统垂向动力学模型及分析

于曰伟，周长城，赵雷雷

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

应用系统工程的方法，将座椅系统与传统轨道客车系统作为一个整体大系统加以考察，建立轨道客车转向架−车体−座椅耦合系统垂向动力学模型，并推导模型的振动微分方程；根据转向架−车体−座椅耦合系统垂向振动微分方程组，通过变量变换，给出轨道客车转向架−车体−座椅系统垂向动力学模型的数值分析方法。通过与传统轨道客车垂向动力学模型得到的垂向随机响应进行对比，验证轨道客车转向架−车体−座椅耦合系统垂向动力学模型的正确性，该研究为轨道客车的振动特性分析及车辆悬挂系统参数和座椅悬置系统参数的优化设计提供了模型参考。

轨道客车；转向架−车体−座椅耦合系统；垂向动力学模型；数值分析方法；耦合振动分析

长期以来，在轨道车辆垂向动力学模型及分析的研究中，通常是将转向架−车体系统和座椅系统分开单独进行的[1−3]。翟婉明[4]建立了车辆−轨道垂向系统的统一模型，通过数值计算方法研究了系统在车轮扁疤下的车辆振动响应；陈果等[5]利用数值仿真方法分析了传统车辆模型与车辆−轨道耦合模型垂向随机振动响应之间的差异，表明2种模型在低频段作响应分析时，其结论相差甚微；郝建华 等[6−7]建立了铁道客车垂向广义Ruzicka隔振模型，应用评价函数对车辆垂向悬挂系统参数进行了优化；Stein等[8]通过建立轨道车辆座椅垂向动力学模型，对座椅振动响应进行了分析。事实上车辆各系统之间，即转向架−车体系统和座椅系统，是相互耦合且共同对车辆的动态性能起作用的[9−10]。因此，研究车辆振动形态时不应只考虑转向架−车体系统本身的特征，还应同时考虑与之相匹配的座椅系统特性，将这2个子系统统一成为一个大系统才能更好地反映轨道车辆的振动规律，使分析结果更加趋于客观实际。本文应用系统工程的方法，将座椅系统与转向架−车体系统作为一个整体大系统加以考察，建立轨道客车转向架−车体−座椅耦合系统垂向动力学模型；根据转向架−车体−座椅耦合系统垂向振动微分方程组，利用变量变换，对轨道客车转向架−车体−座椅系统垂向动力学模型的数值求解进行研究，并通过与传统轨道客车垂向动力学模型得到的垂向随机响应对比，对模型的正确性进行验证。

1 轨道客车转向架−车体−座椅系统垂向动力学模型

传统轨道车辆系统动力学研究中，通常忽略座椅系统与车辆系统相互耦合作用的影响，而将两者分开单独对其进行分析研究。为了充分反映轨道客车的振动形态，本文应用车辆耦合动力学原理，将座椅系统(图1(a)所示)与传统轨道客车系统(图1(b)所示)作为一个总体大系统，应用系统工程方法，建立了图1(c)所示的轨道客车转向架−车体−座椅系统垂向动力学模型，将模型1(c)中的座椅悬置刚度和阻尼去掉并将旅客质量折算到车体质量上即转化为传统轨道客车垂向动力学模型1(b)。其中，每节车厢中每排座位坐5人，共计排，旅客模型中，每排5人视为一个质量块，每节车厢共计个质量块；座椅与座椅之间的纵向间隔距离与实车保持一致；车厢中旅客满座，无站乘、空座现象。

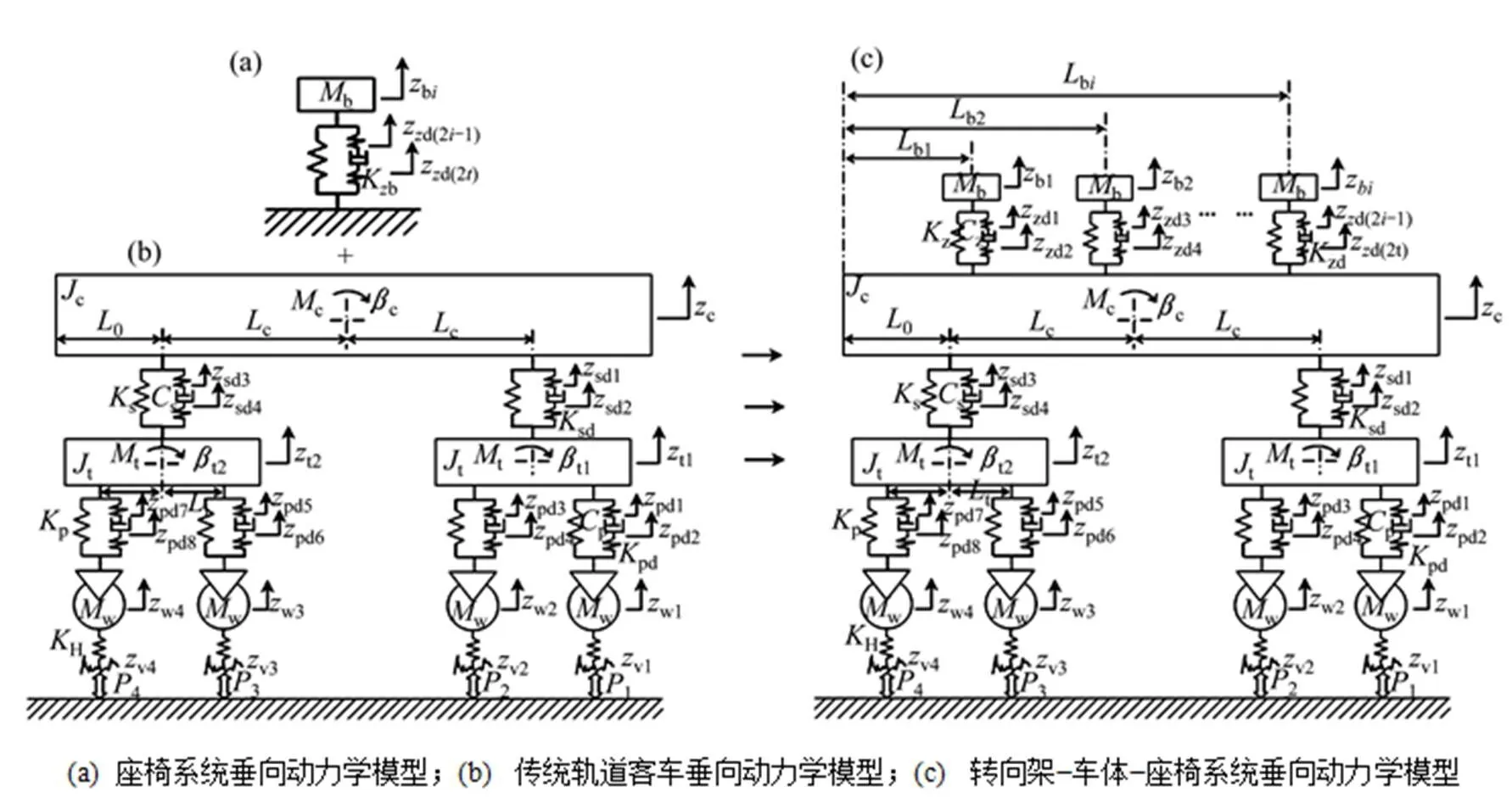
图1 轨道客车转向架−车体−座椅系统垂向动力学模型

图1中，b，Mc，t和w分别为每排旅客质量、车体质量、转向架构架质量和轮对质量，其中，b为每排旅客等效质量与座椅质量之和即b=0.83×5×旅客质量+5×座椅质量，c为车体结构质量与旅客腿部质量之和即c=车体结构质量+×0.17×5×旅客质量，为座椅排数，5为每排座位数，0.83为人体等效质量折算系数[11]；c和t分别为车体和转向架构架的点头转动惯量；p，s和z分别为一系悬挂、二系悬挂和座椅悬置的垂向等效刚度；p，s和z分别为一系悬挂、二系悬挂和座椅悬置的垂向等效阻尼；H为轮轨等效线性接触刚度；pd，sd和zd分别为一系垂向减振器、二系垂向减振器和座椅垂向减振器的橡胶节点刚度；bi为座椅安装间距，0为二系悬挂安装点至车厢端部的距离，c和t分别为车辆定距之半和转向架轴距之半；c，t1，t2和w1~w4分别为车体、前转向架构架、后转向架构架和轮对的垂向位移；c，t1和t2分别为车体、前转向架构架和后转向架构架的点头角位移；bi为座椅面的垂向位移；pd1~pd8，sd1~sd4和zd1~zd(2i)分别为一系垂向减振器、二系垂向减振器和座椅垂向减振器的两端垂向位移；v1~v4为轨道高低不平顺激励；1~4为轮轨作用力。其中，轮轨等效线性接触刚度[12−13]

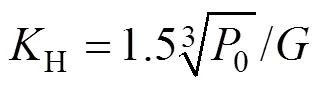
式中：0为轮轨静态作用力；为轮轨接触常数，对于锥形踏面车轮=4.57−0.149×10−8 m/N2/3，磨耗型踏面车轮=3.86−0.115×10−8 m/N2/3，其中，为车轮半径。

v2，v3和v4可用v1表示为

式中：表示时间；为时间滞后；1=2t/，2=2c/，3=2(t+c)/；为车辆运行速度。

2 轨道客车转向架−车体−座椅系统的数学模型

轨道客车转向架−车体−座椅垂向振动系统是一个多刚体动力系统，其振动微分方程可通过对各个刚体逐一应用牛顿第二定律获得。

1) 座椅沉浮运动

2) 车体沉浮运动

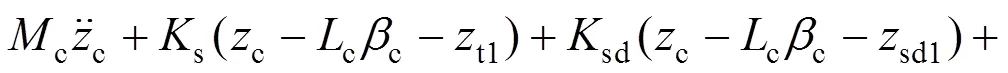
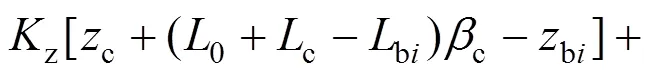
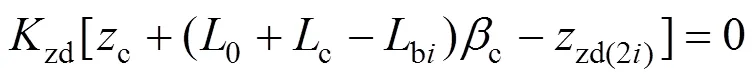
3) 车体点头运动

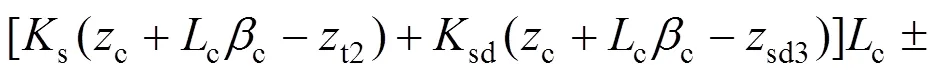
4) 前转向架构架沉浮运动

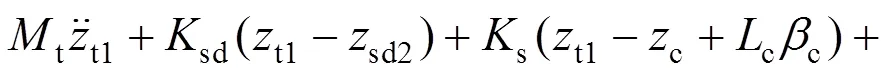
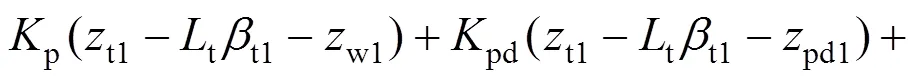
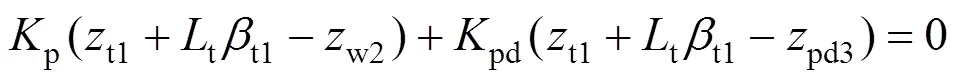
5) 前转向架构架点头运动

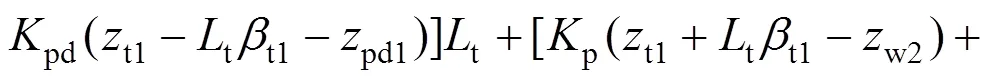
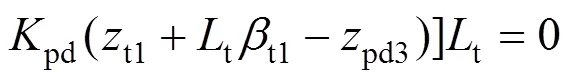
6) 后转向架构架沉浮运动

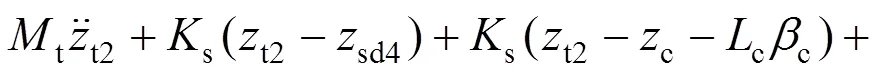
7) 后转向架构架点头运动

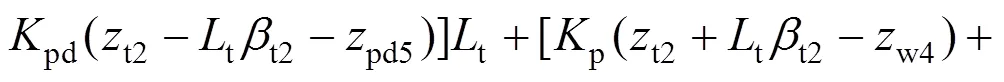
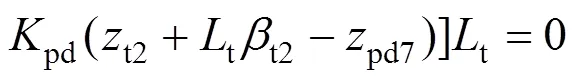
8) 第1轮对沉浮运动

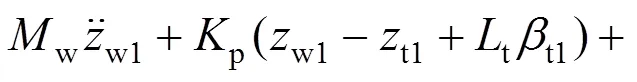
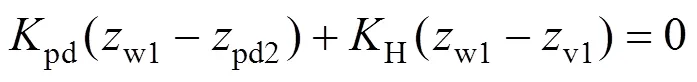
9) 第2轮对沉浮运动

10) 第3轮对沉浮运动

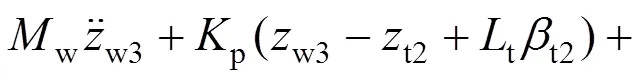
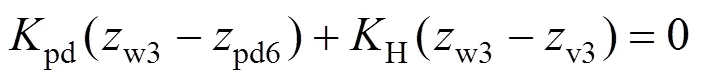
11) 第4轮对沉浮运动

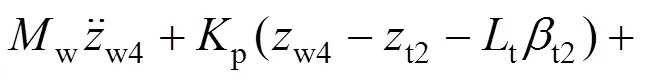
12) 座椅减振器端部力平衡方程

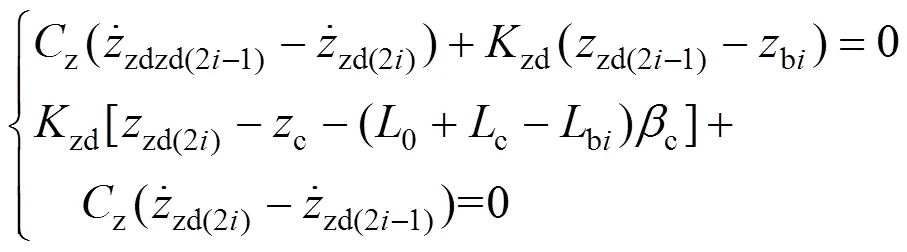
13) 二系减振器端部力平衡方程

14) 一系减振器端部力平衡方程

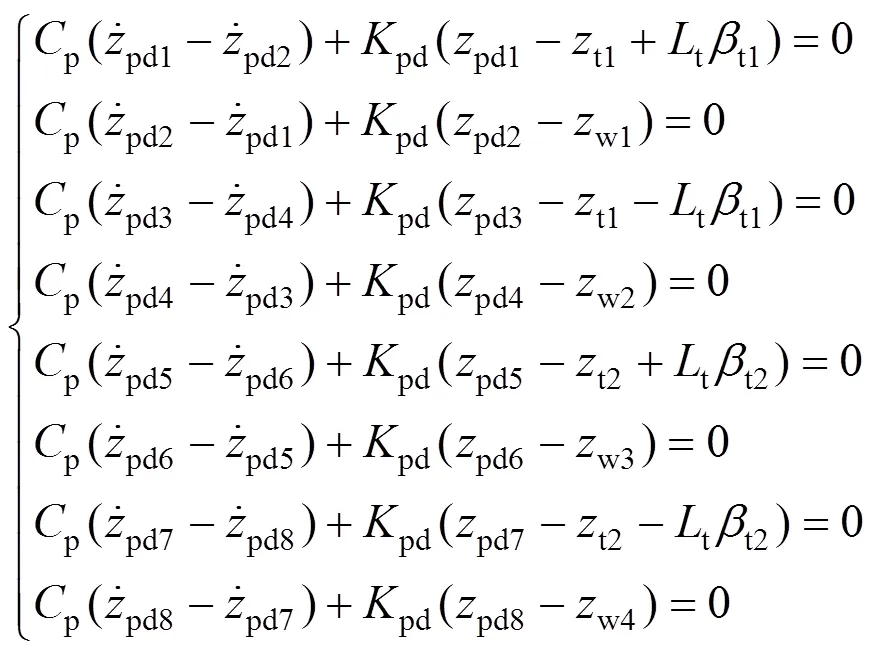
由上述可见，轨道客车转向架−车体−座椅系统垂向动力学方程组的阶数为：22+3。

3 轨道客车转向架−车体−座椅系统垂向动力学模型的数值分析方法

分析振动微分方程组(3)~(16)可知，方程中含有(10+)个加速度变量的二阶微分方程，同时含有(12+2)个速度变量的一阶微分方程，如不通过变换，无法将该非常规振动微分方程组表示为可求解形式的状态空间方程[14]。因此，为了便于求解，令Δz1=zd1−zd2，…，Δzi=zd(2i−1)−zd(2i)，Δs1=sd1−sd2，Δs2=sd3−sd4，Δp1=pd1−pd2，Δp2=pd3−pd4，Δp3=pd5 −pd6，Δp4=pd7−pd8，由此可得如下变换关系

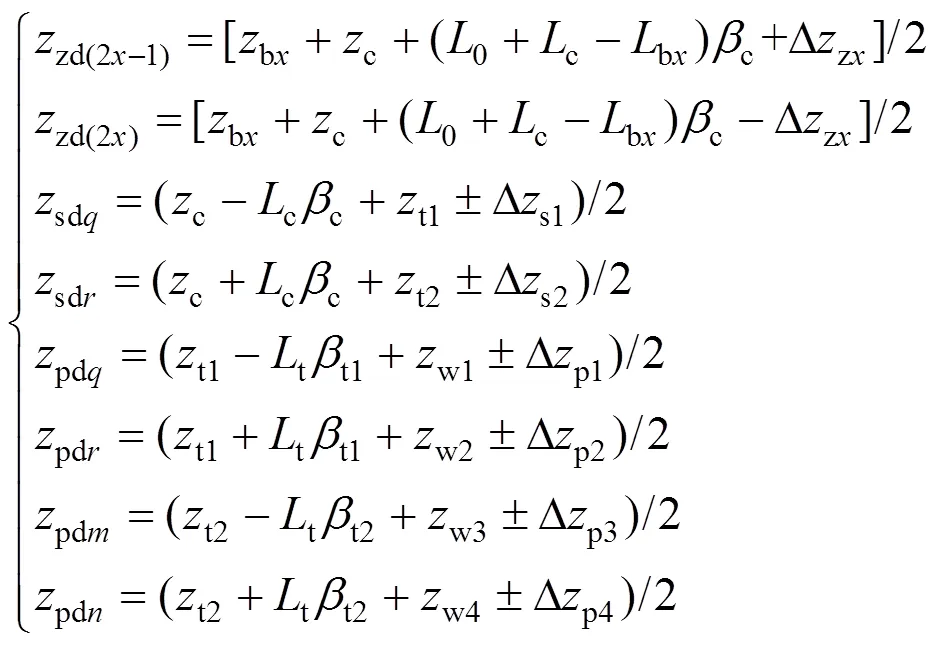
式中：=1，2，…，；=1，2，=3，4，=5，6，=7，8；仅当=1，=3，=5，=7时，式中取“＋”。

将式(17)代入振动微分方程组(3)~(16)，并将其表示为矩阵形式，可得

；

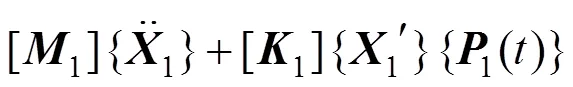
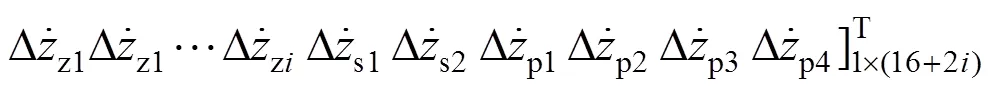
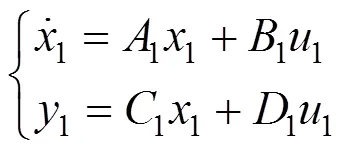
式中：系统矩阵

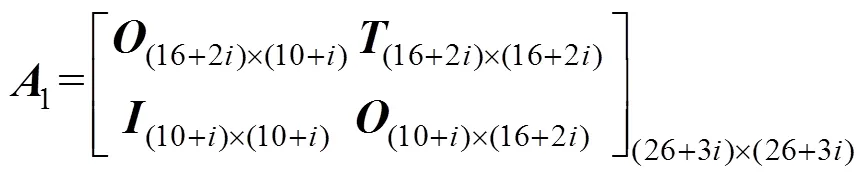
输入矩阵

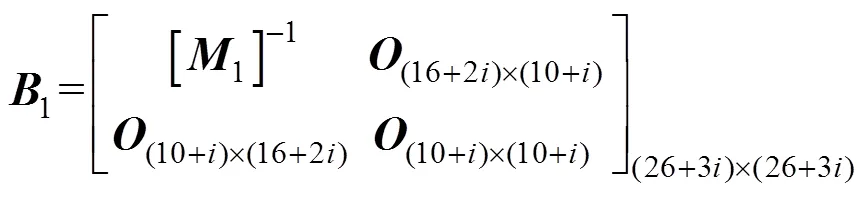
输出矩阵

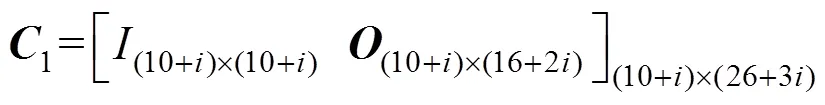
输出向量

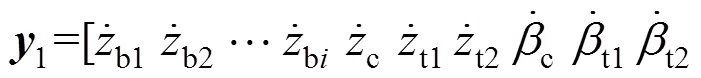
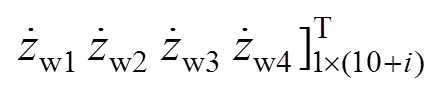
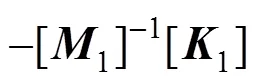
根据状态空间方程式(19)，利用MATLAB编写计算程序并应用变步长四阶龙格—库塔法进行方程的求解，可得到轨道客车转向架−车体−座椅系统垂向动力学模型的响应值。

4 轨道客车转向架−车体−座椅系统垂向动力学模型的数值仿真验证

为了检验所建立轨道客车转向架−车体−座椅系统垂向动力学模型的正确性，以某CRH2轨道客车为应用实例，运用轨道客车转向架−车体−座椅系统垂向动力学模型，在轨道高低不平顺激扰作用下进行车辆动态数值仿真，并与传统轨道客车垂向动力学模型进行垂向随机响应比较。车辆系统参数取值见表1，其中，每节车厢中每排座位坐5人，共计20排，座椅质量为20 kg，车体结构质量为39 600 kg，旅客平均体重为65 kg，列车采用磨耗型踏面车轮，列车运行速度为300 km/h。

以德国高速轨道高低不平顺功率谱密度作为模型的输入激励[15]，其空间频率解析表达式为

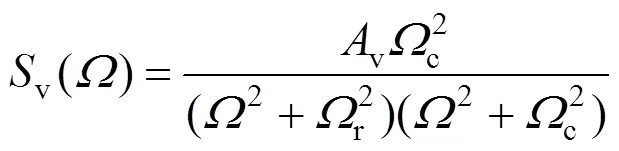
式中：v()为高低不平顺功率谱密度；为轨道不平顺的空间频率；v为轨道粗糙度系数；c和r为截断空间频率；各已知参数值见表2。

其中，低干扰谱适合250 km/h及以上车速，高干扰谱适合250 km/h以下车速。

表1 轨道客车系统参数值

表2 德国轨道高低不平顺参数值

根据德国轨道高低不平顺功率谱密度解析表达式(20)，采用文献[15]所提供的时频转换方法，将频域激励转换为时域样本，作为系统的输入，对轨道客车转向架−车体−座椅系统垂向动力学模型和传统轨道客车垂向动力学模型的垂向随机振动响应进行数值仿真，得到的车体垂向振动加速度及前转向架构架和后转向架构架垂向振动加速度功率谱密度仿真对比结果，如图2~4所示。

图2 车体垂向振动加速度功率谱密度

图3 前转向架构架垂向振动加速度功率谱密度

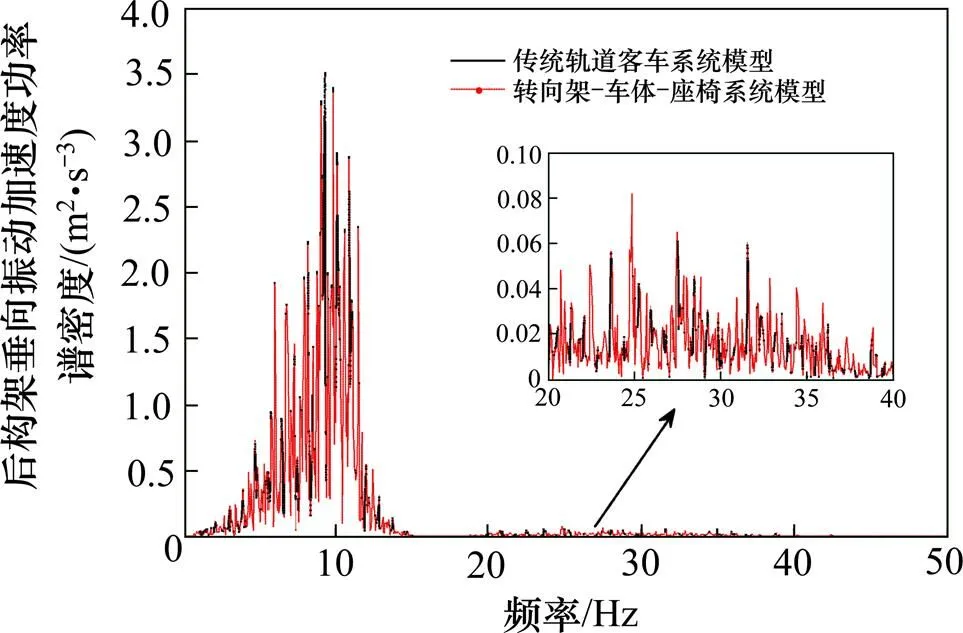
图4 后转向架构架垂向振动加速度功率谱密度

从图2~4可以看出，2种模型得到的垂向随机响应功率谱基本吻合，其中转向架构架的垂向振动加速度功率谱在整个频率段范围内几乎完全一致。对于车体的垂向振动，在4.0~12.0 Hz之内有一定的差异，但在0~4.0 Hz范围内，两者的功率谱密度曲线几乎完全重合，产生该差异的原因在于座椅系统引起的较高频率的响应成分迭加于基响应(参见图2中传统轨道客车系统模型响应)之上，使得转向架−车体−座椅系统模型所得响应中含有较高频率的响应成分，导致2种模型的振动响应在较高频率(4.0~12.0 Hz)处出现一定差异，这显然是转向架−车体系统和座椅系统共同作用的结果。综上所述，通过对两种模型垂向随机振动响应的比较，可以看出，尽管两者之间存在一定的差异，但其计算结果基本一致，该结论说明转向架−车体−座椅系统之间是相互耦合、相互影响的，更有力地证明了轨道客车转向架−车体−座椅系统垂向动力学模型的正 确性。

5 轨道客车转向架−车体−座椅系统垂向动力学模型的工程应用

传统座椅垂向动力学模型和轨道客车垂向动力学模型中，通常将座椅系统和车辆系统分开，单独对其进行研究，因此在分析座椅系统和车辆系统的振动形态时与实际情况存在较大差异，且存有诸多不便。

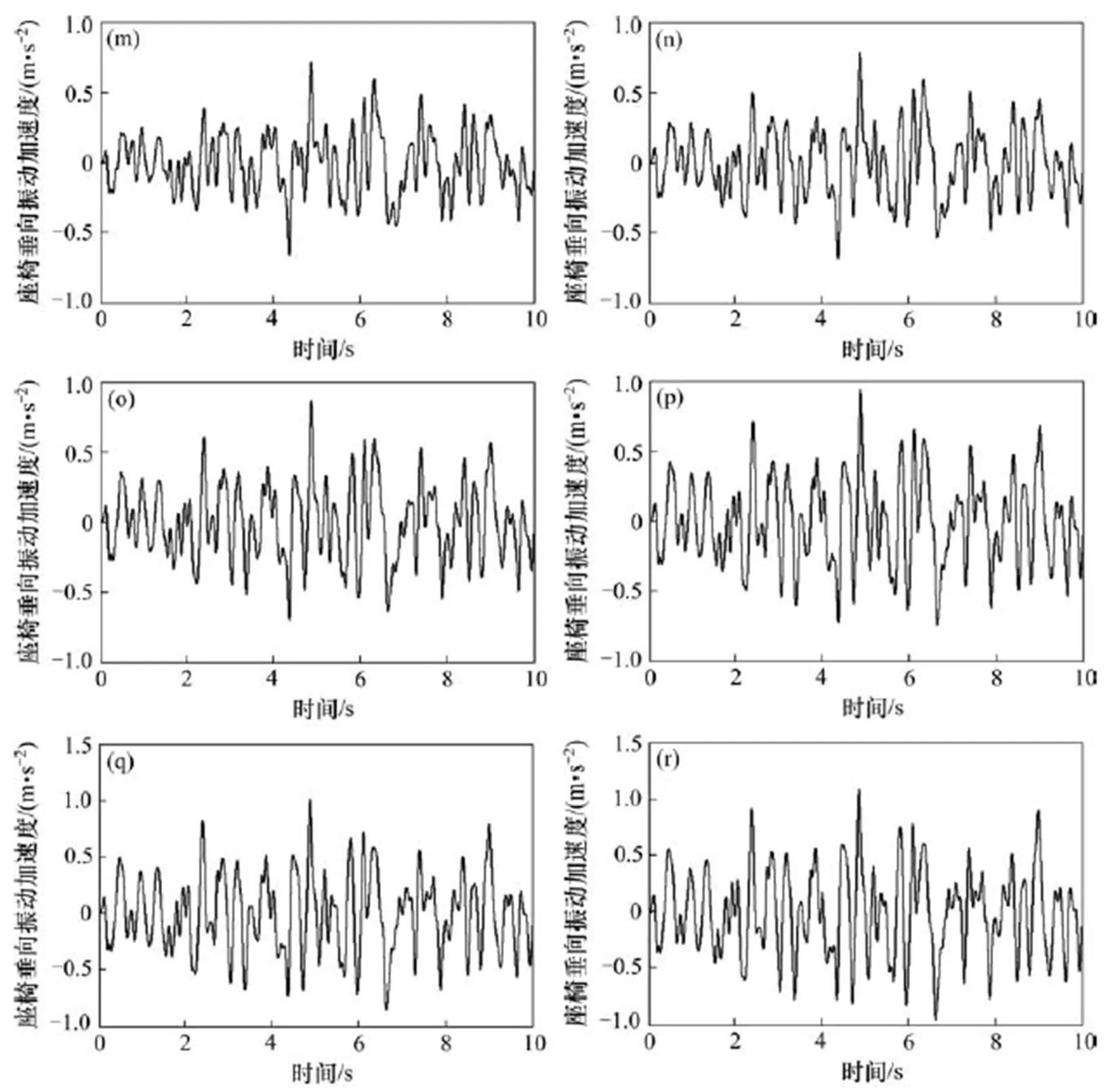
应用本文建立的轨道客车转向架−车体−座椅系统垂向动力学模型，可以从大系统的数值模拟角度，揭示车辆系统与座椅系统在垂向随机激扰作用下的耦合振动形态，还可用于车辆悬挂系统参数和座椅悬置系统参数的优化设计。例如，车辆在运行过程中，车体与座椅之间将产生连续的相互动作用力，向上传递给座椅和人体，向下施加于车体，引起车辆系统与座椅系统产生各自的振动，而这种振动又互相反馈，互为因果，助长了车体与座椅之间的相互动力作用。据此，可利用优化设计理论，对座椅悬置系统参数进行优化设计。图5给出了表1所示轨道客车座椅垂向振动加速度的数值模拟结果，由此可知，不同安装位置处的座椅垂向振动情况有所差异，在分析座椅振动形态时应综合考虑安装位置的影响。

随着铁路旅客运输的不断发展，对轨道客车的乘坐舒适性和运行安全性提出了更高的设计要求。应用车辆耦合动力学原理，将座椅系统和车辆系统置于同一模型下进行研究，可进一步提高轨道客车的运行品质，为轨道客车振动特性分析、车辆悬挂系统参数和座椅悬置系统参数设计提供模型参考。

6 结论

1) 应用系统工程的方法，将座椅系统与传统轨道客车系统作为一个整体大系统加以考察，建立了轨道客车转向架−车体−座椅耦合系统垂向动力学模型，使分析结果更加接近实际。

2) 根据转向架−车体−座椅耦合系统垂向振动微分方程组，通过变量变换，给出了轨道客车转向架−车体−座椅系统垂向动力学模型的数值分析方法，为非常规振动微分方程的数值求解提供了有效参考。

3) 通过与传统轨道客车垂向动力学模型得到的垂向随机响应进行对比，对轨道客车转向架−车体−座椅耦合系统垂向动力学模型的正确性进行了验证，该研究为轨道客车座椅系统和车辆系统的振动特性分析，及车辆悬挂系统参数和座椅悬置系统参数的优化设计提供了模型参考。

[1] 王福天. 车辆系统动力学[M]. 北京: 中国铁道出版社, 1994. WANG Futian. Vehicle system dynamics[M]. Beijing: China Railway Press, 1994.

[2] Garg V K, Dukkipati R V. Dynamics of vehicle system dynamics[M]. Toronto: Academic Press, 1984.

[3] 杨岳, 张晓峰, 张兆丰, 等. 面向运行平稳性的铁道车辆悬挂参数灵敏度分析[J]. 铁道科学与工程学报, 2014, 11(2): 116−120. YANG Yue, ZHANG Xiaofeng, ZHANG Zhaofeng, et al. Sensitivity analysis of railway vehicle suspension parameters on riding stability[J]. Journal of Railway Science and Engineering, 2014, 11(2): 116−120.

[4] 翟婉明. 车辆−轨道垂向系统的统一模型及其耦合动力学原理[J]. 铁道学报, 1992, 14(3): 10−21. ZHAI Wanming. The vertical model of vehicle-track system and its coupling dynamics[J]. Journal of the China Railway Society, 1992, 14(3): 10−21.

[5] 陈果, 翟婉明, 蔡成标, 等. 传统车辆模型与车辆−轨道耦合模型的垂向随机振动响应分析及比较[J]. 铁道学报, 1999, 21(5): 70−74. CHEN Guo, ZHAI Wanming, CAI Chengbiao, et al. Comparison on vertical random vibration responses of traditional vehicle model with vehicle/track coupling model[J]. Journal of the China Railway Society, 1999, 21(5): 70−74.

[6] 郝建华, 曾京, 邬平波. 铁道客车垂向随机减振及悬挂参数优化[J]. 铁道学报, 2006, 28(6): 35−40. HAO Jianhua, ZENG Jing, WU Pingbo. Optimization of vertical random vibration isolation and suspension parameters of railway passenger car systems[J]. Journal of the China Railway Society, 2006, 28(6): 35−40.

[7] 郝建华, 曾京, 邬平波. 铁路车辆垂向减振与悬挂系统参数优化[J]. 交通运输工程学报, 2005, 5(4): 10−14. HAO Jianhua, ZENG Jing, WU Pingbo. Vertical vibration isolation and suspension parameter optimization of railway vehicle[J]. Journal of Traffic and Transportation Engineering, 2005, 5(4): 10−14.

[8] Stein G J, Mucka P, Gunston T P, et al. Modelling and simulation of locomotive driver’s seat vertical suspension vibration isolation system[J]. International Journal of Industrial Ergonomics, 2008, 38(5−6): 384−395.

[9] Hidehisa Y, 段书华. 基于旅客-车体耦合振动的车辆振动分析[J]. 国外铁道车辆, 2010, 47(2): 16−22. Hidehisa Y, DUAN Shuhua. Vibration analysis of railway vehicle by evaluating the coupled passenger-carbody vibration[J]. Foreign Rolling Stock, 2010, 47(2): 16−22.

[10] 张济民, 胡用生, 陆正刚. 轨道车辆运行过程中人体振动仿真研究[J]. 振动与冲击, 2007, 26(10): 76−80.ZHANG Jimin, HU Yongsheng, LU Zhenggang. Vibration simulation of human body on running railway vehicle[J]. Journal of Vibration and Shock, 2007, 26(10): 76−80.

[11] 侯之超, 高江华, 何乐. 坐姿人体垂向振动特性及其三自由度模型参数[J]. 哈尔滨工程大学学报, 2011, 32(9): 1223−1227. HOU Zhichao, GAO Jianghua, HE Le. Vertical vibration characteristics of seated human bodies and the parameters of a biodynamic model with three degrees of freedom[J]. Journal of Harbin Engineering University, 2011, 32(9): 1223−1227.

[12] 陈果. 车辆—轨道耦合系统随机振动分析[D]. 成都: 西南交通大学, 2000. CHEN Guo. The analysis on random vibration of vehicle/track coupling system[D]. Chengdu: Southwest Jiaotong University, 2000.

[13] 李双, 余衍然, 陈玲, 等. 随机悬挂参数下轨道车辆平稳性的全局灵敏度分析[J]. 铁道学报, 2015, 37(8): 29− 35.LI Shuang, YU Yanran, CHEN Ling, et al. Global sensitivity analysis on the ride quality of railway vehicle with stochastic suspension parameters[J]. Journal of the China Railway Society, 2015, 37(8): 29−35.

[14] 曾京, 邬平波. 减振器橡胶节点刚度对铁道客车系统临界速度的影响[J]. 中国铁道科学, 2008, 29(2): 94−98. ZENG Jing, WU Pingbo. Influence of the damper rubber joint stiffness on the critical speed of railway passenger car system[J]. China Railway Science, 2008, 29(2): 94− 98.

[15] 翟婉明. 车辆−轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015. ZHAI Wanming. Vehicle-track coupled dynamics[M]. 4th ed. Beijing: Science Press, 2015.

Vertical dynamic model and analysis of bogie-body-seat coupling system

YU Yuewei, ZHOU Changcheng, ZHAO Leilei

(School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

Based on the theory of system engineering, taking the seat system and traditional railway vehicle system as a whole system, a vertical dynamic model of bogie-body-seat coupling system for railway vehicle was established, and the vibration differential equation model was deduced; according to the vertical vibration differential equation group of bogie-body-seat coupling system, through variable transformation, a numerical analysis method of bogie-body-seat coupling system vertical dynamic model of railway vehicle was built. By comparing with the vertical random response of traditional railway vehicle vertical model, the vertical dynamic model of the bogie-body-seat coupling system was verified. This research provides an effective reference model for the vehicle vibration characteristics analysis, and for the design of vehicle suspension parameter system and seat suspension system parameter system.

railway vehicle; bogie-body-seat coupling system; vertical dynamic model; numerical analysis method; coupling vibration analysis

U260.11

A

1672 − 7029(2018)01 − 0196 − 10

2016−12−28

国家自然科学基金资助项目(51575325)；山东省重点研发计划资助项目(2015GGX105006)

周长城(1962−)，男，山东泰安人，教授，博士，从事机车车辆动力学及控制研究；E−mail：greatwall@sdut.edu.cn