黄土边坡自振特性影响因素分析

孙纬宇，严松宏，欧尔峰，宋旭辉



黄土边坡自振特性影响因素分析

孙纬宇1, 2，严松宏1, 3，欧尔峰1, 2，宋旭辉1, 2

(1. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2. 兰州交通大学 土木工程学院，甘肃 兰州 730070；3. 甘肃省轨道交通力学应用工程实验室，甘肃 兰州 730070)

边坡的动力特性是影响其动力响应的内在因素，对边坡的动力稳定性起着重要作用。运用ANSYS大型通用有限元软件对不同坡高和不同坡度的三维黄土边坡进行模态分析，探讨坡高和坡度对黄土边坡自振频率的影响。研究结果表明：各坡高和坡度条件下，黄土边坡的前10阶自振频率随频率阶数的增大而增大；坡度对各阶自振频率的影响相对较小，坡高对各阶自振频率的影响较大，随着坡度的增大，基频呈增大趋势，但增幅不大，同一坡高不同坡度时基频的相对变化率的最大值仅为6.80%；坡高对基频的影响较大，随着坡高的增大基频呈减小趋势，相同坡度不同坡高时基频相对变化率的范围为49.95%~50.02%。研究可为黄土边坡抗震设计时避免共振的发生提供一定的参考。

黄土边坡；自振特性；模态分析；ANSYS

我国是世界上黄土分布面积最广、层厚最大、成因类型复杂的地区，分布面积达64万km2，约占国土面积的6.6%，世界黄土覆盖面积的4.9%。据统计，黄土高原范围内Ⅵ度以上地震烈度区超过该区域面积的80%，其中Ⅶ度和Ⅷ度区约占60%，可见黄土高原地区地为强震多发区[1]。而地震是触发黄土边坡失稳的重要原因之一[2]，因此，研究地震作用下黄土边坡的稳定性是十分必要的。地震动作用下边坡的稳定性，主要应从地震动特性和边坡自身特性来考虑。其中地震动特性一般包括地震动强度、频谱特性和持时等3个方面[3]。边坡自身性质则要考虑到边坡的地质背景、岩体的结构类型、岩性组合、边坡高度和坡度及坡型、水文地质条件等因素的影响[4]。言志信等[5−11]通过数值计算和模型试验研究了黄土边坡的动力响应规律以及失稳破坏特征，得出了一些有益的结论。众所周知，当输入边坡的地震动卓越周期与边坡的自振周期相接近时，边坡的动力反应显著增强。同时，通过谐响应分析研究了单、双向地震动作用下边坡的共振特性与固有频率特性，认为第一阶固有频率处的共振为水平向振动，幅值最大，造成的危害也最大；张学东等[12]对岩质边坡的自振特性进行了研究，得出了随坡高的增加，边坡的自振频率呈降低的趋势；杨巨文等[13]用振动台模型试验和数值模拟的方法得出了含弱层岩质边坡的固有频率。由此可见，边坡的自振特性在边坡的动力稳定性分析方面起着重要的作用。而以往多数研究均是针对岩质边坡在某一特定的坡高和坡度下进行的，对于不同坡高和坡度条件下的黄土边坡自振特性的研究还很少见到，本文将从坡高和坡度两个方面来探讨其对黄土边坡自振频率的影响。

1 计算模型及参数的选取

为了探讨黄土边坡自震特性的一般规律，根据张鲁渝等[14]提出的最佳边坡模型尺寸要求，即边坡模型的坡脚到前缘边界的距离为坡高的1.5倍，坡肩到后缘边界的距离为坡高的2.5倍，上、下边界总高为坡高的2.0倍。本次计算中三维边坡模型尺寸均采用这一标准，其中边坡宽度取2.0倍的坡高，计算所采用的概化模型图如图1所示。

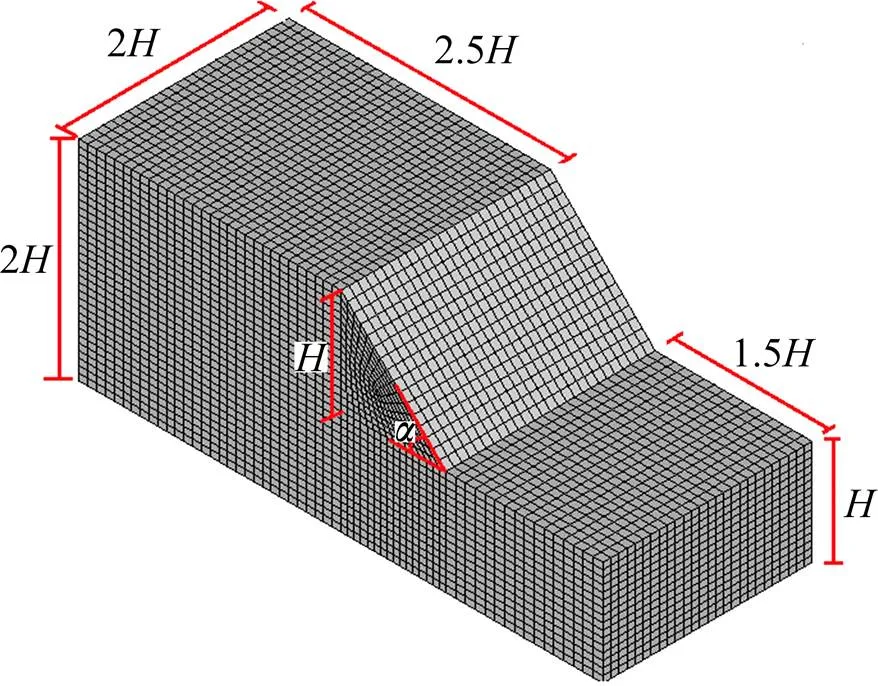
图1 边坡概化模型示意图

采用ANSYS建立如图1所示的三维边坡有限元模型，模型的侧边界采用垂直于侧面的水平向约束，底边界采用全约束。土体用solid45单元进行模拟，分别计算30，40，50和60 m坡高分别在30°，40°，50°，60°和70°时边坡的前10阶自振频率。其中计算参数可根据梁庆国等[15]对几个兰州周边地区黄土的物理力学特性的试验研究选取，参数如表1所示。

表1 数值模型材料物理力学参数

2 计算原理

模态分析用于确定结构的动力特性，即结构的自振频率和振型等。将上述的边坡计算模型视为多自由度体系，其无阻尼自由振动的微分方程可表示为[16]：

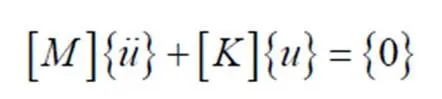
在特定的初始条件下，体系按同一频率做简谐振动，因此，无阻尼自由振动的方程基本解形式可写为：

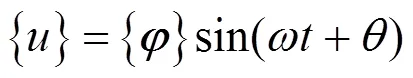
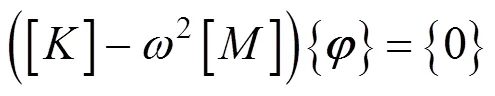
则体系的频率方程或特征方程为：

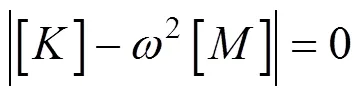
ANSYS提供了7种模态分析方法，分别是分块兰索斯法、子空间迭代法、缩减法、Power Dynamics法、非对称法、阻尼法和QR阻尼法，本次计算中采用ANSYS默认的分块兰索斯法进行模态分析。

3 坡度和坡高对黄土边坡自振特性的影响

3.1 坡度对黄土边坡自振特性的影响

在ANSYS中分别建立30，40，50和60 m坡高，不同坡度的三维黄土边坡模型进行模态分析，得到了各个坡高不同坡度下边坡的前10阶自振频率，对各个坡高不同坡度条件下前10阶自振频率绘制频率变化曲线，曲线的变化趋势如图2所示。

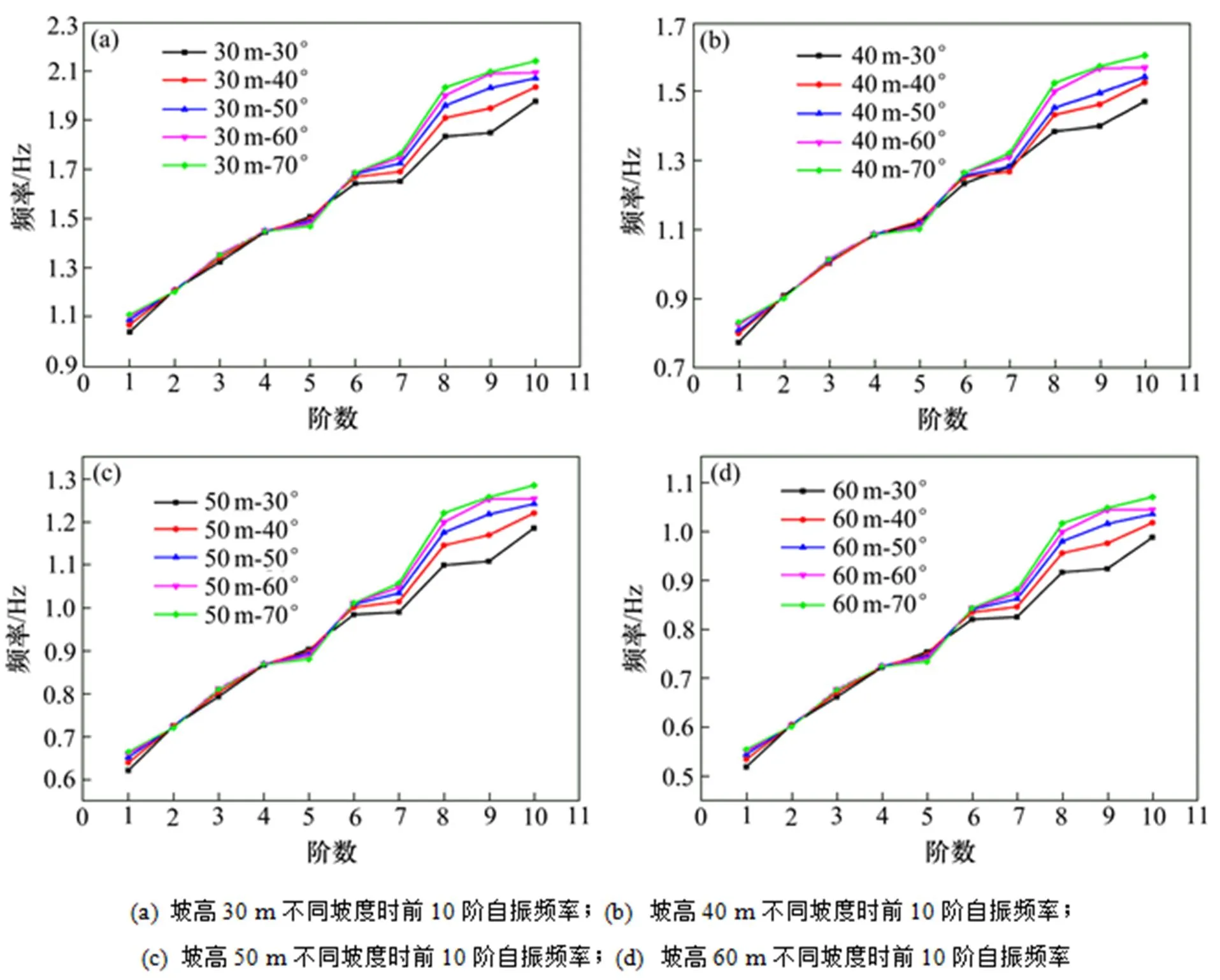
图2 各个坡高不同坡度时前10阶自振频率变化趋势

从图2可以看出，坡高分别为30，40，50和60 m时，各坡高的前10阶自振频率随坡度的增大而增大，但增加的幅度并不大。30 m坡高各坡度下的前10阶频率最大，60 m坡高时各坡度下的前10阶频率最小，即坡高越小，频率越大，坡高越大，频率越小。这是因为坡高和坡度越小，体系的质量越小，刚度越大，因此固有频率较大。各个坡高下，坡度分别为30°，40°，50°，60°和70°时，第2，3，4和5阶频率的变化不大，从第6阶频率开始，不同坡度各阶自振频率随阶数的增大变化比较明显，但总体来看，变化趋势相一致，坡度对自振频率的影响相对较小。

3.2 坡高对黄土边坡自振特性的影响

同样，对同一坡度下不同坡高时的黄土边坡的前十阶自振频率进行分析，其变化规律如图3 所示。

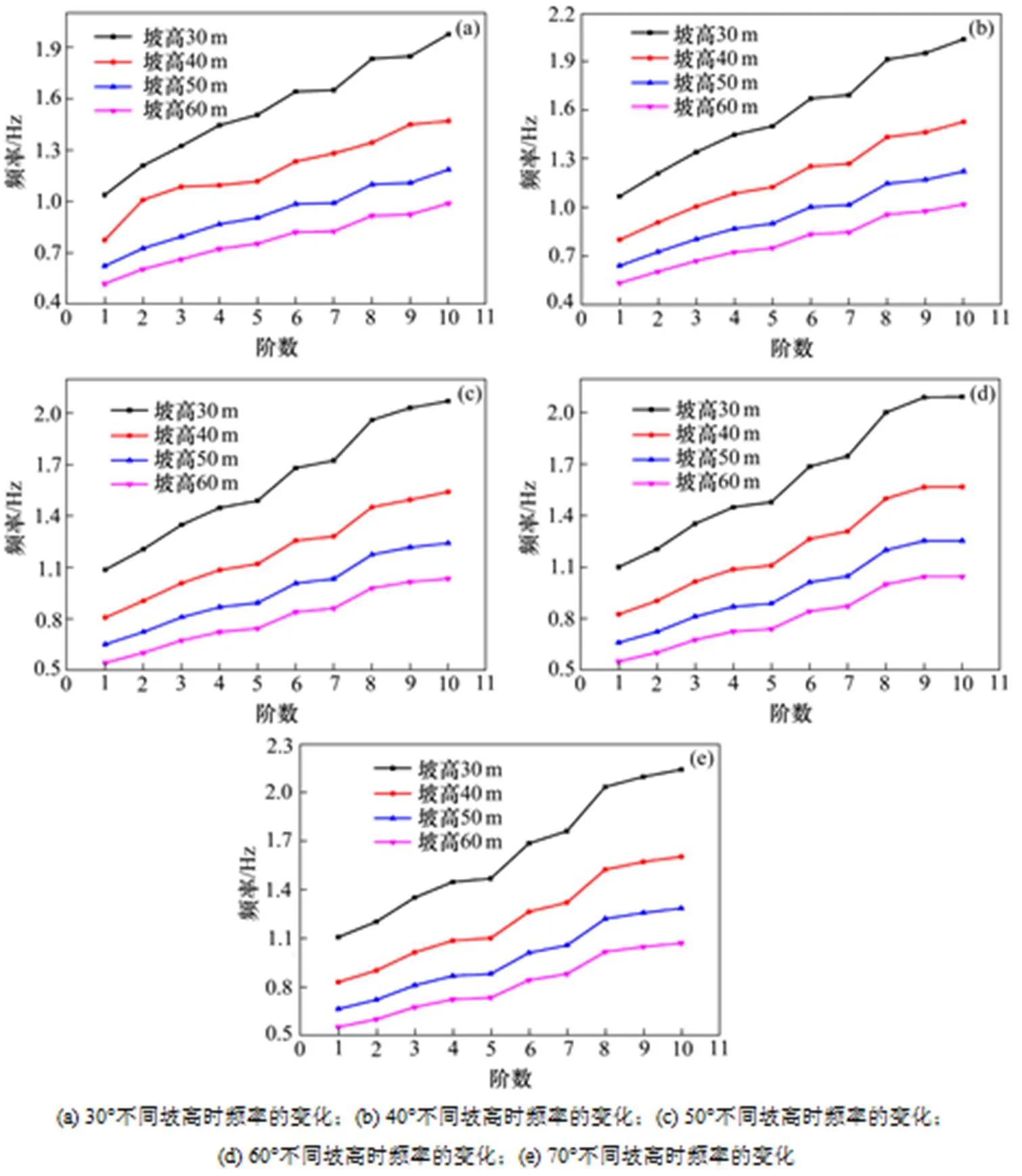
图3 各个坡度和不同坡高时前10阶自振频率变化

从图3可以看出，坡高对各阶自振频率的影响较大，同一坡度下，随着坡高的增大各阶自振频率明显下降且变化趋势一致，不同坡度时30 m高的黄土边坡自振频率最大，随着坡度的增大，黄土边坡的自振频率在降低，其中坡高为60 m坡度为30°时的边坡自振频率最小，坡高为30 m坡度为70°时的边坡自振频率最大；同一坡度不同坡高下各阶自振频率随频率阶数的增大而增大。

当地震波在岩土体中传播时，岩土体对地震波具有滤波和选择放大作用，当地震波的卓越周期与边坡的固有频率相接近时，边坡将发生共振而使边坡的动力响应放大。由以上对黄土边坡自振特性分析可以得知，坡度较大的矮黄土边坡对短周期地震波的放大作用可能较明显，而坡度较小且坡高较大的黄土边坡将对长周期波较为敏感，在地震中可能发生共振而使黄土边坡的动力响应放大，因此，在进行黄土边坡抗震设计时要加以注意。

3.3 坡高和坡度对基频的影响

言志信等[10]通过谐响应分析研究发现，只有前三阶固有频率被激发时才会产生强烈的振动现象，而第一阶固有频率处的共振为水平向振动，幅值最大，造成的危害也最大，其余两阶频率处共振幅值较小，对边坡造成的危害也较小。当地震动的频率与岩土边坡的固有频率接近时，边坡岩土体振动强度最强，即产生共振现象，这是造成边坡地震破坏的一个重要因素。因此，对不同坡高和坡度下的黄土边坡的基频变化规律进行了研究，如图4和图5所示。

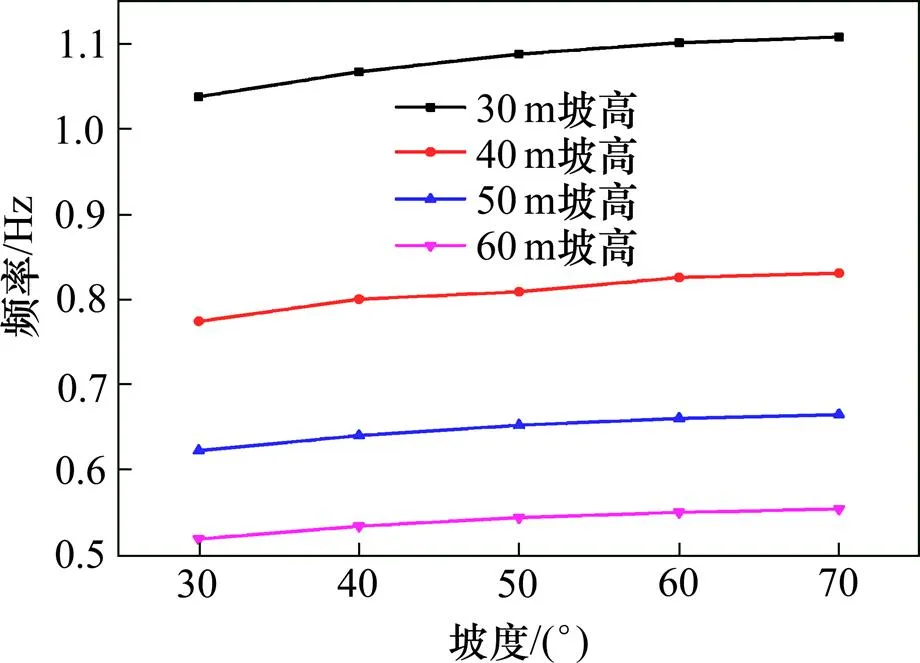
图4 不同坡高下基频随坡度变化

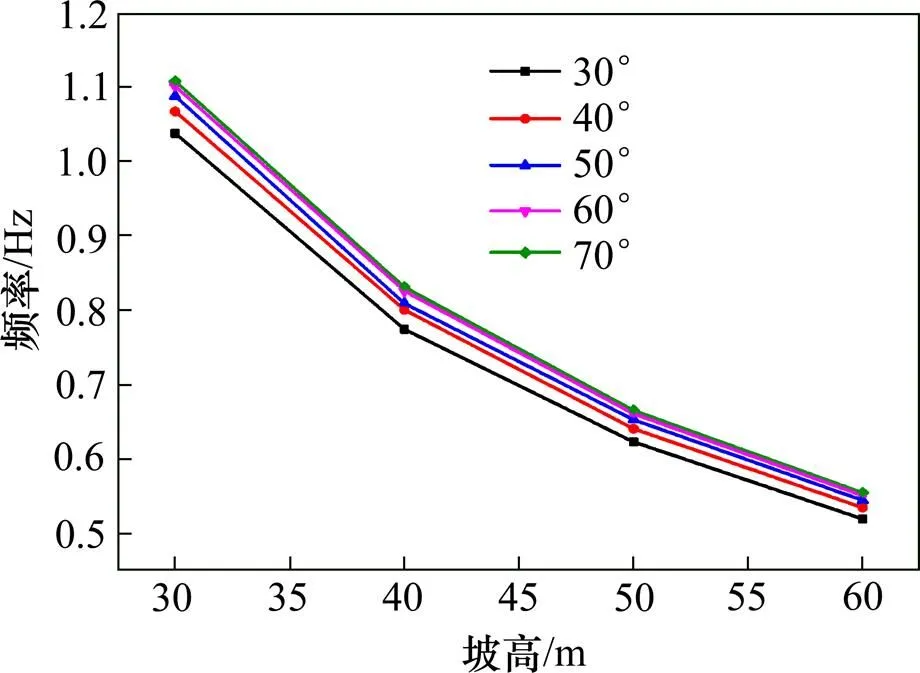
图5 不同坡度下基频随坡高的变化

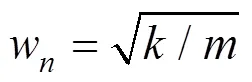
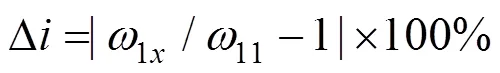
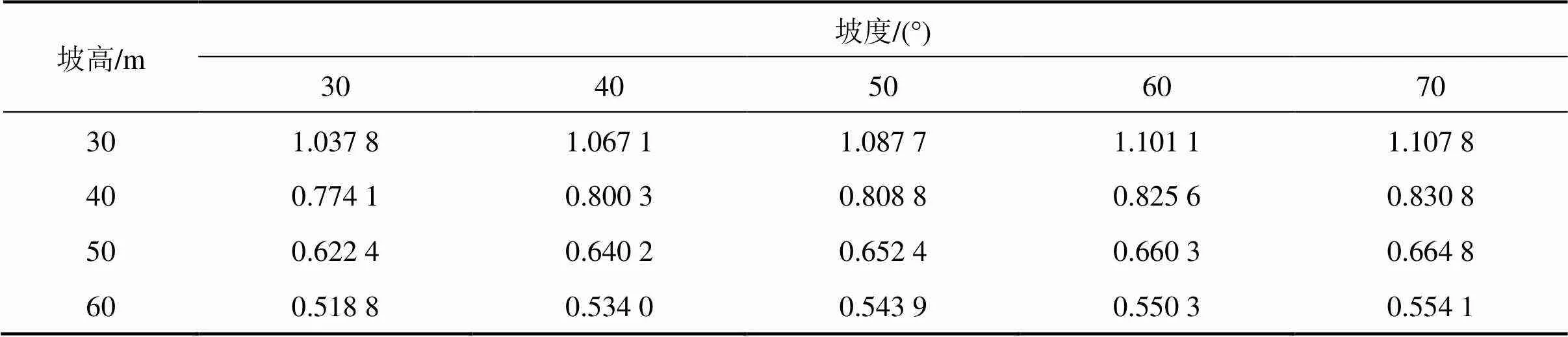
表2 不同坡高和不同坡度条件下边坡的基频

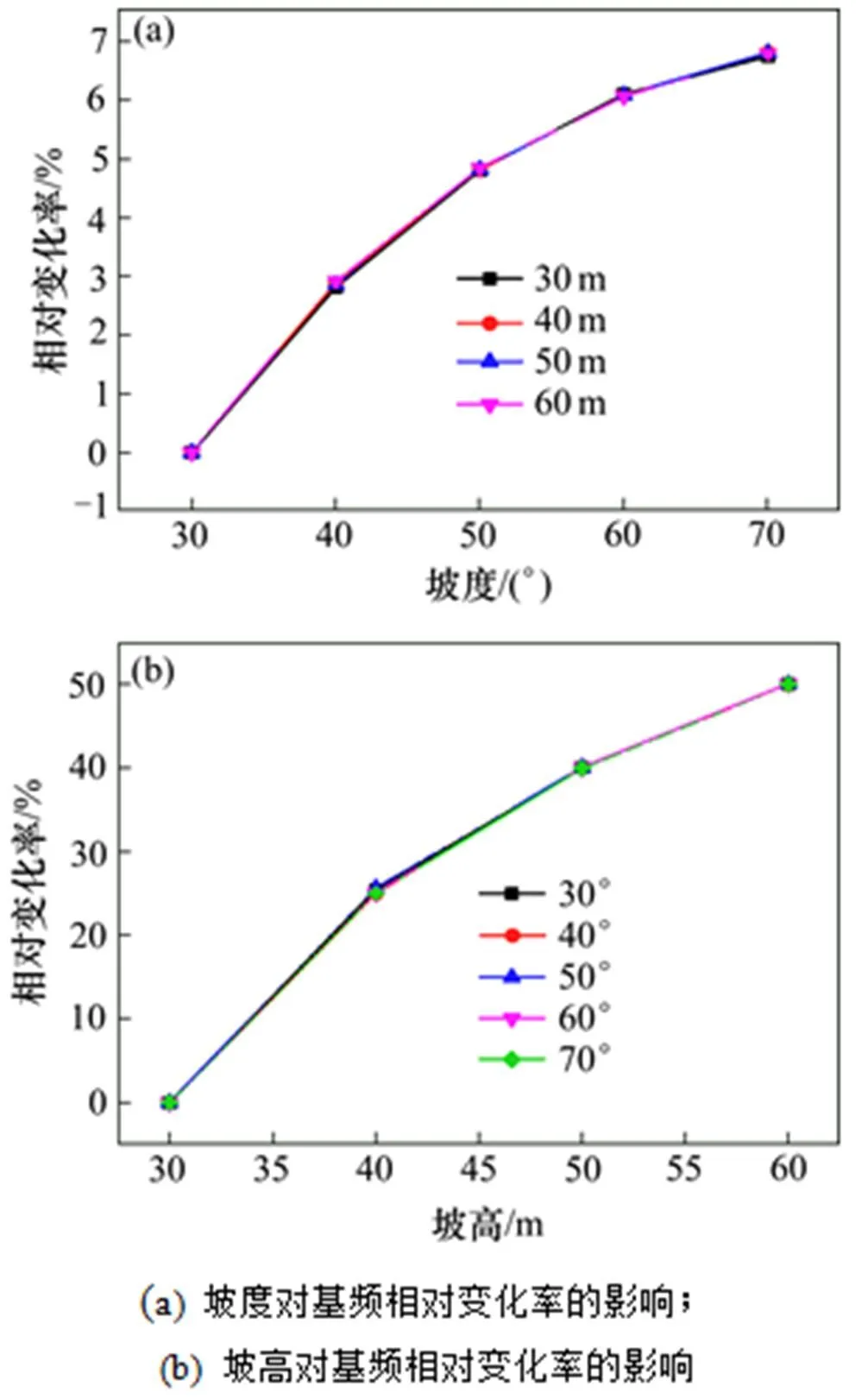
图6 坡度和坡高对基频相对变化率的影响

从图6可以看出，随着坡度和坡高的增大，基频的相对变化率均在增大，但坡度对基频相对变化率的影响较小，而坡高对基频相对变化率的影响较大。同一坡高不同坡度时基频的相对变化率的最大值为6.80%，是70°坡基频相对于30°坡基频的相对变化率，而且不同坡高时基频相对变化率随坡度变化的基本相同，其变化范围是6.74%~6.80%；同一坡度不同坡高时基频的相对变化率最大值为50.02%，基频随坡高的增大而减小，且减小幅度较大，相同坡度不同坡高时基频相对变化率的范围是49.95%~50.02%，是随着坡高的增大而降低的，由此更进一步说明了坡度对黄土边坡基频的影响 很小。

4 结论

1) 各坡高坡度条件下，黄土边坡的前10阶自振频率随频率阶数的增大而增大，同一坡高不同坡度时各阶自振频率随坡度的增大也有所增大，但增加幅度不大；各个坡高下，不同坡度时的第2，3，4和5阶频率变化不明显，从第6阶频率开始，不同坡度下各阶自振频率随阶数的增大变化比较明显，但总体来看，坡度对各阶自振频率的影响相对较小。

2) 坡高对各阶自振频率的影响较大，同一坡度下，随着坡高的增大各阶自振频率明显下降且变化趋势一致，坡高越小坡度越大时自振频率越大，坡高越大坡度越小时自振频率越小。

3) 随着坡度的增大，基频呈增大趋势，但坡度对基频变化的影响较小，同一坡高不同坡度时基频的相对变化率的最大值为6.80%；坡高对基频的影响较大，随着坡高的增大基频呈减小趋势，相同坡度不同坡高时基频相对变化率的范围是49.95%~ 50.02%。

4) 坡度较大的矮黄土边坡对短周期地震波的放大作用可能较明显，而坡度较小坡高较大的黄土边坡将对长周期地震波较为敏感，在地震中可能发生共振而使黄土边坡的动力响应放大，因此，在进行黄土边坡抗震设计时应加以注意。

[1] 王兰民, 孙军杰. 黄土高原城镇建设中的地震安全问题[J]. 地震工程与工程振动, 2014(4): 115−122.

WANG Lanmin, SUN Junjie. Seismic safety issues in the process of urban development in loess plateau[J]. Earthquake Engineering and Engineering Dynamics, 2014(4):115−122.

[2] 徐张建, 林在贯, 张茂省. 中国黄土与黄土滑坡[J]. 岩石力学与工程学报, 2007, 26(7): 1297−1312.

XU Zhangjian, LIN Zaiguan, ZHANG Maosheng. Loess in China and loess landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1297−1312.

[3] 陈国兴, 庄海洋, 杜修力, 等. 土−地铁隧道动力相互作用的大型振动台试验试验结果分析[J]. 地震工程与工程振动, 2007, 27(1): 164−170.

CHEN Guoxing, ZHUANG Haiyang, DU Xiuli, et al. A large-scale shaking tab le test for dynamic soil-metro tunnel interaction: Analysis of test results[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(1): 164−170.

[4] 祁生文, 伍法权, 刘春玲, 等. 地震边坡稳定性的工程地质分析[J]. 岩石力学与工程学报, 2004, 23(16): 2792−2797.

QI Shengwen, WU Faquan, LIU Chunling, et al. Engineering geology analysis on stability of slope under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2792−2797.

[5] 言志信, 郭斌, 张学东, 等. 黄土边坡动力响应分析[J]. 防灾减灾工程学报, 2012(5): 629−635.

YAN Zhixin, GUO Bin, ZHANG Xuedong, et al. Dynamic response analysis of loess slope[J]. Journal of Disaster Prevention and Mitigation Engineering, 2012(5): 629−635.

[6] 邓龙胜, 范文. 黄土边坡动力响应的影响效应研究[J]. 工程地质学报, 2012, 20(4): 483−490.

DENG Longsheng, FAN Wen. Research on dynamic response effects of loess slop[J]. Journal of Engineering Geology, 2012, 20(4): 483−490.

[7] 言志信, 曹小红, 张刘平, 等. 地震作用下黄土边坡动力响应数值分析[J]. 岩土力学, 2011(增2): 610−614.

YAN Zhixin, CAO Xiaohong, ZHANG Liuping, et al. Numerical analysis of loess slope dynamic response under earthquake[J]. Rock and Soil Mechanics, 2011(Suppl 2): 610−614.

[8] 吴志坚, 雷天, 陈豫津, 等. 黄土斜坡变形失稳破坏特征的振动台模型试验[J]. 上海交通大学学报, 2015, 49(7): 940−945.

WU Zhijian, LEI Tian, CHEN Yujin, et al. Deformation and instability characteristics of loess slope based on shaking table model test[J]. Journal of Shanghai Jiaotong University, 2015, 49(7):940−945.

[9] 张泽林, 吴树仁, 王涛, 等. 地震作用下黄土−泥岩边坡动力响应及破坏特征离心机振动台试验研究[J]. 岩石力学与工程学报, 2016(9): 1844−1853.

ZHANG Zelin, WU Shuren, WANG Tao, et al. Centrifugal shaking table test on dynamic response and failure characteristics of loess-mudstone slopes under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(9): 1844−1853.

[10] 言志信, 张学东, 张森, 等. 基于双向地震作用下边坡共振特性与固有频率研究[J]. 水文地质工程地质, 2011, 38(2): 46−51.

YAN Zhixin, ZHANG Xuedong, ZHANG Sen, et al. Study on resonance characteristics and natural frequency of slope under bi-directional seismic action[J]. Hydrogeology & Engineering Geology, 2011, 38(2): 46− 51.

[11] 言志信, 张学东, 张森, 等. 地震作用下边坡的共振响应研究[J]. 工程抗震与加固改造, 2011, 33(1): 6−11.

YAN Zhixin, ZHANG Xuedong, ZHANG Sen, et al. Study on seismic resonance effect of slope[J]. Earthquake Resistant Engineering and Retrofitting, 2011, 33(1): 6−11.

[12] 张学东, 言志信, 张森. ANSYS在岩质边坡动力响应分析中的应用[J]. 地震工程学报, 2010, 32(2): 117−121.

ZHANG Xuedong, YAN Zhixin, ZHANG Sen. numerical analysis on dynamic response of rock slope using ANSYS software[J]. Northwestern Seismological Journal, 2010, 32(2): 117−121.

[13] 杨巨文,白润才, 于永江, 等. 含弱层岩质边坡自振周期反演试验及数值验证[J]. 煤炭学报, 2015, 40(增): 69−75.

YANG Juwen, BAI Runcai, YU Yongjiang, et al. Inversion test and numerical verification on natural period of rock slope with weak layers[J]. Journal of China Coal Society, 2015, 40(Suppl): 69−75.

[14] 张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 2003, 34(1): 21−26.

ZHANG Luyu , ZHENG Yingren , ZHAO Shangyi, et al. The feasibility study of strength-reduction method with FEM[J]. Journal of Hydraulic Engineering, 2003, 34(1): 21−26.

[15] LIANG Qingguo, WU Xuyang, LI Chunqing, et al. Mechanical analysis using the unconfined penetration test on the tensile strength of Q3 loess around Lanzhou city, China[J]. Engineering Geology, 2014(183): 324−329.

[16] 王新敏. ANSYS结构动力分析与应用[M]. 北京: 人民交通出版社, 2014.

WANG Xinmin. Structural dynamic analysis and application with ANSYS[M]. Beijing: China Communications Press, 2014.

Analysis of influence factors on natural vibration characteristics of loess slope

SUN Weiyu1, 2, YAN Songhong1, 3, OU Erfeng1, 2, SONG Xuhui1, 2

(1. Key Laboratory of Road & Bridge and Underground Engineering of Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 3. Engineering Laboratory of Mechenics Application of Railway Transportation of Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China)

The dynamic characteristics of the slope are the internal factors that affect the dynamic response and play an important role in the dynamic stability of the slope. In this paper, used ANSYS large-scale general finite element analysis software, conducted modal analysis for different slope height and gradient of loess slope, discussed the influence of height and gradient for loess slope natural vibration frequency. The results showed that: under the condition of slopes with different height and gradient, the first 10 order natural vibration frequency of loess slope increased as the frequency orders increased. The influence of slope gradient for every order natural vibration frequency issmall relatively and slope height is large. With the increase of slope gradient, the fundamental frequency has an increase, but the increase is not large. Under the same slope gradient and different height, the maximum value of the relative change rate of fundamental frequency is only 6.80%. Slope height has a large influence for fundamental frequency, it will decrease with the slope height increase.The relative change rate of fundamental frequency is 49.95%~50.02% in the same slope gradient and different slope height. The research can provide reference for avoiding the occurrence of resonance in the seismic design of loess slope.

loess slope; self vibration characteristics; modal analysis; ANSYS

TU444

A

1672 − 7029(2018)01 − 0064− 07

2016−12−25

国家自然科学基金资助项目(51268030)；甘肃省科技计划资助项目(1310RJZA041)

严松宏(1966−)，男，江苏海安人，教授，博士，从事岩土与地下工程方面的教学与研究；E−mail：yansonghong@163.com