高斯光束参数简介及束腰的快速测量计算

崔立夫，罗瑞芳

(中国电子科技集团公司第四十六研究所 天津300220)

0 引 言

激光器是重要的光源，其光源的特性，如腰斑、束角、束宽、能量密度、脉宽等参数，对光纤传能的应用，如激光打标、起爆光纤等有着很大的影响。光纤系统中使用的激光光源其输出一般近似做高斯光束处理。本文从高斯激光束强度的角度出发，简要介绍了与高斯光束有关的实用概念，如高斯光束的束宽、瑞利距离、共焦参数、“M2”值、光强分布、光斑的有效面积及能量密度等，并介绍了一种快速测量高斯光束腰斑尺寸的方法——90/10刀口法，与孔径法、CCD扫描法、曲线拟合法等其他测量方法相比更快速、更简便、更精确。高斯光束腰斑尺寸的精确测量对与之相关的应用，如光斑的有效面积、光束质量因子的判定等有着重要的意义。

1 光斑强度分布

光源通常产生的是非均匀的光束，其强度在横截面上的分布与其模数有关，图1和图2分别介绍了几种低阶埃尔米特-高斯函数和几种低阶埃尔米特-高斯光束的截面光强分布图。

在光纤系统中使用的光源，一般近似选用 LP01模式，其横向分布呈现高斯分布，是我们熟悉的钟形曲线分布，如图 1(a)所示，其光斑分布如图 2(a)。多数的气体激光器及经特殊设计的激光发光管都是此类分布。

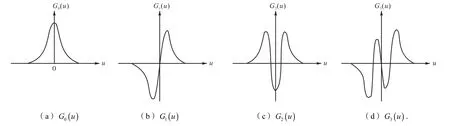
图1 几种低阶埃尔米特-高斯函数Fig.1 Several low-order Hermite-Gaussian functions

图2 几种低阶的埃尔米特-高斯光束的截面光强分布图。Fig.2 Intensity distributions of several low-order Hermite-Gaussian beams in the transverse plane

1.1 高斯光束光强分布

在传能的应用中，其效能都直接与光的强度有关，从光强的角度而不是从电磁波振幅的角度来讨论，可使概念清晰化，对应用而言并无影响。

高斯光束的光强分布可用下式表示：

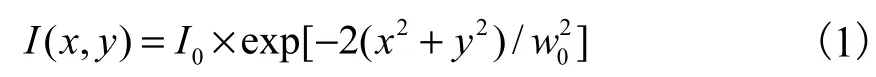
式中I0表示最大峰值强度，w0为最高峰值强度下降到时光斑半径。高斯光束经透镜聚焦后，其焦面上的强度分布仍为高斯分布，但强度有所降低，其斑点尺寸：

高斯光束经聚焦后，绝大部分能量(86.5%)都被“封闭”在以为直径的圆域内称为斑点直径。

1.2 高斯光束光强分布式的归一化

因高斯光束是轴对称分布的，式(1)经参量变换后，可得：为数学上处理简单起见，将式(3)作归一化处理，即

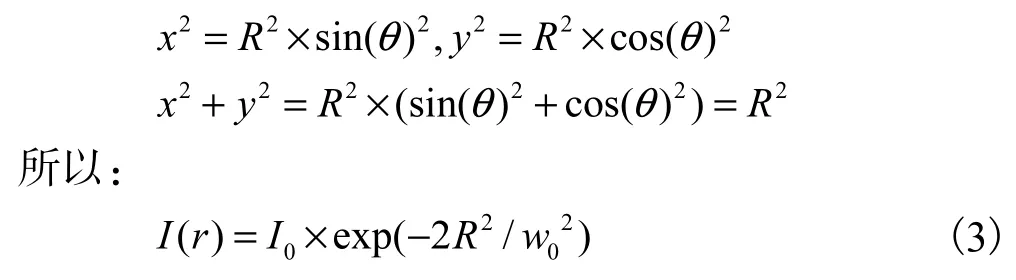
式(3)变为：

光斑的总能量P既为曲线(4)绕纵轴旋转体的体积，或是曲面(3)在圆域(r)的积分：

图3 高斯光束的强度分布(归一化)Fig.3 Normalized intensity distribution of Gaussian beam

图 3和图 4分别为高斯光束归一化处理后的二维和三维强度分布图，其中三维图形象化地展现了能量密度的分布，等高图则近似为实际的能量分布。

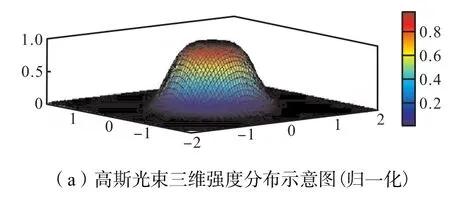
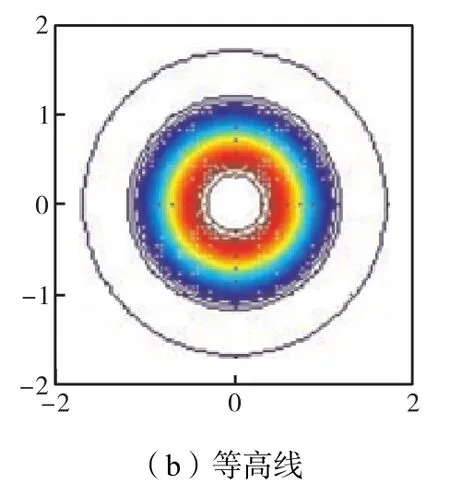
图4 高斯光束三维强度分布示意图(归一化)及其等高线图Fig.4 Three-dimensional diagram of normalized Gaussian beam intensity distribution and the contour

2 高斯光束参数介绍

2.1 高斯光束的束宽、瑞利距离和共焦参数

由激光物理可知，高斯光束呈双曲线函数发散，如图5所示。

这里z=0定义为束腰w0的位置，被称为瑞利距离，与束腰轴向距离等于瑞利距离zR处的束宽为这两点间的距离称为“共焦参数”

图5 高斯光束参数关系示意图[2]Fig.5 Parameter relationships of Gaussian beam[2]

由式(6)可得出，波长为λ的高斯光波的腰斑位置在Z轴上的分布为：

其光束的偏移既扩散角为：

由式(8)可知，较小的w0其发散角则较大，应用时应予以注意。

2.2 高斯光束的“M2”值

激光束的质量可以用束参数乘积(BPP)来衡量，BPP的数值就是光束的偏移量与束腰w0的积。实际光束的 BPP与理想光束的比值称为“M,2”，高斯光束的 M,2＝1。实际光源的“M,2”都大于 1，M,2越接近1表明此光束越近似于高斯光束。

2.3 高斯光束的能量分布

从高斯光束的能量分布图来看，中心的光强度最大(r=0)，随后以负指数下降，可用下式表示：

从式(5)可知，光强的峰值I0与总能量的关系为平均能量的 2倍，平均能量等于总能量除以半径为的圆面积：

2.4 高斯光束光斑的有效面积及能量密度

实际激光能量的分布是非均匀的，激光器由于调制的原因，会有多个峰值，并且存在一个最大的峰值。在这个最大峰值能量密度下，光学材料(光纤)最易受损伤，即对传能光纤而言有一个损伤阀值(等离子点火)。

由于调制激光器输出能量有多峰性，计算时往往取其最大峰值能量。对于连续工作激光器，其功率用瓦(W)来表示，而脉冲激光器用焦耳/秒表示。如10,mJ输出，脉宽 10,ns，则输出的峰值功率为10(mJ)/10(ns)＝100,MW。

高斯光束光斑的有效面积(Aeff)定义如下：高斯光束的能量密度定义：激光的总能量除以光斑的有效面积就等于光斑的能量密度。

如果光束(100,MW)聚焦在束腰半径w0=200,μm的腰斑上，则其光斑的能量密度为：所谓光损伤阀值是指激光与光学材料(如光纤)相互作用后不产生损伤的最大允许的激光能量密度。

3 高斯光束腰斑的快速测量及计算

3.1 测量方法

无论用何种方法(孔径法、CCD扫描法)测量高斯的光强分布及其后的拟合计算都冗长、耗时。采用曲线拟合的方法要求测量点数要尽量多，若用内插或外插的数据虽可增加拟合的数据点数，但因精度的问题拟合得出的数据准确度差。这里介绍一种快速确定腰斑尺寸的方法——刀口法，因其测量 90%及10%的透过光强，又称 90/10刀口法，其测量示意图和刀口切割光束示意图如图6所示。

此方法的特点是利用高斯光束的数学特征，转换成以误差函数来表征的高斯分布，只需测量特定点的光强，经简单的计算即可求出光束的腰斑尺寸。

图6 刀口法测量示意图Fig.6 The blade measurement method

3.2 理论计算方法

将式(3)，重写为下列形式：

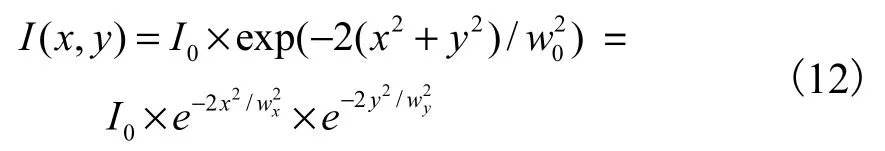
其中，xω和yω分别为光束在x及y方向的半径，I0为峰值强度。光束中的总能量Ptot为上式的积分：

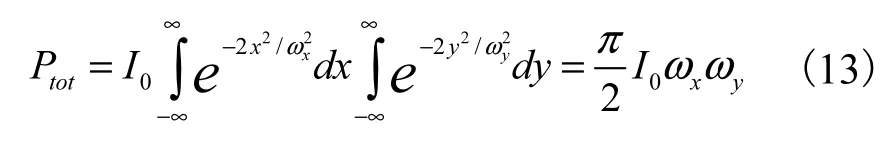
在刀口法中，一般只测x方向上的能量，则：

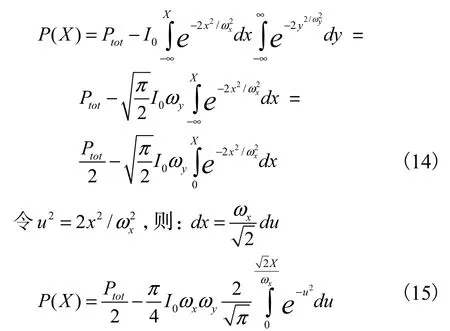
方差＝1/2的高斯分布的二倍积分。)对比方程(14)的表达式可知：

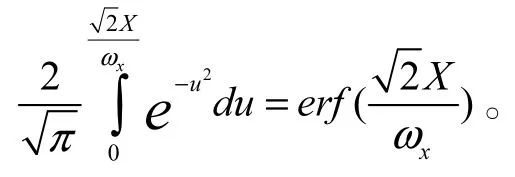
所以，光束在x方向的能量(以误差函数形式)的表达式为：

以误差函数表示的高斯分布函数，为高斯概率密度函数的积分，如下式：

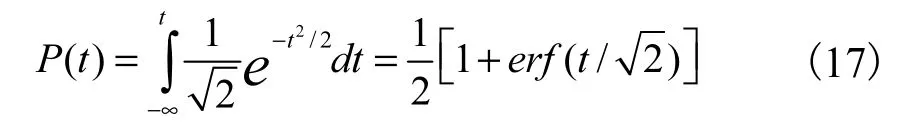
测量 10%,的功率对应的X并记为X10，代入(16)中，得：

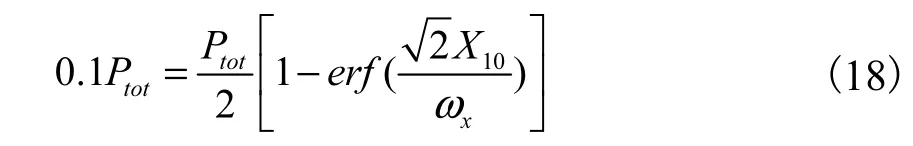
整理后为：

带下标的ω表示是经由x方向测得的光束腰斑的半径。

采用刀口法，理论上任何的功率透过率的比值[P%,/(1-P%,)]都存在有的等式(A为常数，但并不相同)。为了便于应用，计算了各种功率比值的比值表，使用中测出P%,/(1-P)%,的X方向的差值ΔX ，再选取所对应的A代入(20)，即可得到高斯光束的腰斑半径(见表1)。

表1 P,%/(1-P)%和对应的A值Tab.1 P,%/(1-P)%, and the corresponding A values

误差分析表明，采用 90%/10%法，因其使用了误差函数最大变化区域的端点，故其误差最小。为保证测量的准确性，一般采用多次测量，再取平均值的方法以消除测量误差。

4 结 论

本文从高斯激光束强度的角度出发，简要地介绍了高斯光束的概念及相关参数，如高斯光束的束宽、瑞利距离、共焦参数、“M,2”值、光强分布、光斑的有效面积及能量密度等，并介绍了一种测量高斯光束腰斑尺寸的新方法——90/10刀口法。能够更加快速、精确地测量高斯光束的腰斑尺寸，这对与之相关的应用如光斑的有效面积、光束质量因子的判定等有着重要意义。

［1］ Palais J C. Fiber Optic Communications[M]. 5版. 北京：电子工业出版社，2009.

［2］ Mathews J H. Numerical Methods Using MATLAB[M]. 3版. 北京：电子工业出版社，2002.

［3］ 张忠占. 统计学方法与数据分析引论[M]. 5版. 北京：科学出版社，2003.