基于EEMD和CICA的风电机组轴承故障特征提取

许崇新，徐樊浩

（国网山东省电力公司烟台供电公司，山东 烟台 264001）

0 引言

作为一种具有大规模应用的清洁能源，风能发电在电网渗透率日益增高。风电机组作为风能发电的核心设备，保证其安全稳定运行显得至关重要。而风电机组运行环境相对恶劣，且安装位置高，不便于检修。为此，研究人员开展了一系列有关风电机组的状态监测研究工作，尽早发现故障，避免事故扩大［1］。风电机组多个部位装配有轴承，诸如主轴、齿轮箱等，轴承故障在风电机组故障中所占比例很高［2］。

振动信号分析方法是轴承等机械设备状态监测与故障诊断的主要方法之一。目前，快速傅里叶变换FFT（Fast Fourier Transform）［3］、小波变换［4］、经验模态分解［5-6］（Empirical Mode Decomposition，EMD）等方法常被用来分析轴承等机械设备的振动信号。但是这些方法存在一定的缺陷，诸如FFT只适合处理平稳信号、小波变换中小波基的选取对结果影响较大、经验模态分解存在模态混叠等。为解决模态混叠问题，Huang等人提出的EEMD方法在需要分解的信号中引入白噪声，不但可以抑制EMD方法中存在的模态混叠问题，而且可以将需要分解的信号与白噪声当作一个整体进行EMD分解。因此，利用EEMD方法对测得的风电机组轴承故障振动信号进行自适应分解，并选取能体现轴承故障特征的本征模函数（Intrinsic Mode Function，IMF），对于提取轴承故障振动信号特征具有重要价值［7］。此外，这些方法均是直接分析测得的变压器振动混合信号，得到的信号特征成分比较复杂，不易于辨识具体的异常状况。

基于参考信号的独立分量分析方法（Constrained Independent Component Analysis，CICA） 是在独立分量分析（Independent Component Analysis，ICA）的基础上发展而来，近年来普遍应用在生物医疗、图像以及语音信号处理等问题上。其应用先验知识建立能够表征目标信号时间特性的参考信号，将其引入基于参考信号的独立分量分析运算中，形成某种约束限制算法的收敛方向，从而可以从多异常混合信号中得到目标异常的特征信息。文献［8］采用CICA方法从人脸图像和功能磁共振数据中提取了有效特征信息；文献［9］利用感兴趣信号的周期特性，建立脉冲参考信号，从而采用CICA方法分离出轴承故障信号。但是在实际应用中，有些时候轴承的先验知识不容易确定，并不能建立较好的参考信号，从而限制了该方法的应用。

为解决上述问题，提出基于EEMD和CICA的风电机组轴承故障特征提取方法对风电机组轴承故障振动信号进行分析。根据EEMD方法分解信号的特点，并结合信号独立性要求，建立参考信号。然后利用CICA方法提取轴承故障中包含的信号特征，并进行包络解调得到包络谱。分析实测实验数据表明，该方法不仅能够实现信号特征提取，而且可以实现故障与正常振动信号特征的分离。

1 风电机组轴承故障振动信号EEMD

风电机组轴承故障振动信号EEMD方法具体步骤为：

1）初始化EMD次数N，选择加入白噪声的幅值系数k。

2）向测得的轴承故障振动信号x（t）中加入 N次均值为0，幅值系数为k的高斯白噪声序列ni（t）（i=1，2，…，N），即

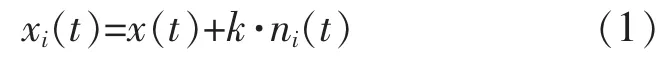
3）对得到的xi（t）分别进行 EMD 分解，得到各个IMF分量和残余项，即

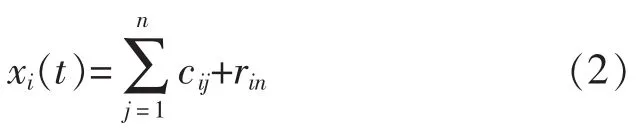
式中：cij为第 i次引入高斯白噪声信号后，对 xi（t）进行分解得到的第j个IMF分量；rin为第i次加入高斯白噪声后，对xi（t）进行分解后的余项；n为分解层数。

4）将通过上述步骤得到的IMF分量进行总体平均运算，抵消引入高斯白噪声信号所带来的影响，最终得到EEMD方法对应的IMF分量为

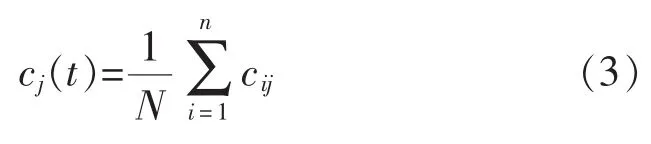
式中：cj（t）为EEMD方法分解轴承故障振动信号后所得到的第j个IMF分量。

2 风电机组轴承振动信号特征提取

2.1 CICA算法

CICA算法的基本模型为［10］

目标函数：

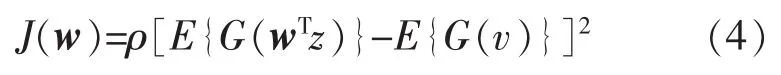
约束条件：

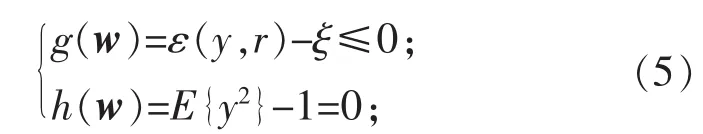
式中：ρ为正常量；w为使目标函数极大的估计系数矩阵；E｛·｝为期望值；z为输入信号；y=wTz为输出信号；r为参考信号；v为零均值、单位方差的高斯变量；G（·）为任意一个非二次方程；g（w）为相似性测度参数；ξ为阈值参数；ε（y，r）为源估计 y 和 r之间的广义距离函数；h（w）为独立分量等式约束。根据高斯性的不同，G（·）可以取以下函数：

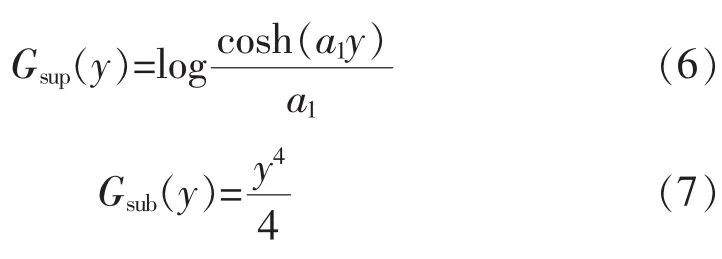
式中：1≤a1≤2，a2≈1。 根据 y和 r的差异程度的不同，可以选择或者ε（y，r）=-（E｛（yr）｝）。 ξ是门限，用于区分目标信号与其他信号，其取值范围为

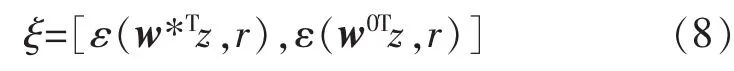
为了获得在条件式（5）约束下目标函数式（4）的最优解，首先建立拉格朗日函数

极大化拉格朗日函数式（9），即可获得单元CICA的Newton-like算法为

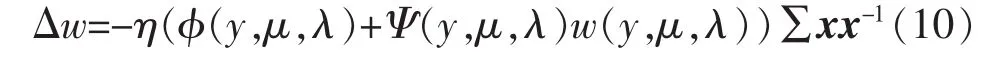
其中，

式中：G′y（y）、G″y（y）和 g′（w）、g″（w）分别为 Gy（y）、g（w）的一阶导数和二阶导数；μ、λ为拉格朗日因子，由以下迭代算法得到：

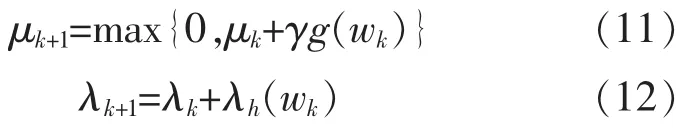
2.2 参考信号的选取

采用EEMD方法对轴承故障振动信号x（t）进行分解，得到若干 IMF 分量 ci（t）（i=1，2，…，d）及残余项。将及其IMF分量重新组合，得到一个虚拟的多通道传感器观测信号则虚拟信号xIMF（t）的协方差矩阵Rx可表示为

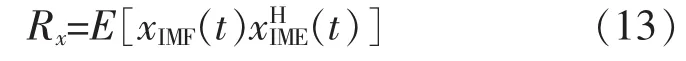
对协方差矩阵进行奇异值分解，可以有效消除轴承故障振动信号中包含的噪声成分，得到相对纯净的特征信号。协方差矩阵Rx的奇异值分解为

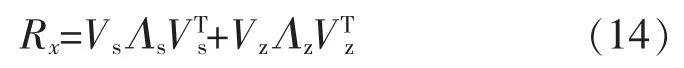
式中：Λs=diag｛λ1，…，λd｝表示为 d 个按照递减顺序排列的主特征值；ΛZ＝diag｛λd+1，…，λv｝表示为 v-d 个噪声特征值。

由于主特征值与噪声特征值之间阈值难以设定，因此采用邻近奇异值差值法对源信号数进行估计。其以协方差矩阵的奇异值分解为基础，计算得到邻近奇异值的差值统计量为

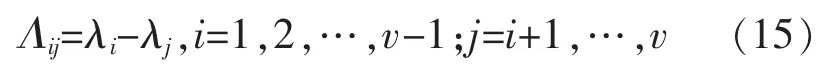
当 λi和 λj都是噪声奇异值时，Λij比较小；λi当和λj其中的一个或两个都是信号奇异值时，Λij比较大。从最小奇异值开始比较，相邻奇异值差值较大的分界处，就是轴承故障振动信号子空间和噪声子空间的分界面。从而估计出轴承故障振动源信号个数m。

由政府主导，行业协会指导，跨境电商领军型企业牵头，在共享供应链的基础上，以跨境物流联盟的形式共建海外仓。针对义乌跨境电商产业中跨境物流成本高的问题，一方面通过引导义乌中小跨境电商出口企业在共创品牌提升产品附加值的基础上提高海外仓的应用，加强海外仓物流信息的可视化和透明化，让卖家更好掌控物流、运营、财务等状况；另一方面需要加强规范化建设，主动为企业提供海外仓政策、法律、税收等咨询服务，提供融资、审批、资格认证等政策支持，可通过政府专项资金帮助义乌中小跨境电商出口企业体验海外仓带来的便利和业绩提升，提升义乌小商品的产品附加值和竞争力。

由于EEMD方法分析轴承故障振动信号x（t）所得IMF分量能体现源信号特征信息，若IMF分量统计独立性越高，则其能够体现源信号独立成分，越适合用于建立参考信号。由于互信息是衡量一组随机变量之间独立性的重要准则，因此将其当作IMF分量选取的准则。互信息值可以根据互累积量近似得到［11］，即

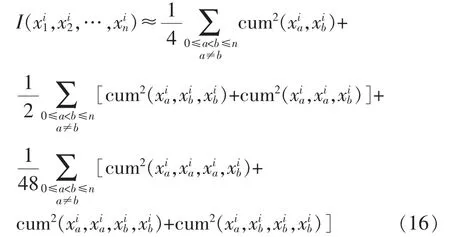
式中：cum（*，*）、cum（*，*，*）、cum（*，*，*，*）分别为xi（t）的二、三、四阶互累积量。

通过计算IMF分量的归一化互信息值，根据估计的源信号个数m，选取互信息值较小的m个IMF分量组成参考信号提取轴承故障振动信号特征。

2.3 信号特征提取步骤及效果评价

对测得的轴承故障振动信号进行去均值等预处理，削弱噪声信号的影响；利用EEMD对风电机组轴承故障振动信号x（t）进行分解，获得若干IMF分量；利用邻近奇异值差值法估算源信号的个数m；根据式（16）分别计算各个IMF分量的归一化互信息值，选取归一化互信息值最小的m个IMF分量建立参考信号；利用CICA方法提取轴承故障信号，并进行包络解调，得到轴承故障特征。

3 轴承故障实例分析

3.1 实例设计

本实例使用来源于Western Reserve University的轴承故障数据［12］。测试平台包括发电机、转矩传感器等设备，如图1所示。

图1 测试实验台

实验中，采样频率为12 000 Hz，轴承转速为1 749 r／min。轴承具体参数如表1所示。

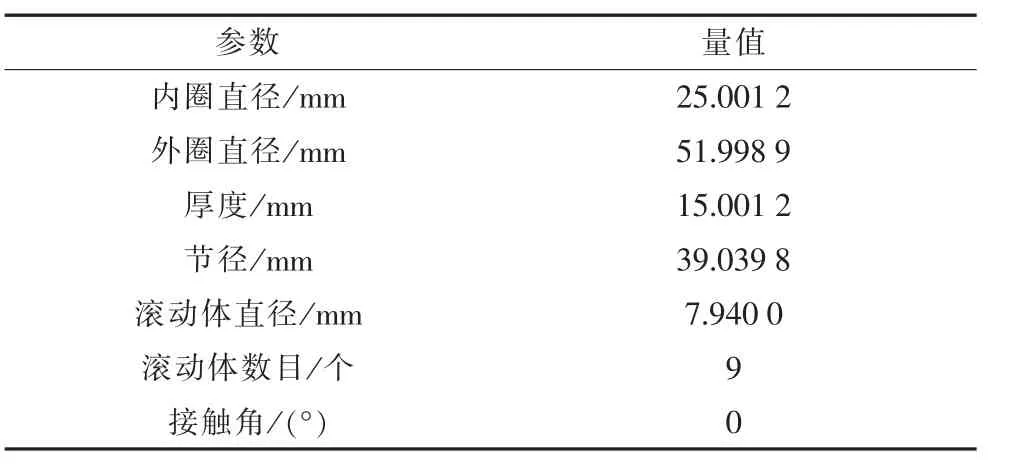
表1 轴承参数

计算轴承内外圈故障的公式为

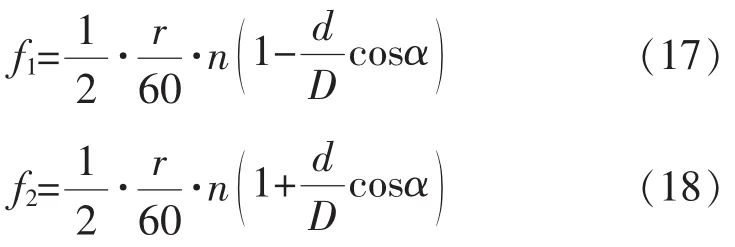
式中：f1、f2分别为内圈、外圈故障频率；r为转速；n为滚动体个数；d为滚动体直径；D为轴承节径；α为接触角角度。

进而，可得轴承正常与故障时特征频率，如表2。

表2 轴承特征频率 Hz

3.2 轴承外圈故障特征提取

主轴承外圈早期故障时，传感器采集振动信号，经取均值、去噪等预处理后，到的时域波形与频谱如图2所示。从图中虽然可以看出故障特征频率成

分，但幅值相对较小，不容易分辨。

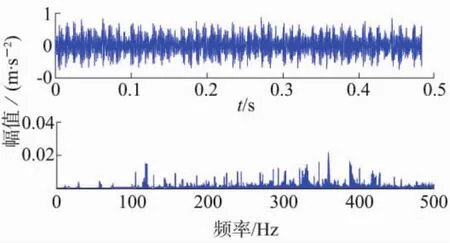
图2 主轴承外圈故障时域波形与频谱图

对测得的主轴承外圈故障信号x1（t）进行EEMD分解，得到 IMF 分量 c1（t），…，c10（t）以及残余分量r10（t）。 图 3 表示 x1（t）经分解后得到的前 7 阶 IMF分量图。

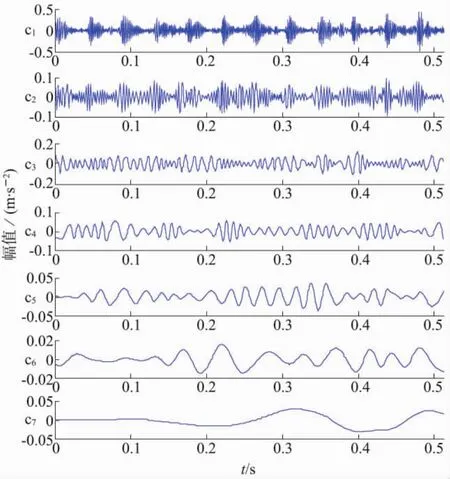
图 3 IMF 分量（c1～c7）

将故障信号x1（t）与得到的IMF分量组成新的多维信号 xIME（t）=（x1（t），c1（t），…，c10（t），r10（t）），并进一步计算对应的相关矩阵然后对Rx进行奇异值分解，得到特征值按照从大到小的顺序排列的矢量 Λ=diag｛λ1，…，λ12｝。 根据邻近奇异值差值法，计算相邻特征值之差，如图4所示，可知源信号个数为2个。

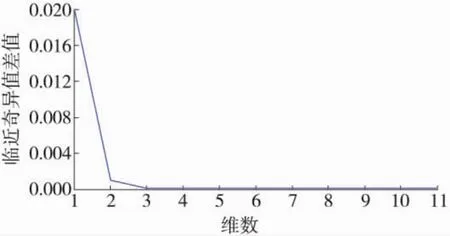
图4 多维信号奇异值差值分布

根据前文所述参考信号选取方法，选取归一化互信息值最小的前两IMF分量作为参考信号，提取故障数据中包含的故障特征，并进行包络解调，得到图5所示包络谱。

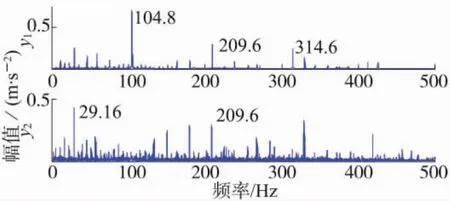
图5 轴承外圈故障提取信号包络谱

从图5可以看出，利用所述方法得到的信号包络谱中，在104.8 Hz频率成分及其二倍频、三倍频（209.6 Hz、314.6 Hz）位置处幅值明显较大，且与计算所得轴承外圈故障特征频率值及其倍频基本一致。据此，可以得知轴承外圈存在故障。同时，y2中还包含有轴承的旋转频率（29.16 Hz），说明所提方法同时也能够实现轴承故障与正常振动信号特征的分离。

3.3 轴承内圈故障特征提取

主轴承内圈故障时，传感器采集振动信号，图6为经预处理后轴承内圈故障时域波形及频谱，从图中也很难辨识出内圈故障特征频率。

图6 主轴承内圈故障时域波形与频谱

与轴承外圈故障特征提取类似，利用本文所提方法得到提取信号的包络谱，如图7所示。

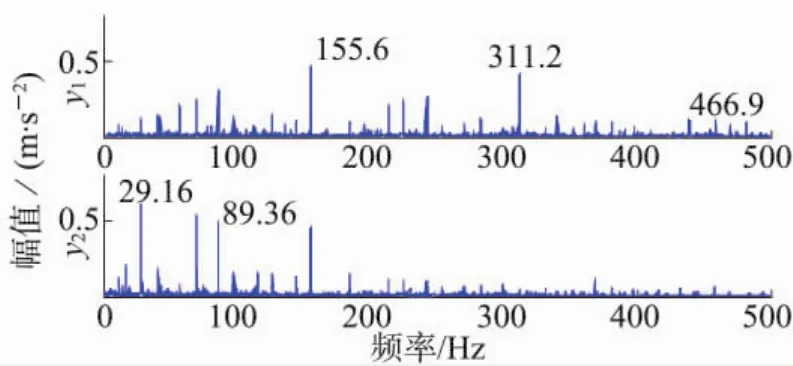
图7 轴承内圈故障提取信号包络谱

从图7可以看出，在155.6 Hz频率成分及其二倍频、三倍频（311.2 Hz、466.9 Hz）位置处幅值明显较大，且与计算所得轴承内圈故障特征频率值及其倍频基本一致。据此，可以得知轴承内圈存在故障。同时，轴承内圈故障提取信号y2中也还包含有轴承的旋转频率（29.16 Hz），以及三倍频，进一步验证所提方法的有效性。

4 结语

利用基于EEMD和CICA的风电机组轴承故障特征提取方法分别提取轴承外圈、内圈故障振动信号中包含的特征信息，并对提取信号进行包络解调，得到明显的轴承内、外圈故障特征频率成分。因此，所提方法可以有效突出轴承故障特征信息，实现对不同轴承故障特征的有效提取，有利于避免轴承故障的扩大。

［1］HAMEED Z，HONG Y S，CHO Y M，et al．Condition monitoring and fault detection of wind turbines and related algorithms：A review［J］．Renewable and Sustainable Energy Reviews，2009，13（1）：1-39．

［2］赵明浩．风力机故障特征分析与实验研究［D］．北京：清华大学，2010．

［3］BAFROUI HH，OHADI A.Application of wavelet energy and Shannon entropy for feature extraction in gearbox fault detection under varying speed conditions ［J］.Neurocomputing，2014，133（8）：437-445.

［4］严如强，钱宇宁，胡世杰，等．基于小波域平稳子空间分析的风力发电机齿轮箱故障诊断［J］．机械工程学报，2014，50（11）：9-16．

［5］郭艳平，颜文俊，包哲静，等．基于经验模态分解和散度指标的风力发电机滚动轴承故障诊断方法［J］．电力系统保护与控制，2012，40（17）：83－87，93．

［6］林近山．基于经验模式分解和谱峭度的滚动轴承故障诊断［J］．机械传动，2012，36（9）：76－79．

［7］胡爱军，马万里，唐贵基．基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法［J］．中国电机工程学报，2012，32（11）：106-111，153.

［8］LU W，RAJAPAKSE J C．Approach and applications of constrained ICA［J］.IEEE Transactions on Neural Networks，2005，16（1）：203．

［9］王志阳，陈进，肖文斌，等，基于约束独立成分分析的滚动轴承故障诊断［J］．振动与冲击，2012，31（9）：118－122．

［10］ WEI L，RAJAPAKSE JC．ICA with reference ［J］．Neurocomputing，2006，69（16-18）：2 244-2 257．

［11］ CARDOSO J F．Dependence，correlation and Gaussianity in independent component analysis［J］．Journal of Machine Learning Research，2003，4（4）：1 177-1 203．

［12］ Case Western Reserve University.Bearing data center［EB／OL］．http：／／csegroups.case.edu／bearingdatacenter／pages／，2013－07－15.