解析Besov型空间在Bloch空间的闭包

钱 睿 深

(岭南师范学院 数学与统计学院，广东 湛江 524048)

1 引 言

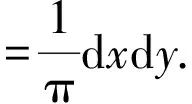
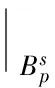
令Bloch空间B表示满足下列条件的全体函数f∈H(D)：

2 主要结果

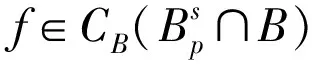
(1-|z|2)|f′(z)|≤(1-|z|2)|f′(z)-g′(z)|+(1-|z|2)|g′(z)|，

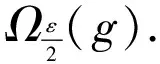
另一方面，设f∈B.由文献[11,引理4.2]知，

令

以及

那么f(z)=f1(z)+f2(z).现在将证明f1∈B.因为f2(z)=f(z)-f1(z)，所以

即f2∈B，其中，C为正常数.从而，易知f1∈B.

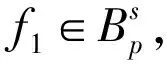
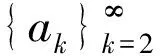
称θ(z)为Blaschke乘积.

所以对于任意的ε>0，可以推出

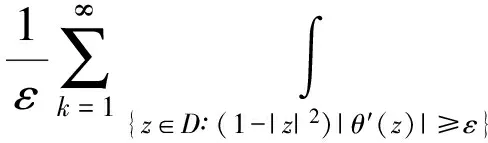
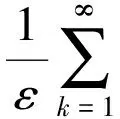
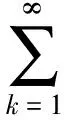
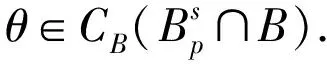
因此，

由文献[12,69页]，有

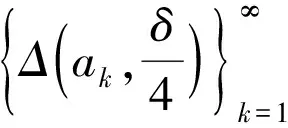
证毕.

[1] N. Arcozzi, D. Blasi and J. Pau, Interpolating sequences on analytic Besov type spaces[J].Indiana Univ Math J，2009，58：1281-1318.

[2] J Anderson, J Clunie ， Ch Pommerenke, On Bloch functions and normal functions[J]. J Reine Angew Math， 1974，270：12-37.

[3] D. Blasi and J. Pau, A characterization of Besov-type spaces and applications to Hankel-type operators[J]. Michigan Math J，2008，56： 401-417.

[4] L Carleson, An interpolation problem for bounded analytic functions[J]. Amer J Math，1958，80：921-930.

[5] L Carleson, On the zeros of functions with bounded Dirichlet integrals[J]. Math Z，1958，56：289-295.

[6] L Carleson, Interpolation by bounded analytic functions and the Corona problem[J]. Ann of Math，1962，76：547-559.

[7] P Galanopoulos, N. Monreal Galan and J. Pau, Closure of Hardy spaces in the Bloch space[J]. J Math Anal Appl.，2015，429：1214-1221.

[8] D Girela, J. A. Pelaez and D. Vukotic, Integrability of the derivative of a Blaschke product[J]. Proc Edinb Math Soc，2007，50：673-687.

[9] N Monreal Galan and A. Nicolau, The closure of the Hardy space in the Bloch norm[J]. Algebra i Analiz. 2010，22：75-81, translation in St. Petersburg Math J，2011，22：55-59.

[10] ZHAO R. Distances from Bloch functions to some Mobius invariant spaces[J]. Ann. Acad Sci Fenn Math,2008,33：303-313.

[11] ZHU K. Bloch type spaces of analytic functions[J]. Rocky Mountain J Math，1993，23：1143--1177.