考虑湿接缝刚度损伤的桥梁荷载横向分布计算方法

邬晓光，钱若霖，苏 佩

(长安大学 公路学院，陕西 西安 710064)

多梁式T梁或小箱梁结构形式在我国公路桥梁总数中所占比重较大。目前国内外对于这些桥的荷载横向分布系数的计算方法均假定桥梁的结构性能完好，如传统的偏心压力法，刚接梁法，美国AASHTO LRFD方法等[1- 4]。实际桥梁往往因为环境因素及养护不足等导致结构性能退化[5]。对在役桥梁若仍采用上述方法，忽略横向联系结构损伤，将会导致计算结果与实际荷载横向分布误差增大。本文在考虑各主梁间湿接缝刚度损伤条件下，重新推导刚接梁法计算公式，对在役桥梁荷载横向分布作出正确评价，并结合有限元仿真结果加以验证。

1 修正刚接梁法计算原理

1.1 基本假设

以简支梁桥为例，为简化分析作基本假设：①各主梁之间依靠湿接缝连接成空间整体受力结构。所谓刚接梁，即假设其各梁之间仅传递竖向剪力和横向弯矩，实际结构中桥面板中产生的纵向剪力，法向力均认为是次要力，忽略不计。②桥上外荷载近似为一个作用在主梁轴线上沿桥梁纵向分布的正弦荷载psin(πx/l)，p为外荷载峰值，x为纵坐标，l为梁跨。

1.2 内力分布

随着桥梁服役年限的增长，温度、收缩、徐变等时变效应和重载交通荷载作用必然会给养护滞后的桥梁带来损伤。假设主梁间湿接缝均发生不同程度的损坏，导致梁间剪力和弯矩的传递发生折减，以5片T梁桥为例，将主梁连接从中间切开加上赘余力素形成基本受力体系。梁间剪力g分别为原来的1/m1，1/m2，1/m3,1/m4，弯矩M分别为原来的1/n1,1/n2,1/n3,1/n4。内力情况如图1所示。

图1 基本体系

根据基本体系则可以建立方程并求解，从而得到各号梁单位正弦荷载下横向分布影响线竖标值，以1号梁为例，各值为

(1)

式中：ηij为j处单位正弦荷载下i处横向分布影响竖标值。

2 力法方程的建立与化简

2.1 建立超静定内力正则方程

由n片梁组成的桥梁，有(n-1)个未知剪力和(n-1)个未知弯矩，考虑相应的内力传递折减系数，根据结构力学力法原理和相邻两根主梁在切开面处竖向相对位移和转角为0的变形协调条件，以荷载作用在1号 梁时5梁式T梁桥为例建立超静定内力正则方程：

(2)

式中:δij为赘余力素前的计算系数，即j单位力在i处引起的变位；[g,M]为赘余力素；Δ为外荷载在i处引起的变位。

根据力与变形之间的关系计算系数值并规定其正负。变位与赘余力素正向一致时取正值，反之取负值，见图2。系数矩阵各系数取值如下。

图2 变形示意

式中:b为单梁宽度;w为单位荷载作用在主梁中央产生的挠度；f为单位荷载作用在梁悬臂端时产生的挠度；φ为单位扭矩产生的截面扭转角；φ′为单位弯矩作用在悬臂端时产生的扭转角；τ为单位弯矩作用在悬臂端时产生的挠曲角。

p作用在1号梁时有：Δ1p=-1;其余Δip=0。

2.2 方程的化简

对简支梁挠曲微分方程EIω‴(x)=psin(πx/l)和扭转微分方程GIφ″(x)=-(b/2)psin(πx/l)分别进行积分求解。当x=l/2，扭矩为(b/2)sin(2x/l)时：跨中挠度w=l4/(π4EI)，跨中扭角φ=bl2/(2π2GJ)。

将系数矩阵每项除以ω，令γ=bφ/(2w)，β=f/w，则有[6]

(4)

混凝土剪切模量G取0.425E,则有

(5)

式中,β′=[b/(2d1)]2β。

故系数矩阵化简后为

3 算例分析

某5梁式20 m预应力简支T梁桥，桥梁宽度B=12.5 m，跨径L=30 m，桥梁宽跨比为B/L=0.42，主梁采用C50混凝土。

利用ANSYS有限元分析软件进行实桥仿真建模，主梁采用Solid 65实体单元，混凝土强度C50，预应力钢筋采用Link 10单元。采用降温法施加预应力，湿接缝单独建立实体单元，改变其刚度特性来模拟结构损伤。假设每段湿接缝损伤后EI均变化为原来的75%，即本文方法中的剪力和弯矩折减系数m=n=4/3，各计算方法均考虑中载两列车后轮作用于跨中的布载形式，具体布置见图3。

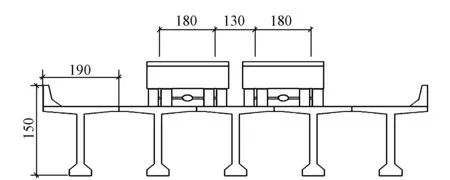
图3 横桥向加载示意(单位：cm)

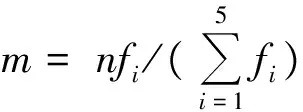
表1 各计算方法在中载下跨中横向分布系数

从表1可见，本文方法考虑湿接缝刚度损伤后导致梁间剪力和弯矩的传递发生折减效应的计算结果和传统刚接梁法计算结果有一定差异。这说明针对在役桥梁的横向分布系数计算时，有必要考虑湿接缝的刚度损伤，本文方法更契合这一特点。在中载工况下，3号梁的横向分布系数增大，1号梁、2号梁均有不同程度的减小。这是因为中载车轮靠近中梁，在湿接缝刚度损伤条件下，中梁挠度会明显增大，但由于剪力和弯矩传递的折减，边梁挠度较未损伤前有所减小。有限元数值方法考虑了湿接缝刚度的损伤，因此与本文方法结果更接近，同样也验证了本文方法的正确性。但仍有些许误差，这是因为传统的刚接梁法和本文方法均未考虑钢筋对梁体刚度的贡献，但有限元分析中输入了预应力钢筋。

4 结论

1)未考虑钢筋对梁体刚度贡献作用的传统刚接梁法计算方法用于桥梁设计，设计承载能力会偏高，是偏安全、保守的。

2)针对在役多梁式桥梁荷载横向分布系数的计算，考虑湿接缝刚度损伤的影响，采用本文方法计算精度较高，更符合实桥状况。

[1]吴向男,徐岳,梁鹏.桥梁结构损伤识别研究现状与展望[J].长安大学学报:自然科学版,2013,33(6):49-58.

[2]陈勇军,张会远.桥梁横向分布系数计算方法对比分析研究[J].公路工程,2015,40(3):148-151.

[3]刘华,叶见曙,俞博,等.桥梁荷载横向分布系数计算方法[J].交通运输工程学报,2009，9(1):62-66.

[4]钱寅泉,周正茂,王素娟.装配式小箱梁桥荷载横向分布数值分析与试验[J].公路交通科技,2012,29(1):86-90.

[5]叶见曙,张峰.预应力混凝土连续箱梁开裂后的刚度退化模型[J].中国公路学报,2007,20(6):67-72.

[6]李国豪，石洞.公路桥梁荷载横向分布计算[M].北京：人民交通出版社,1990.

[7]韦立林,王文宁,王建军.简支梁桥荷载试验横向分布系数分析方法[J].广西大学学报(自然科学版),2007,32(2):183-185.

[8]钟小军.装配式小箱梁桥荷载横向分布系数探究[J].中国市政工程,2013(2):17-19.