重载铁路桥上货物列车脱轨预防措施

龚凯，向俊，毛建红, 2，余翠英



重载铁路桥上货物列车脱轨预防措施

龚凯1，向俊1，毛建红1, 2，余翠英1

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 华东交通大学 土木建筑学院，江西 南昌，330013)

针对重载铁路常见桥梁结构特点，建立货物列车−轨道−桥梁系统(简称“FTTB系统”)空间振动计算模型；按照列车脱轨能量随机分析理论，提出重载铁路FTTB系统横向振动稳定性分析方法。通过算例，计算圆形墩加固前、后FTTB系统横向振动稳定性及其振动响应。研究结果表明：算例中圆形墩加固后FTTB系统抗脱轨能力可提高50%；圆形墩加固前、后FTTB系统横向振动失稳临界车速分别为134.45 km/h和156.99 km/h，容许极限车速分别为107.56 km/h和125.59 km/h；圆形墩加固后货物列车以80 km/h车速过桥时平稳性有保证；与加固前相比，桥梁跨中和墩顶横向位移分别减小54.5%和83.8%。该分析方法能够同时反映货物列车脱轨信息和FTTB系统空间振动特性，可为桥上货物列车脱轨预防措施提供更加全面、科学的评价。

铁道工程；重载铁路；货物列车；横向振动

为克服铁路运输中运能与运量不相适应的问题，国内外大力发展重载铁路[1]。桥梁结构是重载铁路的重要组成部分，并以预应力混凝土T梁桥为主，这在我国大秦线(大同—秦皇岛)及朔黄线(神池南—黄骅港口)上属于常见梁型[1−2]。近年来，随着货物列车轴重日益增大，编组车辆数不断增多，车速不断提高，桥上货物列车脱轨事故时有发生[3]，采取有效措施预防桥上货物列车脱轨十分必要。曾庆元等[3]列车脱轨机理出发，对桥上多次列车脱轨实例进行分析，得出桥梁结构横向刚度不足是诱发桥上列车脱轨的主要原因，并且认为具有足够横向刚度的桥梁结构能够确保桥上列车安全、平稳运行。预防桥上列车脱轨必须增大桥梁结构横向刚度。增大桥梁结构横向刚度的措施很多，其中对于我国大面积的既有桥梁，常采用加固措施增大桥梁结构横向刚度。针对桥梁结构加固措施，国内外学者进行了许多研究。但关于桥梁结构加固后货物列车的抗脱轨安全度尚不清楚。为此，本文作者基于文献[4−5]，建立重载铁路货物列车−轨道−桥梁系统(简称“FTTB系统”)空间振动计算模型，研究现有桥上列车脱轨预防措施评价方法并探讨其不足；按照列车脱轨能量随机分析理论[3]，提出FTTB系统横向振动稳定性分析方法，采用此方法，以重载铁路大秦线某桥圆形墩加固为例，计算桥墩加固前、后FTTB系统横向振动极限抗力做功及其增量，以及列车不脱轨条件下FTTB系统空间振动响应，分析桥墩加固前、后对货物列车运行安全性以及FTTB系统空间振动响应的影响，以便为我国重载铁路货物列车脱轨预防措施的评价方法提供参考。

1 货物列车−轨道−桥梁系统空间振动计算模型

1.1 轨道−桥梁系统空间振动计算模型

沿桥跨方向将轨道、梁跨均划分为个等长单元(简称“梁段单元”)，并取相邻2横隔板间长度作为1个梁段单元，进行如下假定：

1) 将混凝土轨枕与双T梁上翼缘板间的道砟层模拟为线性弹簧及黏滞阻尼器，其竖向、横向弹性系数分别为1和2，竖向、横向阻尼系数分别为1和2，并将道砟层质量分摊给双T梁上翼缘板。

2) 将钢轨与混凝土轨枕间的扣件模拟为线性弹簧及黏滞阻尼器，其竖向、横向弹性系数分别为3和4，竖向、横向阻尼系数分别为3和4。

3) 钢轨视为弹性点支承Euler梁，混凝土轨枕视为不考虑轴向变形的短梁。

4) 对于沿桥跨变截面的双T梁桥，为简化计算，采用等截面单元，取每个梁段单元中点在梁中的实际截面作为该单元的截面特性。

5) 将2片T梁均考虑为上、下翼缘不等边的工字梁，每个单元结点具有3个自由度，分别为主梁横向位移b、竖向位移b及绕其扭转中心的转角b；每片T梁周边不变形，绕其自身扭转中心S转动及形心轴Y横向弯曲时，2片T梁的转角及横向弯曲位移均 相同。

6) 每个桥墩均采用梁单元模拟，桥墩墩顶与主梁梁端连接，并近似认为梁端横向位移与墩顶横向位移相等；桥墩墩底假设与地面固结，不考虑桩基的影响。

梁段单元空间振动分析模型见图1。

为便于建立模型，将双T梁单元节点3个自由度经坐标转换后[3]，采用双T梁4个角点自由度表示。这样，基于上述假定及列车−轨道系统空间振动计算模型[4]和双T梁梁段单元模型[5]，每个梁段单元均可离散为50个自由度的有限元模型，单元节点位移如下：

图1 梁段单元空间振动分析模型

式中：下标1和2分别表示梁段单元的左端和右端节点；上标T，S和B分别表示钢轨、轨枕、桥梁主梁的位移；下标R和L分别表示梁段单元的右侧和左侧；，，和分别为沿桥跨方向纵向线位移、横向线位移、竖向线位移和转角位移；为钢轨沿线路纵向扭转角的变化率；下标U和D分别表示桥梁主梁的上翼缘和下翼缘，下标，和分别为梁跨方向(纵向)、垂直于梁跨的水平方向(横向)、垂直于梁跨的竖直方向(竖向)。

根据式(1)所示的单元节点位移，可导出每个梁段单元的空间振动势能Bj，然后将各梁段单元空间振动势能叠加可得B，再将其与桥墩空间振动总势能P叠加可得轨道−桥梁系统空间振动总势能BP，推导过程见文献[4−5]。

1.2 货物列车空间振动计算模型

将货物列车的机车、车辆均离散为具有26个自由度的多刚体系统，车体和前、后转向架分别考虑3个平动和3个转动自由度，分别为伸缩、横摆、沉浮、点头、侧滚、摇头；每个轮对均考虑横摆和浮沉2个自由度，这样，机车或车辆均有26个自由度。由上述位移模式，即可导出第辆车的空间振动势能Vi，叠加多辆车的空间振动势能可得到列车振动总势能V，推导过程见文献[4]。

1.3 FTTB系统空间振动方程的建立和求解

设在时刻，有辆车运行在重载铁路桥上，此时货物列车空间振动总势能如下：

考虑轮轨“游间”影响的轮轨位移衔接条件，经叠加得到FTTB系统空间振动总势能为

按照弹性系统动力学总势能不变值原理[6]及形成系统矩阵的“对号入座”法则[3]，得出FTTB系统在时刻时的矩阵方程分别为

2 现有桥上列车脱轨预防措施评价方法及其不足

目前，国内外学者针对桥梁加固措施已展开了一些研究，并对桥梁结构加固效果进行了评价。评价方法主要可分为3类，分别为桥梁结构自振特性评价法、动力学指标评价法、列车安全性指标评价法。

1) 桥梁结构自振特性评价法是指通过分析桥梁加固前、后横向自振频率的变化对加固措施进行评 价[7−8]。

2) 动力学指标评价法是通过计算或实测得到桥梁加固前、后桥梁跨中横向、竖向位移或墩顶横向位移等动力响应的变化，进而评价桥梁加固效果[7−13]。

3) 列车安全性指标评价法是指采用脱轨系数、轮重减载率等指标对桥梁加固效果进行评价[7−8]。

上述方法在评价桥梁加固措施效果中取得了许多成果，然而，它们在反映货物列车脱轨信息方面仍存在以下不足：

1) 桥梁结构自振特性评价法仅反映了加固措施对桥梁本身的影响，并没有反映FTTB系统的变化，难以反映桥梁加固后货物列车的脱轨信息。

2) 动力学指标评价法尽管直观地反映了桥梁加固前、后桥梁横向振动响应的变化，但这样的振动响应是在列车正常运行即列车未脱轨条件下获得的，难以反映桥梁加固后对列车抗脱轨能力的影响，并且迄今为止关于桥上列车脱轨时的实测响应尚未见报道。

3) 脱轨系数和轮重减载率作为传统的列车安全性评价指标已进行多次修正，但脱轨系数的根本思想仍未改变。首先，它表达的是轮轨一点接触和开始悬浮的状态，难以表达车轮爬上钢轨的过程；其次，它的限值来源于单个轮对在假定荷载下的理论分析和试验结果，与实际列车运动趋势存在很大差距，难以反映实际的脱轨信息，显然最大值无法确定；最后，脱轨系数和轮重减载率限值对车脱轨缺乏控制作用[3]，很难保证列车在运行过程中它们不发生超限，并且因脱轨概率很小，列车脱轨试验难以实现，列车脱轨瞬间的脱轨系数和轮重减载率的临界值尚未测到。

鉴于上述不足，本文从列车脱轨机理、FTTB系统抵抗列车脱轨的极限能力、FTTB系统横向振动稳定性出发，提出重载铁路FTTB系统横向振动稳定性分析方法，并将此法应用于重载铁路桥上货物列车脱轨预防措施的评价。

3 重载铁路FTTB系统横向振动稳定性分析方法

向俊等[14−15]针对高速列车运行安全性问题提出了列车−轨道(桥梁)系统横向振动稳定性分析方法，分别得到了路基及桥上高速列车的临界车速、容许极限车速等指标。但重载铁路桥梁不同于高速铁路桥梁，货物列车也不同于高速列车，它们组成的列车−轨道−桥梁系统也不相同。可是，上述方法为分析重载铁路桥上货物列车运行安全性奠定了基础。为此，本文提出重载铁路FTTB系统横向振动稳定性分析方法。

3.1 FTTB系统横向振动自激性

货物列车运行在轨道上产生轮轨相互作用，经扣件传至轨枕，轨枕传至道床，再由道床传至桥梁，引起桥梁振动，反过来桥梁振动又引起货物列车、轨道振动，最终形成FTTB系统空间振动。引起FTTB系统竖向振动主要是轨道竖向不平顺及其自重，而引起FTTB系统横向振动的影响因素很多，除轨道横向不平顺外，还包括轮轨缺陷、车轮踏面锥度、车辆载重偏心等，这些因素属于非振动因素，它们伴随着列车运行而产生一些不会衰减的复杂的周期性振动；当货物列车在轨道上停下时，FTTB系统停止振动。可见，FTTB系统具有自激性，该特性使得FTTB系统在货物列车运行过程中不断有能量输入，这些能量来源于上述非振动因素作为FTTB系统内部激励所作的功。

3.2 FTTB系统横向振动最大输入能量σpmax及其增量Δσpr, max的确定

研究表明[5]：机车车辆构架蛇形波是FTTB系统横向振动激振源，并采用构架蛇形波标准差p作为FTTB系统横向振动的输入能量。为获得构架蛇形波标准差p，在多条铁路干线上大量实测构架蛇形波，经统计、计算得到货物列车在各车速下具有99%概率水平的标准差p，并绘制p−曲线。根据该曲线，采用Monte-Carlo法随机模拟出1条具有99%概率水平的构架人工蛇形波作为FTTB系统横向振动的输入能量。

实践表明，列车发生脱轨的概率很小，要进行多次试验才能出现脱轨，但脱轨带来的生命财产损失很大。列车脱轨时FTTB系统横向振动输入能量pmax难以通过实测、统计得到。经实测、统计得到货物列车各车速下具有99%概率水平的构架蛇形波标准差pmax，这里包括列车脱轨和未脱轨时的最大输入能量。根据功能转换原理，系统输入能量越大，引起的振动则越剧烈；反之，振动则越小。列车脱轨机理是FTTB系统横向振动失稳[3]，是FTTB系统小幅横向振动逐渐增大直至失稳的过程。由此说明列车脱轨时的pmax比不脱轨时的p要大很多，而相应的pmax−曲线必在未脱轨的p−曲线之上。pmax−曲线虽不能建立，但可证明其平行于p−曲线[3]。

根据p−曲线可知，列车未脱轨条件下车速0至车速r的FTTB系统横向振动输入能量增量Δpr为

式中：p0和pr分别为车速0和r对应FTTB系统横向振动输入能量；Δ=r−0。同理，根据pmax−曲线可知列车脱轨条件下车速0至车速r的FTTB系统横向振动最大输入能量增量Δpr,max为

式中：p0,max和pr,max分别为车速0和r对应FTTB系统横向振动最大输入能量。

由pmax−曲线平行于p-曲线可知2条曲线斜率相等，即

将式(7)~(8)代入式(9)得

由式(10)表明：列车脱轨条件下FTTB系统横向振动最大输入能量增量Δpr,max可根据列车未脱轨条件下的p−曲线确定。

3.3 FTTB系统横向振动极限抗力作功σc及其增量Δσcr的确定

前已阐明货物列车脱轨时的构架蛇形波难以测得，相应的标准差pmax也无法获得，只能根据列车未脱轨条件下的p−曲线确定列车脱轨条件下FTTB系统横向振动最大输入能量增量Δpr,max，但仅根据Δpr,max还不能确定FTTB系统的稳定性。因为根据现有运动系统稳定性分析理论，当抗力(抗力作功)增量大于荷载(输入能量)增量时，系统稳定；当抗力或抗力做功增量小于荷载或输入能量增量时，系统不稳定；当抗力或抗力作功增量等于荷载或输入能量增量时，系统处于临界失稳状态。判断系统是否稳定须得到系统的抗力或抗力作功增量，而FTTB系统是时变系统，上述方法不能直接被应用，但据能量增量提出如下FTTB系统横向振动稳定性评判准则：

1) 当Δcr＞Δpr时，FTTB系统横向振动是稳定的。

2) 当Δcr＜Δpr时，FTTB系统横向振动不稳定。

3) 当Δcr=Δpr时，FTTB系统横向振动处于失稳临界状态。

上述准则中的Δcr为车速0和r对应的FTTB系统横向振动极限抗力作功之差。FTTB系统横向振动极限抗力作功采用c表示，它具有以下2点意义：

1) 它表示列车脱轨时输入FTTB系统横向振动的能量最大，比它大的输入能量不存在，因为当输入能量达到c时，FTTB系统横向振动已经失稳，列车 脱轨。

2) 它是货物列车脱轨时FTTB系统横向振动所发挥的最大抗力作功，反映了FTTB系统抵抗脱轨能力。其实，c相当于静力压杆稳定性分析中临界荷载cr，该荷载是通过不断增大直至压杆失稳时的荷载。

由此，FTTB系统横向振动极限抗力作功c只能借助仿真计算，采用试算法得到。试算过程如下：假定比正常行车更大的构架蛇形波标准差为p1，按照Monte-Carlo法随机模拟出1条构架蛇形波作为FTTB系统横向振动激振源，并采用轨道竖向几何不平顺作为FTTB系统竖向振动激振源，计算FTTB系统振动响应，检查车轮悬浮量及轮轨横向相对位移是否达到车轮脱轨几何准则要求(该准则认为当车轮悬浮量为25 mm且轮轨横向相对位移为54 mm时，车轮轮缘顶端爬上钢轨顶部中点，车轮即将脱轨掉道)。若达到，则判定车轮脱轨；若未达到，则假定比p1更大的构架蛇形波标准差p2。重复上述步骤，直至车轮悬浮量及轮轨横向相对位移是否达到车轮脱轨几何准则要求为止。

此时，试算完成，采用的构架蛇形波标准差p2为货物列车脱轨时的构架蛇形波标准差，即FTTB系统横向振动极限抗力作功c，相应的振动响应反映了货物列车脱轨全过程。这一试算过程未考虑FTTB系统各结构参数(如机车、车辆、轨道结构、桥梁结构等)的随机性，只考虑了构架蛇形波的随机性，故在FTTB系统各结构参数确定条件下，给定车速，即可算出相应的c，进而建立c−曲线。根据c−曲线，运用差分法可得出FTTB系统横向振动极限抗力作功增量Δcr为

式中：c0和cr分别为车速0和r对应FTTB系统横向振动极限抗力作功。

3.4 FTTB系统横向振动稳定性评价指标

根据计算得到的FTTB系统横向振动极限抗力做功增量Δcr及其最大输入能量增量Δpr，将Δcr=Δpr时对应的车速称为FTTB系统横向振动失稳临界车速(简称临界车速，记作cr)。由cr除以安全系数，可得控制货物列车安全运行的容许极限车速L，将取为1.25作为安全系数。由此，建立一套货物列车安全运行控制指标为临界车速cr、容许极限车速L。然后，将小于L的列车实际运行速度判定为安全，并采用国际通用的Sperling平稳性指标检算货物列车运行平稳性是否达到要求。

采用上述指标评价预防货物列车脱轨的桥梁加固措施。具体评价过程为：计算桥梁加固前、后FTTB系统横向振动极限抗力作功c随车速的变化，分别绘制c−曲线，并计算桥梁加固前、后FTTB系统横向振动极限抗力作功的增量Δc及其输入能量增量Δp, 按照上述FTTB系统横向振动稳定性评判准则，判断FTTB系统横向振动是否失稳，找到Δc=Δp时车速，该车速即为临界车速。按照安全系数1.25分别计算桥梁加固前、后FTTB系统的容许极限车速L，以此分析桥梁加固前、后FTTB系统的容许极限车速L的变化。同时，以L为基础，计算桥梁加固前后货物列车以小于L的车速运行时FTTB系统的空间振动响应，分析桥梁加固对FTTB系统的空间振动响应的变化。采用国际通用的Sperling指标检算桥梁加固前、后货物的平稳性是否满足要求：若满足，则该措施即为能够预防货物列车脱轨的加固措施；若不满足，则选择横向刚度更大的桥梁加固措施。按照上述步骤进行评价，直至达到预防货物列车脱轨的要求 为止。

4 实例分析

鉴于重载铁路桥梁中、高墩因横向刚度不足易对行车安全产生不利影响[16]，以大秦线某桥圆形墩加固[9]为例进行分析。圆形墩全高为17.6 m，墩高为 13.0 m，上部墩身高为8.0 m，下部墩身高为5.0 m，上部直径为2.0 m，下部直径为2.4 m。选取文献[9]中单线桥梁加固方案14作为研究对象。该方案为圆形墩加固高度为0.6倍墩身高，在加固高度范围内的墩身横截面加固为圆端形，墩身横向为墩身直径增大2.0 m，墩身纵向为墩身直径增大0.5 m。梁跨结构为大秦线常见跨度32.0 m预应力混凝土双T梁桥，桥型为参标桥2019。为反映多跨桥梁加固前、后对货物列车运行安全性的影响，选取7跨32.0 m预应力混凝土简支梁单线桥作为计算对象，直线桥，有砟轨道为60 kg/m钢轨、II型混凝土轨枕、碎石道砟。由实测和理论计算结果可知全列空载货车发生脱轨概率最大[17]，并鉴于重载铁路敞车占比较大，不失一般性，列车计算编组为1辆机车牵引15辆空载敞车。

当列车速度为90 km/h及以上时，FTTB系统横向振动输入能量的货物列车构架蛇形波标准差p由文献[3]中方法得到；当列车速度为90 km/h以上时，p按照文献[5]中方法得到，形成p−曲线，如图2所示。在判别本文算例圆形墩加固前、后FTTB系统横向振动稳定性时，桥梁加固前、后FTTB系统横向振动输入能量p均按照图2中的p−曲线选取。实际上，圆形墩加固会提高桥梁结构横向刚度，使得FTTB系统横向振动输入能量小于圆形墩加固前FTTB系统横向振动输入能量，但鉴于目前尚缺乏桥梁加固后FTTB系统横向振动输入能量等相关数据，本文在计算中采用圆形墩加固前FTTB系统横向振动输入能量作为桥梁加固后FTTB系统横向振动输入能量。可以想象：若加固后的桥梁结构能抵抗该输入能量，则实际加固效果将优于计算结果，由此可为实际桥梁加固后货物列车提供更大的安全裕量。

图2 FTTB系统横向振动输入能量σp随车速v的变化

4.1 圆形墩加固前、后对货物列车走行安全性分析

鉴于我国货物列车脱轨速度大多在50 km/h以上，故以50 km/h作为检算起点[3]。同时，考虑到计算和测试误差，车速每增加10 km/h检算1次FTTB系统横向振动稳定性。按照重载铁路FTTB系统横向振动稳定性分析方法，计算上述算例圆形墩加固前、后货物列车脱轨全过程，得到圆形墩加固前、后FTTB系统横向振动极限抗力作功c，相应的c−曲线如图3所示。圆形墩加固前、后FTTB系统横向振动稳定性计算结果分别见表1和表2。

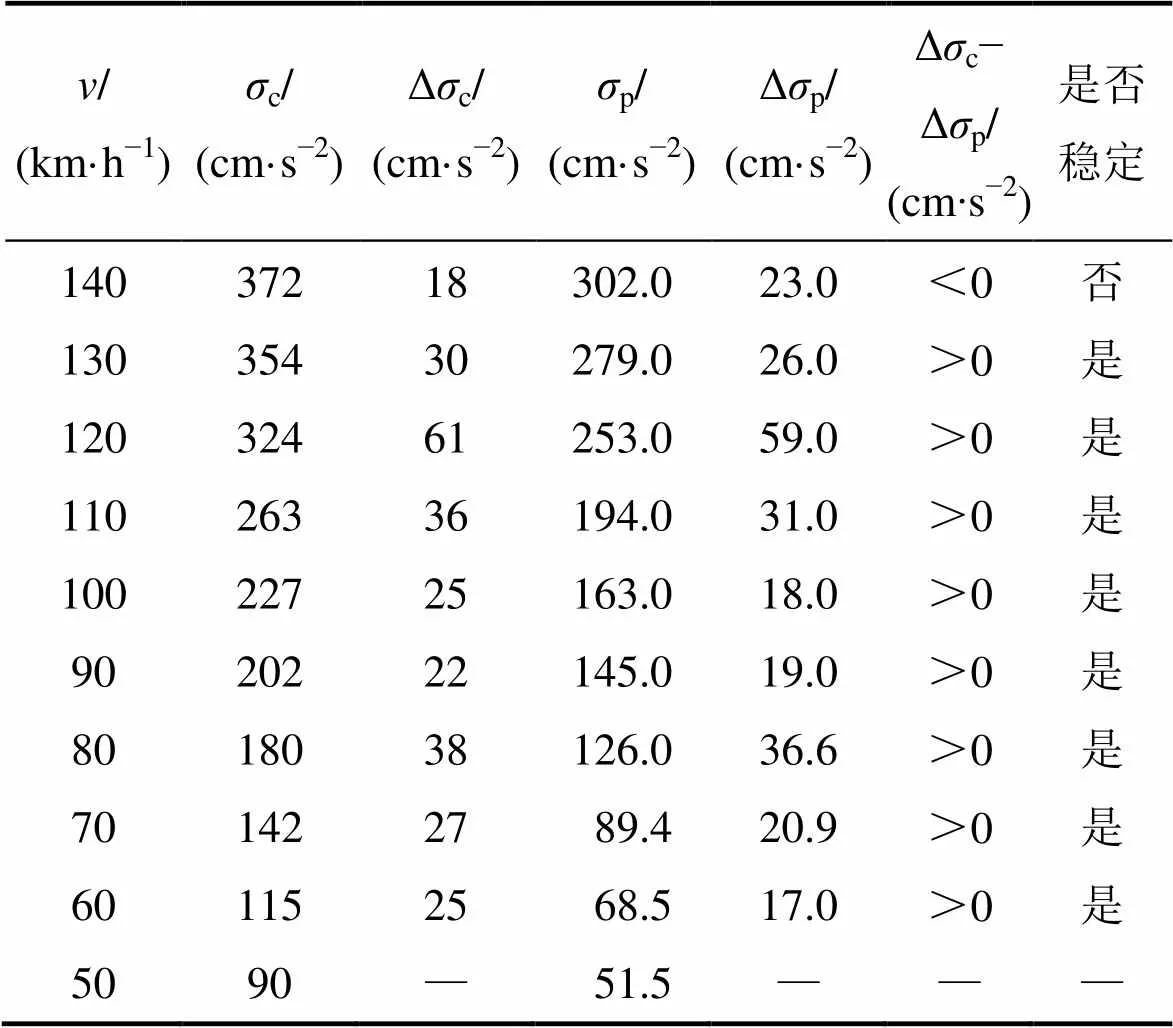
表1 圆形墩加固前FTTB系统横向振动稳定性计算结果

表2 圆行墩加固后FTTB系统横向振动稳定性计算结果

由图3可见：圆形墩加固前、后FTTB系统横向振动极限抗力作功c均随车速增大而逐渐增大；加固前FTTB系统横向振动极限抗力作功c最大为372 cm/s2，加固前后FTTB系统横向振动极限抗力作功c最大为558 cm/s2，圆形墩加固后FTTB系统抗脱轨能力较加固前提高50%。

1—加固前；2—加固后。

同时，由表1可知：圆形墩加固前，随着车速提高，在车速为130~140 km/h时FTTB系统横向振动极限抗力作功c的变化趋势与该系统输入能量p的变化趋势相同。按照内插法，当Δcr=Δpr时，FTTB系统横向振动失稳临界车速cr为134.45 km/h。考虑安全系数为1.25，圆形墩加固前FTTB系统容许极限L为107.56 km/h。

同理，根据表2可知：圆形墩加固后，在车速为150~160 km/h时FTTB系统横向振动极限抗力作功c的变化趋势与该系统输入能量p的变化趋势相同。按照内插法，当Δcr=Δpr时，FTTB系统横向振动失稳临界车速cr为156.99 km/h。考虑到安全系数为1.25，故圆形墩加固后FTTB系统容许极限L为125.59 km/h。

可见：当安全系数为1.25时，圆形墩加固后FTTB系统容许极限车速较桥梁加固前提高16.8%，圆形墩加固后有助于提高FTTB系统容许极限车速，由此说明桥梁加固可提高货物列车运行的安全储备。

4.2 圆形墩加固对FTTB系统空间振动响应的影响分析

根据前面得到的圆形墩加固前、后FTTB系统容许极限L，计算桥梁加固前、后货物列车不脱轨(即＜L)条件下FTTB系统空间振动响应。货物列车车速=80 km/h，计算货物列车正常运行条件下圆形墩加固前、后FTTB系统空间振动响应。这里主要针对圆形墩加固前、后车体横向、竖向Sperling平稳性指标，桥梁跨中上翼缘横向位移、桥梁跨中左腹板竖向位移、墩顶横向位移等时程响应进行分析，结果分别如图4~8所示。

图4和图5所示分别为圆形墩加固前、后桥梁跨中上翼缘横向位移和墩顶横向位移时程曲线。由图4可见：圆形墩加固前、后桥梁跨中上翼缘横向位移最大值分别为4.53 mm和2.06 mm，圆形墩加固后桥梁跨中上翼缘横向位移减小54.5%。由图5可见：圆形墩加固前、后墩顶横向位移最大值分别为2.97 mm和0.48 mm，圆形墩加固后墩顶横向位移减小83.8%。可见：圆形墩加固后桥梁跨中上翼缘横向位移及墩顶横向位移减小明显，有助于增强桥梁结构横向稳定性。

图6所示为第5车车体横向Sperling平稳性指标时程曲线。由图6可见：圆形墩加固前、后第5车车体横向Sperling平稳性指标最大值为4.73和4.21，圆形墩加固后第5车车体横向Sperling平稳性指标减小10.9%。根据我国铁道车辆动力学性能评定和试验鉴定规范[22]可知，圆形墩加固前第5车车体横向Sperling平稳性指标最大值超过合格标准值(4.25)[18]，圆形墩加固后第5车车体横向Sperling平稳性指标最大值小于4.25。可见，在本文算例中，圆形墩加固后，货物列车以80 km/h过桥时的运行平稳性有保证。

1—加固后；2—加固前。

1—加固后；2—加固前。

图7和图8所示分别为圆形墩加固前、后桥梁跨中左腹板竖向位移和第5车车体竖向Sperling平稳性指标时程曲线。由图7和图8可见：圆形墩加固对桥梁跨中左腹板竖向位移和第5车车体竖向Sperling平稳性指标影响较小。

1—加固后；2—加固前。

1—加固后；2—加固前。

1—加固后；2—加固前。

5 结论

1) 基于列车−轨道(桥梁)系统空间振动分析方法及列车脱轨能量随机分析理论，建立了货物列车−轨道−桥梁系统空间振动计算模型；提出了重载铁路FTTB系统横向振动稳定性分析方法；以大秦线某桥圆形墩加固为例，实现了圆形墩加固前、后FTTB系统横向振动稳定性及货物列车正常过桥时FTTB系统空间振动分析。

2) 在本文算例中，圆形墩加固后FTTB系统抗脱轨能力较加固前提高50%；圆形墩加固前、后FTTB系统横向振动失稳临界车速分别为134.45 km/h和156.99 km/h，容许极限车速分别为107.56 km/h和125.59 km/h，圆形墩加固后的容许极限车速较加固前提高16.8%。

3) 在本文算例中，圆形墩加固后，货物列车以车速80 km/h正常过桥(即不发生脱轨)，桥梁跨中上翼缘横向位移减小54.5%，墩顶横向位移减小83.8%。可见：圆形墩加固对削减墩顶横向位移作用明显，并且桥梁跨中横向位移也随之减小，桥梁结构横向稳定性得到了增强；同时，车体横向Sperling平稳性指标最大值未超过规范要求的合格标准，且相比圆形墩加固前车体横向Sperling平稳性指标减小10.9%，货物列车运行平稳性有保证。

4) 本文提出的重载铁路FTTB系统横向振动稳定性分析方法对预防货物列车脱轨的桥梁加固措施进行了全面、科学的评价，不仅可为预防列车脱轨的重载铁路桥梁加固措施提供一种新的评价方法，而且可为重载铁路桥梁设计提供参考。

[1] 耿志修. 大秦铁路重载运输技术[M]. 北京: 中国铁道出版社, 2009: 187−188. GENG Zhixiu. Heavy-haul transportation technologies on Datong—Qinhuangdao Railway[M]. Beijing: China Railway Press, 2009: 187−188.

[2] 李进洲, 余志武. 大轴重列车对既有线32 m预应力混凝土简支T梁的疲劳影响研究[J]. 铁道标准设计, 2014, 58(10): 56−61.LI Jinzhou, YU Zhiwu. Study on the effect of fatigue in 32 m-span PC simply supported T-type beams on existing line due to heavy-haul transport[J]. Railway Standard Design, 2014, 58(10): 56−61.

[3] 曾庆元, 向俊, 周志辉, 等. 列车脱轨分析理论与应用[M]. 长沙: 中南大学出版社, 2006: 204−276. ZENG Qingyuan, XIANG Jun, ZHOU Zhihui, et al. Analysis theory and application of train derailment[M]. Changsha: Central South University Press, 2006: 204−276.

[4] XIANG Jun, LI Dejian, ZENG Qingyuan. Simulation of spatially coupling dynamic response of train track time variant system[J]. Journal of Central South University of Technology, 2003, 10(3): 226−230.

[5] 曾庆元, 郭向荣. 列车桥梁时变系统振动分析理论与应用[M]. 北京: 中国铁道出版社, 1999: 21−29.ZENG Qingyuan, GUO Xiangrong. Theory and application of train-bridge time-variant system vibration analysis[M]. Beijing: China Railway Press, 1999: 21−29.

[6] ZENG Qingyuan, LOU Ping, XIANG Jun. The principle of total potential energy with stationary value in elastic system dynamics and its application to the analysis of vibration and dynamic stability[J]. Journal of Huangzhong University of Science & Technology (Urban Science Edition), 2002, 19(1): 7−14.

[7] 牛斌, 李新民, 马林. 京山线沙河特大桥预应力混凝土梁提速加固设计研究[J]. 中国铁道科学, 2004, 25(6): 65−70. NIU Bin, LI Xinmin, MA Lin. Speed-increased reinforcement design for the prestressed concrete beam of Shahe extra-long bridge on Beijing—Shanghaiguan railway line[J]. China Railway Science, 2004, 25(6): 65−70.

[8] 韩燕, 夏禾, 张楠. 列车提速下32m PC简支T梁的横向刚度方案研究[J]. 铁道学报, 2005, 27(1): 90−95. HAN Yan, XIA He, ZHANG Nan. Study on lateral rigidity reinforcement schemes for 32 m simply-supported PC T-beams under train speed raising[J]. Journal of the China Railway Society, 2005, 27(1): 90−95.

[9] PUURULA A M, ENOCHSSON O, SAS G, et al. Loading to failure and 3D nonlinear FE modeling of a strengthened RC bridge[J]. Structure andInfrastructure Engineering, 2014, 10(12): 1606−1619.

[10] RICHARD B, EPAILLARD S, CREMONA C. Nonlinear finite element analysis of a 50 years old reinforced concrete trough bridge[J]. Engineering Structure, 2010, 32(12): 3899−3910.

[11] ZHANG Rui, MATSUMOTO K, HIRATA T, et al. Application of PP-ECC in beam-column joint connections of rigid-framed railway bridges to reduce transverse reinforcements[J]. Engineering Structures, 2015, 86: 146−156.

[12] D’AMBRISI A, FOCACCI F, CAPORALE A. Strengthening of masonry-unreinforced concrete railway bridges with PBO-FRCM materials[J]. Composite Structures, 2013, 102: 193−204.

[13] GHAFOORI E, MOTAVALLI M, NUSSBAUMER A, et al. Design criterion for fatigue strengthening of riveted beams in a 120-year-old railway metallic bridge using pre-stressed CFRP plates[J]. Composites: Part B, 2015, 68: 1−13.

[14] 向俊, 龚凯, 毛建红, 等. 高速列车运行安全性与桥梁防撞墙受力分析[J]. 铁道学报, 2011, 33(12): 83−87. XIANG Jun, GONG Kai, MAO Jianhong, et al. Analysis on the running safety of high-speed train and the force of bridge collision-proof wall[J]. Journal of the China Railway Society, 2011, 33(12): 83−87.

[15] 向俊, 曾庆元. 列车−轨道(桥梁)时变系统横向振动稳定性与失稳临界车速分析方法[J]. 交通运输工程学报, 2011, 11(1): 19−24.XIANG Jun, ZENG Qingyuan. Analysis method of stability and critical speed for train-track(bridge) time-variable system under lateral vibration condition[J]. Journal of Traffic and Transportation Engineering, 2011, 11(1): 19−24.

[16] 李运生, 阎贵平, 钟铁毅.影响铁路桥梁行车安全的因素: 桥墩横向刚度问题的研究[J].中国安全学报, 2004, 14(2): 98−101. LI Yunsheng, YAN Guiping, ZHONG Tieyi. Influencing factors of running safety on railway bridge: study on lateral pier stiffness[J]. China Safety Science Journal, 2004, 14(2): 98−101.

[17] 向俊, 孔凡兵, 曾庆元. 货物列车编组对列车−桥梁系统空间振动的影响[J]. 中南大学学报(自然科学版), 2007, 38(2): 345−350. XIANG Jun, KONG Fanbing, ZENG Qingyuan. Influence of freight train formation on spatial vibration of train-bridge system[J]. Journal of Central South University (Science and Technology), 2007, 38(2): 345−350.

[18] GB 5599—1985, 铁道车辆动力学性能评定和试验鉴定规范[S]. GB 5599—1985, Railway vehicle-specification for evaluation the dynamic performance and accreditation test[S].

(编辑 陈灿华)

Derailment precautions of freight train on bridge in heavy haul railway

GONG Kai1, XIANG Jun1, MAO Jianhong1, 2, YU Cuiying1

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China)

Considering the general structure characteristics of bridges in heavy haul railway, the freight train−track−bridge(FTTB) system spatial vibration calculation model was established. Meanwhile, based on the random energy analysis theory of train derailment, the analysis method of lateral vibration stability of FTTB system was proposed. Through a calculation example, the lateral vibration stability and the corresponding vibration response of FTTB system before and after the reinforcement of the circular pier were calculated. The results show that the anti-derailment capacity of FTTB system increases by 50% after the circular pier reinforcement in the calculation example. Before and after the circular pier reinforcement, the lateral vibration critical speed of FTTB system is 134.45 km/h and 156.99 km/h, and the admissible limit speed is 107.56 km/h and 125.59 km/h, respectively. After the reinforcement, the operation stability of freight train is guaranteed when the freight train passes over the bridge with speed of 80 km/h. Moreover, the lateral displacements of the bridge mid-span and the top of the pier are reduced by 54.5% and 83.8%, respectively, compared with those before the reinforcement. In conclusion, this method reflects not only the freight train derailment information but also the spatial vibration characteristic of FTTB system. It can provide more comprehensive and scientific evaluation for the derailment precautions of the freight train.

railway track engineering; heavy haul railway; freight train; lateral vibration

10.11817/j.issn.1672−7207.2017.12.035

U213.2

A

1672−7207(2017)12−3406−09

2016−12−20；

2017−03−10

国家自然科学基金委员会与神华集团有限公司联合资助项目(U1261113)；高等学校博士学科点专项科研基金资助项目(20100162110022)；牵引动力国家重点实验室开放课题资助项目(TPL0901，TPL1214)；江西省青年科学基金资助项目(20142BAB216003) (Project(U1261113) jointly supported by the National Natural Science Foundation Committed of China and Shenhua Group Corporation Limited; Project(20100162110022) supported by the Special Fund for Doctor Programs in Institutions of Higher Learning of China; Projects (TPL0901,TPL1214) supported by the Open Program of the Traction Power State Key Laboratory; Project(20142BAB216003) supported by Science Foundation of Jiangxi Province for Youths)

向俊，教授，博士研究生导师, 从事列车脱轨控制、列车−轨道(桥梁)系统空间振动及铁路轨道结构等研究；E-mail：jxiang@csu.edu.cn