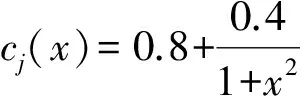具有变时滞的高阶BAM神经网络在有限时间内的控制同步
蒲 浩, 王来全, 刘衍民, 刘向虎
(1.遵义师范学院 数学学院, 贵州 遵义 563006; 2.昌吉职业技术学院 基础部, 新疆 昌吉 831100)
BAM神经网络在1987年被Koskos提出[1], 在不同领域有着重要的应用, 如模式识别、图像处理、 优化问题等. 为此, 研究者对BAM神经网络进行了广泛深入的研究[2-4].
与一阶神经网络相比较而言, 高阶神经网络在网络的收敛速度、 储存水平、 逼近能力等方面有一定的优势. 然而, 研究者主要考虑了一阶BAM神经网络解的稳定性问题及驱动系统和响应系统的同步问题[5-6], 如文献[6]中作者研究了脉冲对具有变时滞模糊BAM细胞神经网络的全局指数同步的影响, 而没有对高阶BAM神经网络的同步问题进行研究.
文献中提到神经网络的指数同步指在无限长时间内实现同步, 而出于效益的考虑, 要求神经网络在较短时间内实现同步.为此神经网络在有限时间内能否实现同步的问题被广泛研究[7-8], 如文献[8]中作者通过自适应反馈控制的方法研究了一类具有混沌和超混沌系统在有限时间内的同步.
本文将对具有变时滞的高阶BAM神经网络在有限时间内的同步问题进行研究.
1 模型和预备知识
考虑如式(1)的具有变时滞的高阶BAM神经网络系统
(1)
式中: 1≤i,j≤n;xi(t),yi(t)表示在t时刻第i层和第j层神经元之间的状态变量;fj(·),gj(·) 表示激活函数;aij,pij,bijl,qijl表示连接权重; 0≤τij(t)≤τ, 0≤σij(t)≤σ表示t刻信号在神经元之间的转换时滞.
对应于系统 (1)的初值条件为

式中:φ(s)=(φ1(s),φ2(s), …,φn(s))T,φ(s)=(φ1(s),φ2(s), …,φn(s))T∈C=([t0-τ,t0],Rn), 指的是把[t0-τ,t0] 映射到Rn上的所有连续函数组成的一个具有p-范数的Banach空间(p≥2是一个正整数), 其中r-范数在本文中定义形式为
(3)
对于系统(1), 我们假设
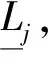
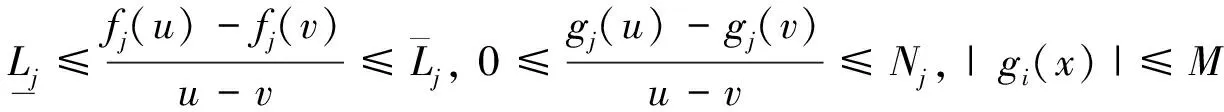
对所有的u,v∈R,u≠v和1≤i,j≤n都成立.
对所有的x,y∈R,x≠y和1≤i,j≤n都成立.
令
把系统 (1) 作为主驱动系统, 则从系统为
(5)
式中:Ti(t),Zj(t)(1≤i,j≤n)表示外部控制输入.
从系统(5)的初值条件是

为了书写方便, 记
由系统(1)和系统(5), 我们可以得到误差系统, 即
(7)
式中:Ti(t)和Zj(t)是控制输入项, 为
Ti(t)=
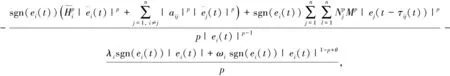
Zj(t)=
定义1 对于主驱动系统(1)和响应系统(5), 设存在一个常数T>0, 使得
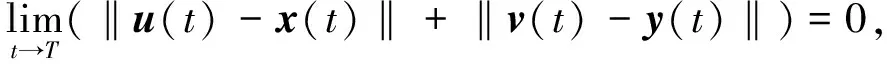
同时, 当t>T时, ‖u(t)-x(t)‖=0和‖v(t)-y(t)‖=0, 则称主驱动系统(1)和响应系统(5)在有限时间(t0,T]内同步.
2 辅助引理
引理1[9]对任意的非负实数a和b,不等式pap-1b≤(p-1)ap+bp,p≥2成立.
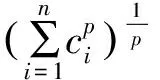
引理3[11]对任意的非负实数a和b, 且0 引理4[12]存在一个连续且正定的函数V(t), 常数λ>0, 0<θ<1, 若微分不等式 成立, 则对任意给定的t0, 不等式 V1-θ(t)≤V1-θ(t0)-λ(1-θ)(t-t0),t0≤t≤T 证明构造 Lyapunov 函数 (8) 结合式(7), H1)和H2)及引理1, 对V(t)关于t计算 Dini 右上导数, 可以得到 (10) 根据引理2可知 (11) 根据引理3和式(11)可知 由式(12)可知 根据引理4可知 注1 在较早的文献中[9], 神经网络的指数要在无限时间内才能实现同步. 出于效益的考虑, 工程领域需要神经网络在较短的时间内实现同步. 本文通过有限时间稳定性理论, 研究了具有变时滞高阶BAM神经网络在有限时间内的同步, 更加实用有效. 范数p=2, 且主驱动系统(1)和响应系统(5)中没有高阶项是本文的特殊情况. 主驱动系统为 (13) 对所有的u,v∈R,u≠v和1≤i,j≤n都成立. 响应系统为 (14) 式中:mi(t),nj(t)为外部输入控制, 即 mi(t)= nj(t)= 记 注2 高阶BAM神经网络在有限时间内实现同步的过程中, 由于系统自身和外界因素对高阶BAM神经网络在有限时间内实现同步有影响, 如脉冲、 反应扩散、 随机扰动、 时滞等, 故对带有脉冲、 反应扩散、 随机扰动和时滞的高阶BAM神经网络在有限时间内的同步问题需要进行进一步研究. 在驱动系统(1)和响应系统(5)中, 取 b111=2.3,b121=-0.25,b211=-1.48,b221=1.2,c112=-2.48,c122=-0.45,c212=0.22,c222=-2.q111=2.1,q121=-0.29,q211=-2.48,q221=1.2,q112=-2.45,q122=-4.6,q212=0.25,c222=-3. 由上述数据计算可得 |b122|=32.03, |b222|=26.01, |q122|=91.11, |q222|=50.02, 经过计算得ω1=4.2,ω2=3,k1=5,k2=6.1, 可知a=3. [1] Kosko B. Bidirectional associative memories[J]. IEEE Trans, Man Cybern, 1988, 18: 49-60. [2] Bao Hongmei. Existence and exponential stability of periodic solution for BAM fuzzy cohen-grossberg neural networks with mixed delays[J]. Neural Processing Letters, 2016, 43(3): 871-885. [3] Sun Gai. Exponential stability of impulsive discrete-time stochastic BAM neural networks with time-varying delay[J]. Neurocomputing, 2014, 131(7): 323-330. [4] Mathiyalagan K, Ju H P. Synchronization for delayed memristive BAM neural networks using impulsive control with random nonlinearities[J]. Applied Mathematics Computation, 2015, 259(C): 967-979. [5] Liu Bingwen. Global exponential stability for BAM neural networks with time-varying delays in the leakage terms[J]. Nonlinear Analysis: Real World Applications, 2013(14): 559-566. [6] Li Kelin. Impulsive effect on global exponential stability of BAM fuzzy cellular neural networks with time-varying delays[J]. International Journal of Systems Science, 2010, 42(2): 131-142. [7] Yang Xinsong. Finite-time synchronization of coupled discontinuous neural networks with mixed delays and nonidentical perturbations[J]. Journal of the Franklin Institute, 2015, 352: 4382-4406. [8] Vincent U E, Guo R. Finite-time synchronization for a class of chaotic and hyperchaotic systems via adaptive feedback controller[J]. Physics Letters A, 2011(375): 2322-2326. [9] Yu Juan, Hu Cheng, Jiang Haijun. Exponential lag synchronization for neural networks with mixed delays via periodically intermittent control[J]. Chaos, 2010, 20(2): 023108-8. [10] Jiang Nan, Liu Xiaoyang. Finite-time stochastic synchronization of genetic regulatory networks[J].Neurocomputing, 2015, 167(C): 314-321. [11] Aghababa M P. Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J]. Applied Mathematical Modelling, 2011, 35: 3080-3091. [12] Wang Hua, Han Zhengzhi. Finite-time Chaos synchronization of unified Chaotic system with uncertain parameters[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(5): 2239-2247.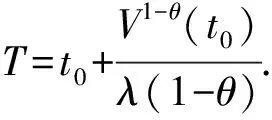
3 主要结果
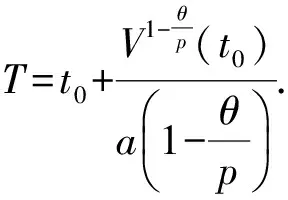
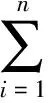
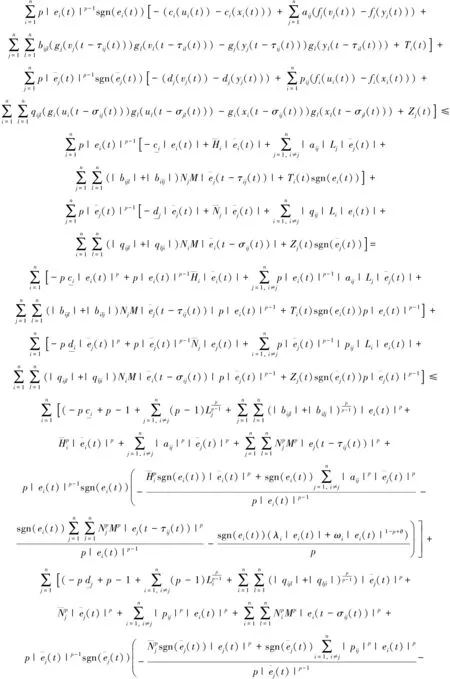
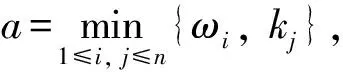
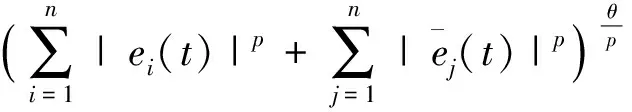
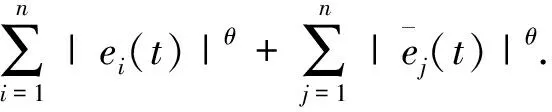

4 推 论
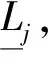
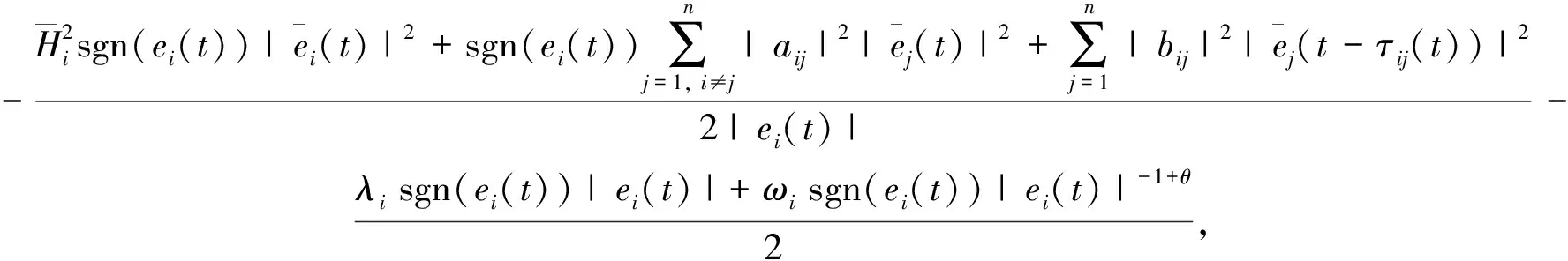

5 数值例子