Z形截面柱抗剪性能有限元分析及工程建议
毛晓飞,章雪峰
(1.浙江保利房地产开发有限公司,浙江 杭州 310014; 2.浙江工业大学工程设计集团有限公司,浙江 杭州 310012)
由于Z形截面柱受力的复杂性致使当前国内外对它的研究相对较少。在抗剪性能方面,同济大学[1]进行的6根宽肢Z形截面柱抗剪性能试验,和浙江工业大学[2]进行的3根Z形截面柱(非宽肢)的抗剪性能试验,都是沿惯性矩较小工程轴方向作用水平力。北京工业大学[3]虽然进行了沿惯性矩较大工程轴方向作用水平力的Z形截面柱抗剪性能试验,但其试件数目只有一个,还不能为我们比较全面地揭示Z形截面柱惯性矩较大工程轴方向的抗剪性能。而在多数情况下Z形截面柱在两水平翼缘方向有连系梁与其相连,框架梁会给柱身传来沿惯性矩较大工程轴方向作用的水平力。且由于惯性矩较大工程轴方向柱肢截面有效高度较另一工程轴要小很多,故其斜截面受剪承载力会比惯性矩较小工程轴方向低,更易发生受剪破坏。因此有必要对Z形截面柱的惯性矩较大工程轴方向的抗剪性能作深入研究。
本文在试验基础上[4],采用通用有限元软件建立数值模型,对25根沿惯性矩较大工程轴方向受力的Z形截面柱进行非线性数值模拟计算,以拓宽试验的分析范围,进一步研究轴压比、配箍率和剪跨比等对Z形截面柱抗剪性能的影响。最后在上述分析的基础上,提出若干工程建议。
1 模型及加载
1.1 模型的建立
根据大量试算的结果,混凝土采用ANSYS单元库自带的8结点六面体单元——SOLID65。为了在较短的分析周期并且使用较少的计算机资源的前提下得到精度相对较高的模拟结果,试算表明:当模拟混凝土的SOLID65单元尺寸为20 mm×20 mm×40 mm时,每个模型的计算周期约为4 h左右,其分析所得应力状态、构件延性及构件极限抗剪承载力与试验值吻合较好,极限承载力误差为1.3%,构件延性误差为5.3%,见表1。如果把SOLID65单元尺寸减小为10 mm×10 mm×40 mm时,模型的计算周期迅速增加到7 h,而分析所得数据的精度与前者相差不大,极限承载力误差为1.9%,构件延性误差为2.3%,见表1。故正式模拟分析时混凝土单元尺寸取为20 mm×20 mm×40 mm。

表1 试算结果比较表
采用LINK8单元来模拟Z形截面柱中纵筋和箍筋的受力性能,纵筋和箍筋的弹性模量、泊松比、屈服强度,见表2。本构关系采用理想弹塑性模型,通过双线性随动强化模型(Bilinear Kinematic Hardening)完成LINK8单元材料应力-应变曲线的定义。
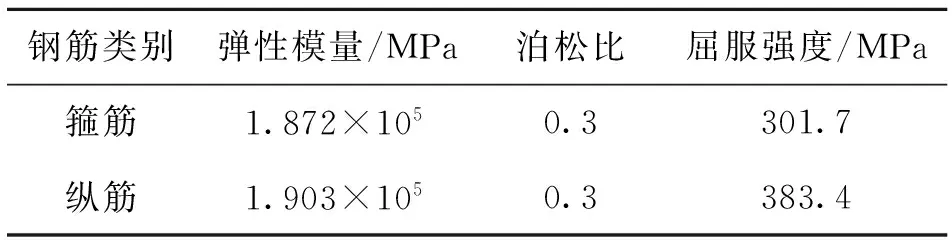
表2 钢筋材料参数表
1.2 加载与求解
本文采用在有限元模型上施加荷载的方法进行加载与约束。根据试验时的约束边界条件可以假定Z形截面柱模型柱底为固端约束,水平支撑顶杆与Z形截面柱的接触面没有水平位移。水平荷载与竖向荷载分别通过两个载荷步施加,第一个载荷步施加竖向荷载,荷载平均作用在Z形截面柱模型柱顶所有节点上。第二个载荷步施加水平荷载, 所有荷载直接作用在相应位置的混凝土单元上。有限元模型加载图见图1。
通过大量的试算,本算例设置了50个子步,同时打开自动时间步长。收敛精度放宽为5%,并且打开线性搜索和时间步长预测-纠正选项,以加速计算的收敛。

图1 有限元模型及加载示意图
2 计算结果与试验结果的对比分析
首先利用已有试验数据的4根试件的试验结果[4]对有限元计算模型进行校验,结果列于表3,由表3可知:模型的ANSYS计算结果与试验结果吻合较好,是可行的。

表3 抗剪承载力比较
注:Vfin为有限元计算结果,Vexp为试验结果。
3 不同因素对Z形截面柱抗剪承载力的影响
在影响柱抗剪承载力的诸多因素中,轴压比、剪跨比和配箍率是主要的结构因素,现分别讨论其影响规律。
3.1 轴压比对试件承载力的影响
根据工程应用条件,确定轴压比的变化范围在0~0.7之间。表4列出了8个有限元模型的极限抗剪承载力计算结果。表中试件只有轴压比取不同数值,其余试验参数均相同,高厚比为3∶1,剪跨比为1.2,配箍为Φ4@160。
图2表示Z形截面柱极限抗剪承载力随着轴压比增加的变化趋势。由图可见:曲线a是一条略微上凸的曲线,当轴压比较小时其斜率相对较大,但随着轴压比的增加斜率不断减小,曲线渐渐趋于水平。该曲线的这一特征所反映抗剪承载力与轴压比的关系是:轴压比较小时,Z形截面柱的抗剪承载力随轴压比的增加而不断增加,但增加速度也不断减缓,当轴压比超过0.5后,构件的抗剪承载力几乎保持一恒定数值。
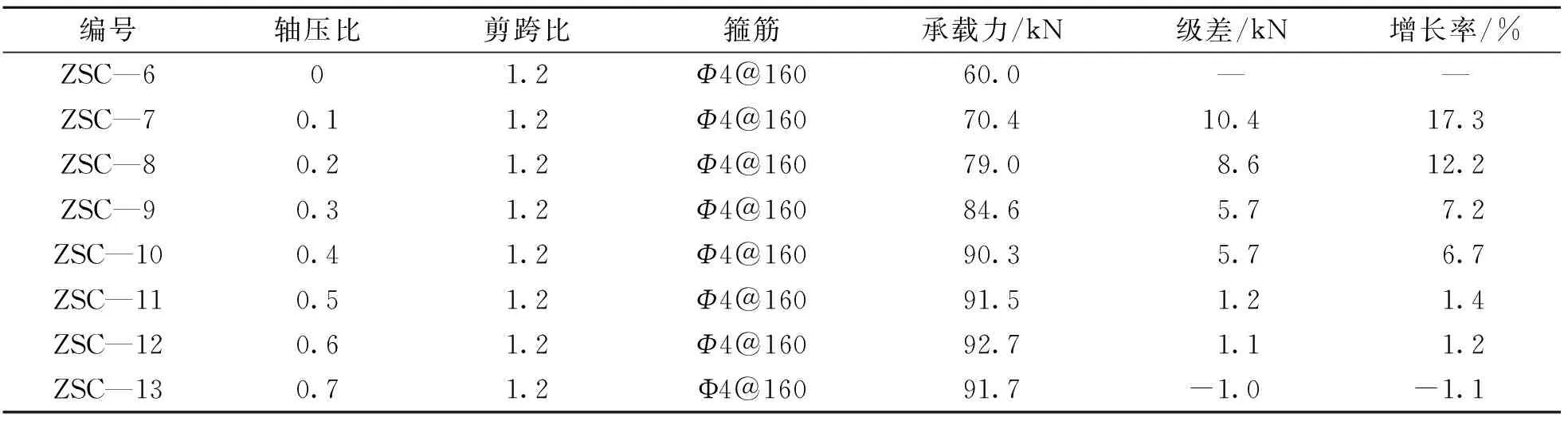
表4 不同轴压比构件的抗剪承载力
注:1)级差:本级承载力与上级承载力之差。2)增长率:本级承载力相对于上级承载力的增长百分数。
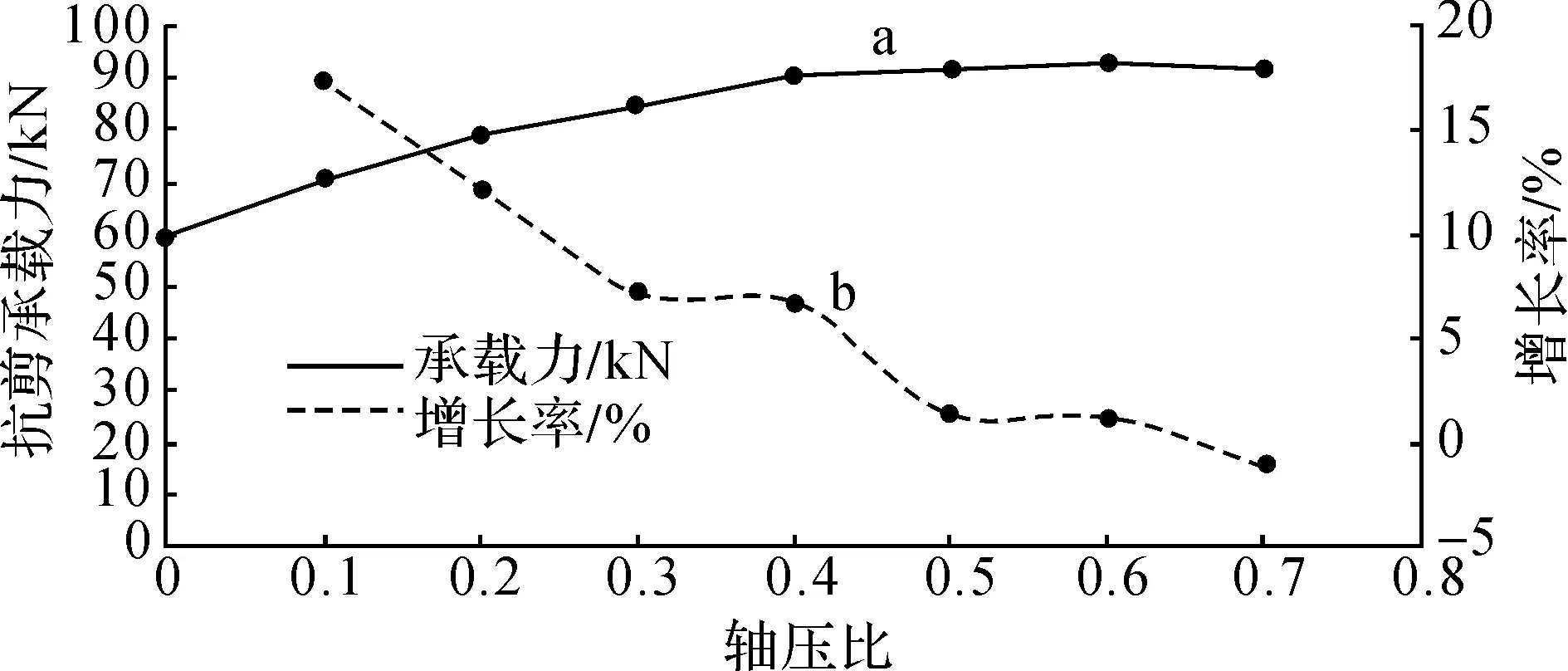
图2 轴压比与抗剪承载力的关系
曲线b表示Z形截面柱抗剪承载力增长率与轴压比的对应关系,总体呈现一直下降的趋势,但随着轴压比的变化可以将曲线b分成以下几个不同的降段:
1)当轴压比在0~0.4范围之内时,增长率最小值是6.7%,平均值是10.9%,故可认为在这一阶段Z形截面柱抗剪承载力随着轴压比的增加有较大提高。而其中在轴压比处于0~0.3范围之内时斜率较陡,说明此阶段轴压比的增加可获得承载力的较快增加,当轴压比在0.3~0.4范围之内时,曲线下降不多,基本保持水平直线,这表明:此阶段抗剪承载力随着轴压比的提高,增长效率下降。
2) 当轴压比在0.4~0.6范围之内时,增长率最小值是1.2%,平均值仅为3.1%,故可认为在这一阶段Z形截面柱抗剪承载力仍然随着轴压比的提高而略有增加或趋于停止增长。
3)当轴压比大于0.6时,Z形截面柱抗剪承载力的增长率曲线又随着轴压比增加而开始有明显下降,当轴压比大于一定数值时,增长率为负值。
因此可以认为轴压比的变化对Z形截面柱抗剪承载力有较大影响,当轴压比在0~0.4范围之内时,轴向压力的增加对抗剪承载能力的提高有较大贡献;当轴压比大于0.6时,继续增加轴向压力,抗剪承载力将出现下降趋势。此分析结果与矩形柱的试验结果也有类似之处,故计算Z形截面柱抗剪承载力时必须考虑轴压比的影响。
3.2 轴压比对试件变形性能的影响
轴压比不仅是Z形截面柱极限抗剪承载力的重要影响因素,也是构件变形性能的重要决定因素。不同轴压比条件下的Z形柱模型的极限位移列于表5。由表5可知:构件极限位移总体是随轴压比的增加而降低,且下降速率随轴压比的不同而变化,其变化规律可由图3反映;在轴压比小于0.5时,极限位移级差随轴压比的增加不断减小;在轴压比大于0.5时,极限位移级差随轴压比的提高迅速增加,这应该可表明当轴压比过大时,在相同的水平力作用下,轴力的约束作用显著增强,使变形迅速下降。
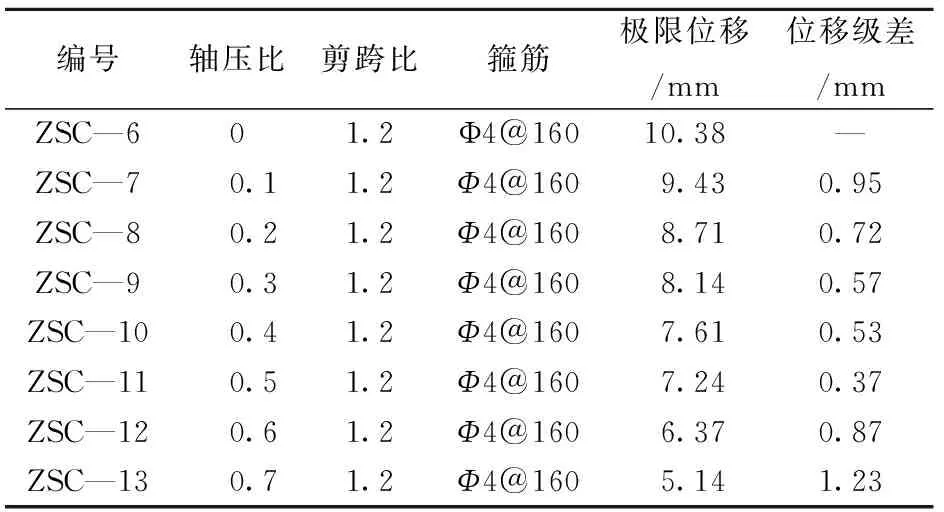
表5 不同轴压比构件的变形性能
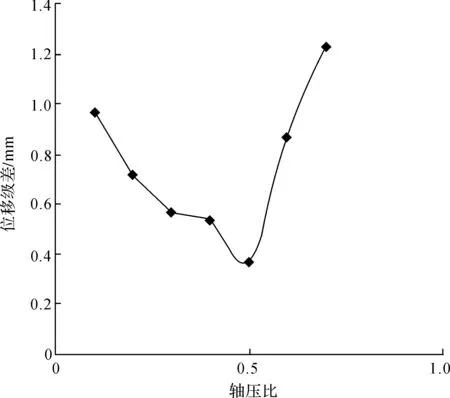
图3 轴压比与位移级差关系图
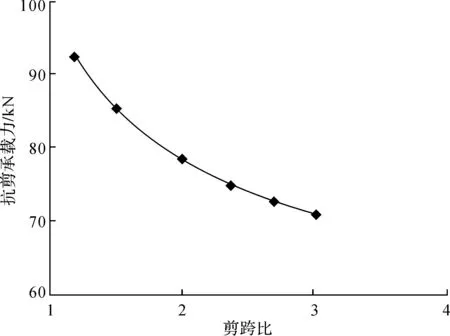
图4 剪跨比与抗剪承载力关系图
3.3 剪跨比对抗剪性能的影响
表6列出了不同剪跨比条件下Z形柱模型的抗剪性能。将表中数据绘成剪跨比与抗剪承载力关系,见图4。从图4可见:Z形截面柱的极限抗剪承载力随着剪跨比的增加而明显降低。且当剪跨比较小时曲线相对较陡,抗剪承载力随着剪跨比的增加下降较快,当剪跨比较大时,这种下降相对趋缓。
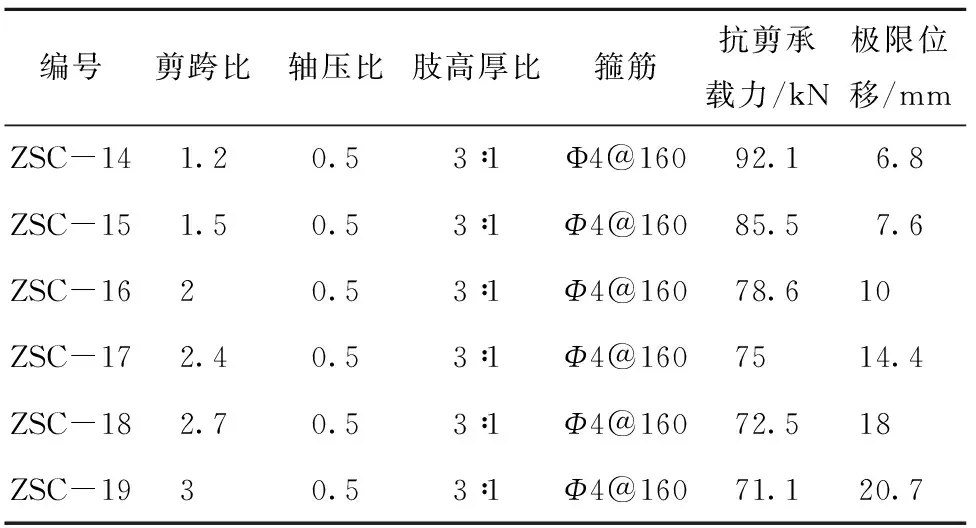
表6 剪跨比对抗剪性能的影响
剪跨比还决定了Z形截面柱的破坏形态,当剪跨比较小时构件破坏形态以剪切破坏为主,随着剪跨比的增加,构件破坏形态中的弯曲破坏成分越来越显著。图5及图6列出了本次模拟所得的两种不同破坏形态的应力云图。其中,λ=1.2、λ=1.5两个构件破坏形态接近,应力云图见图5,λ=2、λ=2.4、λ=2.7、λ=3四个构件破坏形态相近,应力云图见图6。

图5 剪切破坏形态的应力云图
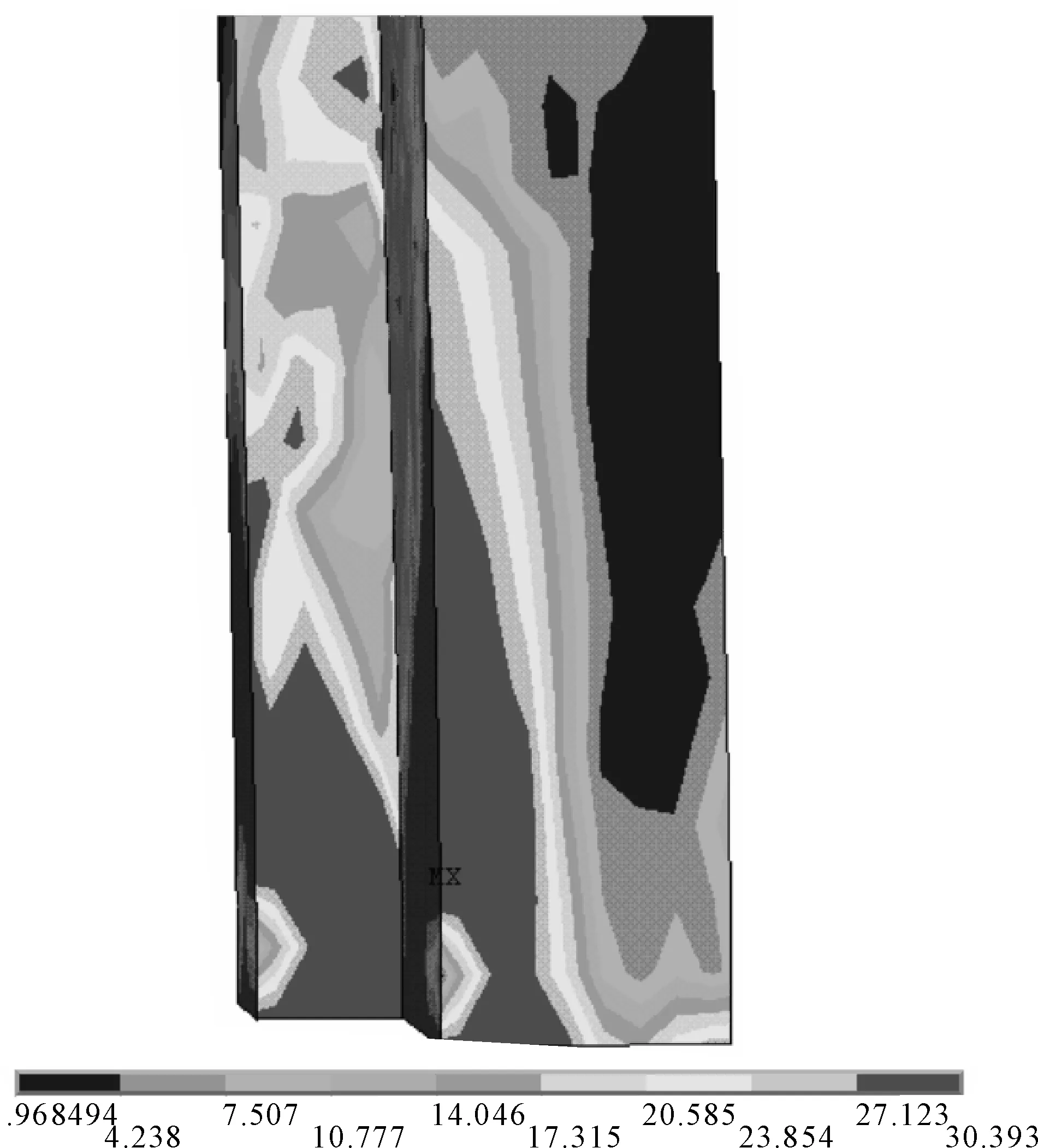
图6 弯曲破坏形态的应力云图
综合可得,极限抗剪承载力随着剪跨比的增加而减小;但其减小幅度随剪跨比的增加而降低。当剪跨比较小(λ≤2)时,Z形截面柱容易产生剪切破坏,随着剪跨比的增加,构件破坏形态中的弯曲成分不断增加,直至弯曲型破坏控制构件的承载能力;破坏形态的改变直接影响着构件的变形性能,随着剪跨比的增加,构件变形性能不断提高,且提高较快。
3.4 配箍率对抗剪性能的影响
保持轴压比、剪跨比、肢高厚比等截面参数不变, Z形截面柱在不同配箍条件下的抗剪性能计算结果见表7。配箍率与构件抗剪承载力及变形性能关系的曲线分别见图7、图8。
从图7可见:抗剪承载力一直呈上升状,且配箍率较小(ρsv≤0.3)时曲线上升较快,配箍率较大(ρsv>0.3)时曲线上升放缓。因此,从配箍对抗剪承载力的贡献角度分析,工程设计较合理的配箍率取值为0.3%。
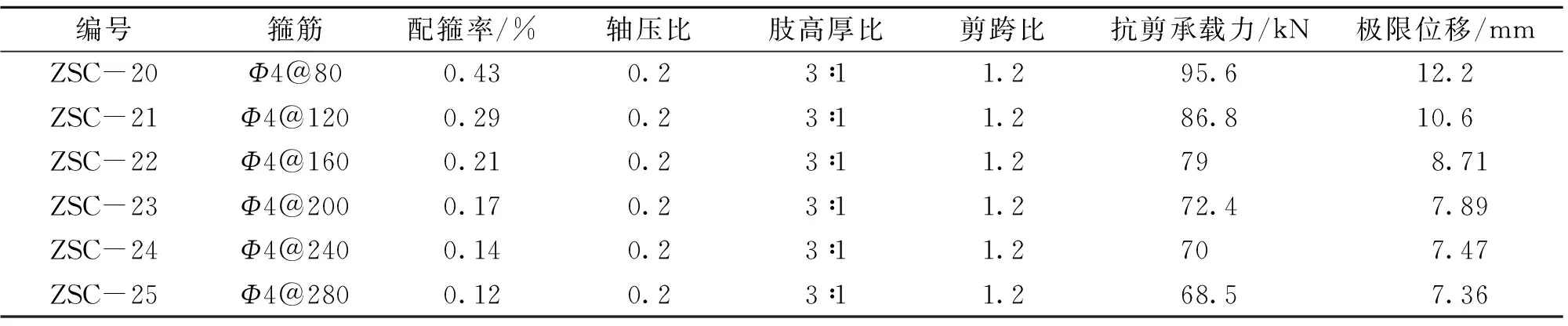
表7 配箍率对抗剪性能的影响
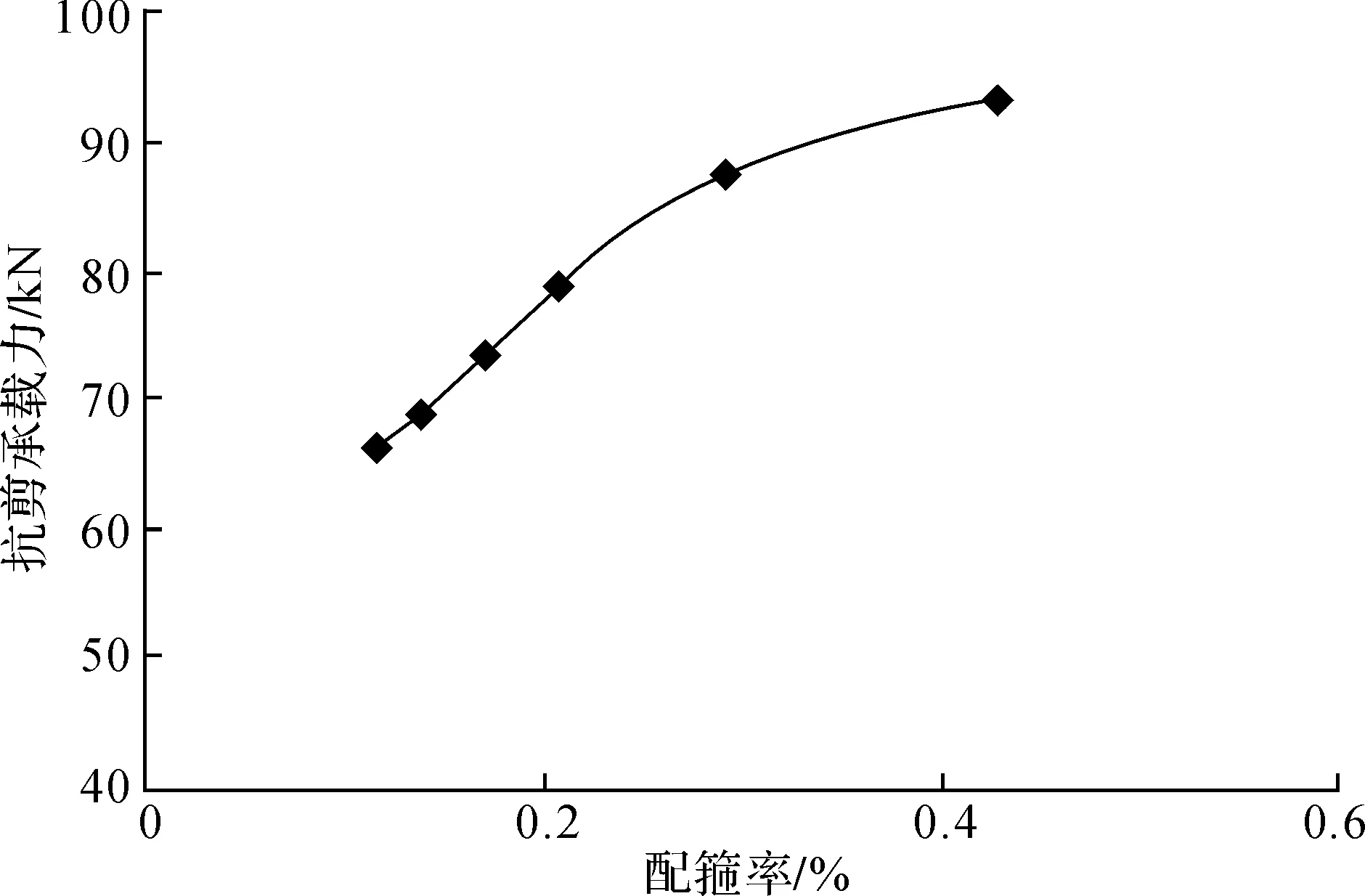
图7 配箍率与抗剪承载力关系图
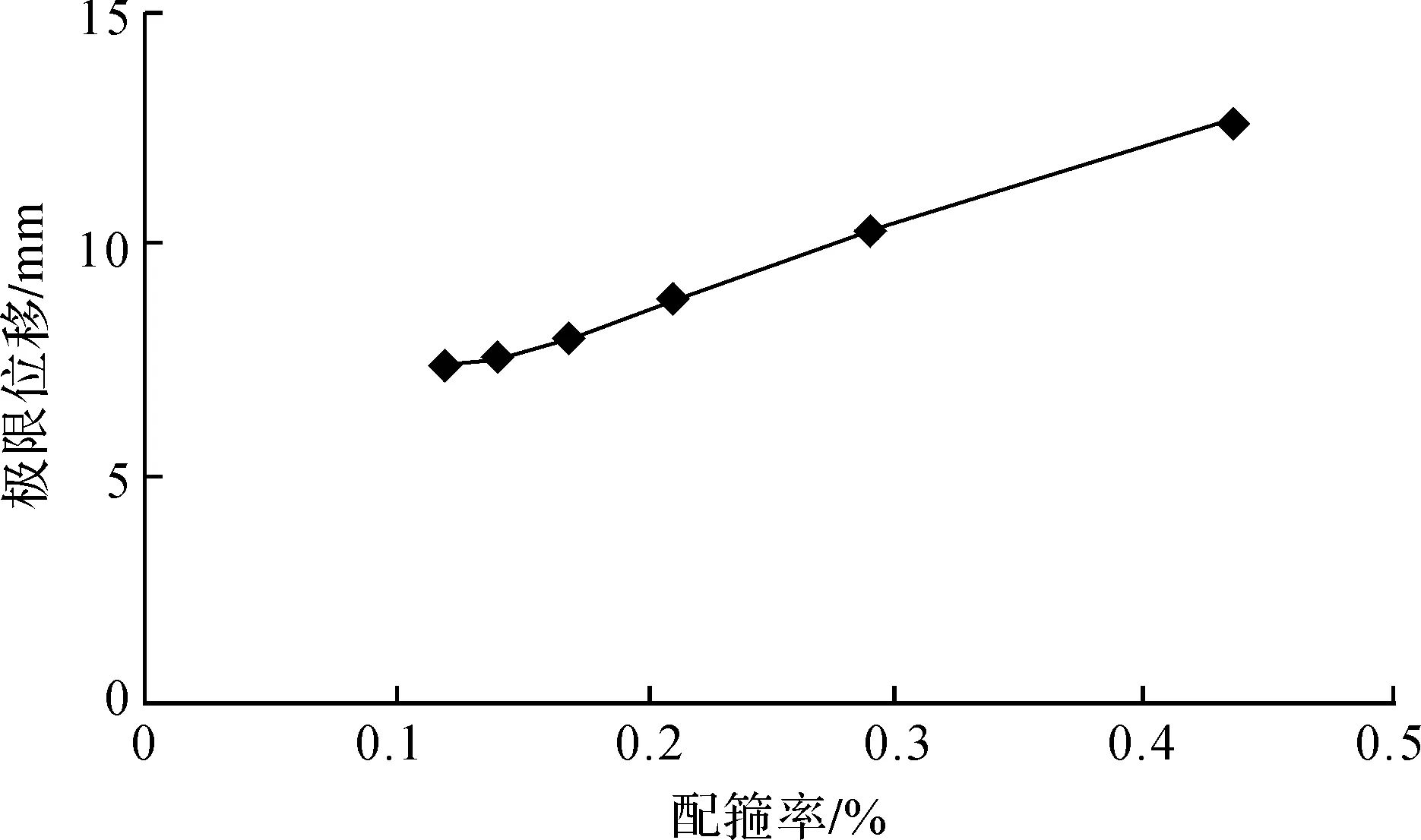
图8 配箍率与极限位移关系图
从图8的配箍率与极限位移关系图分析,随着配箍率的增加,Z形柱的极限变形量也一直呈上升状,且配箍率较小时曲线上升较慢,配箍率较大时曲线上升加快。这表明:当配箍率较小时,增加Z形截面柱的配箍,虽然能够改善构件的变形性能,但改善幅度相对较小。如果继续增加Z形截面柱箍筋数量,构件变形性能将大为改善。
4 结 语
通过对不同截面参数的25根Z形截面柱进行有限元数值仿真分析和受力机理研究,取得了以下几个方面的主要成果:
1)通过正确选择有限元单元类型、单元参数以及混凝土的应力-应变关系模型,可以得到与试验结果吻合较好的有限元模型,且利用此类模型来模拟Z形截面柱的抗剪性能是合理的,可以弥补试验在参数变化较少及试件数量较少方面的不足。
2)轴压比对Z形截面柱抗剪性能影响较大,当轴压比在0~0.4范围之内时,轴向压力的增加对抗剪承载能力的提高有较大贡献,当轴压比在0.4~0.6范围之内时,轴向压力增加对抗剪承载力的提高贡献相对减小。当轴压比大于0.6时,继续增加轴向压力,抗剪承载力将出现下降趋势,工程设计应将轴压比控制在0.4以下为宜。
3)轴压比是构件变形性能的重要决定因素。构件的变形性能随轴压比的增加而降低,轴压比较小(<0.5)时随着轴压比增加变形性能的下降较慢,轴压比较大 (>0.5)时,变形性能随着轴压比增加快速下降,会明显降低结构的抗震性能,故不论从Z形截面柱的抗剪承载力还是从变形性能而言,将轴压比控制在0.4以下是可靠的。
4)极限抗剪承载力随着剪跨比的增加而减小,但其减小幅度随剪跨比的增加而降低。剪跨比还决定了Z形截面柱的破坏形态,当剪跨比较小时(λ≤2)Z形截面柱容易产生剪切破坏,随着剪跨比的增加,构件破坏形态中的弯曲成分不断增加,直至弯曲型破坏控制构件的承载能力。破坏形态的改变进而影响着构件变形性能,随着剪跨比的增加构件变形性能不断提高。从结构抗震要求而言,将柱截面的破坏控制在弯曲破坏比较有利,而一般Z形截面柱的剪跨比也较大,故在工程设计中应重点配置有效的纵向钢筋。
5)Z形截面柱配箍率的提高有助于改善其极限抗剪承载力和变形性能,并且,当配箍较小时增加配箍对构件极限抗剪承载力的提高比较显著;当配箍率较大时增加构件配箍对极限抗剪承载力的影响减小,但对变形性能的改善非常显著,工程设计中配箍率取值0.3%为宜。
[1] 李杰,吴建营,周德源,等.L形和Z形宽肢异形柱低周反复荷载试验研究[J].建筑结构学报,2002,23(1):9-15.
[2] 毛晓飞,杨俊杰,蒋莉,等. 不同轴压比条件下Z形截面柱受剪性能试验研究[J].浙江工业大学学报,2009(2):221-225.
[3] 曹万林,黄选明,田宝发,等. 带暗柱Z形短柱抗震性能试验研究[J].世界地震工程,2003,19(2):45-50.
[4] 毛晓飞,杨俊杰,张柱. Z形截面柱抗剪性能试验研究[J].工业建筑,2010(8):9-15.

