基于遗传算法的地铁车站引导标识布点探析

穆瑞杰

(河南牧业经济学院 工程管理学院， 河南 郑州 450011)

0 引言

地铁车站大部分位于地下封闭空间，由于地下空间的特殊性，乘客对方向的感知和判断能力会减弱，容易迷失方向而导致寻路困难.因此，科学合理的引导标识能提高乘客的乘车效率，减少车站工作人员的劳动强度.

引导标识的设置问题一直是学术界比较关注的问题.Ichirow[1]从人性、需求方面对日本地铁站的乘客引导标识内容进行研究；安德烈亚斯·于贝勒等[2]通过引导标识的设计，分析总结出了一套全面性的方案，以保证运营的效率；Thompson[3]定性地指出机场引导标识设置需考虑空间环境和旅客特征；王丹[4]分析了导向标识的设置原则，并从人机工程学的角度定量地分析标识设置的要素； 陈霜霜[5]提出了基于人的视觉特性的导向标识，作为指导导向标识设计的理论基础.从以往的研究中可以看出，引导标识布点问题多为经验型的定性分析,但也存在利用数学模型求解的定量分析.韩艳欣等[6]针对大型客运站旅客向导标识布设的复杂性,提出基于遗传算法求解决策点的优化方法,并以北京南站为例进行标识布设实例分析,为实际方案的实施提供决策参考依据；张蛰等[7]提出了基于信息熵理论的标识引导服务效能计算方法，以导向标识协同服务效能最大为目标，建立导向标识布局优化模型，有效地提升了导向标识系统的服务效能.本研究将遗传算法首次应用于地铁车站乘客引导标识的布点问题，以获取地铁车站引导标识系统更为合理的布点，为地铁新开线路地下车站引导标识布点方案的选择以及现有车站引导标识系统的布点优化提供参考.

1 布点方法的选择

目前，地铁引导标识的布点多是根据经验设置的，缺乏科学依据，一旦投入使用，后期变更耗资巨大，因此，需要一种定量布点的方法.

遗传算法作为一种智能优化方法，具有较强的通用性，适用于多目标求解的问题，可用于解决方案优化和搜索问题，这与本研究目的一致.基于此，笔者运用遗传算法，解决引导标识的布点问题.

2 遗传算法的概述及实施

2.1 遗传算法概述

1967年，Holland的学生Bagley首次提出“遗传算法”.1975 年美国De Jong博士建立了遗传算法的工作框架[8]，并提出新的遗传算法操作技术. 1983年，Goldberg 将遗传算法应用于管道煤气系统的优化[9].另外，国内的一些学者如华东师范大学的姜昌华博士将遗传算法应用于物流系统的优化[10]，西南交通大学李梦潇、中国铁道科学研究院石振东将遗传算法应用于大型铁路客运站旅客引导标识设置[11-12].遗传算法是通过遗传和变异而形成的一种概率搜索方法.它的操作分为以下步骤.第一：建立初始种群.它需要给其准备一些表示起始搜索点的初始群体数据.种群数的规模N表示每一代种群中所含的个体数目.此次研究N的取值为200.第二：适应度函数设计.度量个体适应度的函数称为适应度函数fi，fi值越大，个体遗传到下一代的概率就越大，由于笔者是寻找乘客诱导量最大的个体，因此，诱导量越大也就是个体的适应度fi就越好，设置的引导标识就越有效.第三：遗传操作.首先，进行选择操作.设置n个群体，群体中个体i被选中概率设为pi，其适应度设为fi.其次，进行单点交叉操作.随机生成交叉点，在该处将配对个体进行交换. 最后进行变异操作.设变异概率Pm，若Pm值较大，必然会引起整个搜索空间的跳跃，若较小，又过于集中于局部.因此，本研究Pm取值0.008.

2.2 遗传算法的实施

遗传算法关键就是确定目标函数即引导标识对乘客诱导量最大，另外应根据车站具体设计情况和设计标准，设置一些约束条件[13].

车站引导标识建立适应度函数(乘客诱导量最大)可表示为：

(1)

式中：j代表引导标识的备选点，即决策点,j=1，2，…，m；i代表目标点，i=1，2，…，n；f(j)为决策量，当设置决策点时，f(j)=1，否则，f(j)=0；aji为分配系数，目标点i受决策点j服务时，aji=1，否则aji=0；α为权重系数，指诱导客流量与距离之间的平衡关系；dji为从标识点j到目标点i所经历的交叉点数量的倒数，该值越大，离目标点越近，反映的信息量就越大.

约束目标函数的条件.

(1)设置引导标识的数量p.

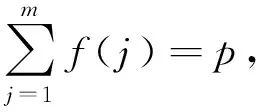
(2)

式中：j=1，2，…m.

(2)所有的客流均被诱导一次，对任意一个进站或出站线流均有：

(3)

式中：r表示进入站房客流数；Ir为第r股客流进、出站经过的候选点的集合.

(3)所有的目标点至少被经历过一次：

(4)

式中：i表示目标点的序号；Ii表示第i个目标前经历的候选点的集合.

3 引导标识布点案例

五一公园站是郑州地铁1号线的一个中间站，是地下二层车站.在调查过程中发现五一公园站乘客引导标识持续性比较差，布点不够科学合理，对乘客的引导作用有限.拟根据上述的遗传算法，找出合理的布点，使总的诱导量最大，从某种义上说，它是个复杂的决策点优化问题. 该问题属于多目标函数范畴，解决多目标函数方法有粒子群算法，多目标进化算法等[14-15]，此次选择的是遗传算法.

3.1 进站流线和流量

在五一公园站进行实地调查，得到车站半小时的客流量，图1是五一公园站进站流线和流量图.

图1中找出备选点j、aji、wji、dji，具体数据如表1，其中wji为通过现场客流调查获得.

按照式(1)，设计目标函数：

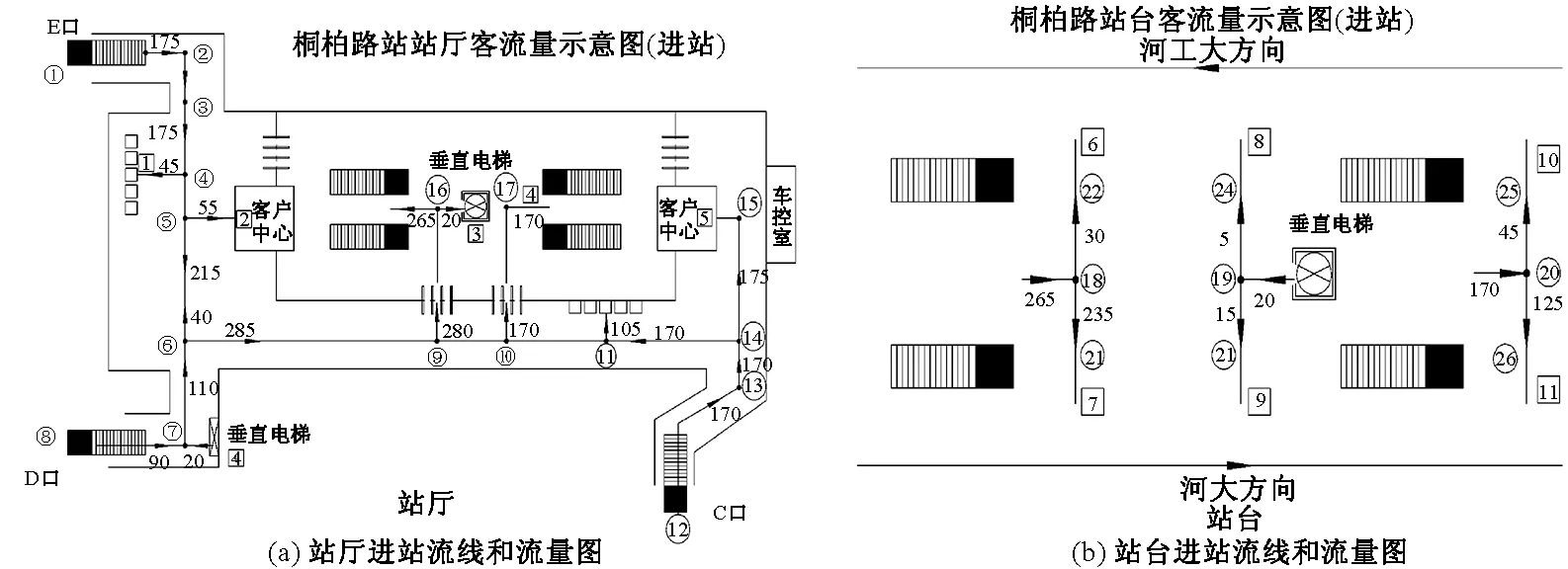
图1 站厅和站台进站流线和流程图Fig.1 The flow line and flow chart of the intake and platform

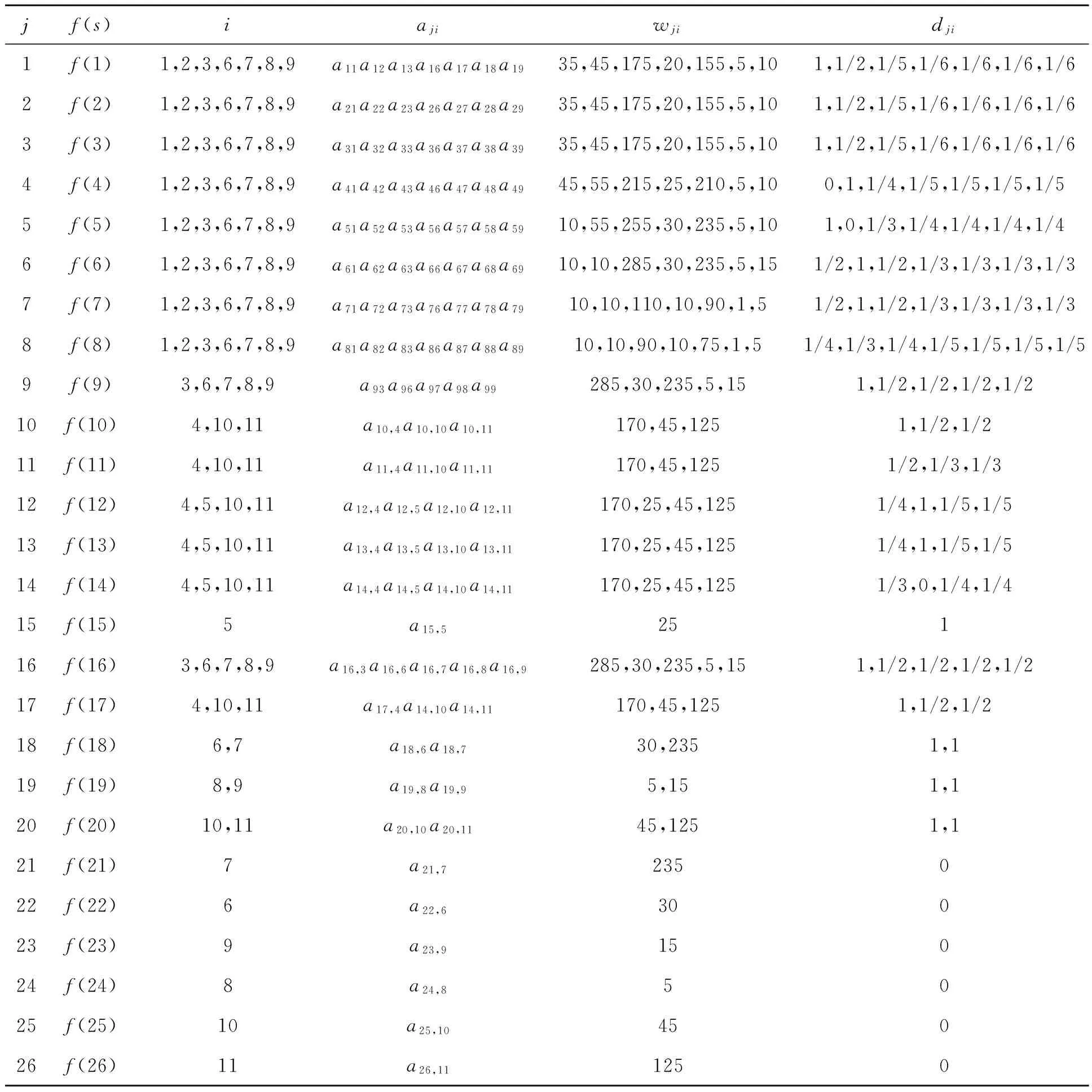
jf(s)iajiwjidji1f(1)1,2,3,6,7,8,9a11a12a13a16a17a18a1935,45,175,20,155,5,101,1/2,1/5,1/6,1/6,1/6,1/62f(2)1,2,3,6,7,8,9a21a22a23a26a27a28a2935,45,175,20,155,5,101,1/2,1/5,1/6,1/6,1/6,1/63f(3)1,2,3,6,7,8,9a31a32a33a36a37a38a3935,45,175,20,155,5,101,1/2,1/5,1/6,1/6,1/6,1/64f(4)1,2,3,6,7,8,9a41a42a43a46a47a48a4945,55,215,25,210,5,100,1,1/4,1/5,1/5,1/5,1/55f(5)1,2,3,6,7,8,9a51a52a53a56a57a58a5910,55,255,30,235,5,101,0,1/3,1/4,1/4,1/4,1/46f(6)1,2,3,6,7,8,9a61a62a63a66a67a68a6910,10,285,30,235,5,151/2,1,1/2,1/3,1/3,1/3,1/37f(7)1,2,3,6,7,8,9a71a72a73a76a77a78a7910,10,110,10,90,1,51/2,1,1/2,1/3,1/3,1/3,1/38f(8)1,2,3,6,7,8,9a81a82a83a86a87a88a8910,10,90,10,75,1,51/4,1/3,1/4,1/5,1/5,1/5,1/59f(9)3,6,7,8,9a93a96a97a98a99285,30,235,5,151,1/2,1/2,1/2,1/210f(10)4,10,11a10,4a10,10a10,11170,45,1251,1/2,1/211f(11)4,10,11a11,4a11,10a11,11170,45,1251/2,1/3,1/312f(12)4,5,10,11a12,4a12,5a12,10a12,11170,25,45,1251/4,1,1/5,1/513f(13)4,5,10,11a13,4a13,5a13,10a13,11170,25,45,1251/4,1,1/5,1/514f(14)4,5,10,11a14,4a14,5a14,10a14,11170,25,45,1251/3,0,1/4,1/415f(15)5a15,525116f(16)3,6,7,8,9a16,3a16,6a16,7a16,8a16,9285,30,235,5,151,1/2,1/2,1/2,1/217f(17)4,10,11a17,4a14,10a14,11170,45,1251,1/2,1/218f(18)6,7a18,6a18,730,2351,119f(19)8,9a19,8a19,95,151,120f(20)10,11a20,10a20,1145,1251,121f(21)7a21,7235022f(22)6a22,630023f(23)9a23,915024f(24)8a24,85025f(25)10a25,1045026f(26)11a26,111250

式中：α取值为1.5.

按照式(2)，设置引导标识数量p=16.按照式(3)，有f(5)+f(6)+f(7)>0,f(15)+f(14)+f(13)>0，f(4)+f(5)+f(6)>0.按照式(4),有f(3)+f(4)+f(5)>0，f(9)+f(16)>0，f(10)+f(17)>0，f(14)+f(15)>0，f(22)+f(18)+f(21)>0，f(19)+f(23)+f(24)>0，f(20)+f(25)+f(26)>0.

按照《公共信息导向系统国家标准》设计标准要求[13]，另增加的约束条件有：

f(4)=1，f(6)=1，f(14)=1，f(3)=1，f(1)=1，f(8)=1，f(12)=1.

为得到较为理想的结果，设计的参数值如下：染色体的数量为26个，总群种数200个，交叉率0.6，变异率为0.008，迭代次数100次.为提高计算效率，对遗传算法的计算过程采用VB编程计算.

由于遗传算法本身具有随机性，为体现算法的稳定性，对进站算法运行30次，分别记录30次的结果，并计算它们的均值和标准差，30次适应度值的均值为39 348.15，标准差为299.18，结果显示标准差在合理范围，证明该算法稳定性较好，选取了与适应度最大的值39 595.466 065 877 3，该值对应的群体最优解为10 111 101 111 101 011 111 000 000.

结合图1，可以得出算法计算的标志点应在1、3、4、5、6、8、9、10、11、12、14、16、17、18、19、20.本次选择的方案，在流线的交叉处如3、6、14等处增加进站乘车的标识，在乘客使用的设备处如4、9、10、11等处增加了设备使用的引导标识，在服务窗口如5、15处增加客服的引导标识，这些布点符合《公共信息导向系统》设计标准，满足乘客获取连续信息，办理进站手续的需要，同时确保最大客流诱导量，使引导标识作用最大.

3.2 出站流线和流量

图2是五一公园站出站流线和流量图.图2中找出候选点j、aji、wji、dji，具体数据如表2.其中wji通过现场客流调查获得.

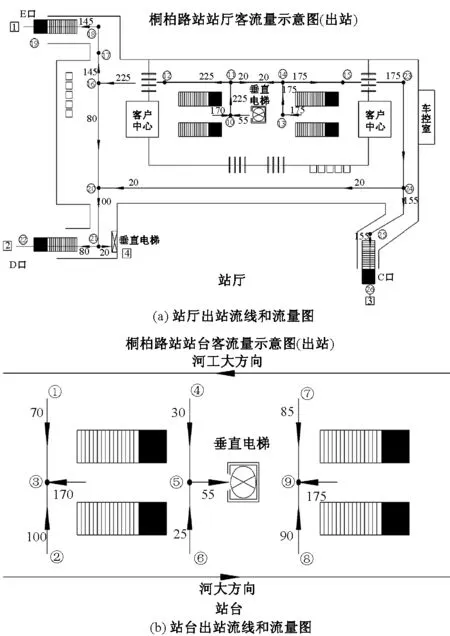
图2 站厅和站台出站流线和流量图Fig.2 The flow line and flow chart of out of the station and the platform

按照式(1)，设计目标函数：

式中:α取值为1.5.

按照式(2)，设置引导标识数量p=18.按照式(3)，有：f(1)+f(2)+f(3)>0，f(4)+f(5)+f(6)>0，f(7)+f(8)+f(9)>0.按照(4)式有：

f(16)+f(17)+f(18)+f(19)>0，f(16)+f(20)+f(21)+f(22)>0，f(23)+f(24)+f(25)+f(26)>0，f(16)+f(20)+f(21)>0.

按照《公共信息导向系统国家标准》设计标准要求[13]，另增加的约束条件：

f(16)=1，f(11)=1，f(14)=1，f(24)=1，f(20)=1，f(18)=1，f(25)=1.

为得到较为理想结果，设计的参数值如下：染色体的数量为26个，总群种数为200，交叉率为0.6，变异率为0.008，迭代次数为100次.笔者为提高计算的效率，对出站遗传算法的计算过程使用VB进行编程计算.

与进站算法一样，同样运行并记录了30次出站算法的运行结果，同时计算它们的均值和标准差，30次适应度值的均值为13 515.49，标准差47.23，结果显示标准差在合理范围，证明该算法稳定性较好，选取较好的适应度13 520.665 681 345 9，该值对应群体最优解为11 101 000 111 111 110 101 101 110.

结合图2，可以看出算法计算标识点应在1、2、3、5、9、10、11、12、13、14、15、16、18、20、21、23、24、25.本次设计的布点在流线的交叉点处设置引导标识，如11、14、16、20、24等处增加出站引导标识，在出站流线上如12、15处增加出站检票的引导标识，这完全符合乘客获取连续信息，办理出站手续的需要，提高出站流速，同时这些布点对客流的诱导量也较大，充分发挥引导标识的作用.

4 结论

笔者利用遗传算法获取科学、合理的乘客引导标识布点，实现了从定性分析转变为定量分析的跨越.它不仅开拓了引导标识布点优化思路，而且还为地铁车站设置引导标识提供了理论依据.笔者通过遗传算法寻找引导标识的布点，布点的位置与目前经验型设置的标识点重复率达到80%，但剩余20%的布点设置则更合理，是一种科学的优化.但算法也存在一定的局限性，如遗传算法实施过程中采用轮盘赌的方式选择个体，每次迭代完成后，都会出现一个最优结果，每次迭代的结果都会稍微有些差异.此次采用多次计算以提高布点位置的合理性.

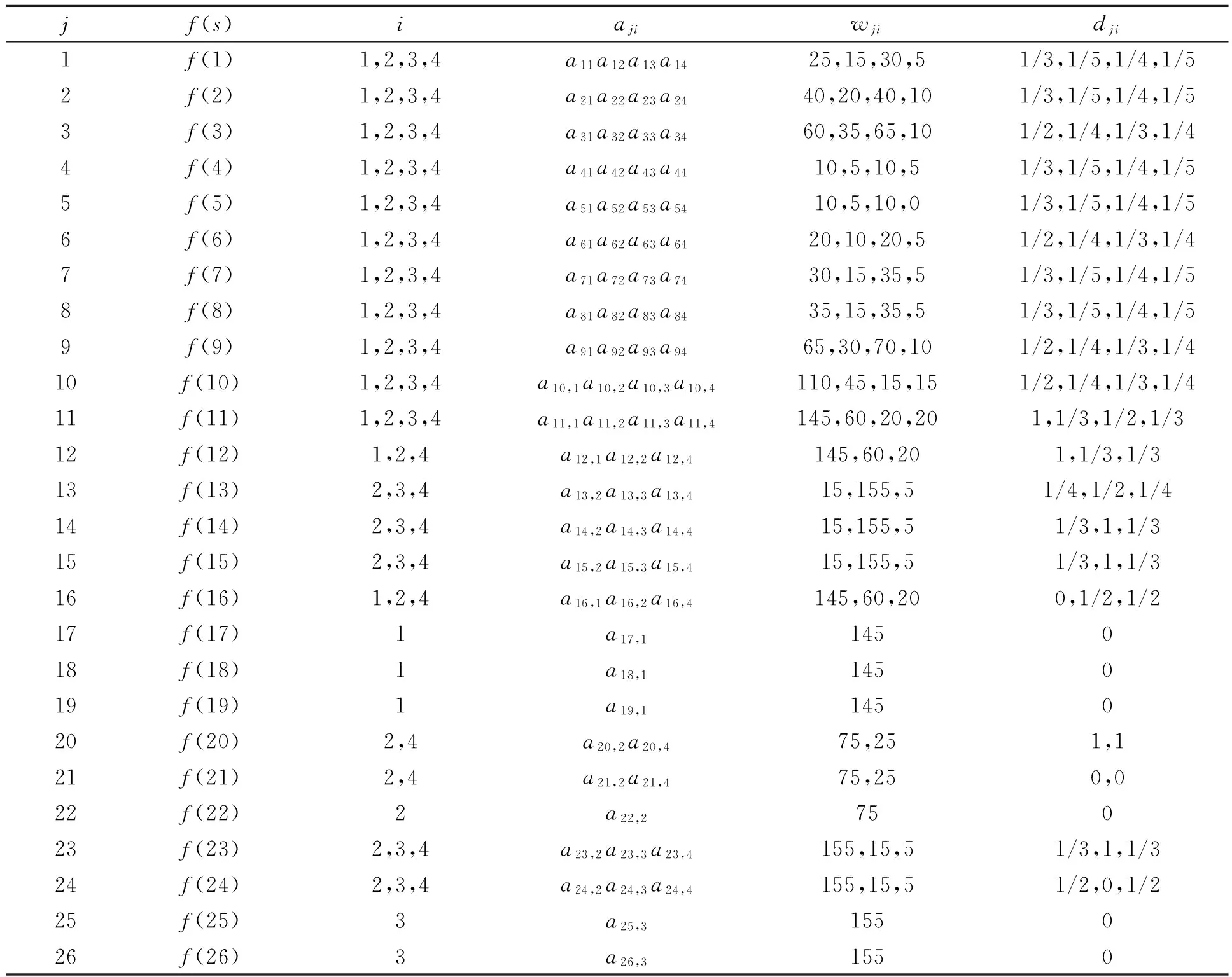
表2 出站参数

[1] ICHIRO W. Stanardized guide signs at yokohama station [J].Japanese railway engineering,2005, 45(3):16-18.

[2] 安德烈亚斯·于贝斯,高毅.导向系统设计[M].北京：中国青年出版社, 2008.

[3] THOMPSON N. Way finding and airport terminal design[J].The journal of navigation, 2009, 54(2): 177-184.

[4] 王丹.基于人机工程的铁路车站引导标识系统分析[J].四川建筑,2010,30(2):65-68.

[5] 陈霜霜.基于人的视觉特性的标识设计研究[D].上海：东华大学机械工程学院,2014.

[6] 韩艳欣,张喜.基于遗传算法的车站标识决策点布设方法研究[J].铁路计算机应用,2009,18(11):10-13.

[7] 张蛰,贾利民,秦勇.基于协同引导的地铁站台导向标识系统布局优化[J].交通运输系统工程与信息,2016,16(4):146-152.

[8] DE JONG K A.An analysis of the Behavior of a class of genetic adaptive systems[M].Michigan:University of Michigan Press, 1975.

[9] GOLDBERG D E.Genetic algorithms in search, optimization, and machine learning[M]. USA:Addsin-wesley Publishing Company,1989.

[10] 姜昌华.遗传算法在物流系统优化中的应用[D].上海：华东师范大学信息科学技术学院,2007.

[11] 李梦潇.大型铁路客运站旅客引导标识合理设置研究[D].成都：西南交通大学交通运输与物流学院,2011.

[12] 石振东.新唐山站旅客引导标识系统设计研究[D].北京：中国铁道科学研究院运输及经济研究所,2016.

[13] 全国图形符号标准化技术委员会,中国标准出版社.公共信息导向系统国家标准汇编[M].北京：中国标准出版社，2015.

[14] 瞿博阳,刘丁明,乔百豪,等.粒子群算法及其改进研究[J].自动化应用,2016,57(11):49-51.

[15] 肖俊明,周谦,瞿博阳,等.多目标进化算法及其在电力环境经济调度中的应用综述[J].郑州大学学报(工学版),2016,37(2):1-9.