均衡策略粒子群算法在图像分割中的应用

夏星宇， 高 浩， 王创业

(1.南京邮电大学 自动化学院，江苏 南京 210046; 2.安徽省蚌埠市供电局，安徽 蚌埠 233000)

0 引言

图像分割的目的是将一幅图像划分成有意义的区域或部分，其中每部分区域具有相似的特征.近几年来，学者们提出了很多较为有效的图像分割技术[1].它们大致可以分为两类：一类是利用图像的灰度直方图，通过其特征来决定分割的最佳阈值[2].另一类是构造一个适应度函数，通过优化适应值函数来决定最优的阈值，如基于熵的阈值分割技术,贝叶斯误差最小化等.这些技术在医学图像、人脸识别、计算机视觉等领域已经取得了不错的效果.然而，其中的一些方法计算非常耗时，如Kapur和Otsu算法[3-4]的运算时间相当长，且随着阈值数目的增加运算时间呈指数增长，其穷举的搜索策略限制了它在处理实际多阈值问题中的应用.

近年来，为缩短运算时间，研究人员已经成功地将很多优化算法引入到阈值图像分割中来.作为基于种群的优化策略，进化算法受自然界生物的启发，主要采用3个主要操作(选择、变异和交叉)来产生后代.由于有着运算速度快和全局搜索能力较强等特点，近几年，进化计算已经广泛地应用到了图像分割领域.Tao等[5]采用蚁群算法来优化基于熵的目标分割适应值函数，寻找最优的阈值.Yin等[6]提出一种改进的遗传算法来缩短多阈值分割的时间.Gao等[7]将粒子群优化算法引入到图像阈值分割领域，实验证明它可以取得和穷举搜索相近的实验结果.Yin[8]将基于协作策略的量子粒子群算法QPSO应用到图像分割中来，实验证明当处理同一分割问题时，该算法可以取得比其他同比优化算法更好的效果.

作为较为流行的进化算法之一，粒子群算法兼有进化计算和群智能的特点.与其他进化算法相类似，该算法模拟鸟群集体飞行觅食的行为，通过鸟之间的集体协作与竞争使群体达到目的.算法已经成功地应用到工业生产、模式识别、医学处理等多个领域[9-10].但由于粒子群算法具有早熟收敛的缺点，因此笔者提出一种基于均衡策略的粒子群算法(particle swarm optimization with an equilibrium strategy,EPSO)，在提出一个有价值的引导点的同时，合理地赋予粒子在全局和局部搜索的可能性，较好地均衡了算法的全局和局部搜索能力.同时把改进后的粒子群算法应用到基于Kapur最大熵图像分割中，有效地解决图像阈值分割耗时长这一问题.

1 粒子群进化算法

作为一种基于种群的进化算法，粒子群进化算法[11]操作简便，近年来，受到了广泛的关注.在粒子群中，固定规模的种群代表了一系列的可行解.每个备选解被称为一个“粒子”，多个粒子共存，合作寻优，近似鸟群寻找食物.算法先生成初始种群，即在可行解空间中随机初始化一群粒子，每个粒子都为优化问题的一个可行解，并由目标函数为之确定一个适应值.在每一次迭代过程中，粒子将跟踪两个极值，一个为粒子本身迄今找到的最优解Pp，另一为全种群迄今找到的最优解Pg.基本迭代公式为：

vid(t+1)=vid(t)+c1r1·(ppid-xid(t))+

c2r2·(pgd-xid(t))；

(1)

xid(t+1)=xid(t)+vid(t+1)，

(2)

式中：i=1,2,…,S；d=1,2,…,n；r1和r2是服从U(0,1)分布的随机数；学习因子c1和c2为非负常数，c1=c2=2；vid=[-vmax,vmax]，vmax是由用户设定的速度上限;ppid以及pgd分别代表个体最优和群体最优在第d维上的解.

2 基于均衡策略的粒子群算法

以往的研究成果表明，传统的粒子群算法具有早熟收敛的缺陷，为在保持粒子群算法收敛速度快的基础上提升算法的全局搜索能力，笔者提出了一种新方法.首先，为了在算法运行过程中一直能够为粒子群提供一个较大的搜索能力，使得粒子群能够保持跳出当前局部搜索区域的概率，笔者提出了一个均衡因子：

g=abs(r3(0,a1)/r4),

(3)

式中：r3为符合高斯分布的随机序列;r4是服从U(0，1)分布的随机数；a1为该高斯分布的标准差.实验结果表明,当a1为0.35时,改进后的粒子群算法能够取得较优的实验结果，并保证算法在迭代初期获得较强的全局搜索能力和在后期具有较优的局部搜索能力.

粒子群迭代公式：

xid(t+1)=Qd±α·g·(Pmd-xid(t)),

(4)

其中,Qd=r1·ppid+(1-r1)·pgd+r3·

(Pgd-round(Pgd)).

(5)

与以往算法不同的是式(5)不仅包含了文献[12]证明的粒子群收敛进化方向Qd=r1·ppid+(1-r1)·pgd，同时还给出了一个扰动因子r3·(pgd-round(pgd)).r1是服从[0,1]的均匀分布的随机数，r3是服从标准正态分布的随机数.这样不仅给粒子进化提供了一个有效的方向，同时能够保证个体在运行过程中特别是在ppid=pgd的情况下，通过借鉴群体历史最优解Pg的数值产生一个相对较小的值，给予个体一个较小的扰动，保证个体能够在局部区域进行有效搜索.

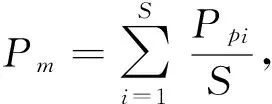
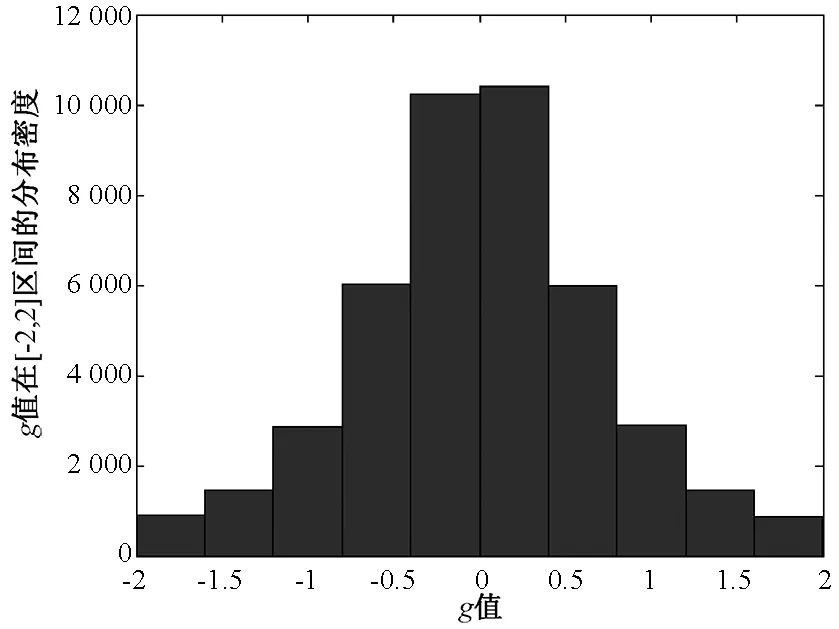
图1 g∈[-2,2]之间的分布图Fig.1 The distribution of g∈[-2,2]

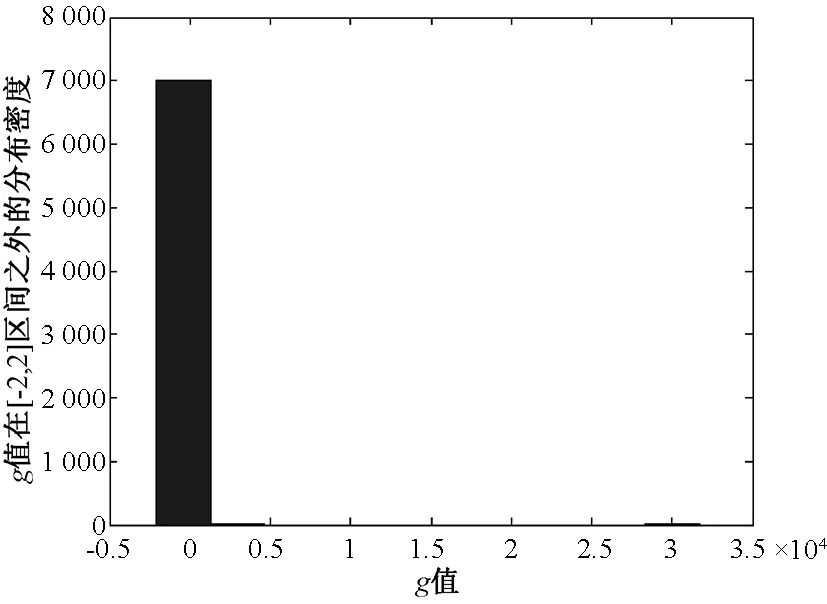
图2 g∉[-2,2]的分布图Fig.2 The distribution of g∉[-2,2]

通过对图1和PSO算法的c1以及c2比较，相对于c1以及c2的取值范围[-2,2]之间的均匀采样，很容易发现EPSO算法能够在[-1,1]之间产生更多的解(大致为40 000次)，从而能够在Qd确定的局部区域产生更为集中的解，这样就可以使得种群获得更多的局部搜索机会；而图2的结果表明相对于标准的PSO算法的c1以及c2的取值范围，EPSO能够产生数值更大的备选解，最大值可达到3.2×104，这就意味着种群在寻优过程中能够获得更多跳出局部最优解的能力.

EPSO算法步骤如下.

(1)依照初始化过程，对粒子群的随机位置和速度进行初始设定;

(2)计算每个粒子的适应值;

(3)对于每个粒子将其适应值与所经历过的最好位置Pp的适应值进行比较，若较好，则将其作为当前的最好位置;

(4)对于每个粒子将其适应值与全局所经历的最好位置的适应值进行比较，若最好，则将其作为当前的全局最好位置;

(5)根据方程(4)和方程(5)对粒子的速度和位置进行进化;

(6)如未达到结束条件通常为足够好的适应值或达到一个预设最大代数，则返回步骤(2).

3 对比试验

3.1 标准测试函数试验设计及结果

为了分析笔者提出的EPSO的总体性能，笔者设计了多种测试实验对PSO[12]、QPSO[13]、HRPSO[14]、HWPSO[15]、CCPSO[16]以及 EPSO进行了对比分析. 同时使用8个标准测试函数[11]问题来进行多方面考察和比对.笔者测试所有算法使用的个体总群个数都设为20(ABC算法根据算法流程个体总数设置为10).测试函数中f1-f3是单模函数，f4-f6是具有多个局部最小点的多模函数，函数的评估次数设置为2 000×测试函数维数.f7-f8是低维函数，函数的评估次数设置为10 000.所有测试函数的理论最优解均为0.最好的对比结果在表2和表4中加黑显示.

对于单模函数来说，由于EPSO使用了Qd点指引整个群体进行搜索，在整个粒子进化过程中一直给予粒子进化提供了一个有价值的方向，特别是当出现Ppd=Pgd的情况时，扰动因子依然能够提供给粒子在局部区域更多的搜索机会.相对于同样使用文献[10]提出收敛点的QPSO来说，由于EPSO算法使用了扰动因子，能够提供给粒子群体更多的局部搜索机会.另外，根据图2的实验结果，相对于传统的学习因子，EPSO算法的g因子能够在[-2, 2]局部范围内提供给粒子以更多的在小范围内搜索的机会，因此粒子可以在Q点定义的局部范围内进行精确搜索，从而在单模函数上获得较快和较为精确的解.对于复杂的多模函数，同其他比较算法相比，由于EPSO算法使用了均衡因子，使得个体能够获得更大的解，具有较强的跳出局部最小点的能力，从而提高了算法特别是在迭代后期搜索整个解空间的可能性.此外由于算法的局部搜索能力也较为优异，在全局和局部搜索能力上获得了较好的平衡，因此在多模函数上获得了更为精确和满意的结果.表1为标准测试函数，表2为各种比较算法在测试函数的比较结果.根据表2的研究结果表明，EPSO在低维函数上依然取得较优的结果.因此，可以得出结论，EPSO不仅在高维函数上，同时在低维函数上表现出了较优的搜索能力.

3.2 图像函数测试设计及结果分析

由Kapur提出的基于熵准则的图像分割方法由于可以针对基于直方图的图像提供良好的图像分割而得到了大量应用.传统的Kapur方法是基于双阈值的图像分割方法，近年来它已经被成功地应用到多阈值分割领域.具体描述如下.

f([t1,t2,…,tM-1])=H0+H1+…+HM-1；

(6)

(7)

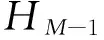
(8)

Pi=h(i)/N,

(9)

其中,N代表图像包含的像素个数;L=255表示最大的灰度级;h(i)表示的是在第i灰度级上图像像素的个数.在0～L间改变对应的各个阈值，求满足式(6)为最大值的{t1,t2,…,tM-1}，此时的{t1,t2,…,tM-1}便是最佳阈值.显然要得到arg max{f(t1,t2,…,tM-1)}，必须对区间所有的灰度值进行多级熵值计算，最后比较得到最大的熵值，其计算量较大，而且随着分割阈值数目的增加其时间复杂度为O(255M-1)，这将严重阻碍了Kapur方法的应用以及推广.为了减少标准Kapur算法的运算量，笔者利用EPSO快速收敛特性解决标准Kapur算法存在的这一难题.此外，为了验证EPSO算法的具体性能，笔者设计了5类比较试验：①ACO算法[17]；②GA-L算法[18]；③ABC算法[5]；④PSO算法[11]；⑤CQPSO[9]算法；⑥QPSO[13]算法；⑦EPSO算法.这些算法的参数设置都严格按照相对应的文献进行处理.所有算法的比较在Core 2 Duo 3.2GHZ电脑使用MATLAB语言完成.分割的阈值分别设为2、4、6，对应的函数评价次数为2 000.测试的图像分别采用比较算法中最常用的图像以及伯克利大学提供的标准测试图像，图3为示例图像.此外，由于标准Kapur算法在阈值数超过4以后的运算时间过长，因此只列出阈值数为2和4的结果.

表1 标准测试函数

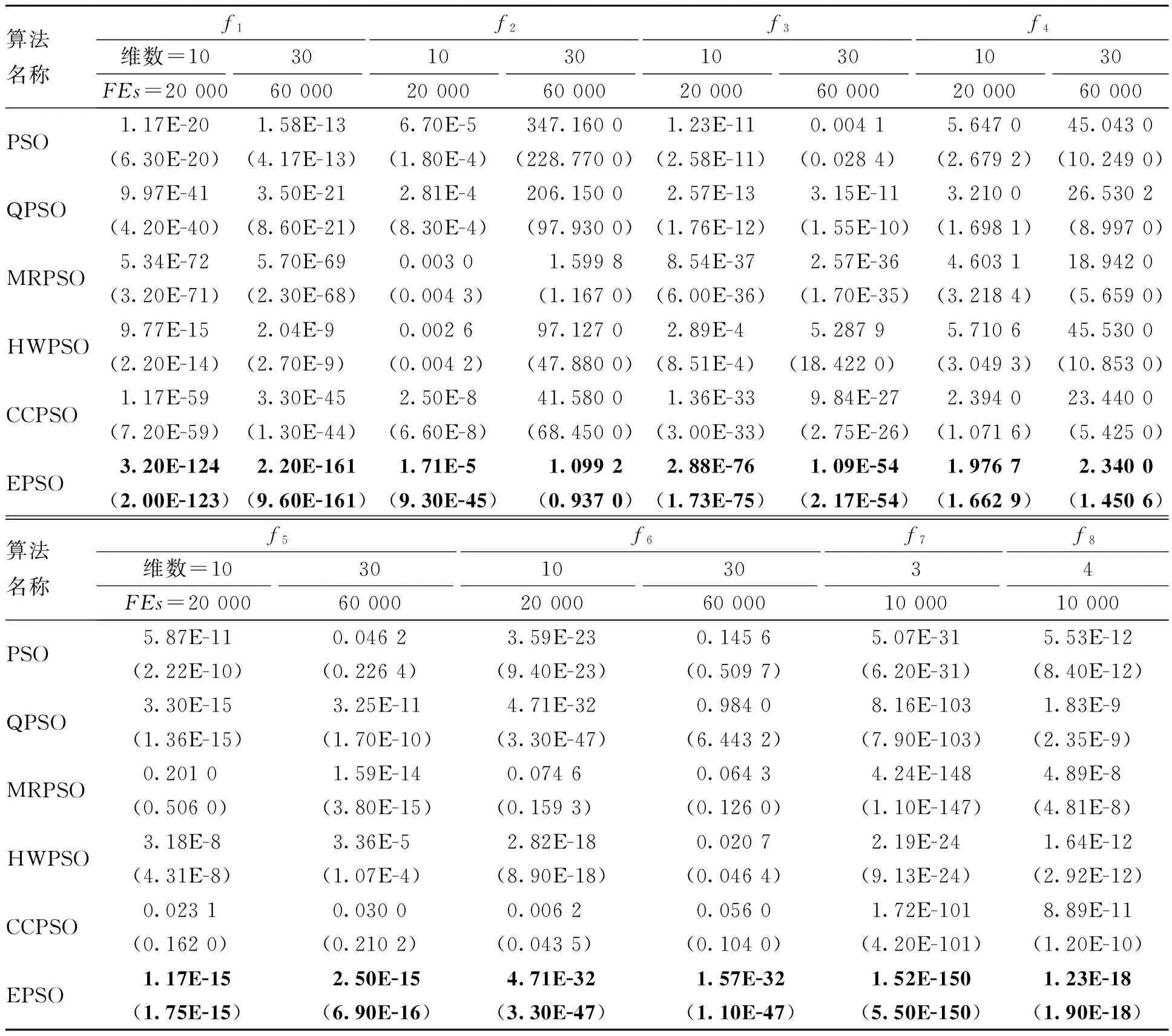
表2 各种比较算法在测试函数的比较结果(平均值(方差))Tab.2 The comparison results between different algorithm on benchmark functions (Mean values (Standard deviation))

图3 测试图像Fig.3 Tested images

从表3和4的结果可以看出，笔者提出的EPSO算法获得了与标准Kapur算法最为接近的适应度值，同时根据表3得到的结果，基于EPSO算法的Kapur分割方法所耗费的CPU时间随着阈值的增加并不特别明显，远远降低了标准Kapur算法的时间复杂度，因此，相对于标准算法，笔者提出的算法有效地提高了算法的运行效率.此外，如表4所示，与ABC、 ACO、PSO、CQPSO、GA、QPSO 6个基于进化算法的图像分割方法相比，EPSO在4幅图片上均取得了最佳的适应度值和方差，这主要是和各自算法的搜索策略有关.由于ABC算法采用单维的搜索策略，使得算法在每一维上都能够进行精细的搜索，保证了算法的可靠性.同时由于使用了贪婪搜索策略，能够给群体进化提供一个较优的方向，在全局和局部搜索能力上获得了较好的平衡，因此获得了较好的寻优结果.蚁群算法由于使用了信息素的概念，个体在寻优的过程中比遗传算法获得更多的借鉴群体最优解的机会，因此在比较的图像上获得比遗传算法更好的结果，但相对于其他群体算法，信息素的更新较为缓慢，因此在有限的迭代次数内分割效果差于其他的基于群体算法的分割方法.而遗传算法相对于其他比较算法来说，个体在寻优过程中只和父代进行经验交换，因此收敛速度最慢，在规定的时间内无法获得优异的成绩，效果最差.PSO以及QPSO算法虽然相对于其他进化算法有着收敛速度快的优点，但却易于陷入局部最优，因此虽然相对于GA和ACO算法来说获得较好的实验结果，但相对于ABC和改进的粒子群算法却成绩较差.CQPSO算法由于使用了协作策略，因此能够在一定程度上克服维数的束缚，在高维上(除去笔者提出的算法)获得了较好的试验结果.笔者提出的算法由于使用了均衡因子，在算法迭代过程中(特别是迭代后期)能够获得更多的在全局范围内搜索的机会，相对于PSO及其改进算法提升了全局搜索能力，从而能够保证最终获得解的可靠性.同时，由于算法仍然使用了群体和个体历史最优解的概念，因此继承了PSO算法收敛速度快的特点.此外，由于在搜索方向上引入了扰动因子，能够在算法迭代过程中不断地给予个体一个微动力，使得个体能够在局部范围内获得更多的搜索机会，因此具有搜索更为精确解的能力.图4给出了各种比较算法在Berkely标准图像分割测试库上测试获得的名次排名总和(越小越好)，EPSO算法相对于其他算法获得了最好的名次，同样验证了算法的有效性.结合表3所示结果，PSO和EPSO算法在2维和4维上的分割耗费的时间为同一量级，而分割效果远远优于PSO算法，进一步说明本方法改进的必要性.同时，对于标准方差这一考核指标，EPSO也取得了比其他5种算法更为优异的稳定性，这说明笔者所提出的优化算法在分割过程中更加稳定，鲁棒性好.图5为EPSO算法在示例图像阈值为6时的分割结果.整体而言，EPSO在整个测试图片4个阈值上都取得了最好的优化成绩和标准偏差，说明该算法可以取得更好的分割效果和更稳定的分割性能.

表3 标准Kapur、PSO、EPSO在示例图的比较结果

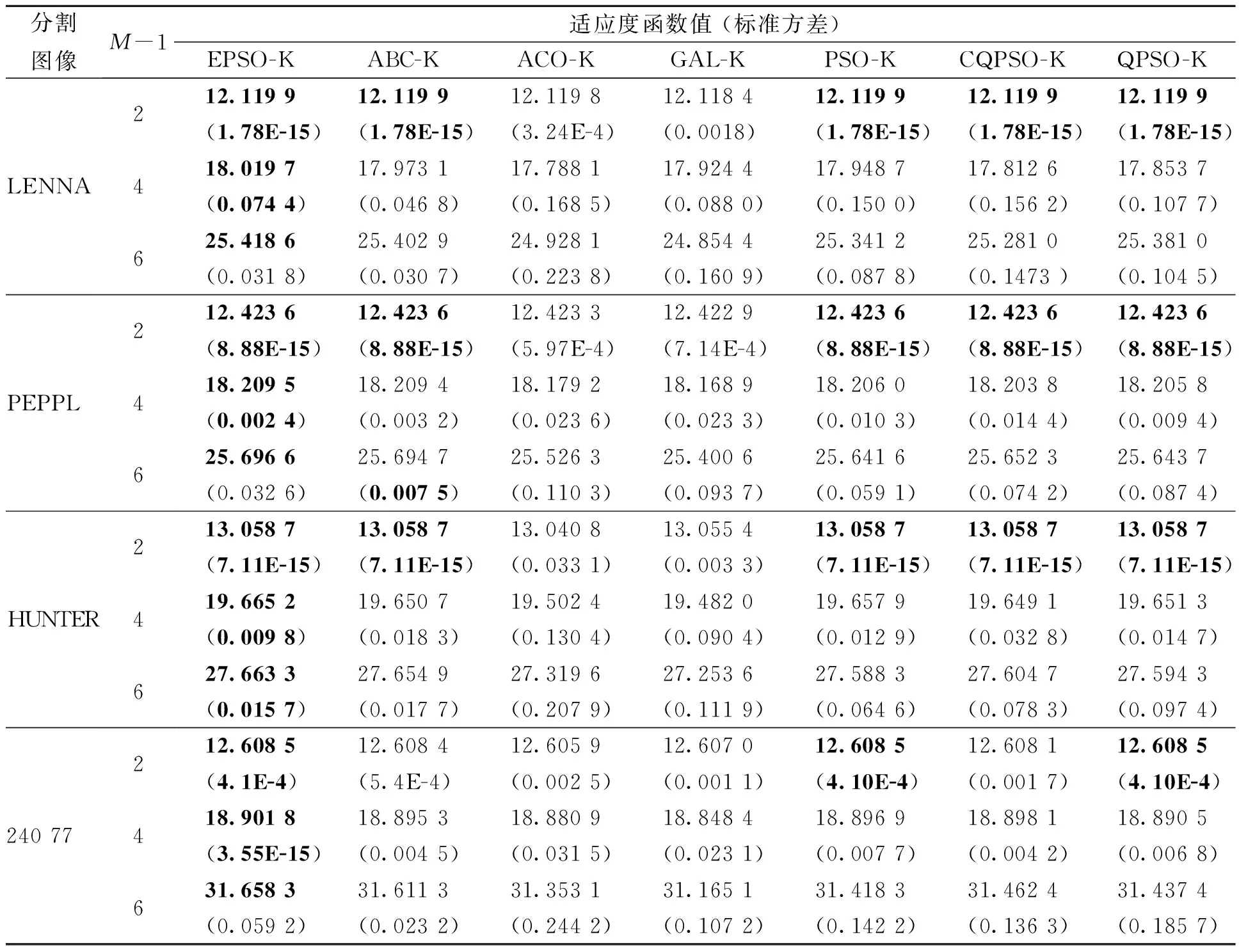
表4 基于进化算法的Kapur分割方法的比较结果

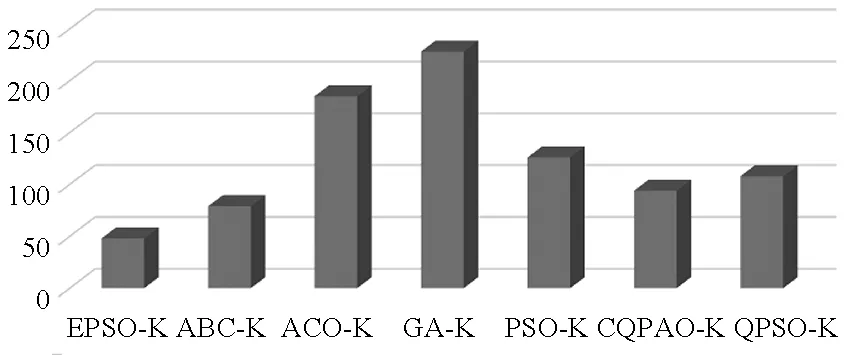
图4 基于进化算法的Kapur分割方法在Berkeley标准测试库测试的名次Fig.4 The ranking of EAs based Kapur algorithm on Berkeley image database

4 结论

笔者根据粒子群进化算法本身的特点，首先提出了一个新的均衡策略，使得算法可以在保证全局搜索能力的条件下加快收敛速度.然后在此基础上采用了一个新的引导个体，使得个体能够在局部范围内更为精确地搜索，从而得到更优的优化效果.改进算法在标准测试函数以及图像阈值分割中取得了比其他算法更好的成绩，从而证明了其有效性.以后的工作将继续关注如何在保证分割时间较短的情况下更高地提高算法的优化效果.

图5 EPSO在阈值为6时的分割图Fig.5 The segmented images with six thresholding by EPSO

[1] 王忠勇,贾萌,候中新,等.基于形态学特征的颗粒图像分割和计数[J]. 郑州大学学报(工学版), 2015, 36(2): 80-84.

[2] 刘松涛,殷福亮.基于图割的图像分割方法及其新进展[J]. 自动化学报, 2012, 38(6): 911-922.

[3] SAHOO P K, KAPUR J N, WONG A K C. A new method for gray-level picture thresholding using the entropy of the histogram[J]. Computer vision graphics image processing, 1985, 29(3): 273-285.

[4] OTSU N. A threshold selection method from gray-level histograms[J]. IEEE transactions on system, man and cybernetics, 1979, 9(1): 62-66.

[5] TAO W B, JIN H and LIU L M. Object segmentation using ant colony optimization algorithm and fuzzy entropy[J]. Pattern recognition letter，2007, 28 (7): 788-796.

[6] YIN P Y, CHEN L H. A fast iterative scheme for multilevel thresholding methods [J]. Signal process, 1997, 60 (3): 305-313.

[7] GAO W F, LIU S Y, HUANG L L. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning [J]. IEEE transactions on cybernetics, 2013, 43(3), 1011-1024.

[8] YIN P Y. Multilevel minimum cross entropy threshold selection based on particle swarm optimization [J]. Applied mathematics and computation, 2007, 184 (2): 503-513.

[9] GAO H, XU W, SUN J, et al. Multilevel thresholding for image segmentation through an improved quantum-behaved particle swarm algorithm [J]. IEEE transactions on instrumentation and measurement, 2010, 59 (4): 934-946.

[10] 朱晓东,刘丹,李广.基于混合优化算法的模糊系统辨识[J]. 郑州大学学报(工学版), 2015, 36(4): 10-14.

[11] KENNEDY J, BLACKWELL T. Particle swarm optimization [J]. Swarm intelligence, 2007, 1(1):33-57.

[12] CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multi-dimensional complex space [J]. IEEE transactions on evolutionary computation, 2002, 6(1): 58-73.

[13] SUN J, FENG B, XU W. Particle swarm optimization with particle having quantum behavior [C]// Congress on Evolutionary Computation. Portland, OR:IEEE Press, 2004: 325-331.

[14] GAO H, XU W B. A new particle swarm optimization and its globally convergent modifications [J]. IEEE transactions on system, man, and cybernetics, Part B, 2011, 41(5): 1334-1351.

[15] LING S H, IU H H C, CHAN K Y, et al. Hybrid particle swarm optimization with wavelet mutation and its industrial applications [J]. IEEE transactions on system, man and cybernetics, Part B, 2008, 38(3): 743-763.

[16] PARK J B, JEONG Y W, SHIN J R, et al. An improved particle swarm optimization for nonconvex economic dispatch problems[J]. IEEE transaction on power systems, 2010, 25(1): 156-166.

[17] AKAY B. A study on particle swarm optimization and artificial bee colony algorithms for multilevel thresholding [J]. Applied soft computing, 2012, 13(6): 3066-3091.

[18] CAO L, BAO P, SHI Z K. The strongest schema learning GA and its application to multilevel thresholding [J]. Image vision computing, 2008, 26(5): 716-724.