基于相交道路左转饱和交通量的MULTIBAND改进模型

常玉林， 郑献予， 张 鹏

(1.江苏大学 汽车与交通工程学院，江苏 镇江 212013； 2.东南大学 城市智能交通江苏省重点实验室，江苏 南京 211189)

0 引言

干线因其较大的基本通行能力和较高的通达性成为很多驾驶员的首选道路，因此干线的畅通对于城市路网的畅通至关重要.干线协调控制以干道上各交叉口的交通量大小为依据，通过设置合理的相位差减少车辆在干道上的延误和停车次数，提高了干道的实际通行能力. 干线协调控制的策略之一是使绿波带宽最大，MAXBAND模型由Morgan等[1]提出，以最大绿波带宽为目标，使用混合整数线性规划方法得出恒定绿波带宽下的全局最优解，是干线协调控制中经典模型之一. MULTIBAND模型[2]在此基础上根据路段上交通量的差异给出与之相协调的带宽，这种可变带宽的思想进一步提高了干线协调的控制效果. 自Gartner等[3]于1996年将MULTIBAND模型实际运用到干道的协调控制后，国内学者针对我国城市交通流特征作出很多本土化改进. 卢凯等[4]将绿波带宽分配影响因子和带宽需求比例系数引入模型的目标函数中；王世明等[5]则对主干道左转相序形式进行效益分析；陈宁宁等[6]将动态红灯排队消散时间模型融入干道双向绿波协调控制模型中；侯永芳[7]引入非协调相位的饱和度对非关键交叉口的绿灯时长进行优化分配；秦雅琴等[8]建立了以实际交叉口位置与理想交叉口位置偏差之和最小为优化目标的公共信号周期优化模型.

1 问题描述与改进对策分析

由于大部分与干道相交的道路为支路[9]，且相交道路汇入干道的交通量较为有限，大多数干线协调优化模型并不考虑相交道路经左转汇入干道的交通量. 然而干道上的一些主要交叉口相交道路左转流量较大，尤其在流量达到饱和时，大量的相交道路左转交通量在汇入干道后，若不处于绿波带宽范围内，行驶至下游第一个交叉口时需停车排队，较长的排队长度意味着下游交叉口的协调方向排队消散时间的增加，从而降低了干道协调在高峰期的控制效益.

为了解决上述问题，笔者将对相交道路左转交通流处于饱和状态时，协调方向出口道流量特征进行分析，并分别对相交道路左转相位的早闭和滞后于协调方向相位两种情况分别建模，通过仿真得出最佳绿波控制效果时的相序设置形式. 根据沈家军等[10]的研究成果，为确保交叉口的通行效率，交叉口配时采用含相交道路专用左转相位的四相位配时方案.

1.1 协调方向交叉口出口道交通量的变化特征

设交叉口右转车辆不受信号控制，交叉口信号周期为C，协调方向相位为G且为周期的第一相位，相交道路左转相位为L. 依据交叉口进口道的交通量变化特征[11]，不同相序设置方式使得周期内协调方向交叉口出口道交通量呈现出不同的变化特征.

当相交道路左转相位L先于协调相位G执行时，该相位为周期内的第四相位，周期内协调方向出口道交通量特征如图1所示.周期开始后，协调方向交叉口出口道交通量以相交道路左转进口道饱和流量为起始，迅速上升至协调方向进口道饱和流量，待排队车辆清空后，协调方向交通流逐渐转为自由流至相位G结束；在第四相位L被执行前，由于只有相交道路右转车辆允许进入协调方向出口道，此时协调方向交通流将从协调方向自由流转为相交道路右转的自由流直至第四相位L被执行前；第四相位L开始后，协调方向出口道交通流迅速上升至相交道路左转进口道饱和流量并持续至周期C结束.

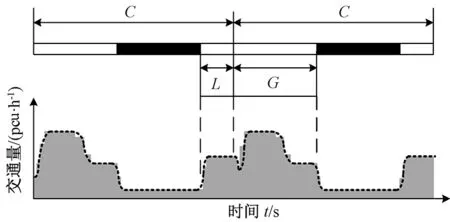
图1 “相交道路左转相位-协调方向相位”相序下干道出口道交通量变化特征Fig.1 Variation tendency for traffic of the arterial exit of the crossroad in circle when the phase for left turning of crossing road finished before the phase for the arterial started

当相交道路的左转相位L后置于协调相位G时，该相位为周期内的第二相位，周期内协调方向出口道交通量变化趋势如图2所示.周期开始后，协调方向交叉口出口道交通量从相交道路右转自由流迅速上升至协调方向饱和交通流，待协调方向进口道排队车辆清空后，出口道交通流逐渐转为自由流至相位G结束. 第二相位L执行时，协调方向出口道交通流由协调方向自由流转换为相交道路左转进口道饱和流直至第二相位结束.随后，由于协调方向出口道均只有相交道路右转车辆允许进入，协调方向出口道交通流将从相交道路左转进口道饱和流转为相交道路右转自由流直至周期结束.

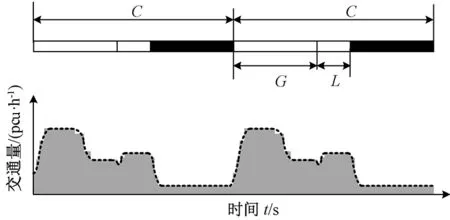
图2 “协调方向相位-相交道路左转相位”相序下干道出口道交通量变化特征Fig.2 Variation tendency for traffic of the arterial exit of the crossroad in circle when the phase for left turning of crossing road started behind the phase for the arterial

1.2 MULTIBAND基本模型

设Ii(i=1,2,…,n)为干线协调控制范围内的交叉口，协调方向MULTIBAND基本模型如式 (1～9)[2，12]所示.

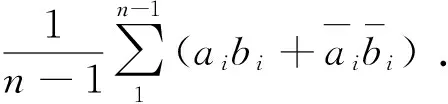
(1)

s.t

(2)

(3)

(4)

其中，i=1,2,…,n-1.

(5)

其中，i=1,2,…,n-1.

(6)

其中,i=1,2,…,n-1.

(7)

其中,i=1,2,…,n.

(8)

其中,i=1,2,…,n-2.

(9)

其中，i=1,2,…,n-2.

(10)

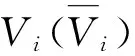
式 (2) 为模型的约束条件，可使协调方向上下行中交通量较大的一侧获得更大的带宽.式中，k为干线下行方向与上行方向的带宽需求比例.

式 (3) 为协调周期设定了上下限.式中，z为周期C的倒数；C1和C2分别为周期的下界和上界.

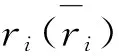
式组 (7) 则为排队清空时间率qi设置了最大值θ作为上限约束，以保证绿波的连续性.

1.3 基于相交道路左转交通量的模型改进分析

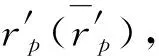
(11)

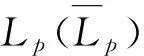
此时，考虑了相交道路左转饱和交通量的交叉口Ip处干线协调时距图如图3和图4所示. 其中图3为“相交道路左转相位-协调方向相位”相序，图4为“协调方向相位-相交道路左转相位”相序.

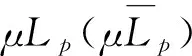
为配合基于相交道路左转流量的模型改进，还需以绿波带中心线为基准，对绿波带两侧带宽进行非对称化处理[13]. 记上(下)行方向绿波带中心线两侧的绿波带宽分别为bi′和bi″，

(12)

2 考虑相交道路左转饱和交通量的MULTIBAND改进模型

2.1 模型修改

为了非对称化处理绿波带两侧带宽，公式 (13)～(16)将用于替换基本模型中的公式 (1)、(2)、(4)、(5).

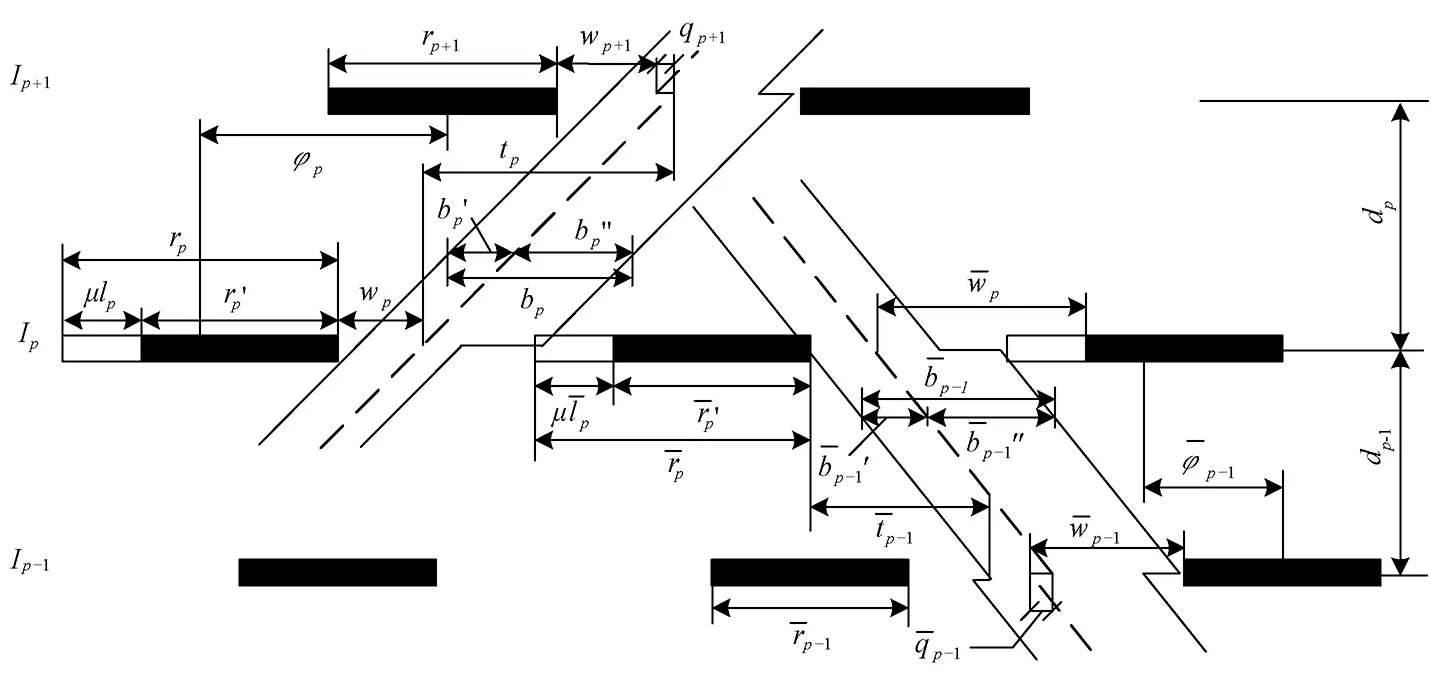
图3 “相交道路左转相位-协调方向相位”相序下交叉口p及其相邻交叉口绿波时距图Fig.3 Time-distance graph when the phase for left turning of crossing road finished before the phase for the arterial started

图4 “协调方向相位-相交道路左转相位”相序下交叉口p及其相邻交叉口绿波时距图Fig.4 Time-distance graph when the phase for left turning of crossing road started behind the phase for the arterial

(13)

(14)

其中，i=1,2,…,n-1.

(15)

其中，i=1,2,…,n-1.

(16)

其中，i=1,2,…,n-1.

2.2 模型扩充

与干线协调范围内的其它交叉口相比，交叉口Ip在模型计算中考虑了相交道路的左转饱和流量，所以在修改后的MULTIBAND基本模型基础上,增加公式组 (17)～(18) 描述相交道路左转相位前置于协调方向相位时各时间参数间的关系.

(17)

(18)

增加公式组 (19)～(20)，用于描述相交道路左转相位后置于协调方向相位时各时间参数之间的关系.

(19)

(20)

模型求解时，根据相交道路左转相位的相序位置选择公式组 (16)～(17) 或 (18)～(19) 加入修改后的MULTIBAND基本模型中联合求解. 当p=1时，只考虑相交道路左转流量对交叉口Ip上行方向交通量的影响，即取公式组 (16) 或 (18)；同理，当p=n时，仅考虑相交道路左转流量对交叉口Ip下行方向交通量的影响，即取公式组 (17) 或 (19).

3 案例分析

3.1 案例路段简介

长江路是镇江市重要主干道. 笔者选取长约1 500 m、双向四车道、包含五个交叉口的路段作为算例，各交叉口间的间距和相位长度如表1所示.

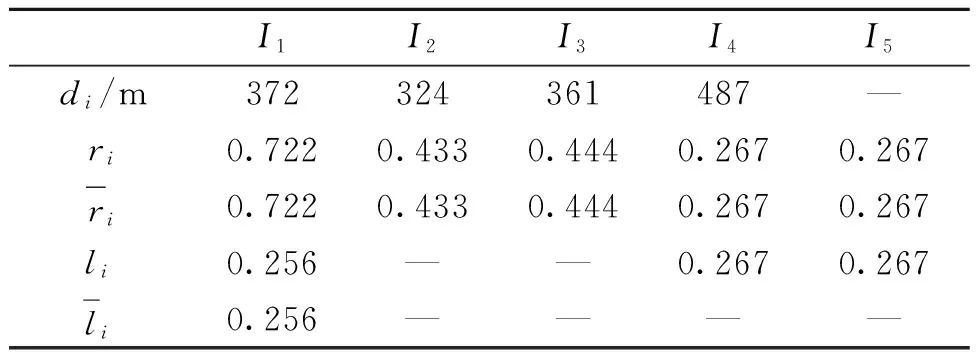
表1 干道协调控制范围内交叉口间的间距及相位时长Tab.1 Distance of crossroads and signal timing in arterial

交叉口I1为控制路段的关键交叉口，相交道路经左转汇入干道的交通量大，且干道直行红灯时间率长.因而建模时将该口相交道路左转流量纳入干线协调控制的考虑范围内. 设相交道路左转流量饱和度μ=0.6，附加因子ρ=1，带速以及带速变化量如表2所示.根据历史平均车速和限速进行标定. 所有参数标定后，通过LINGO软件对模型中的未知量进行求解.

表2 与速度有关的参数标定

3.2 结果分析

求解结果如表3和表4所示. 无论干道交通流处于何种状态，与基本模型相比，改进模型均可以获得更大的带宽，且较小的带宽标准差意味着各路段带宽更加均匀，有助于提高绿波的控制效果. 从改进模型的两种相序设置情况来看，相交道路左转相位后置于协调方向相位时，可获得的最大带宽更大，且带宽标准差更小，理论上的控制效果更优.

表3 各MULTIBAND模型求解结果统计(k=0.99)Tab. 3 Solution results for models of MULTIBAND (k=0.99)

3.3 模型仿真

模型的仿真由VISSIM软件实现，并在路段延误和交叉口停车次数两个评价指标上，与未考虑相交道路左转交通量的MULTIBAND基本模型进行比较，从而评价改进模型的控制效果. 为检验改进模型的协调控制能力，仿真中设置了两种干道交通流状态，即双向交通量趋同(k=0.99)状态和双向交通量不均衡(k=0.75)状态. 此外，改进模型在仿真时还将进一步划分为相交道路左转相位的早断和滞后两种情况，并对两种情况的控制效果进行评价.

表4 各MULTIBAND模型求解结果统计(k=0.75)Tab.4 Solution results for models of MULTIBAND(k=0.75)

将求解结果输入VISSIM中进行仿真，在双向交通量趋同和潮汐条件下，1 h的路段双向延误和平均停车等待时间统计分别如图5和图6所示.

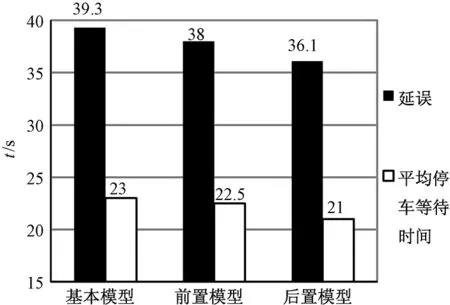
图5 各MULTIBAND模型双向仿真结果(k=0.99)Fig.5 Simulation results for models of MULTIBAND in two-way (k=0.99)

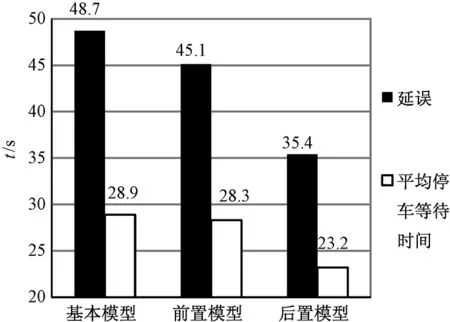
图6 各MULTIBAND模型双向仿真结果(k=0.75)Fig.6 Simulation results for models of MULTIBAND in two-way (k=0.75)

仿真结果也进一步证实了通过LINGO求解所得到的结论：在两种仿真环境下，MULTIBAND改进模型的控制效果均好于基础模型. 尤其是早断相序下的MULTIBAND改进模型在双向干道交通流处于潮汐流时，延误及平均停车次数相比基本模型分别降低了27.3% 和25.5%，控制效果比基础模型有较大提升. 进一步观察潮汐流下交通量较大一侧的仿真结果，如图7所示，更说明早断相序下的改进模型控制效果的优越性.

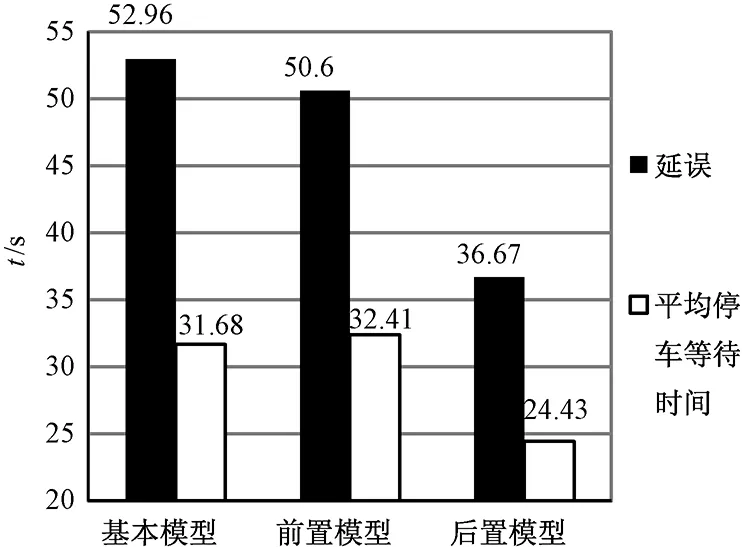
图7 各MULTIBAND模型上行方向仿真结果(k=0.75)Fig.7 Simulation results for models of MULTIBAND in up direction (k=0.75)

4 结论

笔者针对干线协调控制中关键交叉口相交道路的左转交通量在周期内易达到饱和的实际情况，将相交道路部分左转相位时间加入干道直行相位时间，使得相交道路的左转汇入交通量纳入干道协调控制范围，并据此对MULTIBAND基本模型进行修改和扩充. 求解和仿真结果说明，笔者所提出的MULTIBAND改进模型有效控制了干道交通量的总延误，具体来说，不仅降低了干道直行车辆在交叉口的排队次数和时间，也降低了转向汇入交通量对干道直行交通量通行的影响，提高了干道协调控制的效果，为干道双向绿波协调控制设计提供了一套实用性强、适用条件宽的新方案.

[1] MORGAN J T, LITTLE J D C. Synchronizing traffic signals for maximal bandwidth [J]. Operations research, 1964, 12(6):896-912.

[2] GARTNER N H, ASSMANN S F, LASAGA F, et al. Multiband: A variable bandwidth arterial progression scheme [J]. Transportation research record, 1990 (1287): 212-222.

[3] STAMATIADIS C, GARTNER N H. Multiband-96: A program for variable-bandwidth progression optimization of multiarterial traffic networks [J]. Transportation research record, 1996,1554(1): 9-17.

[4] 卢凯,郑淑鉴,徐建闽,等. 面向双向不同带宽需求的绿波协调控制优化模型[J]. 交通运输工程学报, 2011, 11(5): 101-108.

[5] 王世明,徐建闽,周沛,等. 基于左转早断与滞后相序的MAXBAND模型效益分析[J]. 公路交通科技, 2013(12): 259-262.

[6] 陈宁宁,何兆成,余志. 考虑动态红灯排队消散时间的改进MAXBAND模型[J]. 武汉理工大学学报(交通科学与工程版), 2009, 33(5): 843-847.

[7] 侯永芳.干线绿波交通信号控制方法研究[D]. 长春：吉林大学交通学院, 2015.

[8] 秦雅琴,熊坚,高晶,等. 驾驶模拟器动态交通流仿真与VISSIM系统数据接口研究[J]. 昆明理工大学学报(理工版),2007, 32(1): 77-79.

[9] 王炜,过秀成. 交通工程学[M]. 2版.南京:东南大学出版社, 2011.

[10] 沈家军,王群. 基于通行效率最优的交叉口控制方式优选[J]. 郑州大学学报(工学版), 2016, 37(3): 60-63.

[11] 王殿海. 交通流理论[M]. 北京: 人民交通出版社, 2002.

[12] DU R H. Urban traffic coordination control system based on multi-agent-game[J]. International conference on intelligent computation technology and automation, 2008,2:817-821.

[13] ZHANG C, XIE Y, SGARTNE Y N, et al. Am-band: an asymmetrical multi-band model for arterial traffic signal coordination[J]. Transportation research part C, 2015, 58:515-531.