基于最小二乘的四旋翼加速度计多源误差标定与补偿

北方工业大学电子信息工程学院 张 棋 冉 奇 张 旭

1.前言

加速度计是测量单位质量物体受到引力外的力即比力的仪表器件，目前已经成为航空航天[1]、智能交通[2]等多技术领域不可缺少的元件。在牛顿力学框架下，可以用于直接测量载体比力加速度，经过一、二次的积分后可以获取速度和位置信息。

制约加速度计精度的约束条件广泛存在，包括工艺、安装等诸多方面。目前基于集成工艺等硬件手段很难大幅度提高加计精度，或者成本较高。借助于软测量的技术手段，可以在低成本的约束下，实现对加速计精度的提升，已经成为获得高精度加速度计的重要技术方法[3]。

针对加速度计的标定，国内多许多学者开展了大量的方法和实验研究[4]。加速计的标定首先需要分析影响加速度计的主要因素，制约加速度精度的有安装误差、零偏、尺度因子、测量噪声等多源误差。其次需要建立含有多源误差的加速度计输出方程，进而借助于标定方法实现，高精度的标定。在加速度标定方法方面，目前有最小二乘方法[4]、总体最小二乘方法[5]和自标定[6]等方法。

为了便于分析和计算，定义如下坐标系[7]：

2.四旋翼的加速度计标定误差建模

加速度计的输出受到安装误差、尺度因子和零偏等多源误差影响，为获得高精度加速度计输出，需建立多源误差测量模型，进而将多源误差估计并补偿，该过程称为标定。首先研究加速度计静态输出下的比力方程，在载体相对于地球静止时，比力方程为[8]：

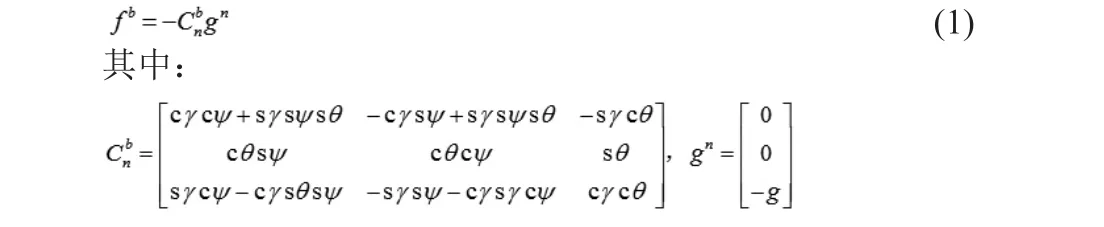
加计理想输出为：

本文将分别从安装误差、尺度因数、零偏和测量噪声等多类型误差分别分析并建模，给出较为实际的加速计输出模型。

(1)安装误差

加速度计是直接固定在载体上的，理论上三轴正交安装，安装坐标系和机体系轴线重合，但受安装误差的约束，两坐标系并不重合。

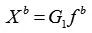
其中G为安装误差矩阵：

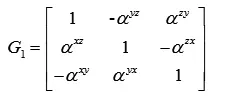
其安装误差角如图1所示。

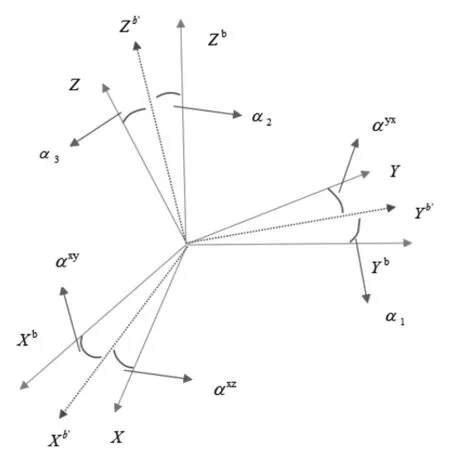
图1-安装误差角示意图

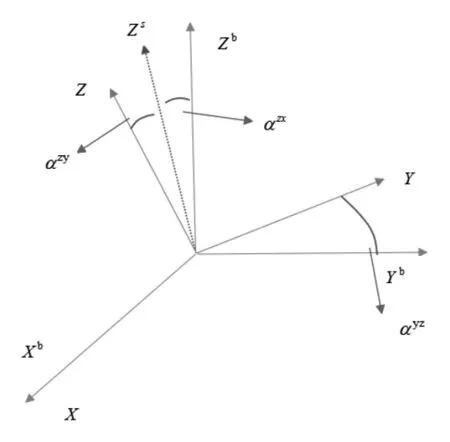
图2 简化的安装误差角示意图

此时方程(5)可以修正为：

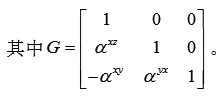
(2)尺度因子误差

尺度因子可以定义为加速度计传感器输出量和输入量的比值。定义分别表加速度计的x轴、y轴和z轴的实际使用中的刻度因子。

(3)零偏误差

零偏指无输入情况下的加速度计的平均输出，零偏和加速度计没有关系。

综合以上所得，（7）式为含多源干扰的加计量测方程。

3.最小二乘标定原理

通过取值平均的方法，可将测量噪声消除。在载体静态下获得真实的加速度，若矩阵和零偏b已知时，基于(7)式，可以得到其估计值为：

将(8)代入(3)得：

图3

4.实验仿真

实验使用微型四旋翼的加速度计数据获取的载体。从已有的数据中读取加速度计的x轴，y轴，z轴的测量结果，建立输入输出关系式，使用线性最小二乘实现未知参数的标定。

本次实验中采用低成本微型飞行器作为研究对象(如图3a图），我们通过上机位获取飞行器的三轴加速度计的数据（如图3b图）。

首先在实验中收集了两组组不同位置的加速度计单方向的数据，为了便于查看数据的变化，acc_X、acc_Y、acc_Z的变化曲线如图4所示。

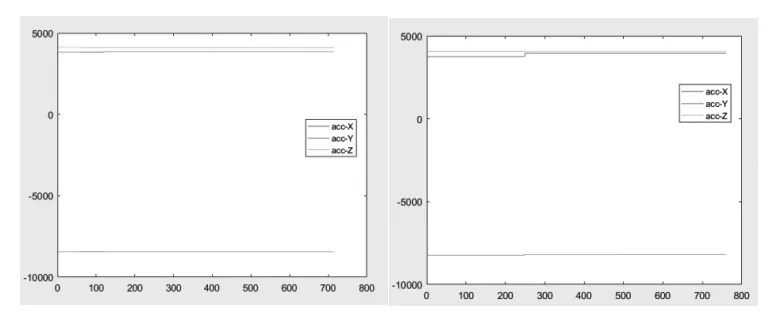
图4 两组加速度计的x、y、z轴获取数据的变化图，存在微小变化

通过MATLAB进行最小二乘标定绘图，可以的获取其位置信息，结果如图5所示。

图5 标定结果图

线性最小二乘标定加速度计的标定结算结果如下表所示：

5.结论

针对加速计实际输出值存在多源误差的问题，本文分析了影响加速度计精度的误差源问题，分析了安装误差，尺度因子，零偏和测量噪声，结合最小二乘方法的原理，分别研究了线性最小二乘和迭代最小二乘方法在实际加速计标定中的应用，仿真结果表明所提出方法的有效性。

[1]刘晓庆.捷联式惯导系统误差标定方法研究[D].哈尔滨工程大学,2008.

[2]王小春.MEMS加速度计误差的高精度标定方法[J].微纳电子技术,2012,11:743-749.

[3]陈稀军.加速度计高阶误差模型系数的标定方法[J].中国惯性技术学报,2010,18(4):508-512.

[4]黄苹.捷联惯导系统标定技术研究[D].哈尔滨工程大学,2005.

[5]袁豹,陆游.基于总体最小二乘的MEMS陀螺仪标定方法研究[J].勘察科学技术,2014(1):18-20.

[6]Frosio I,Pedersini F,Borghese N A.Autocalibration of MEMS accelerometers[J].IEEE Transactions on Instrumentation and Measurement,2009, 58(6):2034-2041.

[7]全伟,刘百奇,宫晓琳.惯性/天文/卫星组合导航技术[M].国防工业出版社,2011.

[8]秦永元.惯性导航[M].科学出版社,2006.