电子温度对527 nm强激光与等离子体作用的影响

夏雄平, 梁秋群, 高润梅, 王 柳

(桂林理工大学 理学院, 广西 桂林 541004)

在激光惯性约束核聚变(ICF)中, 强激光与物质相互作用会产生一种复杂的等离子体系统[1-3], 并产生大量电子等离子体, 其中热电子对ICF的影响使入射激光能量损失及靶核压缩率降低[4]. 在强激光与等离子体相互作用中, 产生大量非线性现象, 如自聚焦、 成丝及受激Raman散射等[5], 这些非线性现象对激光等离子体相互作用会产生重要影响. 如相对论效应使等离子体中的短脉冲强激光自聚焦趋势减缓, Raman散射可加速自聚焦的发展[6]; 在部分离化等离子体中, 激光自聚焦随电离程度的增大而增强[7]; 对于给定强度的激光脉冲, 随着等离子体密度的增大, 自相位调制会进一步增强激光脉冲的自聚焦[8]. Singh等[9]研究了碰撞性等离子体通道对激光束扭曲的影响, 结果表明, 激光束出现自聚焦和扭曲现象. 本文采用改进的傍轴模型和WKB近似, 考察等离子体中电子温度的变化规律及电子温度对等离子体性质和激光传播的影响. 所用脉冲激光为Gauss型, 波长527 nm, 脉冲宽度1～2 nm, 激光强度为6～8×1014W/cm2.

1 碰撞性欠稠密等离子体中电子温度及介电函数

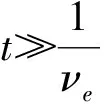
(1)

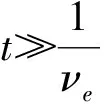
把Ve代入式(1)可得

(2)

波长527 nm强激光的光强为

其中A00为初始光强振幅. 在强激光与等离子体相互作用过程中, 若电子的碰撞频率远小于激光频率ω, 则电子温度可表示为初始等离子体温度T0与电子温度增量Ts之和, 即Te=T0+Ts. 此时电子温度与电子碰撞频率νe的关系为

(3)

将光强EE*、Te=T0+Ts和Ve代入式(2)可得

(4)

其中Tp0和Tp2分别表示沿径向的一阶和二阶电子温度. 将两个无量纲化参量代入式(4), 并采用分离变量法, 则电子温度增量与时间的变化关系方程可分解为两个电子温度分量的表达式：

(5)

(6)

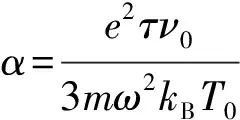
(7)

其中:ε0为线性部分;ε2为非线性部分, 由电子密度变化引起. 在相互作用过程中, 由于电子温度变化影响电子密度, 电子密度变化决定介电常数, 因此介电函数可转化为电子温度的变化关系：

(8)

其中:ωp0为电子等离子体的角频率;ω为激光的角频率. 将式(8)代入式(7)可得随电子温度变化的介电函数为

(9)

在强激光与等离子体相互作用中, 若忽略磁场的影响, 则其激光传播的波动方程为

2E-(

(10)

式(10)中光电场解的一般形式为

(r,z,t′)exp{i(ωt′-k0z)}.

(11)

=A00(r,z,t′)exp{-ik0S0(r,z,t′)}.

将式(11)代入式(10), 并利用分离变量法分离实部和虚部, 可得实部和虚部方程分别为

将式(11),(12)代入波动方程中, 利用方程两边带有系数r2的项相等, 从而得到反映激光束在等离子体中传播的光束宽度变化方程为

(14)

(15)

式(15)反映了激光在等离子体传播过程中光束宽度的变化, 其中右边第一项为发散项, 第二项为碰撞引起的非线性项, 可改变其介电函数及引起光束发生变化. 当第一项大时, 光束出现自散焦, 当两项平衡或第二项大时, 光束出现自聚焦.

2 数值模拟与讨论

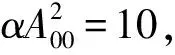
图2为介电函数(ε0,ε2)和时间的关系, 其中

曲线a,c,e和g分别对应δν0=0.5,1,2,3时的ε0； 曲线b,d,f和h分别对应δν0=0.5,1,2,3时的ε2. 由图2可见, 介电函数ε0和ε2呈振荡变化. 在有质驱动力和粒子间碰撞效应的影响下,ε0明显大于ε2,ε2出现两个峰值, 在线性部分仅有一个峰值, 且线性部分ε0在相同参数下明显高于非线性部分ε2, 该理论结果与文献[2]的实验结果相符. 随着碰撞效应的增强(δν0增加), 能量交换的速度加快, 导致粒子能量的损失加剧及电子温度发生变化, 从而引起介电函数降低, 即离子体中的介电函数变化明显依赖于电子温度.

图1 轴向电子温度(Tp0,Tp2)和时间的关系Fig.1 Relationship between axial electron temperature (Tp0,Tp2) and time

图2 介电函数(ε0,ε2)和时间的关系 Fig.2 Relationship between dielectric constant (ε0,ε2) and time

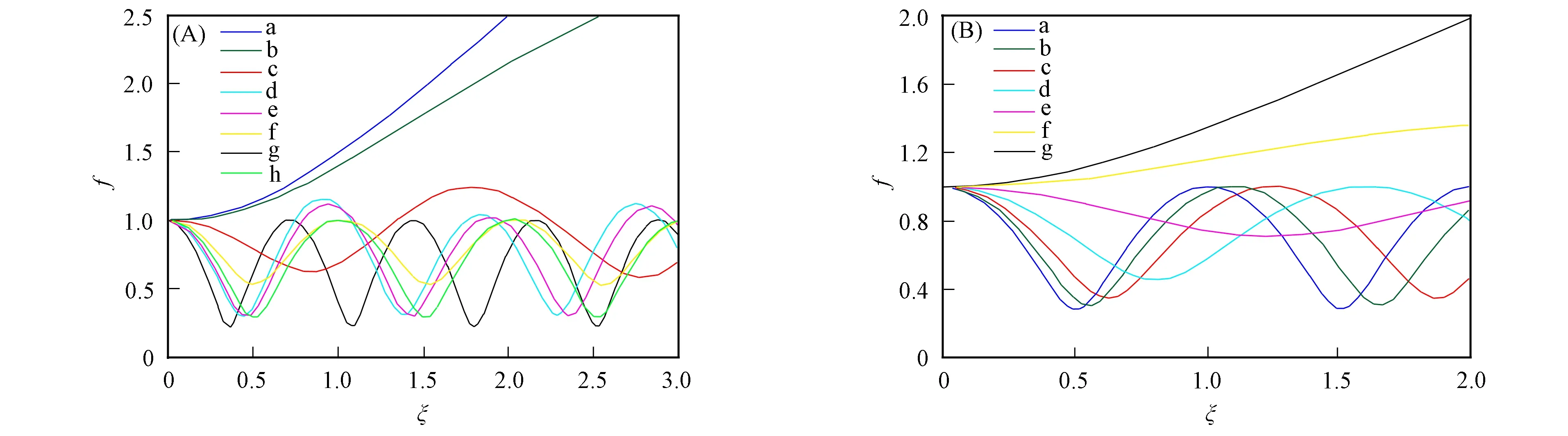
图3 激光束宽f与无量纲化传播距离ξ的关系Fig.3 Relationship between laser width f and dimensionless distance of propagation ξ

由图3可见, 束宽随传播距离的变化出现3种不同现象：

1) 束宽随距离的增加而不断增大, 如图3(A)中的曲线a和b及图3(B)中的曲线f和g；

2) 束宽随距离的增加而振荡增大, 如图3(A)中的曲线c和d；

3) 束宽随距离的增加呈余弦变化, 如图3(A)中的曲线e～g及图3(B)中的曲线a～e.

产生3种不同现象的原因是： 在等离子体中, 激光束宽方程中包含衍射影响下的分离项及非线性效应引起的收敛项, 当非线性效应不明显时, 衍射效应引起的光束分离起主导作用, 使得激光束宽随传播距离的增大而增大, 进而出现稳定分离； 随着非线性效应引起的光束收敛增强, 但尚未与衍射效应相当时, 束宽出现振荡分离； 当二者相等时, 出现自聚焦现象. 因此可通过激光束宽的变化检测等离子体对激光的吸收和转换效率, 由文献[6]可知, 束宽过大不利于对激光的吸收和转换, 通过改变激光束宽抑制非线性影响.

综上, 本文应用改进的傍轴理论和WKB近似, 通过求解电子能量的平衡方程与激光波动方程, 得到了在碰撞性欠稠密等离子体中电子温度的变化, 以及电子温度影响下的介电函数与激光束宽的变化. 数值模拟结果表明, 电子温度变化影响等离子体的介电函数和激光在等离子体中传播的性质. 在电子等离子体间的碰撞影响下, 电子温度呈振荡变化, 温度变化引起电子密度发生变化, 导致等离子体的介电函数也呈振荡变化. 介电函数的变化影响激光在等离子体中的传播性质, 使其束宽出现稳定分离、 振荡分离及稳定的自聚焦现象.

[1] Djebli M, Moslem W M. Self-similar Expansion of a Warm Dense Plasma [J]. Phys Plasmas, 2013, 20(7): 072702.

[2] 王传珂, 刘慎业. 527 nm激光间接驱动聚变潜在可能的实验研究 [J]. 激光与光电子学进展, 2008, 45(11)： 57-61. (WANG Chuanke, LIU Shenye. Experimental Study of Prospects for Indirect-Drive Inertial Confinement Fusion Driven by 527 nm Light [J]. Laser & Optoelectronics Progress, 2008, 45(11)： 57-61.)

[3] 李玉同, 廖国前, 赵刚, 等. 强激光高能量密度物理的若干进展和展望 [J]. 中国科学： 物理学 力学 天文学, 2013, 43(7)： 795-809. (LI Yutong, LIAO Guoqian, ZHAO Gang, et al. Progress and Prospects of High Energy Density Physics Driven by Intense Lasers [J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2013, 43(7)： 795-809.)

[4] Winkel M, Gibbon P. Spatially Resolved Electronic Correlations in Nanoclusters [J]. Contributions to Plasma Physics, 2013, 53(4/5): 254-262.

[5] 王形华, 郭旗, 谢逸群. 傍轴高斯光束在强非局域介质中的传输特性 [J] . 光学学报, 2005, 25(6)： 848-853. (WANG Xinghua, GUO Qi, XIE Yiqun. Propagation Properties of the Paraxial Gaussian Beam in Strongly Nonlocal Media [J]. Acta Optica Sinica, 2005, 25(6)： 848-853.)

[6] 闫喜亮, 郝东山. Compton散射对短脉冲强激光在次临界等离子体中自聚焦的影响 [J]. 光学技术, 2014, 40(1): 50-52. (YAN Xiliang, HAO Dongshan. Influences of Compton Scattering on the Self-focusing of the Intense Laser Pulse in Underdense Plasma [J]. Optical Technique, 2014, 40(1): 50-52.)

[7] 刘明萍, 柳剑鹏, 罗荣祥, 等. 强激光脉冲在部分离化等离子体中的传播特性 [J]. 强激光与粒子束, 2014, 26(7): 072006. (LIU Mingping, LIU Jianpeng, LUO Rongxiang, et al. Propagation Properties of an Intense Laser Pulse in Partially Stripped Plasma [J]. High Power Laser and Particle Beams, 2014, 26(7): 072006.)

[8] 柳剑鹏, 陶志鹏, 陶向阳. 强激光脉冲在部分离化等离子体中的自聚焦 [J]. 江西师范大学学报(自然科学版), 2014, 38(5): 464-467. (LIU Jianpeng, TAO Zhipeng, TAO Xiangyang. The Self-focusing of a Short Laser Pulses in Paratially Stripped Plasma [J]. Journal of Jiangxi Normal University (Natural Science), 2014, 38(5): 464-467.)

[9] Singh N, Singh A. The Effect of Plasma Channel on the Self-distortion of Laser Pulse Propagating through the Collisionless Plasma Channel [J]. Journal of Nonlinear Optical Physics & Materials, 2014, 23(3): 1450027.