融合Morlet小波与GA优化多模态核的轴承故障检测算法

杨 琦

(安徽工业大学 工程实践与创新教育中心, 安徽 马鞍山 243002)

在旋转机械故障中, 35%以上的故障由轴承故障引起, 所以对轴承故障的自动检测已成为本领域的研究热点[1-3]. 作为动态系统的轴承故障检测, 其早期故障信号变化较微弱, 为了能更好地检测出微弱故障, 提取区别性较强的微弱故障特征是故障检测的关键, 良好的特征不但能提高故障检测的准确度, 而且能提升检测效率[4]. 实际上, 机械设备故障的结构形式多样, 激励荷载种类较多, 频谱分布也较广, 以及多种边界条件等其他限制因素, 所以稳定的故障特征提取难度较大[5]. 采用传统的频带能量特征、 Fourier变换特征以及能量谱特征等方法[6], 面对微弱变化特征的鲁棒性较差, 对于故障检测的分辨率较低. 为了使提取到的特征有更强的分辨性[7], 本文采用Morlet小波变换提取特征.

目前, 通过信号特征进行轴承故障分类检测的方法较多, 一般采用机器学习的方法[8], 常用的机器学习模型包括K近邻、 人工神经网络、 线性判别分析、 随机森林以及支持向量机(SVM)[9-10]等. 而在轴承故障检测过程中, 通常产生的故障信号样本量较小, 属于小样本机器学习范畴, 采用SVM进行数据分析的效果较好, 能保证特征数据集的欠拟合与过拟合问题. 但传统SVM采用单一核方法完成特征映射与分类, 对于微弱特征的映射效果较差, 所以本文采用多模态融合核方法, 并采用遗传算法(GA)对多模态融合参数进行优化, 以获得对小样本轴承故障检测最优化的分类检测模型.

1 Morlet小波变换特征

小波变换与Fourier变换不同, 拥有多种谐波族可供选择, 利用不同的小波基函数可获得完全不同的小波变换特征, 在众多小波基函数中, Morlet基函数小波族对动态系统的模拟有较强的鲁棒性, 主要有以下两种原因：

1) Morlet小波的幅值是按指数衰减的谐波信号, 而在动态系统中, 指数衰减的响应很常见, 所以Morlet小波能很好地模拟动态系统；

2) Morlet小波族中的各小波分别有自己的单值频率, 若分析的动态系统信号中有与某个单值频率相匹配的频率, 则相应的小波频率就能表征出该动态系统中的某些固定频率.

根据Morlet小波变换的特征, 本文通过先构建Morlet小波变化模型, 用于提取故障检测时的微弱故障特征, 再通过融合核方法构建出SVM分类器, 最后采用遗传算法优化SVM参数, 提升对故障检测的效果和效率.

假设动态系统信号x(t)的能量值表示为x(t)∈L2(R), 则可将连续小波变换通过原始动态系统信号与小波族之间的内积表示. 小波族是由各种子小波ga,b(t)组成的集合, 子小波拥有多个形态, 由母小波g(t)通过伸缩和平移共同变换所得, 变换关系为ga,b(t)=g((t-b)/a), 其中:a表示伸缩变换的尺度参数;b表示平移变换的位移参数. 由多个子小波共同构成的小波变换为

(1)

1) 保证母小波g(t)的定义域是紧密的, 保证函数拥有单调性, 从而可产生对时间的局部化差异；

2) 满足母小波g(t)的容许条件

(2)

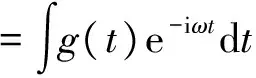
实际应用中, 像轴承这类动态系统中经常会出现冲击衰减类波形, 而Morlet也呈现该冲击衰减特性, 所以在进行轴承故障检测时, 采用Morlet小波将会与轴承信号形成特征配对. Morlet小波由最小时频窗面积的高斯函数构成, 能表达出局部的视频特性, Morlet小波定义为

(3)

其中,fb和fc分别表示形状参数和中心频率, 用于表示震荡衰减的快慢程度和震荡频率. Morlet小波在进行变换时复数部分在频域滤波上通常会产生相位失真, 所以在提取Morlet小波变换特征时只考虑其实数部分, 作为小波变换的母小波：

(4)

该实数部分的母小波Fourier变换可表示为

Gr(af)=exp{-π2fb(af-fc)2}.

(5)

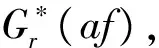
(6)

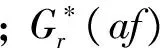
2 支持向量机与多模态融合核方法

2.1 支持向量机

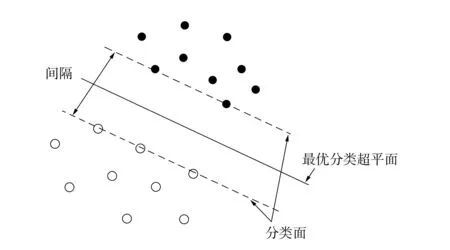
图1 故障检测的最优分类面Fig.1 Optimal classification surfaces of fault detection

支持向量机是一种通过求解线性分类面将特征分离的方法. 假设经过Morlet小波变换后产生的特征集为{xi,yi,i=1,2,…,n}, 在该特征集合中,x表示需要分类的特征集合,y表示分类结果标签, 即是否发生故障或发生故障的类型, SVM分类器需要寻找一个最优的分类面w*x+b=0, 使得特征集合能尽可能大的分离开, 从而能通过该“最优化分类面”完成故障的检测或故障类型的检测. 图1为故障检测的分类面示意图, 其中黑色圆点部分表示无故障信号提取到的Morlet小波特征, 而白色圆点部分表示有故障信号提取到的Morlet小波特征, 通过“最优分类面”可较好地完成二者之间的分类.

在分类面的表达式中,w表示分类面的权重(二维空间上表示斜率),x表示支持向量, 满足最多支持向量分类正确的分类面为最优分类面,b表示加性偏置. 为了获得最优化的分类面, 就要求最优化条件下的w,b, 实际上是一个二次规划问题[11]：

为了求解上述带限制条件的二次规划问题, 通常采用Largrange乘子法和KKT(Karush-Kuhn-Tucker)条件求解, 以获得最优分类结果下的w和b, 使故障检测结果最佳.

在动态系统的故障检测中, 不是所有信号都能获得线性可分的特征, 线性不可分的数据很难只通过一个线性分类面将其区分, 因此, SVM加入松弛变量允许少量样本被错分, 从而在最大分类结果和最小错分结果两个限制条件下完成SVM的分类问题. 实际应用中, 多数动态系统的故障都是由微弱特征产生的, 有较大的非线性过程, 通常采用松弛变量也不能较好地解决特征的错分问题. 此时采用核函数, 将原来线性不可分的数据通过核函数进行变换, 在新的变换空间下成为线性可分的数据, 再通过松弛变量, 即可较好地解决动态系统故障的微弱特征分类问题. 图2为核函数的应用实例, 通过将原来线性不可分的数据变换到高维空间上, 使其线性可分性更好.

图2 非线性特征通过核函数变化为高维线性可分特征Fig.2 Nonlinear characteristics are transformed into high dimensional linear separable characteristics through kernel function

引入核函数后, SVM的二次规划问题转化为

其中:φ(x)表示核函数;ξi表示松弛因子;C表示惩罚系数. 通过Largrange乘子法求解最优化问题, 并使用KKT条件求解优化问题, 得出核函数条件下非线性SVM分类面为

(12)

其中K(xi,xj)表示核函数, 通过核函数的变换可使故障检测过程中的微弱特征变得更清晰, 使分类结果更精确.

2.2 融合多模态核方法

目前, 核函数的选择主要采用全局尝试, 通过尝试所有核函数, 从中选择最优结果作为数据分类使用的核函数. 常见的核函数包括以下4种[12]：

上述几种核函数中, 既有局部性强的线性核函数, 也有全局性强的径向基核函数. 在轴承故障检测中, 既需要信号的全局信息特征, 又需要信号的局部信息特征, 所以本文提出一种多模态融合核函数选择规则, 在该规则下采用权重α,β融合全局核函数以及局部核函数, 即通过下式计算出多模态融合核函数：

Kmix=αKLINE+βKRBF,

(13)

其中:KLINE表示线性核函数, 是局部核函数;KRBF表示径向基核函数， 是全局核函数; 权重α,β用于计算二者之间的融合权重.

[13], 所有权重都通过实验结果获得, 通过选择不同的融合权重以获得最优化的结果. 该方法一般会陷入局部极小值, 难以获得全局最优的权重, 实际上也会带来大量的时间消耗, 不利于最优权重的选择. 为了优化本文多模态融合核函数的权重值, 使其能最优化的分配出线性核函数和径向基核函数之间的关系, 采用遗传算法对其进行优化, 使融合函数能最大限度地完成轴承故障检测.

2.3 遗传算法解决融合核函数权重

遗传算法能很好地解决参数优化问题, 避免陷入局部极小值. 本文分别对原始种群进行选择、 交叉和基因突变操作, 从而在搜索空间搜索出全局最优解和局部最优解, 并保证样本的多样性, 同时也具有较强的搜索效率和全局寻优能力[14].

采用遗传算法优化多模态核函数参数α,β的步骤如下.

1) 基因编码. 基因编码是遗传算法的前提条件, 遗传算法的交叉和变异都建立在基因编码上, 采用遗传算法自适应优化多模态融合核函数参数α,β, 可以充分发挥SVM的性能, 本文对遗传算法种群的编码方法为

X=(x1,x2)T,x1∈[-5,5],x2∈[-5,5].

(14)

2) 选择操作. 遗传算法的过程为选择更优秀的基因, 即适应度更高的数据, 在实际应用中, 可以采用精英策略, 选择其中一小部分适应度较高的优秀基因不参与选择和交叉等遗传操作, 直接进入下一代迭代, 该策略既能有效保证算法的收敛性, 又能减少数据处理量, 提升遗传算法的效率.

3) 交叉操作. 采用交叉操作能表现出群体的多样性, 增大遗传算法的搜索空间, 本文采用的交叉算子为自适应算子：

(15)

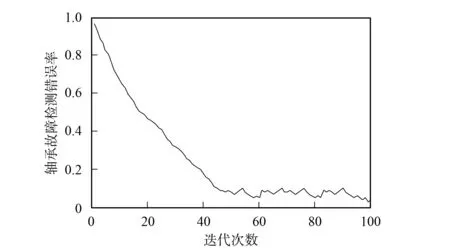
其中:fc表示交叉操作两个个体中适应度较大的个体;fmax和favg分别表示当前群组中的最大适应度值和平均适应度值; 通过0

4) 基因突变操作. 基因突变模拟人类遗传过程中发生的基因突变, 可增强群组的局部搜索能力, 突然改变某些个体的适应度值, 可有效增强个体的多样性, 降低陷入局部极小值的风险, 本文采用下列方法完成基因突变操作：

(16)

5) 损失函数和迭代次数. 损失函数是衡量当前遗传代数优化程度的指标, 为了获得最优化的多模态融合核函数参数α,β, 可以定义由当前α,β形成的多模态SVM对测试样本识别的错误率作为损失函数, 优化的目标是通过不断的选择、 交叉、 基因突变获得最小的错误率. 基于SVM测试识别错误率的损失函数定义为

(17)

其中:T表示需要被分类的总故障数;t表示被正确分类的故障数. 通过该损失函数可找出最优化目标. 最大遗传代数设为m=100.

因此, 在实际轴承故障检测中, 首先对每种故障信号分别提取Morlet小波变换特征, 然后分别构建多模态融合核函数SVM, 并用遗传算法优化多模态融合核函数的权重参数, 最后获得最优参数构建出SVM分类器, 对轴承故障信号进行诊断测试, 算法流程如图3所示.

图3 融合Morlet小波和GA优化多模态核函数的轴承故障检测算法流程Fig.3 Flow chart of bearing faults detection algorithm based on Morlet wavelet and multi-mode kernel optimized by GA

3 故障检测实验与结果分析

为了进一步验证本文提出算法的有效性, 下面针对实际轴承信号数据进行轴承故障检测. 轴承故障数据选择UoCn的智能维护中心数据集[15], 该数据集在实验中将4个轴承通过滚珠安装在同一轴承上, 轴承的转速设为2 000 r/min, 对轴承施加的径向载荷力为26 671 N, 轴承的水平方向和竖直方向分别安装了敏感度强的加速度传感器, 用于检测两个方向的加速度, 轴承信号的采样率设置为20 kHz, 共进行3组实验, 信号的采样间隔为10 min, 每个间隔共采集到20 480个数据点, 该数据集共持续164 h. 实验故障采集主要包括滚珠故障、 内圈裂纹故障和外圈裂纹故障3种类型, 为了检测出轴承信号中的故障, 并进行轴承诊断, 本文从总体带故障的数据中提取出60组, 每组提取1 024个数据点进行分析, 将其中的50组数据作为训练数据, 余下10组数据作为测试数据. 实验过程首先提取所有60组数据的Morlet小波变换特征, 然后构建多模态融合核函数, 并使用遗传算法对融合参数进行优化, 采用留一交叉验证法进行测试, 将留一交叉验证结果的均值作为损失函数.

图4 遗传算法对每种故障检测融合 核函数的迭代优化结果Fig.4 Iterative optimization results of GA for each fault detection fusion kernel function

提取完Morlet小波变换特征后, 建立多模态融合核函数并采用遗传算法优化融合参数α,β. 图4为采用遗传算法对多模态融合核函数参数优化的遗传代数与留一交叉验证均值之间的关系结果. 由图4可见, 在迭代初期, 遗传算法能快速降低故障检测的误差率, 当遗传代数超过50次时, 误差的降低逐渐趋于平稳, 误差的变化为单调递减的趋势. 图5为某组外圈故障训练样本的原始信号及其小波变换特征, 图5(B)～(E)分别给出了Morlet小波变换特征的实数部分、 虚数部分、 平方包络及其频谱示意图, 其中,fm表示频率的峰值部分.

表1列出了滚珠故障、 外圈裂纹故障、 内圈裂纹故障的多模态融合核函数参数优化结果及其相应的最小错误率以及迭代时间消耗. 由表1可见, 多模态融合核函数对于3种故障的检测错误率均较小, 通过遗传算法对多模态融合核函数参数的优化, 可完成对轴承故障的检测. 此外, 本文还针对单核函数与多模态融合核函数之间的性能进行了对比实验, 并以随机森林的结果作为基准进行对比. 表2和表3分别列出了对比实验错误率及时间效率的结果. 由表2和表3可见, 采用多模态融合核函数虽然需要更多的时间消耗来优化融合参数, 但能在一定程度上提升轴承故障的检测正确率.

图5 某原始故障信号与Morlet小波变换特征提取结果Fig.5 Feature extraction results of original fault signal and Morlet wavelet transform

故障类型 多模态融合核函数参数结果αβ检测错误率/%检测时间/ms滚珠故障0．84260．58631．262837内圈裂纹故障0．45860．64810．972938外圈裂纹故障0．69850．369871．162747

表2 3种核函数及随机森林的检测错误率(%)比较

表3 3种核函数及随机森林的检测效率(ms)比较

综上所述, 为了更好地解决轴承故障检测问题, 确定最佳维修时机, 并提升设备利用率及使用安全性, 本文提出了一种融合Morlet小波变换特征和GA优化的多模态核方法的轴承故障检测算法. 该算法能提取鲁棒性良好的Morlet小波变换特征, 然后将其输入到多模态核方法的分类模型中进行训练, 采用遗传算法优化多模态融合核函数参数, 将留一交叉验证错误均值作为损失函数, 最终优化得到合适的融合核函数参数建立分类检测模型, 完成轴承故障的检测, 利用少量的时间代价换取了检测准确率的提升.

参考文献

[1] 代宏伟. 引入权重分析优化的铁路动车轴承故障检测 [J]. 科技通报, 2014(6): 43-45. (DAI Hongwei. The Fault Detection of Railway Moving Bearing with Weight Analysis Optimization Is Introduced [J]. Report of Science and Technology, 2014(6): 43-45.)

[2] 李军利, 李巍华. 一种半监督SVDD-KFCM算法及其在轴承故障检测中的应用 [J]. 计算机科学, 2015, 42(z1): 134-137. (LI Junli, LI Weihua. A Semi-supervised SVDD-KFCM Algorithm and Its Application in Bearing Fault Detection [J]. Journal of Computer Science, 2015, 42(z1): 134-137.)

[3] 张新鹏, 胡茑庆, 程哲, 等. 信号稀疏分解理论在轴承故障检测中的应用 [J]. 国防科技大学学报, 2016, 38(3): 141-147. (ZHANG Xinpeng, HU Yiqing, CHENG Zhe, et al. The Application of Signal Sparse Decomposition Theory in Bearing Fault Detection [J]. Journal of National Defense Technology University, 2016, 38(3): 141-147.)

[4] LIU Haiyang, HUANG Weiguo, WANG Shibin, et al. Adaptive Spectral Kurtosis Filtering Based on Morlet Wavelet and Its Application for Signal Transients Detection [J]. Signal Processing, 2014, 96: 118-124.

[5] 廖辉, 邓四二, 王春艳, 等. 小波分析技术在矿山机械轴承故障检测中的综合应用 [J]. 矿山机械, 2014, 42(6): 122-126. (LIAO Hui, DENG Si’er, WANG Chunyan, et al. The Application of Wavelet Analysis Technique in Fault Detection of Mechanical Bearings in Mines [J]. Mining Machinery, 2014, 42(6): 122-126.)

[6] Czajkowski K M, Anna P, Rafal K. Single-Pixel Imaging with Morlet Wavelet Correlated Random Patterns [J/OL]. 2017-09-22. http://arxiv.or/abs/1709.07739.

[7] Neto O P, Pinheiro A O, Pereira V L, et al. Morlet Wavelet Transforms of Heart Rate Variability for Autonomic Nervous System Activity [J]. Applied and Computational Harmonic Analysis, 2016, 40(1): 200-206.

[8] 朱韶平. 基于LDA模型的滚动轴承故障类型检测 [J]. 轴承, 2014(7): 42-46. (ZHU Shaoping. Detection of Rolling Bearing Fault Type Based on LDA Model [J]. Bearings, 2014(7): 42-46.)

[9] Gryllias K C, Ioannis A A. Estimation of the Instantaneous Rotation Speed Using Complex Shifted Morlet Wavelets [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 78-95.

[10] 马伦, 康建设, 孟妍, 等. 基于Morlet小波变换的滚动轴承早期故障特征提取研究 [J]. 仪器仪表学报, 2013, 34(4): 920-926. (MA Lun, KANG Jianshe, MENG Yan, et al. Study on Early Fault Feature Extraction of Rolling Bearing Based on Morlet Wavelet Transform [J]. Chinese Journal of Scientific Instrument, 2013, 34(4): 920-926.)

[11] 杨望灿, 张培林, 张云强, 等. 基于邻域自适应局部保持投影的轴承故障诊断模型 [J]. 振动与冲击, 2014(1): 39-44. (YANG Wangcan, ZHANG Peilin, ZHANG Yunqiang, et al. The Bearing Fault Diagnosis Model Based on Neighborhood Self-adaptation Is Maintained [J]. Vibration and Shock, 2014(1): 39-44.)

[12] LIN Jing, QU Liangsheng. Feature Extraction Based on Morlet Wavelet and Its Application for Mechanical Fault Diagnosis [J]. Journal of Sound and Vibration, 2000, 234(1): 135-148.

[13] ZHENG Haibao, Li Z, Chen X. Gear Fault Diagnosis Based on Continuous Wavelet Transform [J]. Mechanical Systems and Signal Processing, 2002, 16(2/3): 447-457.

[14] 颜晓娟, 龚仁喜, 张千锋, 等. 优化遗传算法寻优的SVM在短期风速预测中的应用 [J]. 电力系统保护与控制, 2016, 44(9): 38-42. (YAN Xiaojuan, GONG Renxi, ZHANG Qianfeng, et al. The Application of Optimized Genetic Algorithm for Optimization of SVM in Short-Term Wind Speed Prediction [J]. Power System Protection and Control, 2016, 44(9): 38-42.)

[15] Zhou E, Fu M C, Marcus S I. A Particle Filtering Framework for Randomized Optimization Algorithms [C]//Winter Simulation Conference. Piscataway, NJ: IEEE, 2008: 647-654.