谈数学核心素养背景下的教学设计

摘 要:在强调素质教育的今天,人们常提出要关注对学生数学素养的培养。但受应试教育的影响,在很多实际的课堂教学中仍以教师讲授和学生练习为主,对关注数学素养的问题仍停留在理论层面不能真正落实。那数学素养包括哪些方面,我们又如何在日常教学中渗透对学生数学素养的培养呢?本文将从《定积分的概念》一节的教学设计出发进行研究。
关键词:稚化思维;最近发展区;积分思想;数学文化;数学情感
在强调素质教育的今天,人们常提出要关注对学生数学素养的培养。但受应试教育的影响,在很多实际的课堂教学中仍以教師讲授和学生练习为主,对关注数学素养的问题仍停留在理论层面不能真正落实。那数学素养包括哪些方面,我们又如何在日常教学中渗透对学生数学素养的培养呢?本文将从《定积分的概念》一节的教学设计出发进行研究。
一、
稚化思维,从同学们的最近发展区设置问题情境
定积分问题毕竟是大学的内容,对于很多高中的同学来说确实有一定难度。因此上课前一定要站在学生的角度,从学生的最近发展区出发设置问题情境,放低教学的起点、尽量用生动活泼的语言和情境激发学生的学习兴趣和探究欲望。于是我在广泛查阅资料后决定在本节课开始时先请同学们欣赏熟悉的长江三峡的美景(幻灯片展示),在广阔的江面上横跨着长江三峡大坝,将长江一分为二。上游的高峡平湖和下游的滔滔江水形成了鲜明的对比。在夕阳的余晖里,这里经常出现“一道残阳铺水中,半江瑟瑟半江红”的美景!这样诗情画意的情境使课堂轻松愉快,自然地将课堂气氛调动起来。然后提出问题:要建造这样的大坝,当然是要尽可能准确地计算它的截面面积。大坝的截面图是这样的:最上面AB段是一段抛物线,中间BC段是直线段,下面一段是圆弧(幻灯片展示图1)。请同学们讨论计算截面积的方法。同学们积极讨论、大胆尝试各种做法。因为学生从小学就熟悉割补法,有很多同学想到将截面切割成几个部分去计算。学生完全进入课堂的“角色”积极思考,然而还是有个问题难以解决:中间梯形的面积容易计算,但左边曲边梯形和右边曲边三角形的面积又该如何计算呢?于是,同学们带着疑问和浓浓的求知欲进入今天的新课。
二、 回归本源,从同学们熟悉的问题入手展示积分的思想
接下来就开始讲曲边梯形面积的求法吗?当然不是。要想让同学们对定积分的概念理解透彻,在这里就切入主题还是铺垫不够的。于是我首先肯定了同学们提出的“分割的思想”,并指出这种思想方法在小学课堂中就有所体现。回顾“曹冲称象”的故事。大象是一个整体,不容易称体重。曹冲很聪明,利用载相同质量的物体时船的吃水深度不变,将大象的体重等价转化成了一堆小石子的重量之和。然后称量所有小石子的重量,加起来就是大象的体重。这其中就先“化整为零”分割,再“积零为整”的求和,将不易解决的问题巧妙地解决了,体现了化归与转化的思想方法。
三、合作探究,突出学生的主体作用
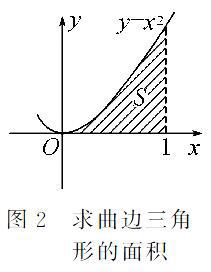
形的面积接下来,在以上设置情境和铺垫的引导下,学生心中对如何求曲边梯形的面积问题已经有了基本的想法,下面应该以动手实践、自主探究、合作交流为学习的重要形式。这时教师就要设置问题,给学生创造一个个思维的台阶,引导着学生一步步探索,让学生探索的难度与深度层层递进。因此,教师可以设计一个表格,让学生类比刚才的例子,先找到解决问题的大概思路。然后在具体操作上,为了便于研究,不妨把问题简化,先请同学们分组讨论研究x=1、y=0和曲线y=x2所围成的曲边三角形的面积S(幻灯片展示图2)。
仍不用具体计算,先请学生讨论有哪些可行的方法和步骤。这样设计就更加贴近学生的最近发展区,降低了问题探究难度,大大增加了同学们成功的体验。这样每个小组应该都能提出自己的思路,于是经过小组讨论、合作探究后,可以请小组进行展示。
接下来我引导学生分组分工合作,具体算一算区间五等分时求得面积的过剩近似值、不足近似值分别是多少,并请几位同学板书求解过程。经过这样的探究和动手验算,学生就可以轻松愉快的掌握求曲边三角形面积近似值的方法。
四、数学文化,激励科学精神、培育数学情感
科学家的科学精神和科研历程是一笔无形的财富,激励着一代又一代的学子奋发向上。尤其定积分思想作为数学思想的精华,它的发生和发展的历程更应该作为数学教育的题材介绍给学生。定积分的思想在我国古代魏晋时期的数学家刘徽的割圆术中就有体现:“割之弥细,所失弥少。割之又割,以至于不可割,则与圆合体而无所失矣。”还有古希腊数学家阿基米德也是利用定积分的无限分割的思想来推导球的体积和表面积。用幻灯片略作展示,这些灿烂的数学文化和巧妙的思维方式再次激起学生的极大的兴趣和热情,让学生充满对数学的欣赏和赞叹。同时激发了学生的民族自豪感和爱国主义情怀。
苏格拉底曾经说过:“教育不是灌输,而是点燃智慧。”如何上好一节数学课,我想精髓就在这里。如果再能用诗化的语言揭示数学的神奇与美妙,创设数学的文化意境,使学生产生丰富的联想和创造灵感就更好了。总之,关注学生的数学素养在于思想、在于意识、在于行动。
参考文献:
[1]普通高中数学课程标准(试验).人民教育出版社,2003(4).
[2]九章算术.
作者简介:
郭颍南,安徽省阜阳市,安徽省阜阳市第五中学。

