立式轴流泵装置压力脉动特性的试验

赵浩儒，杨 帆，吴俊欣，陈世杰，武 蒙

（1.扬州大学，江苏扬州 225009；2.江苏省水利勘测设计研究院有限公司，江苏扬州 225127）

1 前言

引起泵装置内部压力脉动的原因较多，如汽蚀、进口流速不均、过流部件中流场的速度和压力分布不均匀及机组过渡过程产生的压力和速度变化等。压力脉动峰峰值若超过允许范围将会导致水泵产生振动和噪声，甚至导致叶片产生裂纹，降低水泵效率，直接影响泵装置的安全稳定可靠运行，因此对泵装置压力脉动的研究显得非常重要［1］。目前，国内外学者对泵装置内部脉动的研究主要集中于：采用CFD软件对叶片泵及泵装置内部压力脉动进行数值模拟研究［2～5］；采用物理模型试验对泵装置内部压力脉动进行研究［6～10］；流态对叶片泵内部压力脉动的影响规律［11～13］。

因轴流泵装置压力脉动试验测试装置所需成本较高，当前主要采用数值模拟的方法，但数值模拟只能对测试结果进行间接性的预测，不能精准地反映实际情况，存在一定的误差。为了获得准确的试验结果，本文在分析前人研究成果的基础上，通过构建水力机械闭式试验台，搭配相应的脉动测试仪器和软件，对不同流量时立式轴流泵装置进行压力脉动测试，旨在获得准确的压力脉动信号数据。

2 试验装置及试验测点布置

水力机械闭式试验台如图1所示，包括模型泵测试装置；LDG-125S-92型0.5级电磁流量计1台；ISWH125-100A型304不锈钢材质管道离心泵1台；JCO型0.1级扭矩传感器1台，JW-3扭矩仪1台；EJA110A型0～100 kPa压差变送器1台；高频动态传感器，信号采集仪及配套分析系统，并配备相应的电动机，闸阀，管道等。其中叶轮的叶片数为4，导叶体叶片数为5，试验运行额定转速为2200 r/min，各项参数如表1所示。

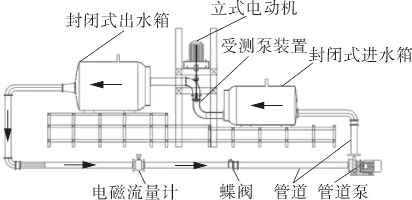
图1 试验装置示意

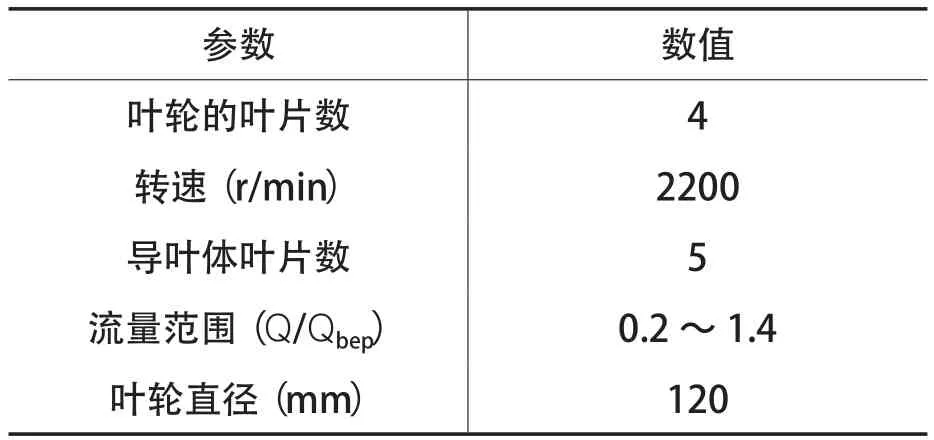
表1 主要参数

试验中采用压差变送器测量泵装置的扬程，电磁流量计测试流量，通过二次仪表的信号转换直接采集扭矩、转速、扬程和流量信号数据。试验方法依据SL140-2006《水泵模型及装置模型验收试验规程》，压力脉动测点选择了进水流道出口段A-A处壁面的P1、P2、P3，每个监测点间隔120°。出水流道渐扩段B-B处壁面上设置P4、P5、P6、P7，每个监测点间隔90°。共设置7个监测点，因篇幅限制只对监测点P1，P2，P4，P6进行分析，压力脉动监测点布置如图2所示。

图2 压力脉动监测点布置

3 试验结果及分析

3.1 能量性能试验

通过能量性能试验得到立式轴流泵装置流量、扬程及效率之间的关系，如图3所示。试验所测立式轴流泵装置最高效率为74.37%，此时的叶片安放角为0°，流量为31.04L/s，扬程为1.60m。为得到不同流量工况时各监测点压力脉动的变化规律，分别取0.3Qbep，Qbep，1.2Qbep共 3 个流量工况对上述7个压力脉动监测点的脉动幅值进行分析。

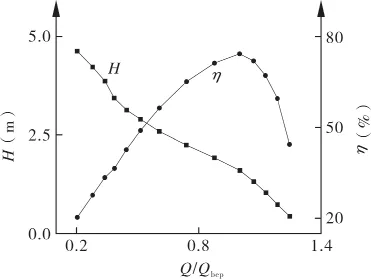
图3 模型泵装置性能曲线

3.2 压力脉动时域分析

选取P1，P2，P4，P6压力脉动监测点，分别在0.3Qbep，Qbep，1.2Qbep流量工况下进行脉动幅值分析。在分析压力脉动时，压力脉动幅值用压力脉动系数Cp表示，计算式如下：

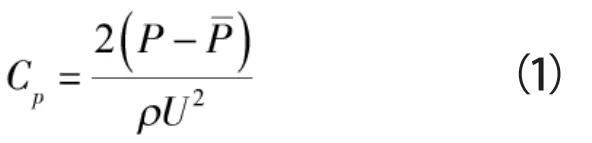
式中 P——监测点压力，kPa

ρ——水的密度，kg/m3

U——叶轮的圆周速度，m/s

各监测点时域如图4～6所示。为了分析各测点压力的时域变化，选取4个转动周期的脉动数据。周期N=t/T，t为所选点信号点采集时间，T为叶轮旋转一周的时间。横坐标把时间转化成叶轮旋转周期数表示。

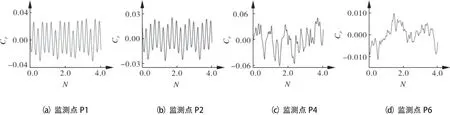
图4 1.2Qbep流量工况时各监测点的时域

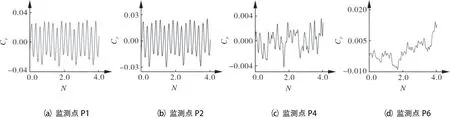
图5 Qbep流量工况时各监测点的时域

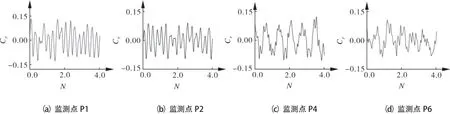
图6 0.3Qbep流量工况时各监测点的时域

由图4～6可知，分别在0.3Qbep，Qbep，1.2Qbep流量工况下，P1，P2监测点压力与时间呈正弦波形，压力波动较为明显，这说明叶片对水流的扰动作用在水流进入叶轮前已经发生。在1个叶轮旋转物理周期内压力变化呈现4个波峰和4个波谷，与轴流泵叶轮的叶片数相对应，这与文献［2～4］所得结论相同。监测点P1，P2都位于进水流道出口处，在0～4T周期时小流量工况0.3Qbep下，监测点P1的压力脉动最大幅值为P2的1.49倍，最优流量工况Qbep时监测点P1的压力脉动最大幅值为P2的1.09倍，大流量工况1.2Qbep时监测点P1的压力脉动最大幅值为P2的1.13倍；大流量工况1.2Qbep时P1，P2监测点压力脉动最大幅值分别比最优流量工况下小17%和18.3%。在0.3Qbep流量工况时，监测点P1，P2在0.5T～1.0T和1.5T～2.0T周期内出现了小范围二次波峰的现象，原因应该是小流量工况时叶轮内部产生的局部回流所致。

因监测点P4，P6位于出水流道的渐扩段，已远离叶轮，总体脉动幅值较小。在0.3Qbep流量工况时监测点P4，P6的脉动最大幅值分别为P1的0.098倍和0.064倍；在Qbep流量工况时监测点P4，P6的脉动最大幅值分别为P1的0.089倍和0.226倍；在1.2Qbep流量工况时监测点P4，P6的脉动最大幅值分别为P1的0.159倍和0.284倍。出水流道渐扩段处监测点波形无明显规律，每个周期内都出现局部小范围的波动，原因是水流从导叶体流出后仍具有一定的速度环量，且出水流道扩散角较小，直接导致水流扩散不均匀，压力变化未呈现规律性。

3.3 压力脉动峰峰值分析

压力脉动信号是一个随机信号，随时间和流量的改变而改变，有的测点脉动具有一定的周期性方便分析，但大部分测点的波形无法用解析式表达，目前有很多学者偏向于按置信度计算混频的压力脉动峰峰值。峰峰值是指一个周期内信号最高值和最低值之间差的值，就是最大和最小之间的范围。它描述了信号值的变化范围的大小，用来表示脉动幅度的大小。

因物理模型试验选取4个周期内的压力脉动幅值，所以采样点数有限，为更加宏观地分析各监测点的脉动程度，对总体进行评估，统计了3个流量工况时P1，P2，P4，P6监测点97%置信度的峰峰值，如图7所示。从图7上可以看出P1，P2监测点的压力脉动峰峰值大于监测点P4和P6，以P1，P4为例，在0.3Qbep，Qbep，1.2Qbep流量工况下监测点P1的脉动峰峰值分别是监测点P4的14.419倍，9.504倍和5.852倍，原因是监测点P1，P2受叶轮旋转等因素影响，导致脉动峰峰值较大，因导叶体的扩压和弯管对水流运动方向的约束作用，水流经导叶体扩散后压力脉动峰峰值减低。在0.3Qbep流量工况下，由于小流量工况时叶片载荷增大，叶片压力面和吸力面压差增大，导致靠近叶轮的P1，P2监测点此时的峰峰值较大。出水流道处监测点P4，P6峰峰值从1.2Qbep到0.3Qbep流量工况时先减小后增大，最优流量时脉动峰峰值最小。

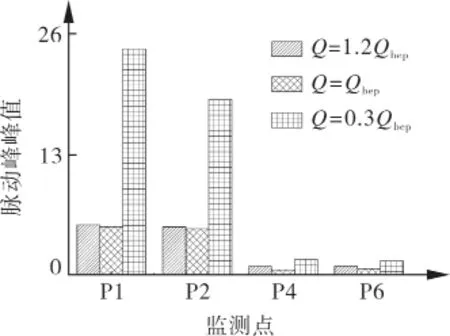
图7 97%置信度的脉动峰峰值分析

3.4 压力脉动信号各监测点频谱图分析

对采集到的压力脉动信号进行快速傅里叶变换（FFT）以分析频谱规律。为便于分析，频率以转频倍数表示：

式中 F——脉动数据经过FFT变换后对应的频率，Hz

n——转速，r/min

压力差：

式中 ΔP——频谱图中的压力变化，Pa

P——时均压力，Pa

各流量工况时进水流道出口段监测点的时域数据经傅里叶变换后的频谱如图8所示。从图8（a），（b）可知，P1，P2压力脉动的主频以叶片通过频率（4倍转频）为主。在0.3Qbep流量工况下，主频压力幅值较大，原因是泵内湍流强烈的不规则运动，此时低于4倍转频的低频脉动信号占主体，这与叶片载荷与小流量时叶轮的回流有一定的关系。1.2Qbep流量工况和最优流量下主频幅值相近，随着流量减小，主频脉动幅值不断增大，0.3Qbep流量工况下压力脉动幅值约是Qbep和1.2Qbep流量工况的2倍。出水流道渐扩段监测点P4，P6的压力幅值变化较大，但总体值偏低，监测点P4最大值仅为0.125kPa，监测点P6最大值为0.111kPa，出水流道渐扩段监测点P4，P6的脉动频率受转频的影响未呈现明显规律性。在最优流量工况时，监测点P4、P6脉动幅值均低于0.3Qbep，1.2Qbep流量工况时两监测点的脉动幅值，主频对应的压力幅值随流量的减小先减小后增加，在最优流量时最小，此时低频脉动信号较多。

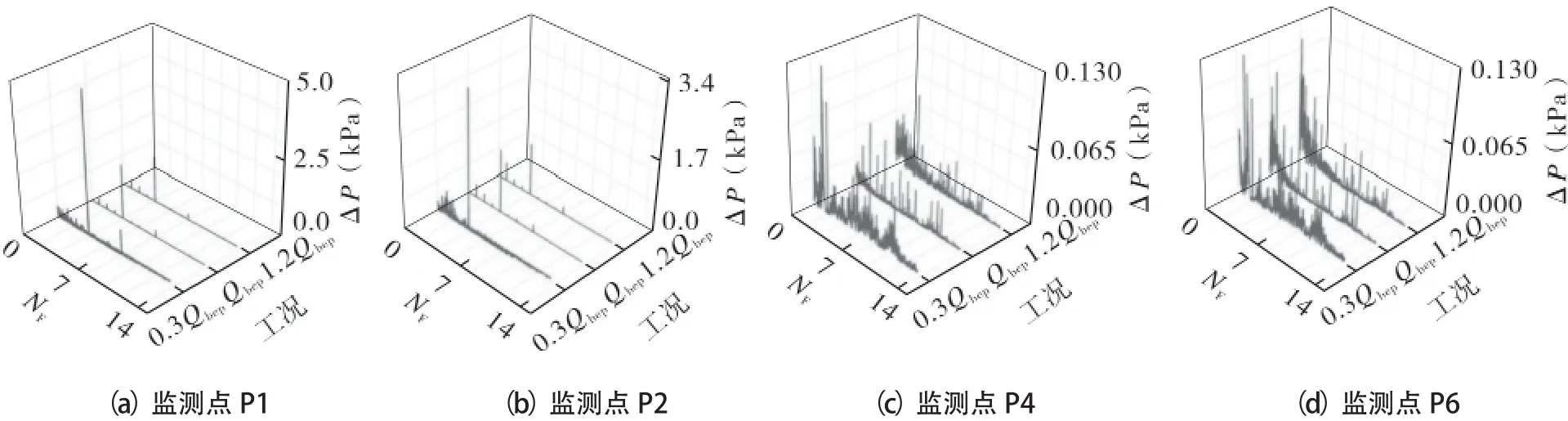
图8 各监测点在不同流量工况下的频谱

为进一步分析进水流道出口处监测点脉动主次频对应幅值的关系（定义此时主频为叶片数×转频，次频为转频的倍数），现将监测点P1，P2主次频进行分析。如图9所示，因在0.3Qbep流量工况时脉动幅值较大，应避免选择在小流量工况下运行。监测点P1，P2同属于进水流道出口处，且处于同一截面所对应的管壁上，但在1倍转频处脉动幅值却有很大差别。原因是水流流经肘型进水流道弯曲段后迅速改变方向并加速，在线性减缩段内，由于惯性力的强烈作用，较大的水流速度开始出现在流道外侧壁附近导致内外侧流速不同。可知监测点处于同一截面所对应的壁面处，由于水流流速的不同，对不同边壁的冲击力的差别，压力脉动幅值也不尽相同，该规律有待进一步分析。

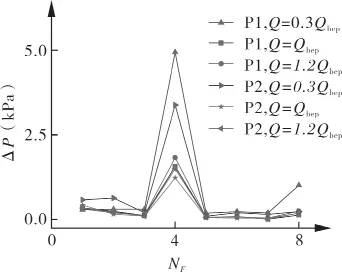
图9 进水流道出口处监测点主次频幅值

4 结论

（1）进水流道出口处各监测点的压力随时间呈正弦波形，一个物理周期内波峰波谷数与叶片数相同，进水流道出口处各监测点压力脉动幅值随流量增大而增大。出水流道渐扩段处监测点波形无明显规律，总体幅值较小，每个周期内均出现局部小范围的波动，原因是水流从导叶体流出后仍具有一定的速度环量，且出水流道扩散角较小，直接导致水流扩散不均匀，压力变化未呈现规律性。

（2）进水流道出口处监测点脉动主频为146.67Hz，主次频均为转频及其谐频，1.2Qbep流量工况和Qbep流量工况时主频幅值相近，随流量减小，主频脉动幅值不断增大，0.3Qbep流量工况下压力脉动幅值约是Qbep，1.2Qbep流量工况的2倍。

（3）因出水流道测试段远离叶轮与导叶体，转频对压力脉动的影响未发现规律性，随流量减小，主频对应的脉动幅值先减小后增大，在最优流量时最小，此时脉动频率以低频信号为主。立式轴流泵模型泵装置偏离最优流量运行时，压力脉动幅值增大。因此应尽量选择在最优流量工况附近运行。

［1］ 刘超.水泵及水泵站［M］.北京：中国水利水电出版社，2009.

［2］ 王福军，张玲，张志民.轴流泵不稳定流场的压力脉动特性研究［J］.水利学报，2007，38（8）：1003-1007.

［3］ Desheng Zhang，Dazhi Pan，Yan Xu，et al.Numerical investigation of blade dynamic characteristics in an axial flow pump［J］.Thermal Science，2013，17（5）：1511-1514.

［4］ 杨帆，刘超，汤方平，等.S形下卧式轴伸贯流泵装置叶片区压力脉动特性研究［J］.流体机械，2015，43（1）：16-22.

［5］ 汤方平，张丽萍，付建国，等.轴流泵内部压力脉动数值预测及分析［J］.排灌机械工程学报，2013，31（10）：835-838.

［6］ Khalifa A E，Al-Qutub A M，Ben-Mansour R.Study of pressure fluctuations and induced vibration at bladepassing frequencies of a double volute pump［J］.Arabian Journal for Science and Engineering，2011，36（7）：1333-1345.

［7］ 姚捷，施卫东，吴苏青，等.轴流泵压力脉动数值计算与试验［J］.农业机械学报，2013，44（1）：120-124.

［8］ 姚志峰，王福军，肖若富，等.双吸离心泵吸水室和压水室压力脉动特性试验研究［J］.水利学报，2012，43（4）：473-479.

［9］ Wang K，Liu H，Zhou X，et al.Experimental research on pressure fluctuation and vibration in a mixed flow pump［J］.Journal of Mechanical Science and Technology，2016，30（1）：179-184.

［10］ 杨帆，刘超，汤方平，等.灌排双向立式泵装置内部水流压力脉动特性［J］.排灌机械工程学报，2011，29（4）：316-321.

［11］ 施卫东，张光建，张德胜，等.入口非均匀流对轴流泵性能和压力脉动的影响［J］.排灌机械工程学报，2014，32（4）：277-282.

［12］ 石磊，张德胜，陈健.基于PANS模型的轴流泵叶顶空化特性［J］.排灌机械工程学报，2016，34（7）：584-590.

［13］ 张丽萍.非均匀来流条件下轴流泵内部压力脉动数值模拟研究［D］.扬州：扬州大学，2013.