基于复杂社会网络的微博营销理论

李 玲， 裴永珍， 梁西银， 李长国

(1.天津工业大学 计算机科学与软件学院，天津 300387;2.军事交通学院 基础部，天津 300161)

微博营销[1]，就是指以微博为平台或渠道进行的品牌推广、活动策划、形象包装、产品宣传等一系列营销手段，个人或者企业利用更新自己的微型博客向微博在线用户传播产品信息，树立良好的产品形象，每天更新内容来发布大家感兴趣的话题，这样来达到营销的目的.

对于复杂网络而言，钱学森给出了严格的复杂网络定义：即具有自组织、自相似、吸引子、小世界、无标度中部分或者全部性质的网络称为复杂网络.简而言之，复杂网络即为呈现出高度复杂性的网络[2].其复杂性主要表现在以下几个方面：1)结构复杂.表现在节点数目巨大，网络结构呈现多种不同特征.2)网络进化.表现在结点或连接的产生与消失.例如world-wide network，网页或链接随时可能出现或断开，导致网络结构不断发生变化.3)连接多样性.结点之间的连接权重存在差异，且有可能存在方向性.4)动力学复杂性.结点集可能属于非线性动力学系统，例如结点状态可随时间发生一些复杂变化.5)结点多样性.复杂网络中的节点可以代表任何事物.例如，人际关系构成的复杂网络结点代表单独个体，万维网组成的复杂网络结点可以表示不同网页.目前，复杂网络研究的内容主要包括：网络的几何性质，网络的形成机制，网络演化的统计规律，网络上的模型性质，以及网络的结构稳定性，网络的演化动力学机制等问题.其中在自然科学领域，网络研究的基本测度包括：度(degree)及其分布特征，度的相关性，集聚程度及其分布特征，最短距离及其分布特征，介数(betweenness)及其分布特征，连通集团的规模分布.

网络中少数称之为Hub点的结点拥有极其多的连接，而大多数结点只有很少量的连接(即度比较小或非常小)，而这些少数的Hub节点对网络的运行起着主导作用，这就是无标度网络.从广义上来说，无标度网络的无标度性是描述大量复杂系统整体上严重不均匀的一种内在性质，而无标度网络和小世界网络的最大区别就是他们的度分布的差别.

鉴于微博营销的各种优势和时代性，很多学者对此已经做过相关的讨论和研究.Daley和Kendall[3]提出了第一个谣言传播数学模型DK模型.Maki和Thomson[4]在DK模型上进行了传播规则的修改，构建了MT模型.但有一点值得提出的是，DK模型和MT模型均未考虑到网络的拓扑结构对谣言传播的影响.之后，Moreno[5]等人开始对网络中的谣言传播人群进行分类，将人群分为无知者(Ignorant)、传播者(Spreader)、免疫者(Stifler)三类.M.Nekovee和Y.Moreno[6]等人对复杂社会网络中的谣言传播进行了理论研究，并建立了含有潜伏机制和遗忘机制的SIR模型.上海工程技术大学管理学院的张志花、夏志杰等人[7]提出了基于唤醒机制的微博谣言传播模型，在模型中加入了冬眠者，考虑到了领袖传播者对冬眠者的唤醒作用.但是该文章仅考虑到了均匀网络中领袖传播者对冬眠者的唤醒作用，并未考虑到实际上微博是属于很典型的非均匀网络中的无标度网络的那一类型的，即微博网络中结点的度是服从幂率分布的.因此本文此基础上进一步考虑微博的实际网络拓扑结构，对模型进行了相应完善，从而构建出更加符合实际意义的数学模型.

我们基于SIR传染病模型和之前微博谣言模型相关理论[8]构建出基于唤醒机制的微博信息传播模型，并给出相应的平均场方程.我们研究了各个群体的数量随时间的变化规律，通过控制参数的方法(企业采取相应实际措施)，从而更好地在微博平台上展开营销活动.

1 微博平台信息传播的一般模型

本文对模型是这样来定义的.首先，假设现如今微博用户注册总人数是N个，微博网络是一个封闭且存在N个节点的无标度网络，每个节点代表一个可传播信息的用户，且节点总数N不变，信息是有向传播的，这些都是研究前提[9].考虑到冬眠者遇领袖传播者有可能被唤醒从而转化为传播者，我们提出新的信息传播模型如图1所示.用户群可分为四类，分别是无知者，传播者，潜伏者，冬眠者.无知者即为对企业或个人所发布的微博营销信息一无所知、毫不知情的人.在信息传播初期，绝大部分人都是处于这种状态的，很容易理解.传播者即为那些知道了这条信息并且去向外界转发或者传播的一类人.很显然，这一类人在营销信息的传播过程重扮演着极其重要的角色.潜伏者是指对此条信息知情，但是却不再转发或者传播的一类人.冬眠者是指这样一类原本处于传播者状态的人，由于其他微博信息的干扰而对此条信息暂时性失忆，或者对此条信息不感兴趣，但由于领袖传播者的存在，会重新激起这类人的转发或传播兴趣，从而再一次成为传播者.模型中各个参数的具体含义如表1.

表1微博信息传播模型图1参数含义

参数参数含义λ无知者接触传播者之后,一部分无知者转化为传播者的速率α传播者接触免疫者之后,对此条信息失去兴趣从而转化为免疫者的速率β传播者由于自身忘记所传信息,从而转化为冬眠者的速率δ冬眠者遇到“领袖传播者”并被其唤醒的速率(即唤醒率)

过程1：当无知者接触传播者之后，无知者对此条信息暂时忘记或者完全不感兴趣，此刻，他由无知者变为冬眠者(在这里本文没有对此项概率参数进行研究)；若要传播信息，那么就以的速率变为传播者.

过程2：当传播者忘记所传信息，从而以β的速率转变为冬眠者；另一方面，当传播者接触免疫者时，对此条信息失去兴趣从而以α的速率转变为免疫者.

过程3：当冬眠者接触领袖传播者时，此时他被唤醒，然后便以δ的速率变为传播者.

图1所示的流程图即为该数学模型的最形象化描述.

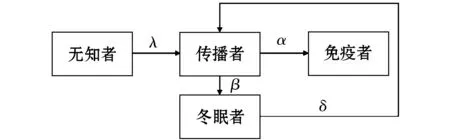
图1 流程图

信息传播过程：

1)当一个无知者遇到一个传播者时，可以有如下两种选择：1、以λ的速率转化为传播者；2、无知者对此条微博信息毫无兴趣，或者辨不出真假，或者忘记了，然后以某一速率转化为冬眠者.

1.2.3 测量指标及图像分析 在矢状面基础平面上沿耻骨联合后下缘做一条水平参照线，分别测量静息状态及Valsalva动作时膀胱颈至参照线的垂直距离，二者间距即为BND。膀胱颈位于参考线头侧，定义为参考线上，膀胱颈距离参考线测值为正数(+)，(图1A)。Valsalva动作时膀胱颈向尾侧移动越过参考线位置，定义为参考线下，膀胱颈距离参考线测值为负数(-)(图1B)。

2)当一个传播者遇到一个免疫者时，也可以有如下两种选择：1、传播者受到免疫者的蛊惑，以α的概率转化为免疫者；2、传播者对此条微博信息暂时性失去兴趣，或者由于传播者本身大量的刷微博行为，导致他暂时性忘记，从而以β的概率转化为冬眠者.

3)最后这一点是最关键的.之前无数研究证明，微博的网络拓扑结构是服从幂律分布的.和均匀网络有所不同的是，网络中节点之间的度相差很大，在大家的度原本都差不多的前提下，突然冒出少数一些度很大很大的节点，这就是我们的领袖传播者.比如明星、知名媒体、权威人士、商界精英等，他们的观点在很大程度上是可以影响多数信任或者崇拜他们的人的观点的，甚至可以引领时代潮流.因此，当冬眠者遇到这些领袖传播者之后，会有极大的被唤醒的可能，从而以δ的概率转化为传播者，继续对此条微博信息进行传播.

2 建立平均场方程

统计物理学的平均场理论[10]是一种研究系统热力学性质的近似方法.它起源于物理学中对大量对等物体相互关系的研究，也就是用一个作用来等价地刻画所有其他物体对该物体的作用，简化分析过程.物体相互作用的过程可以用马尔可夫链分析，但当物体状态较多、物体数量巨大时马尔可夫链模型就相当复杂，难以求解.而用平均场模型就能很好地对这个过程进行近似，且效果不错.尽管由平均场理论所得到的结果是近似的，但由于它是基于对问题的高度概括和抽象，因而由它所推导出来的结论更加具有普适的意义.对于一个不为人所熟悉的复杂系统，平均场理论往往是揭示它本质属性的突破口，因此它成为了研究复杂网络系统的一个有力工具，在复杂系统的各种研究方法中占有重要的地位.

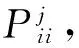
把在t时刻j结点的邻居中所有处于传播者状态的结点数量记为g(t)，在某一固定时刻，g(t)即变为了一个常量，Δtλ是j结点接触所有处于传播者状态的结点中的一个传播者结点时，j变为传播者结点的概率，那么j结点在接触完所有传播者结点后仍保持无知者状态的概率即为(1-Δtλ)g，记作:

(1)

假定结点j一共有k个邻居结点，那么g就是满足二项分布的一个随机变量，用概率可表示为:

(2)

其中:θ(k,t)是某一个度为k的结点在t时刻能够认识(表现在图上即为连接)一个传播者的概率.对于度为k的一类结点，这个概率值是相同的，故言之，对于不同度的结点，这个概率值显然是不同的.θ(k,t)g也可以如下表示:

(3)

(4)

(ρs(k′,t))k(1-δΔr))

(5)

下面分别用ρi(k,t+Δt)、ρs(k,t+Δt)、ρr(k,t+Δt)、ρl(k,t+Δt)表示在t+Δt时刻无知者I、传播者S、免疫者R、冬眠者L四类人的数量在种群总人数中所占的比例.上文中已经得到了I在接触完S之后保持I状态不变的概率以及S在接触完S和R之后的概率，那么在经历了Δt时间段之后，我们也可以很容易得到ρi(k,t+Δt)、ρs(k,t+Δt)、ρr(k,t+Δt)、ρl(k,t+Δt)表示在t+Δt四者的密度占比，求得结果如下：

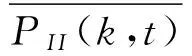
(6)

ρl(k,t+Δt)=ρl(k,t)+βρs(k,t)-δρl(k,t)

(7)

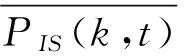
(8)

(9)

对上式变形，便得到方程组，如下：

(10)

3 Matlab仿真

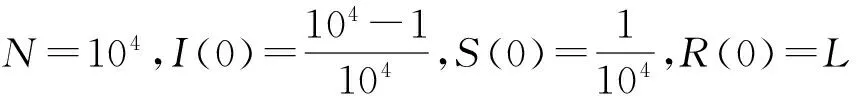
3.1 四类人所占比例随时间的变化

由图2可以看出，随着时间的推移，无知者的数量(表现在图中即为密度)在不断减少，并且在某一段时间内其数量迅速减少，最终缓慢地趋向于零.传播者在信息传播前期其数量不断增大，之后随着时间推移慢慢趋于零，最终消失.免疫者一开始数量逐渐增大，然后在信息传播的末期，由于大部分人已经对该信息有所了解却不再去向他人传播，此时除了极少数对该信息依然处于无知者状态，剩下的便全都成为了免疫者.冬眠者的数量开始在不断增大，达到一定值的时候，慢慢降下来，最后其数量慢慢趋于平稳状态，这正是由于领袖传播者的唤醒作用所导致.以上分析就是这四类人的数量变化.

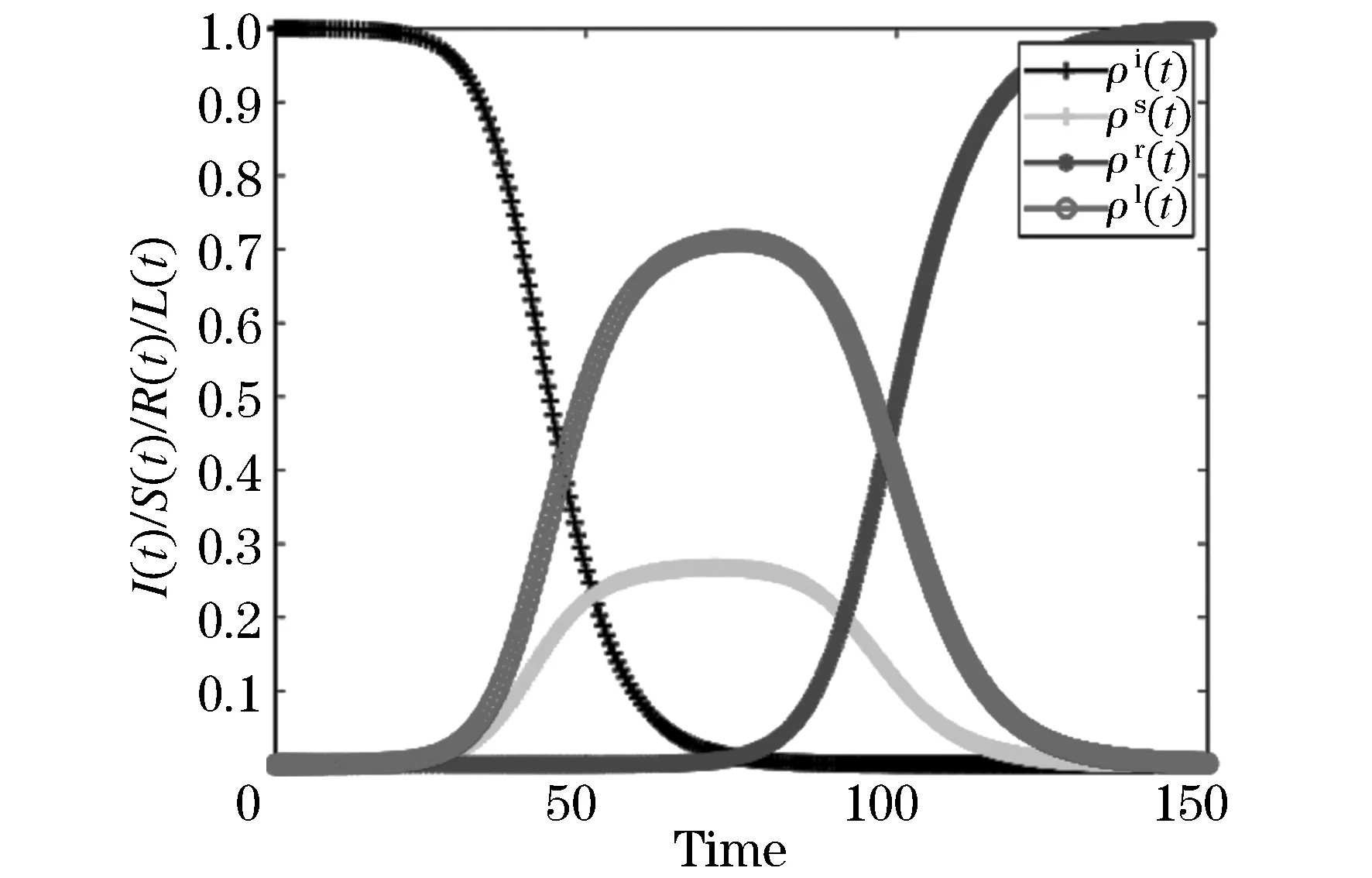
图2 四类人的密度时间的变化

3.2 唤醒率δ仿真与分析

本文根据实际情况加入了对唤醒率这个参数的考量，通过δ来衡量领袖传播者对冬眠者的唤醒力.本节通过Matlab来模拟唤醒率对现实中这三类人的数量以及变化速度的影响.在图3中，均设定λ=0.8，α=1，β=0.8，=15，唤醒率δ分别等于0.6，0.7，0.8.由图3(A)可知，唤醒率δ越大，微博信息初期传播速度越快(表现在图中即为斜率)，达到峰值时的传播者数量越大，整个信息传播所经历的时间越短，结束的越快，从而在短时间内使得更多的无知者更快更高效地获得信息，进而提升此条信息传播的影响力.由图3(B)可知，唤醒率δ越大，传播者转变为免疫者的速度越快，此条信息最终所被熟知的人的数量越多，影响更加广泛.由图3(C)可知，唤醒率δ越大，传播者转变为冬眠者的速度越快，冬眠者所达到的峰值时的数量越少(因为δ增大时冬眠者被领袖传播者唤醒的数量会相应地增多).

图3 当δ取值分别为0.6，0.7，0.8时，三类人

4 结 语

本文根据传染病SIR模型，结合微博信息传播过程的实际情况，建立了信息传播模型.因为微博用户总是在“刷微博”，所以在浏览完一条微博推送消息之后，可能会因为之后浏览的其他微博信息而暂时忘记上一条信息，即此模型中冬眠者的存在.但由于微博社交网络拓扑结构是属于无标度网络(SF网络),故网络中有“领袖传播者”的存在.即当这条微博信息被“领袖传播者”再次转发时，会重新激起冬眠者对这条信息的转发欲望，这使我们的模型更加符合实际意义.然后应用概率论和微分方程的相关数学知识，给出了该模型的平均场方程.用Matlab对该模型进行仿真，了解模型中各个参数对微博信息传播速度及最终规模的影响，从而通过采取各种有效措施来加速微博信息传播，使微博营销更有效地进行.

[1] 张 晞．微博营销[J]．企业管理，2010(11)：84-87．

[2] 唐晓波，宋承伟.基于复杂网络的微博舆情分析[J]．情报学报，2012(11)：1153-1162．

[3] DALEY D J， KENDALLD J．Stochastic Rumours[J]．Journal of Applied Mathematics，1965，1(1)： 42-45．

[4] MAKI D P，THOMPSON M．Mathematical Models and Applications，with Emphasis on Social， Life， and Management Sciences[M]．Englewood Cliffs， New Jelsey： Prentice―Hall， 1974.

[5] MORENO Y，NEKOVEE M， PACHEOO A.Dynamics of Rumor Spreading in Complex Networks[J]．Physical Review E，2004，69(6Pt2)：066130．

[6] NEKOVEE M, MORENO Y．Theory of rumour spreading in complex social networks[J]．PhysicaA，2007，374(1)：457-470．

[7] 张志花，夏志杰．基于唤醒机制的微博谣言传播模型[J]．现代情报，2015，35(3)：28-33.

[8] PITTEL B．On a Daley-Kendall model of random rumours[J]．Journal of Applied Probability，1990，27(1)：14-27．

[9] BOCCALETTS，LATOE V, MORENO Y，etal．D-U.Complex networks：Structure and dynamics[J]．Physics Reports，2006，424(4)：175.

[10] GU J，LI W，CAI X．The effect of the forget-remember mechanism on spreading[J]．EuropeanPhysical Journal B，2008，62(2)：247-255．