海洋三维VC观测系统优化设计

安振芳，张 进，张建中

1.海底科学与探测技术教育部重点实验室，山东 青岛 266100 2.中国海洋大学海洋地球科学学院，山东 青岛 266100

0 引言

随着经济和社会的普遍发展，人类对能源的消耗与日俱增，煤、石油和天然气等常规能源储量逐日递减，因此迫切需要为我们的后代寻找可替代能源。众所周知，地球上70%的面积被海水所覆盖，海底蕴含着丰富的矿物能源，比如锰结核、热液矿床与天然气水合物等。据有关资料统计，全球天然气水合物总量大约相当于已探明传统化石燃料碳总量的两倍[1-2]。在标准状况下，单位体积天然气水合物可释放出160～180体积的天然气[3-4]。天然气水合物被认为是未来人类赖以生存和发展的高效清洁能源，受到世界范围内科研人员的普遍关注。

现今常规海洋三维地震勘探主要采用一船多缆或多船多缆的方法进行资料采集，在大多数情况下水平缆能够满足成像的基本要求。然而，对于深水崎岖海底或地下复杂构造，水平缆的成像精度却不够理想[5-6]。另外，在采集过程中不可避免地会受到多次波的干扰，且在处理阶段无法有效剔除。海洋垂直缆(vertical cable，VC)起源于海洋变偏移距垂直地震剖面(walkaway vertical seismic profiling，WVSP)，它是通过美国海军用于反潜作战而发展起来的一项技术[7]。海洋VC的底端固定在沉放于海底的锚上，顶端系在漂浮于海面的浮球上，以确保电缆能够处于垂直状态[8]。据报道[9]，1987年在墨西哥湾首次使用海洋VC进行了地震数据采集，用于盐丘侧翼砂岩储层的成像。1997年，Moldoveanu等[10]在墨西哥湾两个小的3D工区，在水平缆和装有无线电遥测系统的海洋VC之间进行了一次对比，结果显示，海洋VC衰减交混回响的能力更强，信噪比和分辨率更高。实践[11-15]证明，海洋VC可以识别自由表面多次波和虚反射，还可以对上行波和下行波进行波场分离，将下行波场经过处理后叠加到上行波场的能量中可以提高信噪比。此外，由于是多方位角采样，因此可以真正做到3D成像。与VSP相比，海洋VC具有激发点均匀、激发效率高、不受井位限制和成本相对低廉的优点。

观测系统设计在地震勘探中起着无可替代的作用，最佳观测系统不仅可以提高资料品质，还能够降低采集成本，因此有必要对观测系统进行设计、评价与优化。覆盖次数和照明分析是评价观测系统设计优劣的两个极其重要的指标。本文针对单VC和多VC的特点，分别设计了相应的观测系统，然后利用覆盖次数和照明分析对所设计的观测系统进行评价，最后根据评价结果优选出最佳设计方案。统计覆盖次数时我们采用射线追踪方法[16]来计算每个面元内的反射点数，覆盖次数与反射点数成正比关系。基于射线理论的照明分析方法[17-19]也同样是以反射点的疏密为参考值，面元内的反射点密集则照明能量强，反之面元内的反射点稀疏则照明能量弱。

1 波场随偏移距的变化特征

根据世界范围内已发现天然气水合物区的海水深度、天然气水合物稳定带厚度、似海底反射(bottom simulating reflection，BSR)埋深及地层速度，并参照我国南海西北陆坡研究区的地震层序划分[20-23]，我们建立了含天然气水合物的七层水平介质3D模型(图1)，模型参数如表1所示。该模型的海水深度为1 000 m，目标层深度为1 900 m，模型尺寸为100 000 m×100 000 m。VC的坐标为(50 000 m，50 000 m)，接收点间距为6.25 m，共161个接收点。

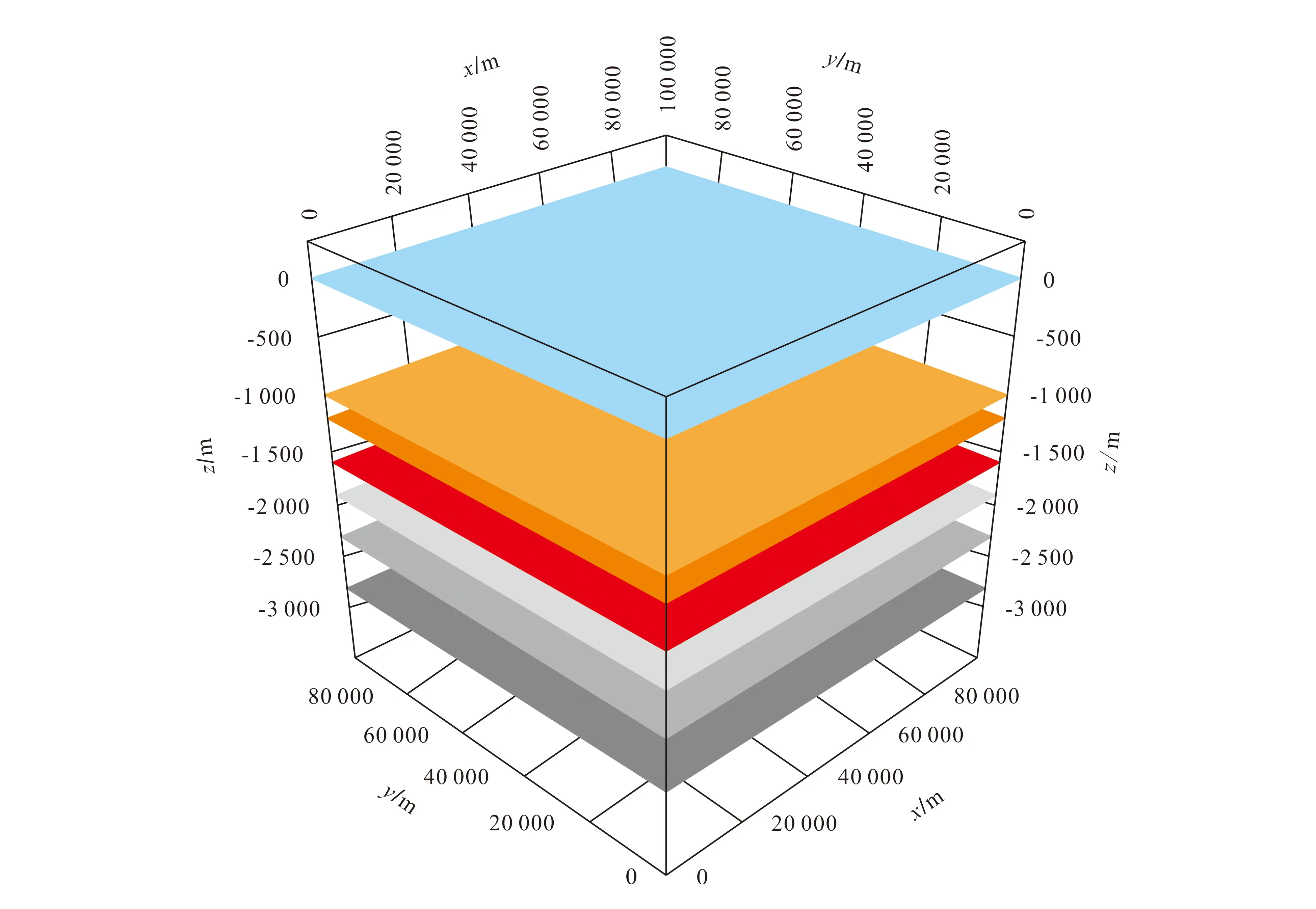
图1 含天然气水合物的七层水平介质3D模型Fig.1 Three dimensional model constituted by seven horizontal layers containing natural gas hydrate

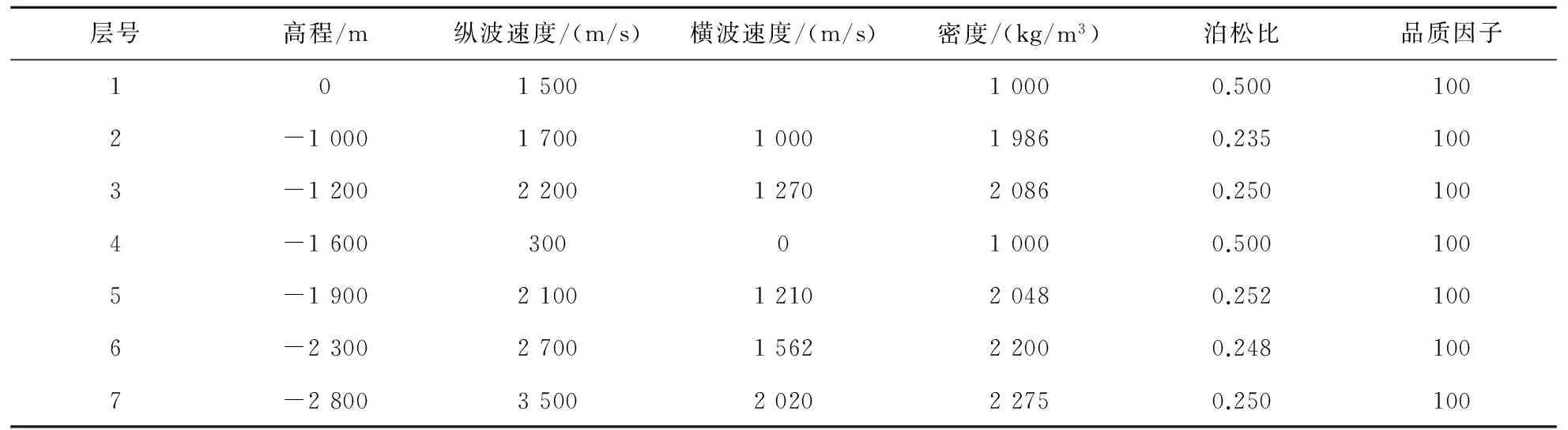
层号高程/m纵波速度/(m/s)横波速度/(m/s)密度/(kg/m3)泊松比品质因子10150010000.5001002-10001700100019860.2351003-12002200127020860.2501004-1600300010000.5001005-19002100121020480.2521006-23002700156222000.2481007-28003500202022750.250100

正演模拟方法主要有射线追踪法[24-25]和波动方程法[26-27]。射线追踪法具有运行速度快、运算效率高等特点，而且特别适用于模拟自由表面多次波和虚反射，因此采用射线追踪法合成地震记录。图2是表1所示模型在偏移距分别为1 000 m、4 000 m、7 000 m和10 000 m时模拟一次波的合成记录(暂不考虑临界角的影响)，其中除直达波以外的其余6个同相轴分别对应表1中7个地层的6个界面，地层1与地层2之间为界面1，地层2与地层3之间为界面2，以此类推。当偏移距为1 000 m时(图2a)，各界面同相轴与地层顺序一致，由于第4层是游离气层，从图中可以清晰地看出该层顶界面同相轴极性发生了反转；当偏移距为4 000 m时(图2b)，界面1、界面2、界面3与直达波同相轴相互交叉、缠绕；当偏移距为7 000 m时(图2c)，界面4与界面6同相轴相互交叉、合并；当偏移距为10 000 m

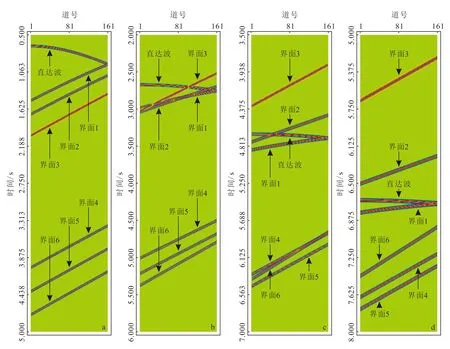
a、b、c、d偏移距依次为1 000 m、4 000 m、7 000 m、10 000 m。图2 VC在不同偏移距的一次波合成记录Fig.2 Synthetic primary record of vertical cable in the case of different offset

时(图2d)，虽然各界面同相轴相互之间不交叉，但地层顺序发生了变化，从上到下依次为界面3、界面2、直达波、界面1、界面6、界面4和界面5。由此可见，随着偏移距的增大，同相轴会出现交叉现象，地层顺序也会发生变化。这是没有模拟多次波的合成记录，而实际中多次波非常发育，波场会更复杂难辨。因此，在设计观测系统时偏移距不宜过大，以上下行波场容易识别为宜。

2 单VC激发观测系统

根据单条VC的特点以及激发点组合图案的不同，单VC激发观测系统可设计为“平行形”、“正交形”、“斜交形”、“轮辐形”、“螺旋形”和“圆环形”，如图3所示。

由图3可见，“平行形”、“正交形”、“斜交形”和“轮辐形”激发观测系统都属于“直线型”观测系统，而“螺旋形”和“圆环形”激发观测系统则属于“曲线型”观测系统。在“直线型”观测系统中，“平行形”、“正交形”和“斜交形”激发观测系统又可进一步划分为一类，“正交形”激发观测系统可看成是由“平行形”激发观测系统旋转90°后叠加而成，而“斜交形”激发观测系统则可看成是由“正交形”激发观测系统旋转45°后叠加而成。

从“平行形”到“正交形”再到“斜交形”激发观测系统，面元覆盖次数近似成倍增加，反射点空白带逐渐减少，反射点分布越来越均匀，观测方位角愈来愈丰富。从方位角分布来看，“曲线型”观测系统比“直线型”观测系统的方位角富裕。

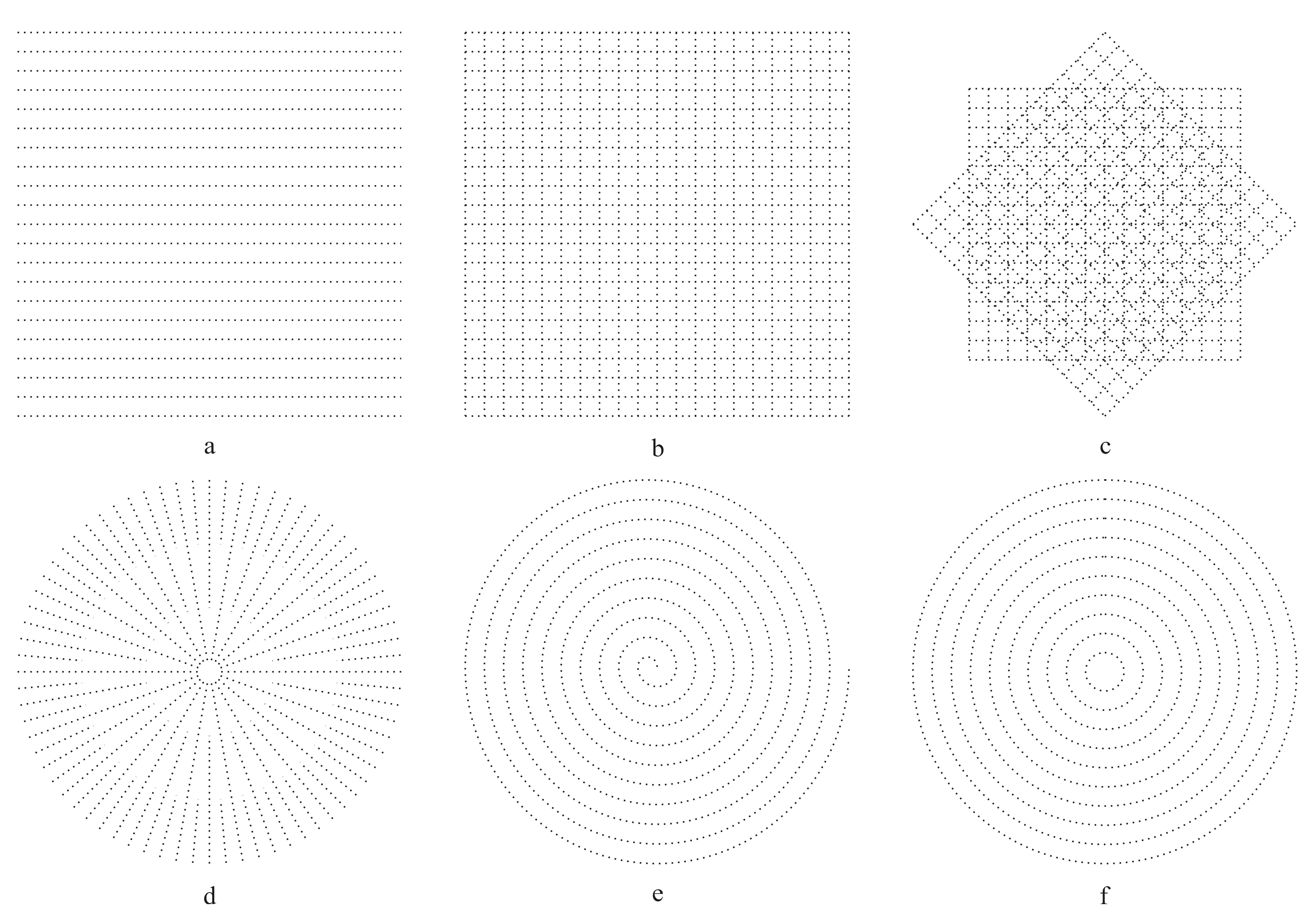
a.平行形；b.正交形；c.斜交形；d.轮辐形；e.螺旋形；f.圆环形。图3 单VC激发观测系统示意图Fig.3 Geometry in the case of single vertical cable

2.1 两种改善面元覆盖次数的效果对比

面元覆盖次数由激发点数和接收点数共同贡献，当单VC接收点数一定时，可以通过增加激发点数的方法以满足覆盖次数的要求。增加激发点的方法可以分为两种情况：其中一种情况是当激发面积一定时，通过减小激发点间距和激发线间距，即增大激发点密度的方法来增加覆盖次数；另外一种情况是当激发点间距和激发线间距一定时，通过增大激发面积，即增加激发线条数和激发线长度的方法来增加覆盖次数。下面首先看第一种情况下的面元覆盖次数分布。

采集表1的模型，第一条激发线的第一个激发点坐标为(48 000 m，48 000 m)，最后一条激发线的最后一个激发点坐标为(52 000 m，52 000 m)，激发面积为4 000 m×4 000 m。在激发面积一定的情况下，设计不同的激发点间距与激发线间距(表2)，观察不同设计方案观测系统的面元覆盖次数(图4)。注意：接收点数是指每条接收线上的接收点数，激发点数是指每条激发线上的激发点数(下同)。

从图4可以看出，随着激发点间距的缩小，反射点空白带逐渐减少直至消失。由于海水深度有限，致使接收点数受到限制，而增加VC条数意味着高昂成本的增加；因此当激发面积一定时，只能通过加密激发点以达到满次覆盖的要求。从图4还可以看出，激发线间距等于激发点间距时的覆盖次数分布情况(图4b、d、f)要好于激发线间距大于激发点间距时的覆盖次数分布情况(图4a、c、e)。

上面已经讨论了第一种情况，且其增加覆盖次数的效果很好，下面再来分析第二种情况下的覆盖次数分布。设计了4个方案，激发面积分别为4 000 m×4 000 m，6 000 m×6 000 m，8 000 m×8 000 m，10 000 m×10 000 m。4个方案的面元覆盖次数分布情况如图5所示。

从图5可以看出，随着激发面积的增大，观测面积随之增大，面元覆盖次数有所增加，但增加的幅度甚微，当激发面积增大到10 000 m×10 000 m时，目标层仍残存反射点空白带。因此当观测面积一定时，采用增加激发点密度的方法对面元覆盖次数的改善效果要好于采用增加激发面积的方法对面元覆盖次数的改善效果。

由表5说明，土样1土壤中添加2%骨炭(A)化学修复剂时土壤中的重金属锌、铅、铬、铜、砷、镉含量均有所下降，其中在种有马铃薯的土壤区域主要污染物锌含量下降幅度最大，下降值为90.1mg/L。在种有油菜和马铃薯的土壤区域主要污染物砷含量下降幅度最大，最大值为1.0mg/L。

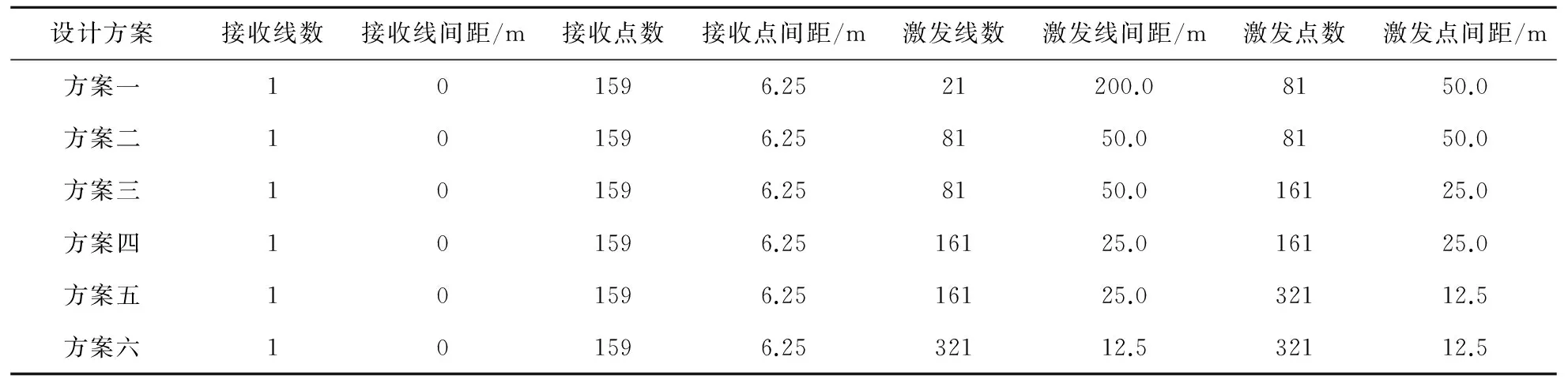
表2 不同空间采样间隔观测系统设计方案

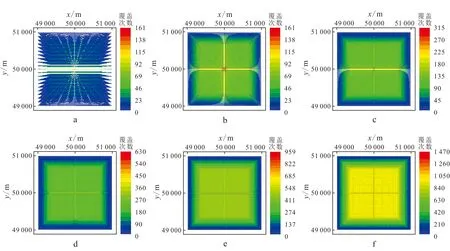
a.方案一；b.方案二；c.方案三；d.方案四；e.方案五；f.方案六。图4 不同空间采样间隔观测的面元覆盖次数Fig.4 Bin fold of geometry with different spacial sampling interval

2.2 地层倾角对目标层照明的影响

当地层存在倾角时对目标层的照明会发生哪些变化呢？为了得到问题的答案，我们设计了一个目标层倾角为15°的三层水平介质模型(图6)。目标层深度为2 500 m，目标层方位角为90°，目标层倾斜旋转所绕的定点坐标为(50 000 m，50 000 m)，令目标层倾角在0°、5°、10°、15°之间变化，分析不同倾角时的目标层照明情况，结果如图7所示。

由图7可见，当目标层倾角为0°时(图7a)，目标层照明强度关于VC均匀、对称分布。当目标层存在倾角时(图7b、c、d)，目标层照明区域呈梯形，梯形的上底相对于VC位于目标层的下倾方向，梯形的下底相对于VC位于目标层的上倾方向。随着目标层倾斜角度的增加，相对于VC位于目标层上倾方向上的观测面积逐渐增大，相对于VC位于目标层下倾方向上的观测面积逐渐减小，目标层照明强度分布关于VC不均匀、亦不对称，照明强度从上倾方向到下倾方向逐级递增，随着倾斜角度的增加照明强度逐渐向VC位置聚焦。

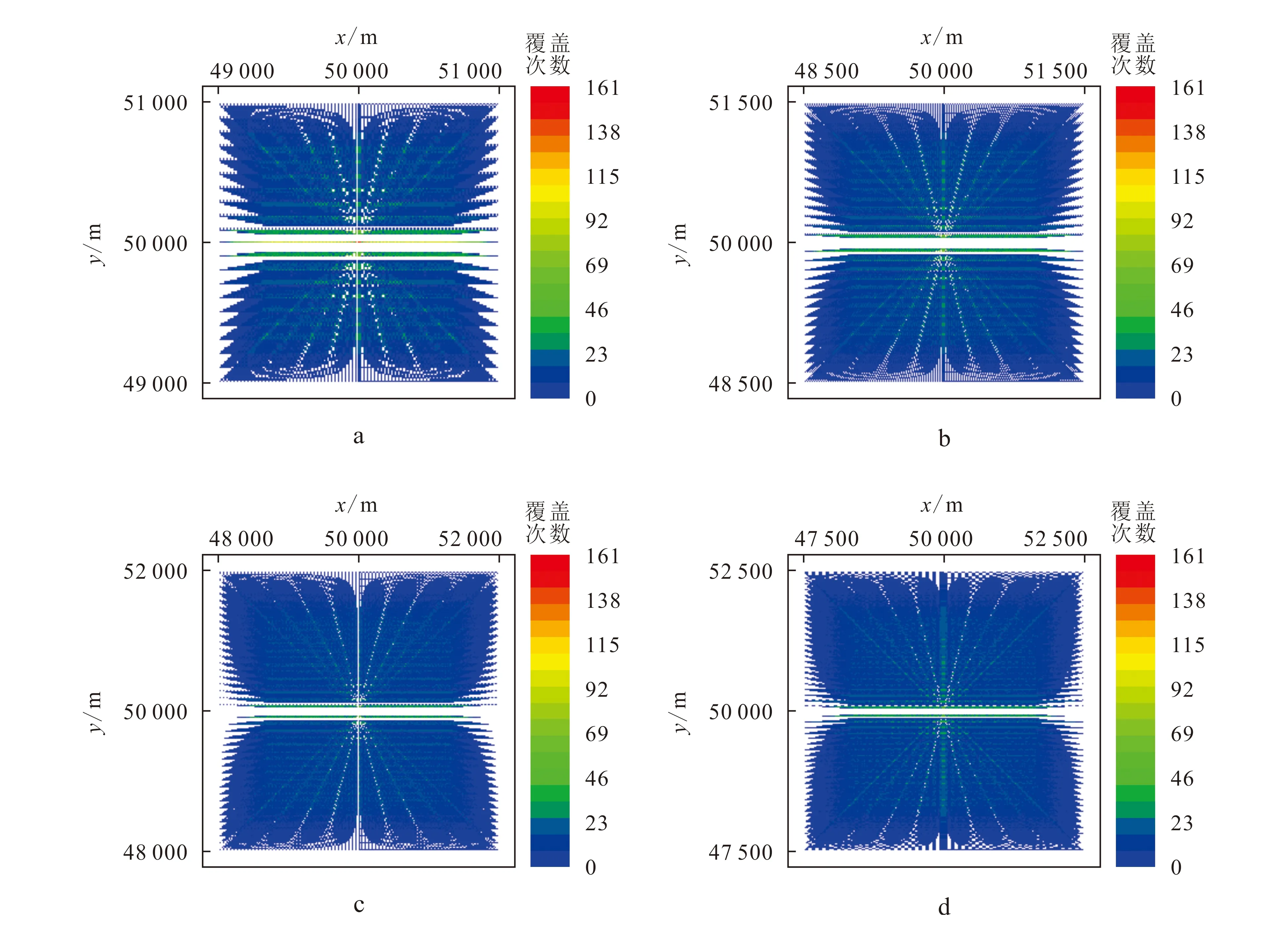
a、b、c、d激发面积依次为4 000 m×4 000 m、6 000 m×6 000 m、8 000 m×8 000 m、10 000 m×10 000 m。图5 不同激发面积观测的面元覆盖次数Fig.5 Bin fold of geometry with different shot area

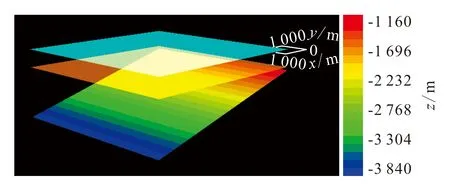
图6 目标层倾角为15°的三层水平介质3D模型Fig.6 Three dimensional model constituted by three horizontal layers when the target inclination is equal to 15°

下面以倾角为15°时的目标层为例，分析观测系统如何设计才能补偿因存在倾角而导致的目标层照明范围的损失。图8a是激发面积为4 000 m×4 000 m时的目标层照明情况，激发原点坐标为(48 000.0 m，48 000.0 m)，共321条激发线，每条激发线上有321个激发点，长划线矩形框表示倾角为0°时的目标层照明范围。首先保持y方向上的激发线数固定不变，激发原点坐标仍为(48 000.0 m，48 000.0 m)，只增加x方向上的激发点数，当每条激发线上的激发点数增加到483个，即激发面积为6 025 m×4 000 m时，x方向上的照明范围恰好填充到长划线矩形框的右边界(图8b)。然后再增加y方向上的激发线数，激发原点坐标为(48 000.0 m，47 612.5 m)，当激发线数增加到383条，即激发面积为6 025 m×4 775 m时，y方向上的照明范围恰好填充到长划线矩形框的上下边界(图8c)。

2.3 背斜与向斜目标层照明分析

图9a、b分别是背斜和向斜模型，目标层底部高程分别为-2 000 m和-2 500 m，长度与宽度均为2 000 m，高度均为500 m。以VC所在位置为圆心进行圆环形激发，最小环半径为50 m，最大环半径为2 000 m，环间距为50 m，激发点间距为25 m，每个环上的最小激发点数为18。

图10a、b分别为该观测系统对背斜与向斜目标层的照明情况，可以看出，当目标层为背斜时，只能观测到背斜的顶部，观测范围为以(50 000 m，50 000 m)为圆心、半径为150 m的圆形区域，其余一个环形区域则为观测盲区。当目标层为向斜时，观测区域可分为三部分，第一部分是以(50 000 m，50 000 m)为圆心、半径为62.5 m的圆形区域，第二部分是以(50 000 m，50 000 m)为圆心、分别以587.5 m和700 m为半径的环形区域，第三部分是以(50 000 m，50 000 m)为圆心、分别以825 m和1 000 m为半径的环形区域，其余两个环形区域则为观测盲区。

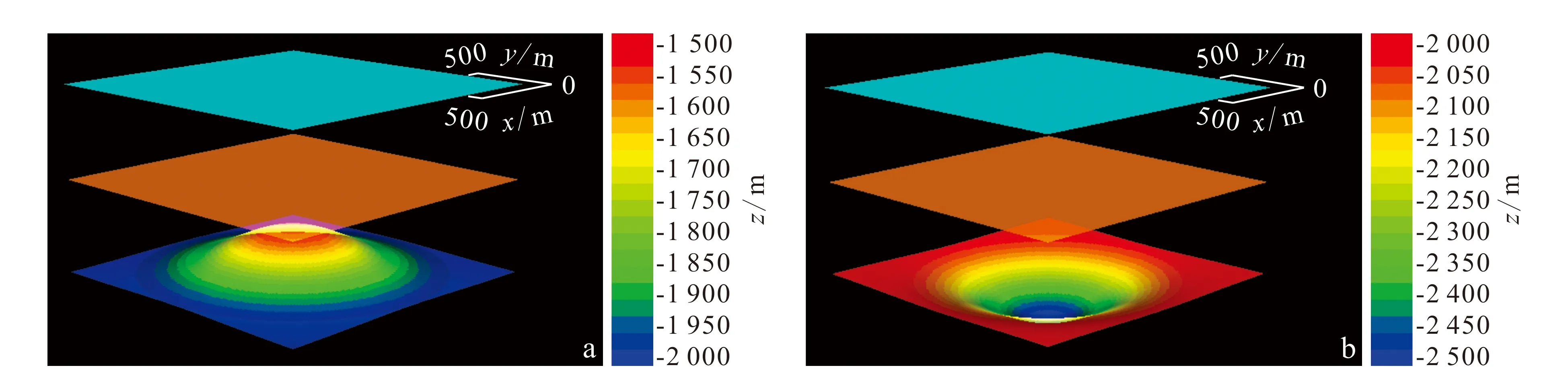
图9 背斜目标层(a)与向斜目标层(b)3D模型Fig.9 Three dimensional model constituted by anticline (a) or syncline (b)

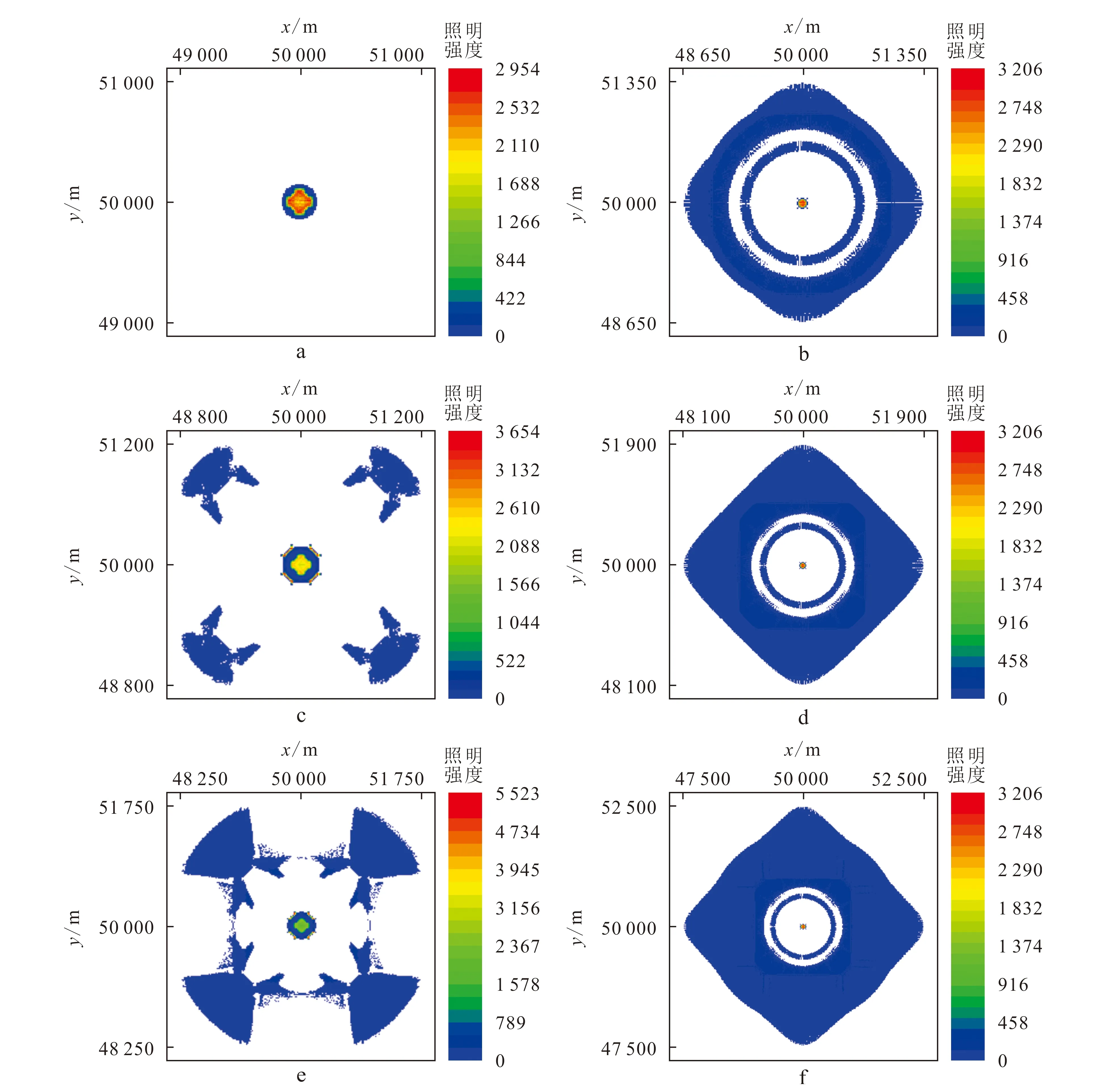
a、b. 最大环半径为2 000 m；c、d. 最大环半径为3 000 m；e、f. 最大环半径为4 000 m。图10 背斜(a、c、e)与向斜(b、d、f)目标层照明Fig.10 Illumination of geometry when the target is anticline or syncline

当最大环半径增大到3 000 m时(图10c、d)，对背斜的照明半径增加到187.5 m，对向斜的照明范围没有变化，增加的只是向斜边界外的区域；当最大环半径增大到4 000 m时(图10e、f)，对背斜的照明半径增加到212.5 m，观测到了背斜边界，对向斜的照明范围还是没有变化；当最大环半径增大到5 000 m时，对背斜的照明半径不再增加，对向斜的照明范围仍旧没有变化。因此，通过增大最大环半径来增加背斜和向斜照明范围的方法奏效甚微，即使将VC的位置任意移动也无法对背斜和向斜进行全面观测，这时就需要在以VC坐标为圆心的圆环上布设多条VC以补偿照明损失。

3 多VC接收观测系统

地质构造变化剧烈的复杂勘探区，单条VC接收无法得到地下沉积地层的有效反射。根据VC的数量及其相互之间的位置关系，我们设计了“n阶方阵”接收观测系统(图11)、“正N边形”接收观测系统(图12)和“圆环形”接收观测系统(图13)。

所谓“n阶方阵”接收观测系统，就是在等间距的n行n列的交点位置布设n2条VC，每相邻两行两列交点上的4条VC构成一个接收单元，共有(n-1)2个接收单元，所有这些接收单元组合在一起我们称之为接收区域，接收区域的面积称为接收面积。注意：这里的接收面积指的是由外围边界上2n+2(n-2)条VC所围成的自由表面面积，而并非我们通常所认为的这n2条VC实际所观测的地下反射界面面积(观测面积)。

采用表1的模型，观测系统设计方案如表3所示，4条VC的坐标见表4。4种设计方案的接收面积分别为1 000 m×1 000 m、2 000 m×2 000 m、3 000 m×3 000 m和4 000 m×4 000 m，每种设计方案的激发面积等于接收面积，选择“正交形”激发观测系统。注意：激发线数是指y方向上的激发线数。

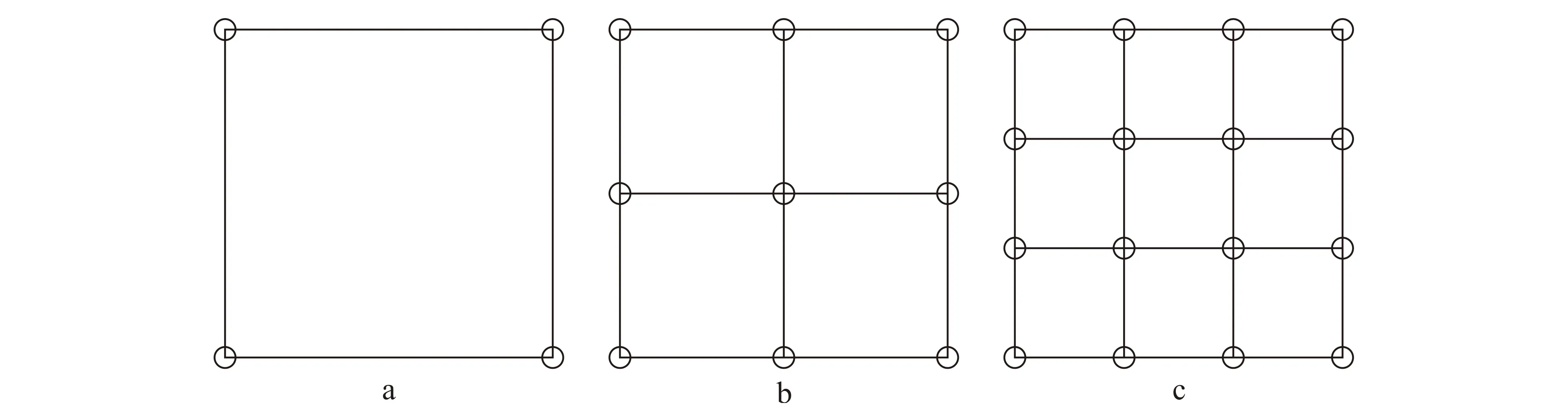
a. n=2；b. n=3；c. n=4。图11 “n阶方阵”接收观测系统Fig.11 Geometry of n order square matrix in the case of multiple vertical cable

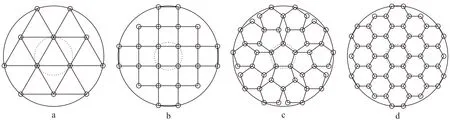
a. N=3；b. N=4；c. N=5；d. N=6。图12 “正N边形”接收观测系统Fig.12 Geometry of regular polygon in the case of multiple vertical cable

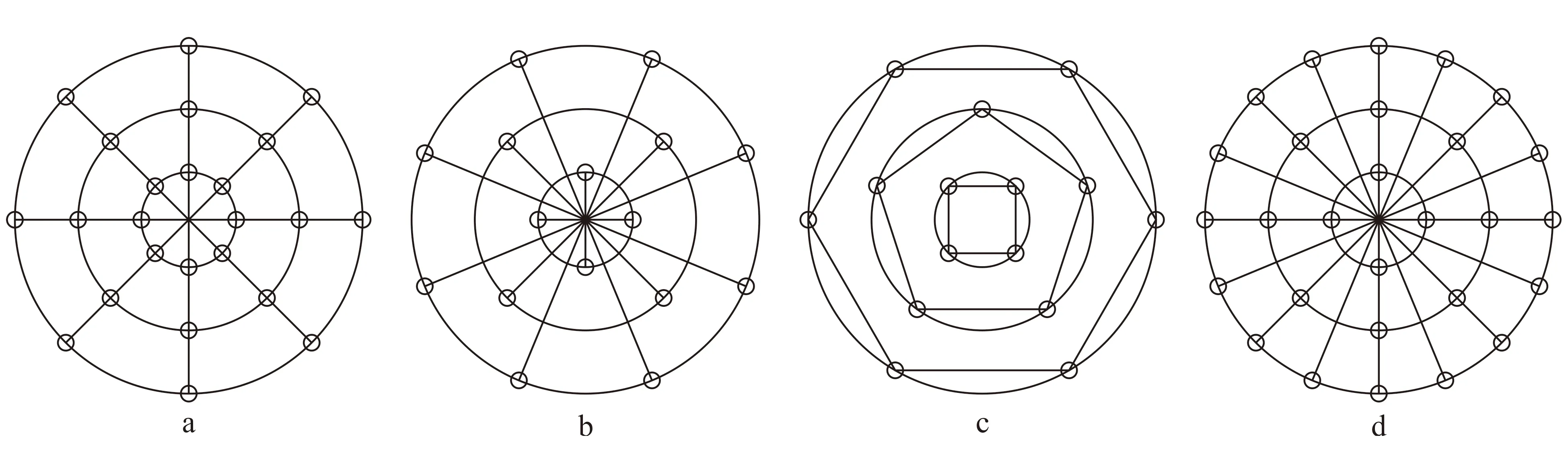
a.同一圆上的接收线间距相等，不同圆上的方位角相同、接收线条数相等、接收线间距不相等；b.同一圆上的方位角不相同、接收线间距相等，不同圆上的方位角不相同、接收线间距不相等；c.同一圆上的接收线间距相等，不同圆上的接收线条数不相等、外圆比内圆上接收线条数多；d.相邻两圆外圆方位角数是内圆的两倍，接收线条数亦是如此。图13 “圆环形”接收观测系统Fig.13 Geometry of rings in the case of multiple vertical cable

设计方案接收线数接收线间距/m接收点数接收点间距/m激发线数激发线间距/m激发点数激发点间距/m方案一410001596.2562008112.5方案二420001596.251120016112.5方案三430001596.251620024112.5方案四440001596.252120032112.5

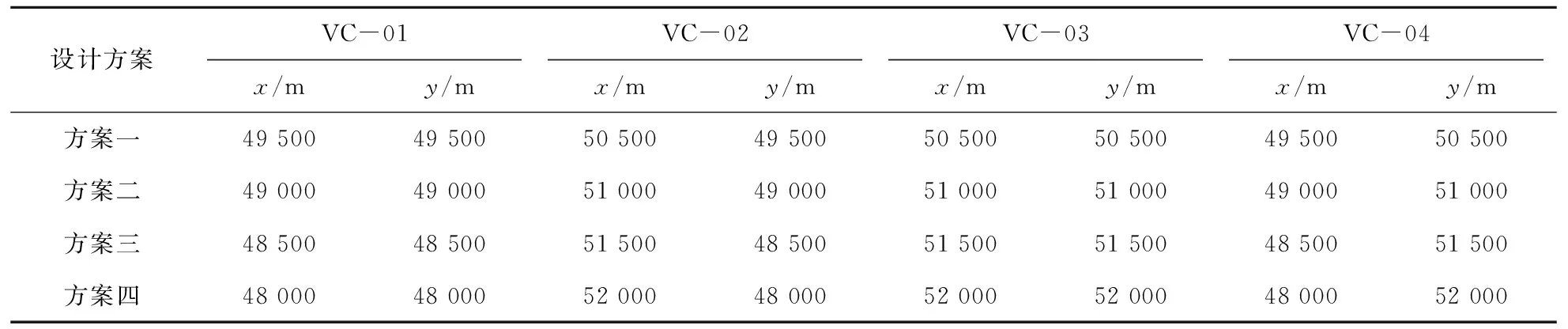
表4 “2阶方阵”接收观测系统设计方案中的VC坐标

注：VC-01、VC-02、VC-03、VC-04分别代表4条不同VC的编号。

图14为4种设计方案的面元覆盖次数，可以看出，当激发面积等于接收面积时，观测面积内的面元覆盖次数分布不均匀，4个角点附近的“矩形”区域面元覆盖次数较高，而“十字形”中心区域的面元覆盖次数较低。此外，随着激发面积和接收面积的增大，4个角点区域的面积逐渐增大，中心区域的面积也会随之增大。可见，当激发面积和接收面积相等时，通过同时增大激发面积和接收面积来提高中心区域面元覆盖次数的方法行不通。

下面以接收面积为1 000 m×1 000 m的“2阶方阵”接收观测系统为例，保持接收面积固定不变，通过增大激发面积来观察中心区域内面元覆盖次数的变化情况(图15)。

图15中4幅图的激发面积分别为1 400 m×1 400 m、2 200 m×2 200 m、3 000 m×3 000 m、3 800 m×3 800 m。由图15可见，当激发面积大于接收面积时，接收区域内的面元覆盖次数高于接收区域外的面元覆盖次数，随着激发面积的增加，观测面积逐渐增加，接收区域内的面元覆盖次数逐渐升高。当激发面积增大到3 800 m×3 800 m时，反射点空白带消失殆尽，接收区域内的面元覆盖次数较为均匀。

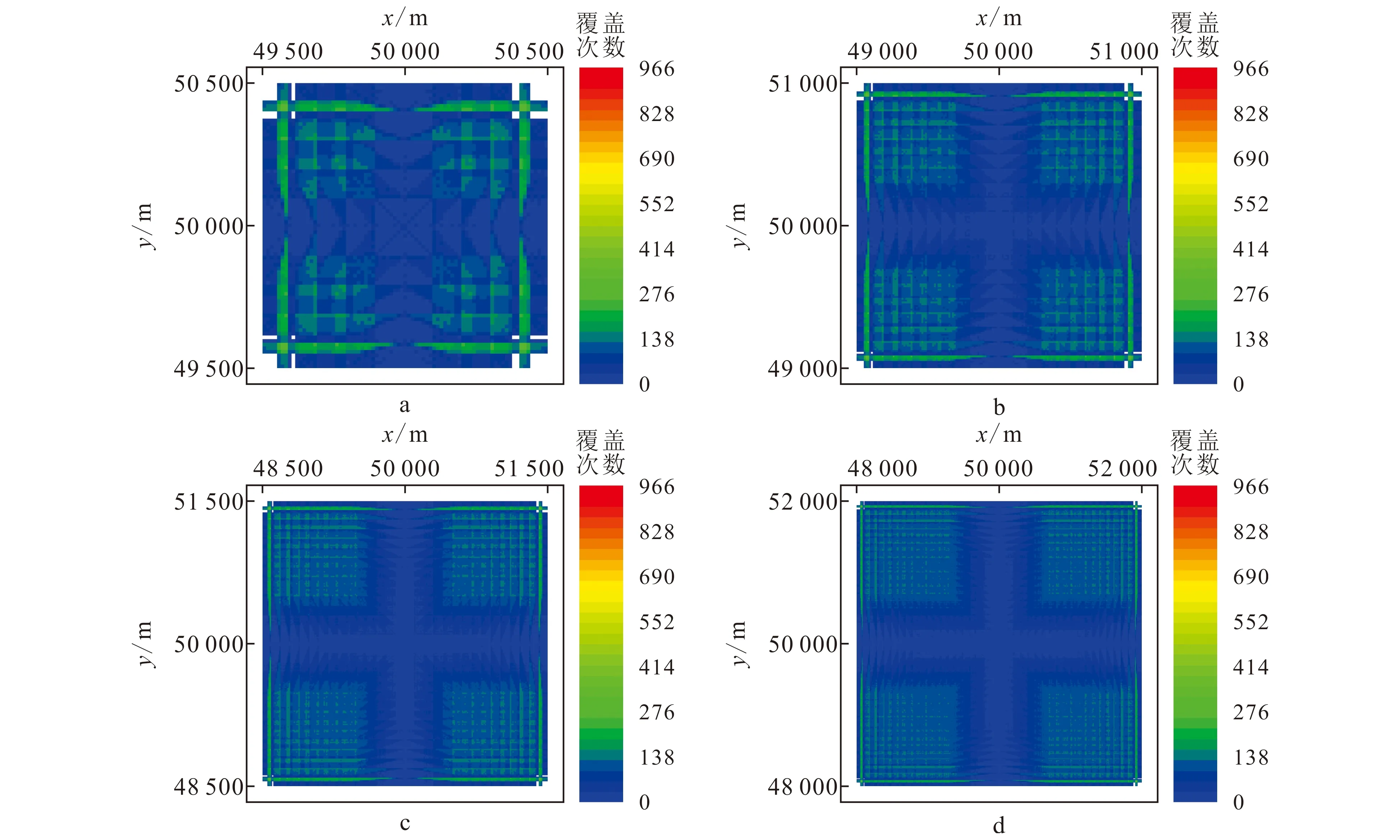
a、b、c、d接收面积依次为1 000 m×1 000 m、2 000 m×2 000 m、3 000 m×3 000 m、4 000 m×4 000 m。图14 “2阶方阵”接收观测系统的面元覆盖次数(激发面积等于接收面积)Fig.14 Bin fold of geometry of two order square matrix when shot area is equal to receiver area

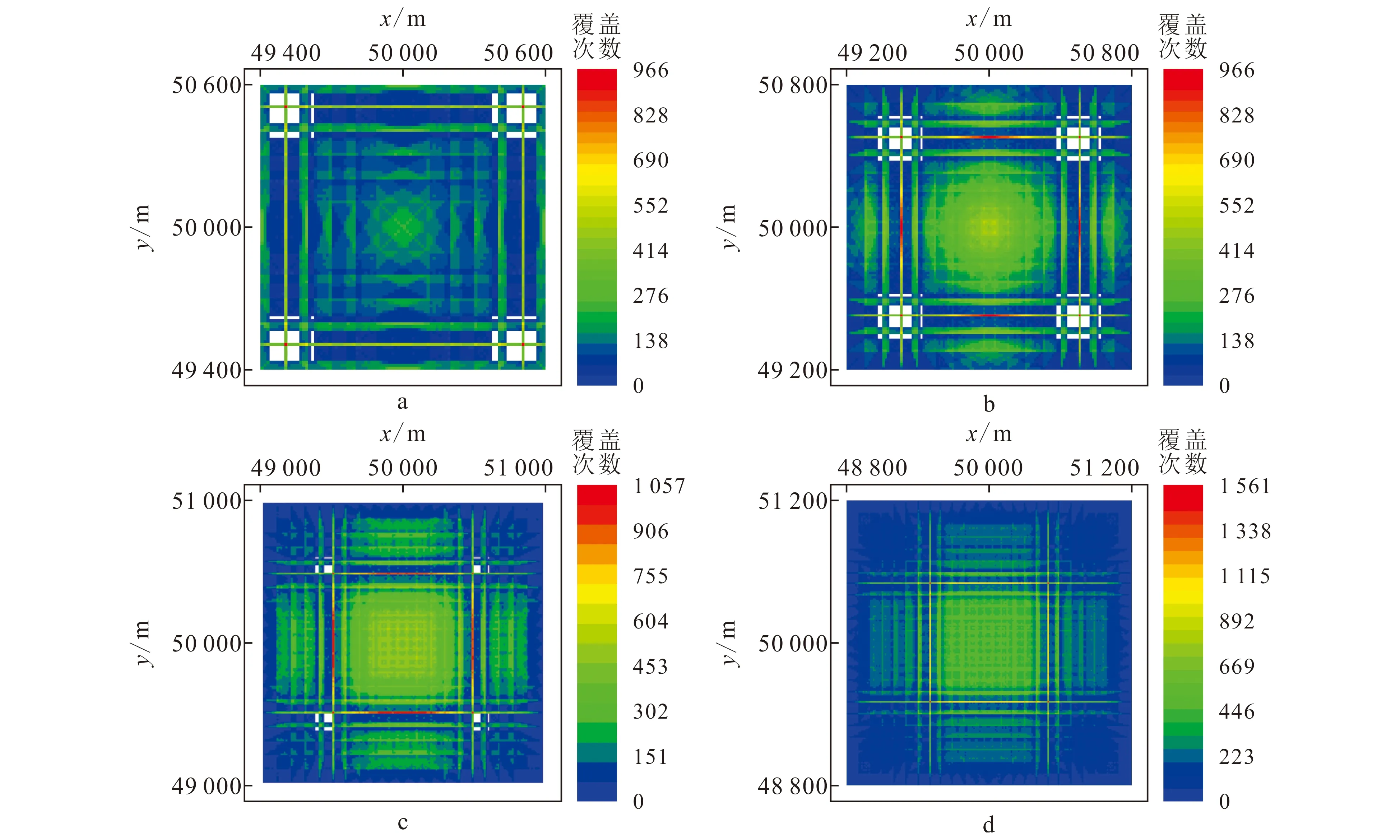
a、b、c、d激发面积依次为1 400 m×1 400 m、2 200 m×2 200 m、3 000 m×3 000 m、3 800 m×3 800 m。图15 “2阶方阵”接收观测系统的面元覆盖次数(激发面积大于接收面积)Fig.15 Bin fold of geometry of two order square matrix when shot area is greater than receiver area

4 结论

1)随着偏移距的增大，同相轴会出现交叉现象，地层顺序也会发生变化。在偏移距增大过程中，有时几个相邻同相轴之间的时差会很小，个别邻近同相轴出现合并现象。因此在设计观测系统时偏移距不宜过大，以上下行波场容易识别为宜。

2)采用增加激发点密度的方法对面元覆盖次数的改善效果要好于采用增加激发面积的方法对面元覆盖次数的改善效果，而且当激发线间距等于激发点间距时，每个面元内的覆盖次数分布均匀性最好。

3)当目标层存在倾角时，目标层照明区域呈梯形，随着倾斜角度的增加，照明强度逐渐向VC位置聚焦。通过在构造走向上增加激发线条数，同时在下倾方向上增加激发线长度可以补偿照明损失。

4)当目标层为背斜或向斜时，通过增大最大环半径来增加背斜和向斜照明范围的方法奏效甚微，即使将VC的位置任意移动也无法对背斜和向斜进行全面观测，这时就需要在以VC坐标为圆心的圆环上布设多条VC以补偿照明损失。

5)当激发面积和接收面积相等时，通过同时增大激发面积和接收面积来提高中心区域面元覆盖次数的方法行不通；而当激发面积大于接收面积时，接收区域内的面元覆盖次数则会高于接收区域外的面元覆盖次数。

[1] 王淑红, 宋海斌, 颜文. 全球与区域天然气水合物中天然气资源量估算[J]. 地球物理学进展, 2005, 20(4): 1145-1154.

Wang Shuhong, Song Haibin, Yan Wen. The Global and Regional Estimation of Gas Resource Quantity in Gas Hydrates[J]. Progress in Geophysics, 2005, 20(4): 1145-1154.

[2] 谈顺佳, 于常青, 聂逢君, 等. 青海南部天然气水合物二维地震探测技术方法试验研究[J]. 地球物理学进展, 2015, 30(2): 817-828.

Tan Shunjia, Yu Changqing, Nie Fengjun, et al. The Experimental Study of 2D Seismic Exploration Technology for Gas Hydrate in the Southern of Qinghai[J]. Progress in Geophysics, 2015, 30(2): 817-828.

[3] 孙嘉鑫, 宁伏龙, 郑明明, 等. 室内沉积物中天然气水合物形成数值模拟研究[J]. 天然气地球科学, 2015, 26(11): 2172-2184.

Sun Jiaxin, Ning Fulong, Zheng Mingming, et al. Numerical Simulation on Natural Gas Hydrate Formation Within Porous Media Using Constant Volume Method[J]. Natural Gas Geoscience, 2015, 26(11): 2172-2184.

[4] 唐志远, 胡云亭, 郭清正, 等. 天然气水合物勘探开发新技术进展[J]. 地球物理学进展, 2015, 30(2): 805-816.

Tang Zhiyuan, Hu Yunting, Guo Qingzheng, et al. Advances in Natural Gas Hydrate Exploration and Development Technology[J]. Progress in Geophysics, 2015, 30(2): 805-816.

[5] 李鹏. 海上全方位观测系统的采集设计方法技术研究[D]. 武汉: 中国地质大学(武汉), 2014.

Li Peng. Study on the Geometries Design of Marine Full-Zimuth Acquisition[D]. Wuhan: China University of Geosciences, 2014.

[6] 吕晓春. 面向目标照明与成像的海上多方位及宽方位观测系统的评价与优化[D]. 武汉: 中国地质大学(武汉), 2014.

Lü Xiaochun. Evaluation and Optimization of Marine Wide-Azimuth and Multi-Azimuth Geometry Acquisition for Target-Oriented Illumination and Imaging[D]. Wuhan: China University of Geosciences, 2014.

[7] Krail P M. Vertical Cable as a Subsalt Imaging Tool[J]. The Leading Edge, 1994, 13(8): 885-887.

[8] Krail P M. Measurements of Cable Shape in a Cross Current[J]. Geophysics, 1994, 59(7): 1156.

[9] Rodriguez-Suarez C, Stewart R R. Survey Design for Vertical Cable Seismic Acquisition[C]//61st EAGE Conference and Exhibition International. Houten: EAGE, 1999.

[10] Moldoveanu N, Henman R, Vlasin J, et al. Bottom Referenced Vertical Hydrophone Arrays-Towed Streamers-a Comparison Study[C]//59th EAGE Conference & Exhibition. Houten: EAGE, 1997: B019.

[11]Ikelle L T. Attenuating Primaries and Free-Surface Multiples of Vertical Cable(VC) Data While Preserving Receiver Ghosts of Primaries[J]. Geophysics, 2001, 66(3): 953-963.

[12] Ikelle L T, Amundsen L, Yoo S. An Optimization of the Inverse Scattering Multiple Attenuation Method for OBS and VC Data[J]. Geophysics, 2002, 67(4): 1293-1303.

[13]Wilson R J. Potential Impacts of Vertical Cable Seismic: Modeling, Resolution and Multiple Attenuation[D]. Texas: Texas A & M University, 2002.

[14] Sun C W, Stratton J, Anderson J, et al. Separation of Up-Going and Down-Going Wave Fields of Vertical Cable Data[J]. Chinese Journal of Oceanology and Limnology, 2005, 23(3): 259-268.

[15] Leach P E. Strathspey Vertical-Cable Seismic Survey: A North-Sea First[C]//Petroleum Geology of Northwest Europe: Proceedings of the 5th Conference. London: Geological Society, 1999: 1235-1242.

[16] Zhang J Z, Huang Y Q, Song L P, et al. Fast and Accurate 3-D Ray Tracing Using Bilinear Traveltime Interpolation and the Wave Front Group Marching[J]. Geophysical Journal International, 2011, 184(3): 1327-1340.

[17]Muerdter D, Ratcliff D. Understanding Subsalt Illumination Through Ray-Trace Modeling, Part 1: Simple 2-D Salt Models[J]. The Leading Edge, 2001, 20(6): 578-594.

[18] Muerdter D, Kelly M, Ratcliff D. Understanding Subsalt Illumination Through Ray-Trace Modeling, Part 2: Dipping Salt Bodies, Salt Peaks, and Nonreciprocity of Subsalt Amplitude Response[J]. The Leading Edge, 2001, 20(7): 688-697.

[19]Muerdter D, Ratcliff D. Understanding Subsalt Illumination Through Ray-Trace Modeling, Part 3: Salt Ridges and Furrows, and the Impact of Acquisition Orientation[J]. The Leading Edge, 2001, 20(8): 803-816.

[20] 杨木壮, 王明君, 吕万军. 南海西北陆坡天然气水合物成矿条件研究[M]. 北京: 气象出版社, 2008.

Yang Muzhuang, Wang Mingjun, Lü Wanjun.The Research of Metallogenic Conditions of Natural Gas Hydrate in the Northwest Slope of the South China Sea [M]. Beijing: Meteorological Press, 2008.

[21] 肖钢, 白玉湖, 董锦. 天然气水合物综论[M]. 北京: 高等教育出版社, 2012.

Xiao Gang, Bai Yuhu, Dong Jin.Review of Natural Gas Hydrate[M]. Beijing: Higher Education Press, 2012.

[22] Kvenvolden K A. Gas Hydrate-Geological Perspective and Global Change[J]. Reviews of Geophysics, 1993, 31(2): 173-187.

[23] Max M D, Lowrie A. Oceanic Methane Hydrates: A “Frontier” Gas Resource[J]. Journal of Petroleum Geology, 1996, 19(1): 41-56.

[24] 邓飞, 刘超颖. 三维射线快速追踪及高斯射线束正演[J]. 石油地球物理勘探, 2009, 44(2): 158-165.

Deng Fei, Liu Chaoying. 3-D Rapid Ray-Tracing and Gaussian Ray-Beam Forward Simulation[J]. Oil Geophysical Prospecting, 2009, 44(2): 158-165.

[25] 宋维琪, 杨晓东. 基于射线追踪的微地震多波场正演模拟[J]. 地球物理学进展, 2012, 27(4): 1501-1508.

Song Weiqi, Yang Xiaodong. The Multi-Wave Field Forward Simulation of Micro-Seismic Based on Ray Tracing[J]. Progress in Geophysics, 2012, 27(4): 1501-1508.

[26] 郭宏伟, 王尚旭, 孙文博. 基于非均质体的波动方程有限元正演模拟[J]. 石油物探, 2012, 51(4): 319-326.

Guo Hongwei, Wang Shangxu, Sun Wenbo.Wave Equation Modeling by Finite-Element Method for Heterogeneous Body[J]. Geophysical Prospecting for Petroleum, 2012, 51(4): 319-326.

[27] 李庆洋, 李振春, 黄建平, 等. 基于贴体全交错网格的起伏地表正演模拟影响因素[J]. 吉林大学学报(地球科学版), 2016, 46(3): 920-929.

Li Qingyang, Li Zhenchun, Huang Jianping, et al.Factor Analysis of Seismic Modeling with Topography Based on a Fully Staggered Body-Fitted Grids[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(3): 920-929.