化学非平衡流动解耦算法的回顾与新进展

刘君S，董海波，刘瑜

1.大连理工大学 航空航天学院，大连 116024 2.航天工程大学 航天装备系，北京 101416

化学非平衡流动与量热完全气体相比，控制方程多出了化学反应源项和组元质量守恒方程组。由于化学反应速率对温度、密度等热力学状态函数极其敏感，导致不同基元反应和同一基元反应的正逆向反应之间的特征时间尺度相差较大，计算过程中存在刚性问题。在20世纪70年代左右，为解决航天器再入过程的热障和黑障问题，需要模拟空气介质的化学非平衡流动，为此提出了点隐算法和全隐算法(统称隐式算法)，目前依然是处理刚性问题的主要算法。现代精细化学研究得到的反应机理越来越复杂，对于碳氢燃料，常包含成百上千种组元和基元反应。复杂反应机理引入的组元方程数目远大于三维量热完全气体流动方程的5个求解变量，例如对于生物柴油燃烧过程，文献[1]给出了1 034种组元、4 236个基元反应的机理模型，采用现有计算方法准确模拟这种化学非平衡流动，控制方程至少需要1 038个偏微分方程构成方程组。采用隐式算法求解刚性问题涉及到矩阵求逆，由此带来的巨大计算量限制了模拟手段在实际三维工程问题中的应用。

为减少求解变量，国内外提出很多算法。早期采用忽略链式反应中间过程的总包反应，例如，1997年梁剑寒和王承尧[2]采用文献[3]提出的两步总包反应模拟超燃冲压发动机内部的氢氧燃烧过程。随着质谱仪等测试手段的进步，对碳氢燃料反应机理研究逐步深入，在此基础上提出反应机理较为简明的替代反应模型，例如针对煤油，黄生洪等[4]对国外提出的两套C12H23替代模型进行考核，修正为17种组元、30个基元反应；杨顺华等[5]根据天津大学测量结果提出10种组元、12个基元反应的n-C10H22替代模型。不同替代反应模型对燃烧最终产物影响较小，但是低温段存在明显差异，对于煤油燃烧这样复杂的化学反应，寻找高低温段特性接近的替代反应模型非常困难。目前，超燃冲压发动机的点火延迟过程和内燃机减少NOx排放的低温燃烧技术作为化学非平衡流动模拟的主要研究背景，新的发展趋势是基于原始复杂模型采用系统辨识、优化算法等数学方法，在保持燃烧过程主要特征的条件下尽可能合并基元反应从而减少组元数目，这一方法称之为骨架反应机理[1]。对上述生物柴油，文献[1]研究结论是可以简化到49种组元、163个基元反应，即使这样采用点隐算法或全隐算法的计算量仍然巨大，为此，近些年部分研究者开始重新审视解耦算法。

解耦算法又称为时间分裂法、分数步法[6]。解耦算法将复杂的多物理问题按照物理意义分解为若干个子问题，然后分别对子问题进行求解。分解后的子问题具有各自的物理特性，针对子问题的计算，通常可以采用相应的成熟算法进行求解，这样相对于完全耦合算法而言，便可以减少问题求解的难度；另外，复杂问题往往存在跨度很大的时间或空间尺度，通过解耦算法分解得到的问题包含相同的物理尺度，因而对于物理尺度的处理会更加灵活，从而可以减少计算时间。由于解耦算法具有以上优点，其应用范围十分广泛，比如生物学[7-8]、金融学[9]、物理学[10-11]等众多领域都有涉及。由于化学反应流动是燃烧过程和流动过程相互耦合的复杂物理现象，是典型的非线性多尺度问题，采用解耦算法对化学非平衡流动进行模拟是一个重要的研究手段。解耦算法应用于化学非平衡流动的模拟，即通过在空间点上把控制方程分解为流动和化学反应两部分，各自采用适合的算法。实际上最早的化学非平衡流动模拟就是采用解耦算法[12]，源项计算采用显式格式，需要上千计算步才能与流动时间推进步长相匹配，由于计算效率低下且不稳定而逐渐被淘汰。虽然采用解耦算法可以大大降低化学反应流动数值模拟的难度，但是由于热物性参数显著依赖于温度的变化，因而在流动计算中，需要大量的工作才能将已有算法移植到化学非平衡流模拟中，而且此过程往往较为繁琐，特别是对于复杂的高阶精度格式更是如此。为了解决这一问题，刘君在其博士论文中提出了一种新颖的非平衡流动解耦算法[13]，通过对能量方程进行分解，将适用于量热完全气体的流动计算格式直接推广到化学非平衡流动的模拟，提高算法改进的效率。随后这种解耦算法不断完善[14-22]，在化学反应求解算法上，从最初采用稳定性较差的梯形算法[19]，替换为稳定性较好的刚性常微分变系数方法(VODE)和拟稳态逼近方法(α-QSS)求解器[20]；汪洪波等[23]将这种解耦算法推广到双时间步法；针对不同网格结构，首先在结构网格上实现了解耦算法[13-14,24]，随后为了适用于复杂计算域，又推广到非结构网格[20-21]，空间离散的精度从2阶推广到了5阶[22]。该解耦算法也被应用于爆轰波模拟[25-27]、固体火箭发动机尾喷流动模拟[24]、横向喷流模拟[28-29]、冲压发动机流场数值模拟[18,24]、旋转爆震波的模拟[30]和弹箭底排装置尾部化学非平衡流模拟[31]等。经过20多年的理论研究和实践应用，验证该解耦算法是成功的，为了区别于传统的化学非平衡流动解耦算法，本文将其命名为“刘君化学非平衡流动解耦算法”，简称为“刘君算法”。

在非平衡流的数值模拟中化学反应的求解工作量巨大，采用常规的求解器，化学反应常微分方程组的计算量为O(N2)～O(N3),其中N为反应组元数目。对于包含上千组元的详细反应机理，化学反应的计算占据整个计算量的绝大部分。为此需要发展高效的化学反应模拟方法。Ren等[41]通过动态自适应化学方法，在每一计算步得到详细的骨架机理，在整个计算精度未受影响的情况下，计算效率提高了3～5倍。Gou等[47]提出了动态多时间尺度(Multi-TimeScale, MTS)方法和混合多时间尺度(Hybrid Multi-TimeScale, HMTS)方法来提高化学反应的计算效率，Sun等[48]将Gou等的动态多时间尺度方法与动态自适应化学方法结合起来形成HMTS/CO-DAC(Hybrid Multi-TimeScale/COrrelated Dynamic Adaptive Chemistry)方法，显著提高了计算效率。值得关注的是目前出现了一种非解耦算法，自适应混合积分(Adaptive Hybrid Integration, AHI)方法[49]及其最新改进型算法(AHI-S)[50]。这种算法在每一步识别出快反应组元和慢反应组元，对于快反应组元采用隐式方法求解，对于慢反应组元采用显式方法求解。这种方法可将化学反应求解的计算量降低到O(N)量级。

1 刘君解耦算法

1.1 出发方程

包含有n种组元的非平衡流守恒型Euler方程为

(1)

式中：F、G和H分别为对流通量在x、y和z方向的分量，具体表达形式参见文献[51]，这里仅给出后面推导用到的守恒变量和源项表达式，即

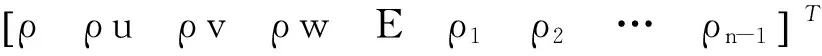
(2)

(3)

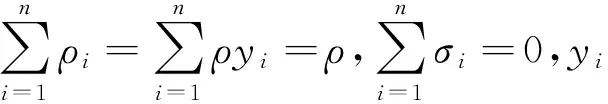
E=0.5ρ(u2+v2+w2)+

(4)

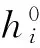
第i个组元定压比热采用的拟合公式为

cpi=Ri(ai+biT+ciT2+diT3+eiT4)

(5)

式中：Ri为组元的气体常数；系数ai、bi、ci、di、ei为常数，具体取值参见文献[52]。

热焓的表达式为

(6)

(7)

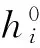
(8)

然后用E′代替E,并且对式(1)进行修改得到新的守恒变量和化学反应源项表达式为

U0=[ρρuρvρwE′ρ1ρ2…ρn-1]T

(9)

(10)

为了说明方程重构所表达的物理意义，进一步引入符号γ′,把E′整理为

(11)

(12)

式中：等效比热比γ′为温度的函数，计算过程中采用二分法迭代得到。

从表达形式上看，E′与量热完全气体的总内能完全相同，称为等效内能；γ′与量热完全气体的比热比相同，称为等效比热比。E′和γ′不符合气体动力学中化学反应混合气体的内能和比热比定义，仅看作物理意义不明确的中间变量。

所有解耦算法在计算源项时隐含假设气体微团总密度和速度保持不变，即

(13)

(14)

代入源项方程E′后得到

(15)

引入等效内能E′和等效比热比γ′以后，将守恒变量U0进一步分解为

U1=[ρρuρvρwE′]T

(16)

U2=[ρ1ρ2…ρn-1]T

(17)

采用时间分裂法把式(1)分解为

(18)

(19)

(20)

U3=[E′ρ1ρ2…ρn-1]T

(21)

(22)

式(18)～式(20)构成刘君算法的出发方程，它和传统解耦算法的差异主要有两点：① 源项方程组包括等效内能E′;② 流动方程的原始守恒变量分解为U0=[U1U2]。

值得说明的是，2003年Deiterding[32]也采用等效内能E′构造了解耦算法，但论文没有给出明确的物理解释，同时没有下面的二次解耦过程。

1.2 算法实现

点隐算法计算量随求解变量非线性增加是由源项线化矩阵D=∂S/∂U∈R(n+4)×(n+4)引起的。全隐算法除D矩阵外，至少还涉及到对流项的系数矩阵，以式(1)中x方向为例，对流项通量的系数矩阵和维数为A=∂F/∂U∈R(n+4)×(n+4)。因此计算量比点隐算法更大。全隐算法随组元变化不但需要改变D和A的维数，其表达形式也需要重新推导。2000年国外学者Choi等[53-54]比较特定算例以后得出的结论表明点隐算法的计算量与方程数目呈2次方规律增加，全隐算法为3次方或更高。

线化矩阵在解耦算法中不是必须的，采用刚性常微分方程计算程序CHEMEQ、LSODE求解化学反应方程组时无需计算Jacobian矩阵，但在构造流动方程计算格式的过程中大多会用到系数矩阵。用于超声速流动的计算格式为了体现扰动沿特征线传播特性，在构造通量分裂格式时需要系数矩阵的特征值。传统解耦算法没有二次解耦，组元变化后需要重新推导表达形式并修改计算程序。

以上算法的控制方程与反应机理相关，不利于解耦算法的工程化应用。守恒变量U1∈R5对应的方程形式与量热完全气体完全相同，无论显式格式或隐式格式离散以后得到的能够体现格式精度和特点的右端项与反应机理无关，编程时仅需将量热完全气体的比热比从常数修改为等效比热比变量，直接采用原来的各种算法。根据解耦算法的机理分析，计算流动方程时流体微团内部组元变换规律和总密度一样，因此，守恒变量U2中各组元的通量分裂格式均采用U1中密度ρ的表达式，这样形成的右端项与组元数目相关，但是计算表达式是统一的，不需重新推导公式和修改程序，易于实现软件工程化。

用于隐格式求解时，守恒变量U1系数矩阵A1=∂F1/∂U1∈R5×5与量热完全气体完全相同，守恒变量U2系数矩阵A2=∂F2/∂U2∈R(n-1)(n-1)为对角矩阵。如果U1和U2耦合计算，总变量U0的系数矩阵由A1和A2按照块对角构成，形式简单，组元数目增减也不需要重新编程。U1和U2也可以不耦合，在后面新进展中介绍。

按照以上解耦算法建立流体和反应求解模块，化学反应方程的求解涉及到刚性问题，因此反应源项方程表示为Ls,而流动算子为Lf，为保证时间二阶精度，总算子采用的形式为

(23)

传统解耦算法在源项方程时间推进以后仅改变组元，反应过程引起的压力等流场参数变化需要等到流动方程求解以后才能体现，式(3)中源项的第5项对应为能量项，其值为0，说明在进行化学反应计算中压力等流场参数未更新，只改变了组元的质量分数。相对于传统解耦算法，刘君算法同样保持气体微团总内能E不变，式(10)中源项的第5项对应为能量项，其表达形式涉及到压力、温度等物性参数的求解，通过对源项方程的计算既改变组元的质量分数，同时也计算了化学能转化为压力能的热力学过程。采用图1可以说明两种算法的差异，图中使用不同形状代表流体微团的状态参数，Ci表示不同状态下组元的质量分数矩阵。图1(a)代表传统解耦算法，流体微团通过反应算子Ls计算源项方程得到不同组元以后，改变了流体微团内部的质量分数，而压力、总密度未发生改变，然后通过流动算子Lf的求解确定流体微团热力学状态参数；从图1(b)中可以清晰地看出刘君算法的物理意义，通过反应源项算子Ls求解源项方程，此过程模拟了流体微团在当地绝热(E不变)、定容(ρ不变)的热力学系统内发生的化学反应过程，状态参数和组元变化耦合求解，通过Lf求解流动方程，模拟组元质量分数yi保持不变的流体微团沿流线运动(冻结流)，包括密度在内的状态参数随位置变化。

图1 传统解耦算法和刘君算法的原理差异Fig.1 Difference between classical uncoupled algorithm and modified algorithm

2 发展历程

刘君[13]于1993年在其博士学位论文中提出了一种解耦算法，其研究团队20多年来不断对算法进行改进，在介绍最新进展前先简要回顾发展历史。

2.1 有限差分法

最早的刘君算法采用时空二阶的NND2M(Nonoscillatory Nonfree Dissipative second order Modified)单步差分格式求解流动偏微分方程组，对流项通量采用VanLeer格式，反应常微分方程组采用梯形公式求解，由于源项计算耗时很少，总算子采用式(23)。通过模拟弹道靶试验[55]来检验算法的精度，计算发现弹丸飞行速度大于气体爆轰速度时“超爆轰”模态效果很好，驻点线上Von Neumann Spike现象的位置和峰值与国内外文献结果完全一致，表明解耦算法的空间精度达到预期，但是针对弹丸飞行速度接近爆轰速度的“跨爆轰”模态始终没有模拟出振荡现象，当时怀疑算法时间精度不满足要求，一直未在学术期刊发表。直到2000年看到文献[53-54]才发现网格尺度和反应机理的重要性，最终模拟出燃烧阵面进行周期性振荡的稳定燃烧流场[15]，进一步分别对氢气和空气燃烧的3种反应动力学模型进行比较研究[17]，得出的结论认为组元HO2和H2O2及其相关基元反应是模拟振荡燃烧的关键因素，采用复杂反应机理能够准确模拟混合气体的点火延迟特性。在此基础上模拟了高速弹丸在氢气/空气预混气体、甲烷/空气预混气体中形成的流场[18]，通过对比不同反应动力学模型的计算耗时后得到的结论认为刘君解耦算法的计算量与求解变量呈线性规律变化。为了考察计算效率，采用40万网格和19种组元、66个基元反应的甲烷/空气燃烧模型，在主频为1 GHz、内存为128 MB的Winbook6630笔记本电脑上完成了超燃冲压加速器三维流场模拟。其后，采用该算法针对固体火箭发动机装药裂纹、超声速飞行器喷流控制系统和液体火箭发动机火箭底部阻力等包含有非平衡流动的实际工程问题开展研究并取得实效[56-59]。

通过对工程应用的经验总结，发现采用梯形公式求解存在刚性问题的非线性常微分方程组是造成收敛鲁棒性较差等问题的主要原因。经过对算法进行改进，采用VODE和α-QSS两种求解器替换梯形公式解决了上述问题[60]，但是计算效率明显降低，尤其是在总算子采用式(23)模拟“超爆轰”模态时，Ls算子的CPU时间超过Lf算子。在其他计算条件相同的情况下，流场稳定以后比较每个时间步内Ls所占CPU时间比例，采用1/10流动时间步长的梯形公式为8%、VODE为84%、α-QSS为53%[24]。

2.2 有限体积法

对式(1)进行空间积分，通过高斯公式把体积分变化为面积分，得到有限体积法的出发方程为

(24)

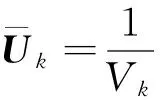
化学反应过程采用Arrhenius模型，源项S表示为组元密度、温度的指数型函数。空间一阶精度有限体积法假设物理量在控制体内为常数，源项的体积分可以直接得到,其表达式为

(25)

(26)

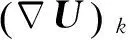
时间分裂法早期被用来解决模拟复杂工程问题时所遇到的计算机内存不足难题，其理论基础是在空间点上采用时间方向迭代降低空间算子维数，以增加CPU时间为代价减少内存开销。采用解耦算法在空间点上进行时间分裂法的同时可以解决有限体积法的源项精度问题。时间分裂以后流动偏微分方程不包含化学反应源项，因此不需要计算源项函数的体积分；源项函数只在化学反应的常微分方程中出现，与空间离散无关；如果偏微分方程和常微分方程均采用时间二阶精度算法，决定整个化学非平衡流动计算空间精度的是流动方程的空间离散精度。基于解耦算法的有限体积法理论上具有时空二阶精度。实际上利用有限体积法空间平均特性还可以建立不需要求解U2方程组的优化算法。

3 研究新进展

通过对国内外研究现状调研，认为提高计算效率是解决化学非平衡流动模拟在实际工程应用中发挥效益的关键，近期对解耦算法理论和工程应用进行系统整理后发现，计算效率还有改进空间，提出如下优化算法和处理技术。

3.1 流动方程优化算法

结合刘君解耦算法机理和有限体积法空间平均特性，提出如图2所示的优化算法：假设在Δt时间步内，流体微团从控制体单元k流出到单元3，从相邻单元1和2流入。由于U1和U2方程解耦，可以单独计算U1的方程，记录进出边界的质量流量，例如，单元1外法向速度为un,流量为m1=(ρunSΔt)1,其中S为面元面积，流场从tn时刻推进到tn+1时刻。优化解耦算法的流动方程本质是模拟冻结流，随流体微团进出控制体过程中没有发生化学反应，组元质量分数yi保持不变，根据质量守恒，Δt时间内控制体组元i的密度平均值为

(27)

优化算法的优势在于方程求解过程中不需要计算U2的偏微分方程组就可以得到U2。

图2 优化算法机理示意图Fig.2 Schematic of optimization algorithm mechanism

3.2 验证算例

采用250×200的计算网格、修正的Jachimowski(9种组元、19个基元反应)化学反应机理模拟经典的激波诱导燃烧试验，试验来流条件压力p∞为42 650 Pa，温度T∞为293 K。模拟弹丸飞行马赫数Ma=6.46的超爆轰模态得到的密度云图中激波阵面和燃烧阵面位置与试验比较如图3所示，试验采用的弹丸半径R为7.5 mm，图中显示的横纵坐标均为无量纲坐标。化学反应的诱导时间主要取决于流场中的温度，即温度越高化学反应诱导时间越短。混合气体经过弹丸头部附近正激波后，由于激波强度大、温度高，导致此区域附近诱导时间最短。而诱导区厚度是由诱导时间决定的，在驻点流线上激波阵面与燃烧阵面几乎重合在一起，垂直于弓形激波的速度分量等于爆轰速度，文献[63]也对此现象有详细的解释。通过对比发现数值模拟结果与试验结果是一致的。远离驻点流线，激波强度和流场温度开始降低，所以诱导时间增加，导致激波阵面与燃烧阵面逐渐分离。在出口附近，模拟结果与试验结果之间存在一定的误差，主要原因是Jachimowski反应机理中放热效果更加显著，斜激波强度高于试验值，使得模拟结果中阵面的位置均高于试验结果。

图3 计算结果与试验结果对比Fig.3 Comparison between calculated and test results

沿驻点线压力、温度分布和文献[24]的比较结果如图4所示。ZND(Zeldovich Neumann Doering)爆轰理论[64]认为：前导激波将可燃气体压缩加热到其自燃状态，经过诱导区后开始发生化学反应并迅速释放化学能，诱导反应区后温度、压强、密度等状态量急剧变化，借助化学反应释放的能量使燃烧气体膨胀并支撑前导激波以一定马赫数传播。类似于传统的燃烧现象，化学反应区是一个温度升高、压力基本持平的过程，燃烧气体的热力学参数在放热区的末端达到CJ(Chapman Jouget)爆轰状态。ZND模型考虑了爆轰燃烧的非平衡过程，并提出了能够解释爆轰波自持传播的化学反应过程与前导激波相互作用的机制。本文采用的基元化学反应模型中，化学反应速率遵循Arrhenius规律，符合ZND模型的基本假设，从模拟结果中显示出Von Neumann Spike现象，压力峰值是由于波后的剧烈燃烧和能量释放，难以维持等压燃烧造成的。显然，如果能量释放率越高，那么Von Neumann Spike现象将更加明显。从计算结果可以看出本文使用的方法很好地模拟出Von Neumann Spike现象，与文献[24]的结果也基本一致，说明优化算法具有很好的精度。

图5所示为优化算法与刘君算法得到的密度云图对比。 图5分为上下两部分，分别采用两种方法的收敛解进行结果对比分析。以上模拟结果验证了优化算法对于定常流场具有较好的空间分辨率。

图4 沿驻点线压力、温度分布的计算结果与文献[24]试验结果的比较Fig.4 Comparison of pressure and temperature distribution obtained by calculation with test results of Ref.[24] along stagnation line

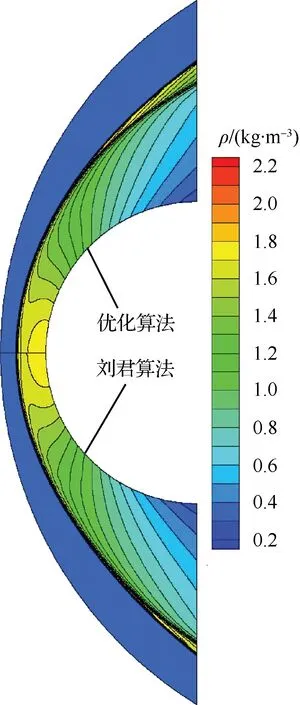
图5 超爆轰密度云图Fig.5 Density contours of super detonation

图6 驻点线上密度等值线的时间历程(Ma=4.79)Fig.6 History of density contours on stagnation line (Ma=4.79)

为了验证优化算法的准确性，对Lehr试验[55]中激波诱导周期性振荡燃烧算例进行数值模拟。与试验来流条件相同，采用H2/Air混合气体在压力p∞为42 650 Pa、温度T∞为293 K的条件下进行计算，弹丸的飞行马赫数分别为Ma=4.79和Ma=4.48。为得到较好的计算结果，使用350×300的计算网格，采用文献[62]提出的通量格式和限制器函数分别对两种条件下跨爆轰算例进行模拟，图6和图7分别为采用优化算法模拟跨爆轰模态得到的驻点线上密度的时间历程等值线。模拟结果显示出明显的周期性振荡燃烧现象并且在表1中列出了与其他结果[53,55]的数据对比。本文的模拟结果与其他数据误差很小，验证了本文模拟结果的准确性。

图7 驻点线上密度等值线的时间历程(Ma=4.48)Fig.7 History of density contours on stagnation line (Ma=4.48)

表1 振荡频率对比Table 1 Comparison of oscillation frequency

数据来源频率/kHzMa=4.79Ma=4.48Lehr试验[55]712425文献[53]707426本文结果706422

3.3 耦合过程的空间优化

优化算法求解过程中不计算U2,计算效率仅提高14.6%，主要原因是采用VODE和α-QSS求解器在改善常微分方程组求解稳定性的同时增加了计算源项的CPU时间。注意到在很多工程问题中化学反应仅发生在流场局部区域，在未反应或反应达到平衡的空间区域组元质量生成率σi≈0,没有必要计算源项。在t0时刻整个预混燃气的流场温度保持相同，采用流动算子Lf对流场参数进行更新以后，激波后区域的温度会逐渐上升，温度越高化学反应进行得越剧烈，计算得到的组元生成率越大。由于激波前区域仍保持为初始来流参数，不需要进行化学反应计算，而激波后区域温度上升，化学反应更加剧烈，因此可以把初始时刻进行的化学反应作为基准来对全场区域进行标识。基于以上认识，利用解耦算法的特点，在t0时刻采用反应算子Ls对所有单元进行一次化学反应计算，同时记录下所有单元中组元生成率绝对值的最大值为

(28)

以式(28)为判据准则在随后的计算中对所有控制体单元的质量生成率进行判断，当满足判断条件

(29)

将控制体及其相邻控制体进行标识，整理流场完成分类后仅在标识过的控制体内调用Ls算子。

针对马赫数Ma=6.46的超爆轰模态，通过t0时刻计算得到的准则参数ε1=2.66×10-13kg/s进行辨识，CPU时间随计算步数变化曲线如图8所示，通过标识得到的化学反应计算区域如图9中阴影部分所示，大约占总体计算区域的2/3左右，图9(a)中对局部计算网格区域进行放大处理，图中加粗黑线为进行质量生成率判别后进行标记的反应区分界面。表2列出不同计算步数时CPU时间对比，通过采用质量生成率判据，化学反应算子计算效率明显提高，总CPU时间也随之降低。空间优化算法同样适用于跨爆轰模态，图9(b)流场中两条曲线分别代表两个时刻的化学反应区域，由于化学反应区域随时间发生变化，没有比较计算效率。

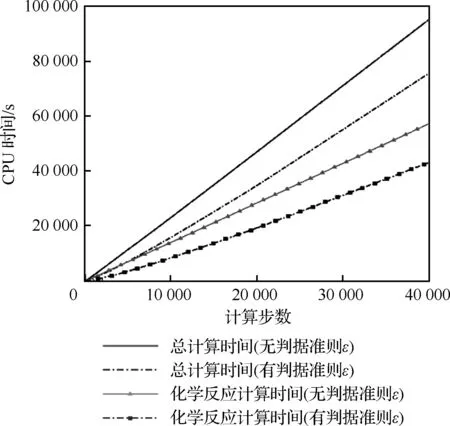
图8 CPU时间随计算步数的变化曲线Fig.8 Variation curves of CPU time with calculated steps

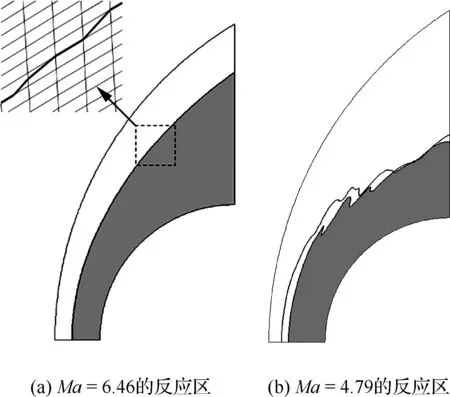
图9 添加判据后进行化学反应区域示意图Fig.9 Schematic of chemical reaction region after addition of criterion

表2 总CPU时间对比Table 2 Comparison of total CPU time

计算步数总CPU时间/s无判据准则ε有判据准则ε1000023222.515121.22000047096.932968.14000095130.471515.6

4 结束语

在回顾1993年刘君提出的化学非平衡流动解耦算法及其发展历史之后，采用有限体积法空间平均特性对刘君解耦算法进行了改进并提出耦合过程中的空间优化算子，模拟结果显示优化算法可以显著提高化学非平衡流模拟的计算效率。在此基础上，今后研究的重点将转向集成国外新成果来提高化学反应算子的计算效率。

[1] 常亚超. 基于解耦法的柴油和生物柴油表征燃料骨架反应机理研究[D]. 大连： 大连理工大学, 2016: 1-13.

CHANG Y C. Investigation of skeletal chemical mechanisms for diesel and biodiesel surrogate fuel based on decoupling methodology[D]. Dalian: Dalian University of Technology, 2016: 1-13 (in Chinese).

[2] 梁剑寒, 王承尧. 超燃冲压发动机燃烧室三维化学反应流场的数值模拟[J]. 推进技术, 1997, 18(4): 1-4.

LIANG J H, WANG C Y. 3D numerical simulation of supersonic reacting flows in scramjet combustion[J]. Journal of Propulsion Technology, 1997, 18(4): 1-4 (in Chinese).

[3] ROGERS R C, CHINITZ W. Using a global hydrogen-air combustion model in turbulent reacting flow calculations[J]. AIAA Journal, 1983, 21(4): 586-592.

[4] 黄生洪, 徐胜利, 刘小勇. 煤油超燃冲压发动机两相流场数值模拟(I)数值校验及总体流场特征[J].推进技术, 2004, 25(6): 484-490.

HUANG S H, XU S L, LIU X Y. Numerical investigation on two phase flow of akerosene-fueled scramjet with 3D cavity (I) Numerical calibration and characteristics of general flow[J]. Journal of Propulsion Technology, 2004, 25(6): 484-490 (in Chinese).

[5] 杨顺华， 乐嘉陵， 赵慧勇， 等. 煤油超燃冲压发动机三维大规模并行数值模拟[J]. 计算物理， 2009， 26(4)： 534-540.

YANG S H, LE J L, ZHAO H Y, et al. Three-dimensional massively parallel numerical simulation of kerosene-fueled scramjet[J]. Chinese Journal of Computational Physics, 2009, 26(4): 534-540 (in Chinese).

[6] YANENKO N N. The method of fractional steps[M]. Heidelberg: Springer-verlag, 1971: 42-50.

[7] DESCOMBES S, DUMONT T. Numerical simulation of a stroke: Computational problems and methodology[J]. Progress in Biophysics & Molecular Biology, 2008, 97(1): 40-53.

[8] DUMONT T, DUARTE M, DESCOMBES S, et al. Simulation of human ischemic stroke in realistic 3D geometry[J]. Communications in Nonlinear Science & Numerical Simulation, 2013, 18(6): 1539-1557.

[9] CUI S, KURGANOV A, MEDOVIKOV A. Particle methods for PDEs arising in financial modeling[J]. Applied Numerical Mathematics, 2015, 93: 123-139.

[10] DESCOMBES S, THALHAMMER M. The Lie-Trotter splitting for nonlinear evolutionary problems with critical parameters: A compact local error representation and application to nonlinear schrödinger equations in the semiclassical regime[J]. IMA Journal of Numerical Analysis, 2013, 33(2): 722-745.

[11] KULIKOV I, VOROBYOV E. Using the PPML approach for constructing a low-dissipation, operator-splitting scheme for numerical simulations of hydrodynamic flows[J]. Journal of Computational Physics, 2016, 317: 318-346.

[12] CAMBIER J, ADELMAN H, MENEES G P. Numerical simulations of an oblique detonation wave engine[J]. Journal of Propulsion and Power, 1990, 6(3): 315-323.

[13] 刘君. 超音速完全气体和H2/O2燃烧非平衡气体的复杂喷流流场数值模拟[D]. 绵阳： 中国空气动力研究与发展中心, 1993: 56-65.

LIU J. Numerical simulation of the complex jet flow field of supersonic gas and H2/O2combustion[D]. Mianyang: China Aerodynamics Research and Development Center, 1993: 56-65 (in Chinese).

[14] 刘君, 张涵信, 高树椿. 一种新型的计算化学非平衡流动的解耦方法[J]. 国防科技大学学报, 2000, 22(5): 19-22.

LIU J, ZHANG H X, GAO S C. A new uncoupled method for numerical simulation of non-equilibrium flow[J]. Journal of National University of Defense Technology, 2000, 22(5): 19-22 (in Chinese).

[15] 刘君. 冲压加速器非平衡流动数值模拟[J]. 弹道学报, 2002, 14(4): 31-35.

LIU J. Numerical study on the non-equilibrium flow of ram accelerator in the combustive mixture gas[J]. Journal of Ballistics, 2002, 14(4): 31-35 (in Chinese).

[16] 刘君. 非平衡流计算方法及其模拟激波诱导振荡燃烧[J]. 空气动力学学报, 2003, 21(1): 53-58.

LIU J. A new non-equilibrium numerical method and simulation of oscillating shock-induced combustion[J]. Acta Aerodynamica Sinica, 2003, 21(1): 53-58 (in Chinese).

[17] 刘君. 化学动力学模型对H2/Air超燃模拟的影响[J]. 推进技术, 2003, 24(1): 67-70.

LIU J. Numerical study on chemical mechanism in supersonic H2/Air mixture gas flow[J]. Journal of Propulsion Technology, 2003, 24(1): 67-70 (in Chinese).

[18] 刘君. 甲烷/空气超声速燃烧流动数值模拟[J]. 推进技术, 2003, 24(4): 296-299.

LIU J. Numerical study for CH4/air supersonic combustion[J]. Journal of Propulsion Technology, 2003, 24(4): 296-299 (in Chinese).

[19] 刘君, 刘瑜, 周松柏. 基于新型解耦算法的激波诱导燃烧过程数值模拟[J]. 力学学报, 2010, 42(3): 572-578.

LIU J, LIU Y, ZHOU S B. Simulation of shock induced combustion based on a novel uncoupled method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 572-578 (in Chinese).

[20] 刘瑜. 化学非平衡流的计算方法研究及其在激波诱导燃烧现象模拟中的应用[D].长沙： 国防科学技术大学, 2008: 20-24.

LIU Y. Investigations into numerical methods of chemical nonequilibrium flow and its application to simulation of shock-induced combustion phenomena[D]. Changsha： National University of Defense Technology, 2008: 20-24 (in Chinese).

[21] 刘瑜, 刘君, 白晓征. 基于新型非结构有限体积解耦算法的激波诱导燃烧数值模拟[J]. 国防科技大学学报, 2011, 33(6): 139-144.

LIU Y, LIU J, BAI X Z. Numerical simulation of shock-induced combustion with a new uncoupled algorithm in university finite volume method[J]. Journal of National University of Defense Technology, 2011, 33(6): 139-144 (in Chinese).

[22] 刘瑜, 刘君, 唐玲艳, 等. 一种求解化学非平衡流动的新型解耦算法[J]. 力学学报, 2015, 47(1): 82-94.

LIU Y, LIU J, TANG L Y, et al. A novel uncoupled algorithm for solving chemical nonequilibrium flows[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(1): 82-94 (in Chinese).

[23] 汪洪波, 孙明波, 梁剑寒, 等. 含双时间步法的化学非平衡流解耦算法[J]. 计算物理, 2010, 27(5): 685-691.

WANG H B, SUN M B, LIANG J H, et al. An uncoupled method with dual time-step for chemical nonequilibrium flows[J]. Chinese Journal of Computational Physics, 2010, 27(5): 685-691 (in Chinese).

[24] 周松柏. 超声速内外流干扰的数值方法研究及其实验验证与应用[D]. 长沙： 国防科学技术大学, 2009: 76-92.

ZHOU S B. Research on numerical method, experimental verification and application in simulation jet interaction in supersonic external flow[D]. Changsha： National University of Defense Technology, 2009: 76-92 (in Chinese).

[25] 孙明波, 梁剑寒, 王振国. 非平衡流解耦方法及其计算激波诱导燃烧的应用验证[J]. 航空动力学报, 2008, 23(11): 2055-2061.

SUN M B, LIANG J H, WANG Z G. Validation of an uncoupled solver of non-equilibrium flow for shock-induced combustion[J]. Journal of Aerospace Power, 2008, 23(11): 2055-2061 (in Chinese).

[26] 刘世杰, 孙明波, 林志勇, 等. 钝头体激波诱导振荡燃烧现象的数值模拟[J]. 力学学报, 2010, 42(4): 597-606.

LIU S J, SUN M B, LIN Z Y, et al. Numerical research on blunt body shock-induced oscillating combustion phenomena[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 597-606 (in Chinese).

[27] 韩旭, 周进, 林志勇, 等. 突跃型与平滑型斜爆震波起爆机制数值模拟[J]. 航空动力学报, 2012, 27(12): 2674-2680.

HAN X, ZHOU J, LIN Z Y, et al. Initiation mechanism investigation of saltation and smoothness oblique detonation waves[J]. Journal of Aerospace Power, 2012, 27(12): 2674-2680 (in Chinese).

[28] 刘君, 杨彦广. 带有横喷控制的导弹流场数值模拟[J]. 空气动力学学报, 2004, 22(3): 309-312.

LIU J, YANG Y G. Numerical simulation of lateral jet control of a hypersonic missile[J]. Acta Aerodynamica Sinica, 2004, 22(3): 309-312 (in Chinese).

[29] 杨彦广, 刘君, 唐志共. 横向喷流干扰中的真实气体效应研究[J]. 空气动力学学报, 2006, 24(1): 28-33.

YANG Y G, LIU J, TANG Z G. A study of real gas effects on lateral jet interaction[J]. Acta Aerodynamica Sinica, 2006, 24(1): 28-33 (in Chinese).

[30] 刘世杰, 林志勇, 孙明波, 等. 旋转爆震波发动机二维数值模拟[J]. 推进技术, 2010, 31(5): 634-640.

LIU S J, LIN Z Y, SUN M B, et al. Two-dimensional numerical simulation of rotating detonation wave engine[J]. Journal of Propulsion Technology, 2010, 31(5): 634-640 (in Chinese).

[31] 余文杰, 余永刚. 底排装置尾部化学非平衡流的数值模拟[J]. 推进技术, 2015, 36(11): 1610-1615.

YU W J, YU Y G. Numerical simulation of base flow with chemical non-equilibrium for base bleed equipment[J]. Journal of Propulsion Technology, 2015, 36(11): 1610-1615 (in Chinese).

[32] DEITERDING R. Parallel adaptive simulation of multidimensional detonation structures[D]. Cottbus: Brandenburg University of Technology, 2003: 18-27.

[33] ZIEGLER J L, DEITERDING R, SHEPHERD J E, et al. An adaptive high-order hybrid scheme for compressive, viscous flows with detailed chemistry[J]. Journal of Computational Physics, 2011, 230(20): 7598-7630.

[34] BILLET G, RYAN J. A runge kutta discontinuous Galerkin approach to solve reactive flows: The hyperbolic operator[J]. Journal of Computational Physics, 2011, 230(4): 1064-1083.

[35] BILLET G, RYAN J, BORREL M. A Runge Kutta discontinuous Galerkin approach to solve reactive flows on conforming hybrid grids: The parabolic and source operators[J]. Computers and Fluids, 2014, 95: 98-115.

[36] LV Y, IHME M. Discontinuous Galerkin method for multicomponent chemically reacting flows and combustion[J]. Journal of Computational Physics, 2014, 270: 105-137.

[37] GLOWINSKI R, OSHER S J, YIN W. Splitting methods in communication, imaging, science, and engineering[M]. Heidelberg: Springer-Verlag, 2016: 627-641.

[38] TROTTER H F. On the product of semi-groups of operators[J]. Proceedings of the American Mathematical Society, 1959, 10(4): 545-551.

[39] STRANG G. On the construction and comparison of difference schemes[J]. SIAM Journal on Numerical Analysis, 1968, 5(3): 506-517.

[40] LU P. A consistent-splitting approach to computing stiff steady-state reacting flows with adaptive chemistry[J]. Combustion Theory and Modelling, 2003, 7(2): 383-399.

[41] REN Z, XU C, LU T, et al. Dynamic adaptive chemistry with operator splitting schemes for reactive flow simulations[J]. Journal of Computational Physics, 2014, 263: 19-36.

[42] DUARTE M. Adaptive numerical methods in time and space for the simulation of multi-scale reaction fronts[D]. Paris: Ecole Centrale Paris, 2011: 104-128.

[43] DUARTE M, DESCOMBES S, TENAUD C, et al. Time-space adaptive numerical methods for the simulation of combustion fronts[J]. Combustion and Flame, 2013, 160(6): 1083-1101.

[44] HELLANDER A, LAWSON M J, DRAWERT B, et al. Local error estimates for adaptive simulation of the reaction-diffusion master equation via operator splitting[J]. Journal of Computational Physics, 2014, 266: 89-100.

[45] SPORTISSE B. An analysis of operator splitting techniques in the stiff case[J]. Journal of Computational Physics, 2000, 161(1): 140-168.

[46] SANTILLANA M, ZHANG L, YANTOSCA R. Estimating numerical errors due to operator splitting in global atmospheric chemistry models: Transport and chemistry[J]. Journal of Computational Physics, 2015, 305: 909-917.

[47] GOU X, SUN W, CHEN Z, et al. A dynamic multi-timescale method for combustion modeling with detailed and reduced chemical kinetic mechanisms[J]. Combustion and Flame, 2010, 157(6): 1111-1121.

[48] SUN W, GOU X, ELASRAG H A, et al. Multi-timescale and correlated dynamic adaptive chemistry modeling of ignition and flame propagation using a real jet fuel surrogate model[J]. Combustion and Flame, 2015, 162(4): 1530-1539.

[49] YANG G, LIU Y, REN Z, et al. A dynamic adaptive method for hybrid integration of stiff chemistry[J]. Combustion and Flame, 2015, 162(2): 287-295.

[50] XU C, GAO Y, REN Z, et al. A sparse stiff chemistry solver based on dynamic adaptive integration for efficient combustion simulations[J]. Combustion and Flame, 2016, 172: 183-193.

[51] 刘君, 周松柏, 徐春光. 超声速流动中燃烧现象的数值模拟方法及应用[M]. 长沙：国防科学技术大学出版社, 2008: 61-63.

LIU J, ZHOU S B, XU C G. The numerical simulation method of supersonic flow and its application[M]. Changsha: National University of Defense Technology Press, 2008: 61-63 (in Chinese).

[52] GUPTA R N, YOS J M, THOMPSON R A. A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal non-equilibrium calculations to 30000 K[J]. Philosophy, 1990, 92(6): 32-34.

[53] CHOI J Y, JEUNG I S, YOON Y, et al. Computational fluid dynamics algorithms for unsteady shock-induced combustion, Part 1: Validation[J]. AIAA Journal, 2000, 38(7): 1179-1187.

[54] CHOI J Y, JEUNG I S, YOON Y. Computational fluid dynamics algorithms for unsteady shock-induced combustion, Part 2: Comparison[J]. AIAA Journal, 2000, 38(7): 1188-1195.

[55] LEHR H F. Experiments on shock-induced combustion[J]. Acta Astronautica, 1972(1): 589-597.

[56] 杨彦广, 刘君. 高超声速主流中横向喷流干扰非定常特性研究[J]. 空气动力学学报, 2004, 22(3): 295-302.

YANG Y G, LIU J. Unsteady characteristic research of lateral jet in hypersonic external flow[J]. Acta Aerodynamica Sinica, 2004, 22(3): 295-302 (in Chinese).

[57] 徐春光, 刘君. 某型导弹尾喷流形状的数值模拟[J]. 推进技术, 2003, 24(2): 141-143.

XU C G, LIU J. Numerical simulation on the plume flow structures for a missile[J]. Journal of Propulsion Technology, 2003, 24(2): 141-143 (in Chinese).

[58] 周松柏, 刘君, 郭正, 等. 激波诱导异质气体界面失稳的数值模拟[J]. 国防科技大学学报, 2009, 31(1): 1-4.

ZHOU S B, LIU J, GUO Z, et al. Numerical simulation for shock induced interfacial instabilities of heterogeneous gases[J]. Journal of National University of Defense Technology, 2009, 31(1): 1-4 (in Chinese).

[59] 崔小强, 白晓征, 周伟, 等. 点火冲击波与药柱裂纹流固耦合作用机理数值模拟研究[J]. 固体火箭技术, 2010, 33(1): 9-12.

CUI X Q, BAI X Z, ZHOU W, et al. Numerical simulation of the fluid-structure interaction mechanism between ignition shock wave and elastic cracks of grain[J]. Journal of Solid Rocket Technology, 2010, 33(1): 9-12 (in Chinese).

[60] 刘瑜. 量热完全气体/化学非平衡气体流动ALE有限体积计算方法研究[D]. 长沙： 国防科学技术大学, 2014: 128-134.

LIU Y. Numerical research of ALE finite volume method for calorically perfect gas chemical nonequilibrium gas flow[D]. Changsha: National University of Defense Technology, 2014: 128-134 (in Chinese).

[61] VANLEER B. Towards the ultimate conservative difference scheme: V. A second-order sequel to Godunov’s method[J]. Journal of Computational Physics, 1979, 32(1): 101-136.

[62] ZHANG F, LIU J, CHEN B, et al. Evaluation of rotated upwind schemes for contact discontinuity and strong shock[J]. Computers and Fluids, 2016, 134(1): 11-22.

[63] WILSON G J, MACCORMACK R W. Modeling supersonic combustion using a fully implicit numerical method[J]. AIAA Journal, 1992, 30(4): 1008-1015.

[64] ZELDOVICH Y B. On the theory of the propagation of detonation in gaseous systems[J]. Journal of Experimental and Theoretical Physics, 1940, 10(5): 542-568.