粗糙元诱导的高超声速转捩机理及应用

2018-01-25 08:18朱德华袁湘江杨武兵

航空学报 2018年1期

朱德华，袁湘江，杨武兵

中国航天空气动力技术研究院，北京 100074

边界层转捩是高超声速飞行器设计中的重要气动问题，能够对飞行器气动力、气动热产生显著影响，也能对飞行稳定性、推进性能、翼舵控制效率等产生显著影响。粗糙元诱导边界层转捩(Roughness Induced Transition，RIT)一直是边界层转捩研究的难点问题，虽然RIT的研究已经有半个世纪的历史，但是高超声速RIT的物理机制至今仍未完全研究清楚。

关于RIT的理论研究方面开展得较早，物理机制的认识也在逐步加深。早在1962年，Van Driest 和 Blumer[1]针对圆锥光滑表面及球形粗糙元表面的转捩情况就进行了研究。研究发现对于光滑壁面情形转捩是随着雷诺数的增加而前移的。在这个情形下，转捩完全是由来流中的扰动引起的。随着雷诺数的进一步增加，会出现“临界条件”，此时粗糙元诱导的扰动要比自由来流的扰动影响重要。研究指出“有效点”是存在的，此时粗糙元可以完全独立地诱导边界层转捩，自由来流的扰动作用是可以被忽略的。2009年，Danehy等[2]利用一氧化氮平面激光诱导荧光(NOPLIF)的方法，获得了半球和圆柱两种类型的粗糙元绕流的流动细节。2011年，Tirtey等[3]利用红外热图和油流技术，获得了钻石型、斜坡型、圆柱型及圆球型粗糙元绕流的流场转捩特征。2012年，Wheaton 和 Schneider[4]在静音风洞中，利用皮托探针、热线探针和壁面脉动压力传感器获得了圆柱型粗糙元绕流的非定常特征，发现了诱导马蹄涡失稳的主导频率大约为21 kHz。

在数值计算方面，2010年，Bartkowicz等[5]采用直接数值模拟(Direct Numerical Simulation，DNS)方法探索了粗糙元上游扰动的产生和扰动向下游的发展。通过对流动细节的刻画，发现大尺度和小尺度粗糙元的失稳区域大小是不一致的。2013年和2014年，Duan等[6-7]采用DNS方法针对圆柱和斜坡型粗糙元诱导的高超声速边界层转捩进行了研究。针对圆柱型粗糙元，发现圆柱两侧的流动率先失稳，中心线处稍后失稳，并获得了诱导马蹄涡失稳的主导频率大约为19.23 kHz，与试验获得的21 kHz基本吻合。针对斜坡型粗糙元，发现其失稳主要是出现在中心线处，并将计算结果与试验结果进行了定性对比，基本吻合。2016年，段志伟和肖志祥[8]针对不同形状粗糙元诱导转捩的现象开展了研究，其研究表明强制转捩主要由粗糙元顶部的三维剪切层失稳导致，同时获得了斜坡型粗糙元的斜坡角度和间距对转捩的影响规律。2016年，赵晓慧等[9]针对高超声速进气道强制转捩流动开展了大涡模拟研究，研究发现强制转捩流动中的流向涡对存在偶模式和奇模式失稳。

综上所述，目前对高超声速条件下RIT的机理认识还十分欠缺。在风洞试验方面，噪声度的影响及精细试验手段的限制等因素使得认识RIT物理机制十分困难。在数值计算方面，高精度、高鲁棒性的数值方法及大规模并行计算技术是研究RIT物理机制的关键问题。

近些年有关RIT在工程应用方面开展了大量的研究工作，主要的研究对象是高超声速飞行器，如采用吸气式超燃冲压发动机的高超声速飞行器。这种飞行器前体的下表面是发动机进气道的一部分，通过进气道对来流空气进行压缩，达到超声速燃烧所需的压力和温度。但是，在层流状态下，进气道容易出现流动分离，产生溢流，减少进气道的捕获流量，造成进气道总压恢复系数变低，甚至造成进气道不起动进而导致飞行失败。研究发现湍流能够有效抑制流动分离，能够在很大程度上缓解上述不利状况。但另一方面，进气道流动如果过早地转捩为湍流，又将引起飞行器摩阻的增加。因此，前体与进气道必须设计合适的转捩位置，在保证进气道入口为湍流状态的前提下，尽量减少湍流区域。为此，需要针对吸气式高超声速飞行器的RIT开展相关研究。

从国外目前的研究情况来看，RIT在HIFiRE[10]项目试验飞行器、X-43A[11]与X-51[12]飞行器中都得到应用。

2000年，针对Hyper-X模型进行了RIT试验，试验模型为进气道压缩楔面。试验研究了粗糙元形状和主要尺寸参数对转捩的影响。图1为主要的粗糙元结构示意图[13]，图中“TBD”指可变化的粗糙元高度。马赫数为7、单位雷诺数为5.6×106/m下的试验结果表明，随粗糙元高度的增加，流动转捩位置前移。对比最高尺寸的钻石结构和后掠斜坡结构，后者效果稍差于前者，但其最小的结构和湍流旋涡的持续性以及潜在的加热性能较好。马赫数为7的飞行条件下，k/δ=0.6为诱导转捩的有效高度(其中k为粗糙元高度，δ为粗糙元位置边界层厚度)。

2010年，X-43A进气道强制转捩采用了如图1中Trip 2c所示的后掠结构[14]，其目的是在前体翼展方向引入涡发生器，促进发动机进气道前的边界层转捩。试验也表明，必须在前体进气道前加入人工强制转捩装置，以促进发动机进气道内流动为全湍流。

HIFiRE项目也针对钻石粗糙元诱导转捩问题开展了研究，如图2所示[15]。研究表明，在有效粗糙元尺寸之后，粗糙元的效果并不随平面尺寸的变化而急剧变化。

图1 Hyper-X中钻石以及斜坡绊点示意图[13]Fig.1 Trip (diamond and ramp) sketch of Hyper-X [13]

图2 HIFiRE项目绊点试验模型[15]Fig.2 Trip test model of HIFiRE Plane [15]

国内对RIT的试验研究很少，沈清等[16-17]根据三维波亚谐共振原理，设计了一种强制转捩装置。在FD-07风洞，马赫数为6的试验表明：在设计状态下，没有强制转捩装置的进气道不起动；加入强制转捩装置后，进气道起动。赵慧勇等[18]针对吸气式高超声速进气道设计了钻石型强制转捩装置。在FL-31高超声速风洞分别开展了进气道的自然转捩和强制转捩风洞试验，试验马赫数为5、6和7。其通过红外热图方法证实了钻石型强制转捩装置的有效性，获得了钻石型强制转捩装置的有效高度。

从RIT的工程应用中可以看出，RIT机理研究的欠缺已经开始制约了强制转捩在工程中的应用。在强制转捩的工程研究中粗糙元的外形、几何尺寸以及分布等的设计均需要理论支撑，然而目前国际和国内高超声速飞行器强制转捩装置的研究大多数是飞行试验和风洞试验的验证性研究，并未有理论支撑。

本文认为通过高超声速粗糙元诱导转捩的机理研究可以为高超声速飞行器的强制转捩设计提供理论支撑，同时可以改进现有的强制转捩设计方案的适用范围。在此基础上可以设计出一种新型的低阻力、小尺度、低热流的适用范围更大的强制转捩装置。因此，本文将针对不同类型强制转捩装置的诱导转捩机理开展研究，同时提出一种新型强制转捩控制装置，研究其诱导转捩机理以及其诱导转捩的效果。

1 控制方程和数值方法

控制方程为曲线坐标系下三维可压缩Navier-Stokes方程[19],采用高精度直接数值模拟方法求解该方程。对于空间离散，无黏项采用五阶WENO(Weighted Essentially Non-Oscillatory)格式[20]，黏性项采用六阶中心差分。时间离散采用三阶TVD(Total Variation Diminishing) Runge-Kutta方法[21]。

壁面处采用等温无滑移边界条件，入口剖面的选取是通过二维平板直接数值模拟得到的，展向是周期边界条件，出口是超声速出口条件。

2 计算结果分析

对于转捩机理的研究选取的计算条件为：马赫数Ma=6，雷诺数Re=2.6×107，来流温度T∞=70 K，壁面温度TW=300 K，雷诺数Re以1 m为特征长度。

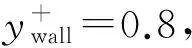
图3 粗糙元模型示意图Fig.3 Sketch of roughness element models

图4 对齿型强制转捩装置模型及尺寸示意图Fig.4 Sketch of model and size of “gear” forced-transition device

在工程应用方面，首先针对飞行条件进行分布式粗糙元诱导转捩的机理验证，具体条件为：Ma=6,Re=4.228×106,T∞=222.544 K,TW=500 K,迎角α=4°。

其次为了验证新型对齿型粗糙元的设计思想和有效性，选取风洞试验条件进行研究，具体条件为：Ma=6.36,Re=6.2×106,TW=300 K,α=-2°。

2.1 斜坡型粗糙元诱导转捩机制及应用

为了揭示斜坡型粗糙元诱导转捩的物理机制，本文选取机理研究的计算条件进行直接数值模拟研究，将从拓扑结构稳定性和边界层流动稳定性两个方面进行分析。

图5 斜坡型粗糙元附近摩擦力线分布Fig.5 Distribution of friction lines around ramp roughness element

针对直接数值模拟结果的拓扑结构稳定性分析是借助拓扑结构稳定性理论来开展的。图5显示的是斜坡型粗糙元附近的摩擦力线和相应的奇点分布。在粗糙元的头部区域,流动遇到粗糙元会向上游形成一部分回流，此时会在粗糙元上游区域的中心线处形成鞍点S1，另一部分流动是沿着粗糙元表面发展的，两侧的流动与头部区域的流动相互干扰在粗糙元表面形成了一个不稳定的结点N1。因此，可以看出斜坡粗糙元前部流动失稳是由于不稳定结点和中心处鞍点造成的。在粗糙元的底部区域由于经过粗糙元两侧后气流开始膨胀，在压差的作用下其底部会出现分离，在拓扑结构上会出现两个对称的稳定焦点F1和F1。流动继续向粗糙元的近尾迹区发展，可以看出流动经过分离区后，由于两侧的压力高于中心线处压力，在压差的作用下流动再次被压缩，这样在拓扑结构上出现了两个关于中心线对称的鞍点结构(S2和S3)，同时在中心线处相应地出现了一个不稳定结点N2。这样3个奇点结构组合成了鞍点-结点-鞍点(Saddle-Node-Saddle point, SNS)轨线结构，图5中的Zone 1放大图清晰地显示了SNS轨线结构的构成。根据拓扑结构稳定性理论可知，SNS轨线结构是不稳定的，其在扰动存在的情况下同样会向着非定常、非对称的振荡结构发展。由此可以得出在扰动存在的情况下，粗糙元中心线附近流动结构的失稳是由于SNS轨线结构造成的。

图6 斜坡型粗糙元的Q等值面Fig.6 Iso-surface of Q criterion of ramp roughness element

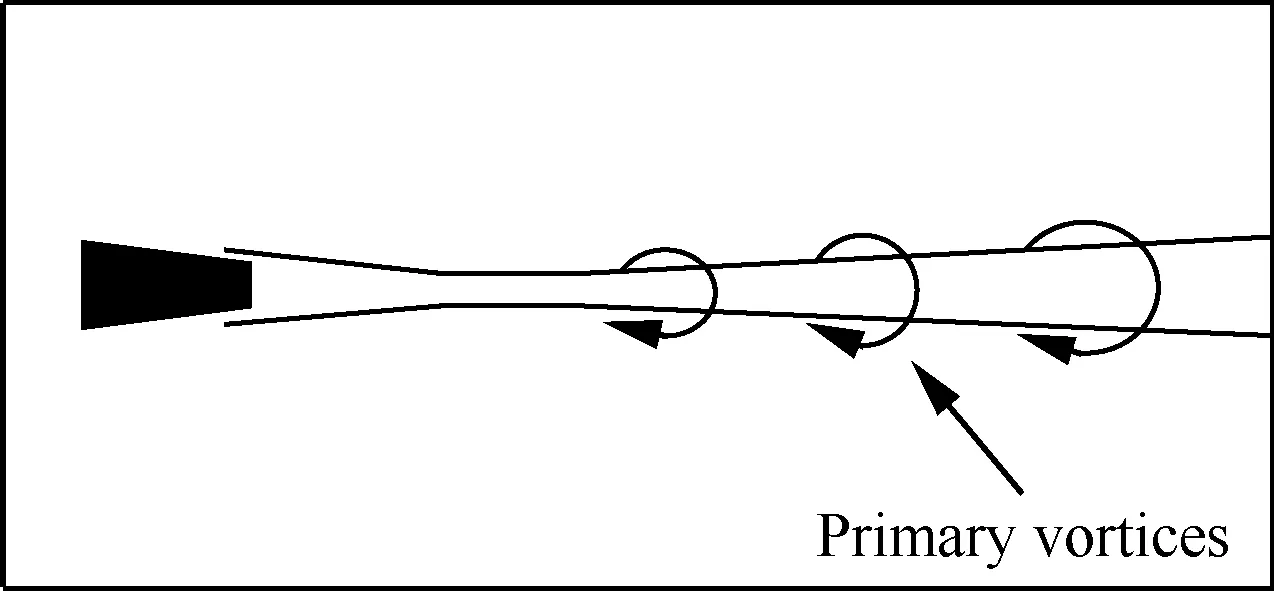
图7 斜坡型粗糙元涡结构示意图Fig.7 Sketch of vortex structure of ramp roughness element

下面针对斜坡型粗糙元进行边界层流动稳定性分析。图6为粗糙元速度梯度二阶不变量Q等值面图。图7给出了其尾迹区域失稳模式示意图，结合图6显示的结果可以看出，斜坡型粗糙元分离区后的主涡结构在中线附近率先开始出现失稳，发卡涡在自诱导及平均流的作用下迅速形成发卡涡串、发卡涡包，最终在尾迹下游区域流动变为全湍流状态。斜坡型粗糙元只存在主涡失稳一种模式。

通过上面斜坡型粗糙元诱导转捩机理的认识，可以发现斜坡型粗糙元只存在主涡失稳模式。为了增强其诱导转捩的能力，需要加快主涡结构的失稳，这里有两种有效的途径:① 增加粗糙元高度，但高度的增加会带来额外的波阻、摩阻以及高热流; ② 采用分布式粗糙元，每个斜坡粗糙元充分靠近，让不同的斜坡粗糙元的主涡结构出现相互作用以达到加速主涡结构失稳的效果。

通过对斜坡型粗糙元诱导转捩机理的认识，本文在类X-43飞行器前体外形上距前缘400 mm位置处安装了分布式斜坡型粗糙元(尺寸及分布参见图1)，在真实飞行条件下验证粗糙元诱导转捩的机理。通过数值模拟获得模型中心对称线上距前缘400 mm处边界层厚度为3.167 mm(利用总焓的99%定义边界层厚度)，此时分布式斜坡型粗糙元的高度取为2.2 mm。工程化的粗糙元转捩判据需要利用当地基于粗糙元尺寸的雷诺数，因此定义当地基于粗糙元尺寸的雷诺数为[22]

式中：k为粗糙元高度；下标k指的是没有粗糙元情形下，粗糙元高度处的物理量;ρk为密度;uk为速度;μk为黏性系数。对于斜坡型粗糙元,在飞行条件下Rek≈2 490。

图8 斜坡型强制转捩装置模型及Q等值面Fig.8 Model of ramp forced-transition device and iso-surface of Q criterion

图9 斜坡型粗糙元局部压力以及马赫数等值线图Fig.9 Contours of local pressure and Mach number around ramp roughness element

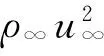
2.2 对齿型粗糙元诱导转捩机制及应用

研究表明，不同类型粗糙元具有不同的诱导转捩机理。这些机理的认识可以指导粗糙元外形和分布的设计。本文基于不同类型粗糙元诱导转捩机理，设计了一种对齿型粗糙元(如图4所示)。设计目标是新型粗糙元具有低阻力、小尺度、低热流的特点，同时在工程上能拓宽飞行适用范围。设计原理是利用斜坡型粗糙元低阻力、低热流的优点，同时利用钻石型粗糙元[23]存在主涡失稳和次涡失稳多种失稳模式的特点(如图10所示)，在对齿型粗糙元展向设计不同宽度的流动通道，从而在展向形成一定的压力梯度加强涡结构的失稳，此时对齿型粗糙元的高度和尺度可以很小。

下面针对对齿型粗糙元的直接数值模拟结果分别进行拓扑结构稳定性分析和边界层流动稳定性分析，验证本文的设计原理。

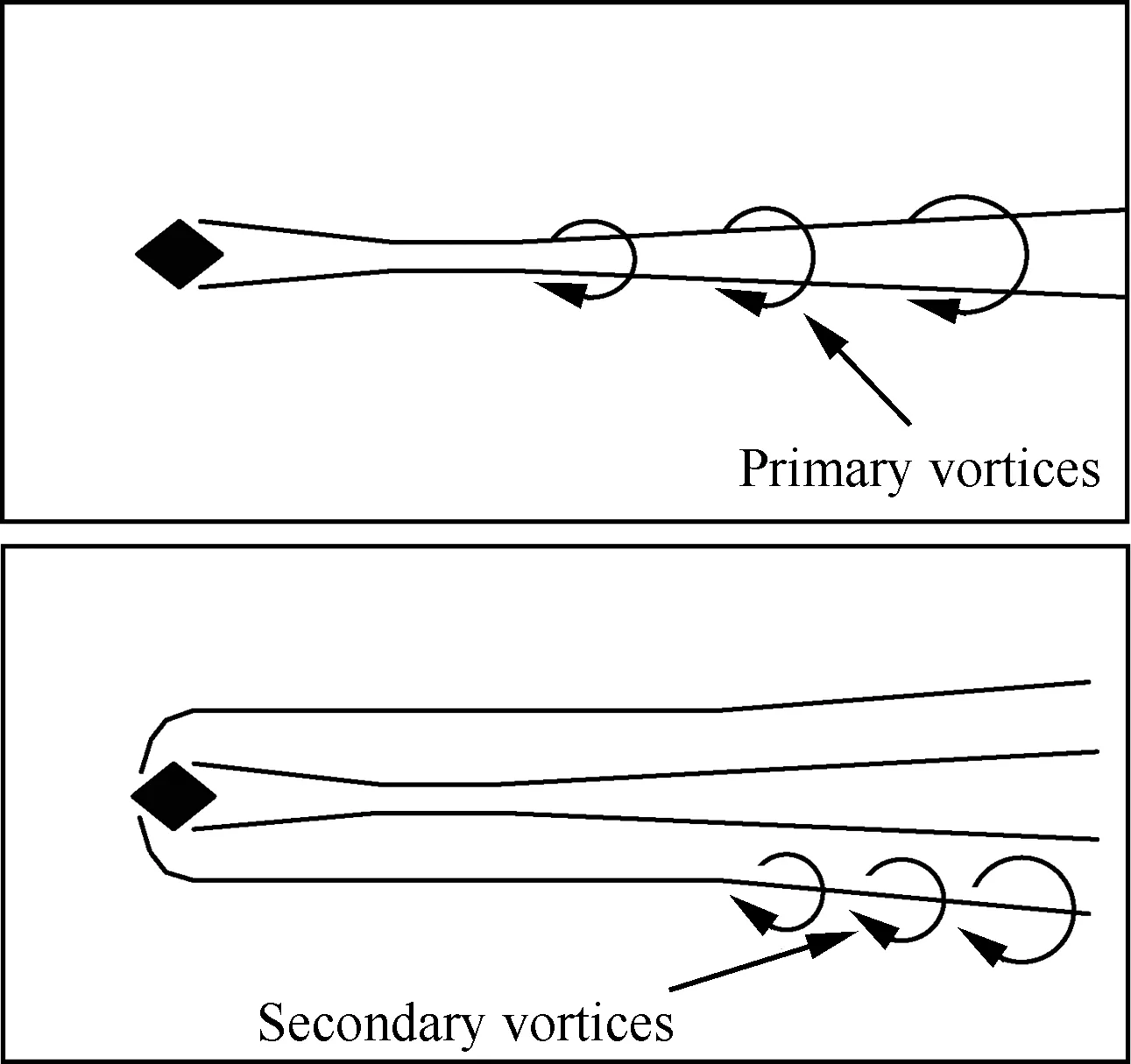
图10 钻石型粗糙元涡结构示意图[23]Fig.10 Sketch of vortex structure of diamond roughness element [23]

图11 对齿型粗糙元附近摩擦力线分布Fig.11 Distribution of friction lines around “gear” roughness element

图11显示的是对齿型粗糙元附近的摩擦力线和相应的奇点分布。可以看出对齿型粗糙元头部奇点的形成与分布和斜坡型粗糙元是类似的。对齿型粗糙元中间的斜坡型流动通道的中心会形成一个鞍点S1，这是由绕过粗糙元的流动和收缩通道内的回流形成的。沿着收缩通道压力会增加，而底部存在分离区压力降低，这样就会在收缩通道内形成一个不稳定的结点N1。对比斜坡粗糙元可以看出，对齿粗糙元的前部流动失稳同样是由于不稳定结点和中心处鞍点造成的。在对齿粗糙元的底部区域由于经过粗糙元两侧后气流开始膨胀，在压差的作用下其底部会出现分离，上半部分的拓扑结构上会出现两个稳定焦点F1和F2，下半部分与上半部分对称，同样会出现两个稳定焦点F3和F4。流动继续向粗糙元的近尾迹区发展，可以看出流动经过分离区后，由于两侧的压力高于中心线处压力，在压差的作用下流动再次被压缩，这样在对齿型粗糙元的上半部分和下半部分的拓扑结构上会出现两个关于中心线对称的鞍点结构(S2和S3)，结合收缩通道内的不稳定结点N1，这样3个奇点结构同样组成了SNS轨线结构，图11中的Zone 1放大图清晰地显示了粗糙元底部附近的轨线结构构成。此时的SNS轨线结构也是不稳定的，由于对齿型粗糙元的设计原理是利用展向的压力梯度，因此SNS轨线结构的不稳定性会加剧，使得对齿型粗糙元流动结构加速失稳。

图12 对齿型粗糙元的Q等值面Fig.12 Iso-surface of Q criterion of “gear” roughness element

图13 对齿型粗糙元涡结构示意图Fig.13 Sketch of vortex structure of “gear” roughness element

对于对齿型粗糙元，图12为粗糙元速度梯度二阶不变量Q等值面图。图13给出了其尾迹区域失稳模式示意图，结合图12显示的结果可以看出，对齿型粗糙元分离区后的主涡结构分为两部分，分别为上部分的主涡结构以及下部分的主涡结构，两部分的主涡结构随着流向距离的增加均开始出现失稳，同时由于对齿型粗糙元展向压力梯度的存在，两部分主涡结构的相互作用会加剧，在流动下游区域两部分失稳的主涡结构会在相互干扰下，形成一个大的失稳主涡结构，此结构的失稳会使得展向很大一部分区域完全演化为全湍流。

通过对对齿型粗糙元的诱导转捩机理的研究可以看出，本文的设计原理是正确的。对齿型粗糙元利用了斜坡型粗糙元低阻力、低热流的优点，同时可以看出由于其前缘尺寸更小，流动在粗糙元前缘形成回流很少，对齿型粗糙元相比于斜坡型粗糙元阻力更小、热流更低。对齿型粗糙元还利用了钻石型粗糙元存在多种失稳模式的特点，在对齿型粗糙元后形成了两个对称的主涡结构，通过在对齿型粗糙元展向设计不同宽度的流动通道，形成展向压力梯度，加强了主涡结构的相互作用，使其诱导转捩能力增强。

为了验证对齿型粗糙元的诱导转捩效果，在类X-43飞行器前体外形上距前缘400 mm位置处安装分布式对齿型粗糙元。

首先针对真实飞行条件开展研究，此时分布式斜坡型粗糙元的高度取为1.6 mm。同样可以给出当地基于粗糙元尺寸的雷诺数Rek≈1 510。

图14为分布式对齿型粗糙元模型以及Q等值面图，从图14中可以看出，即使在对齿型粗糙元尺度很小的情况下，粗糙元后的流向涡结构的演化和破碎同样十分迅速，其诱导转捩能力仍然很强，其失稳模式和失稳机理与上面的分析是一致的。

为了与斜坡型粗糙元附近的流动以及激波结构进行对比，图15给出了中心对称线位置处的粗糙元附近的无量纲压力以及马赫数等值线图，从图中可以看出，由于对齿型粗糙元相对尺度较小，因此其处于超声速区的高度较少，其自身产生的波系结构以及压力变化程度相比斜坡型粗糙元要弱。

上面的机理研究只是定性地研究了粗糙元诱导转捩的机理和应用效果，为了证实本文的计算方法以及新型粗糙元设计思想的正确性，下面针对风洞试验条件下的分布式粗糙元诱导转捩进行定量的对比研究。

风洞试验的类X-43模型是全尺寸模型，试验模型包括光滑模型、安装分布式斜坡型粗糙元的模型以及安装对齿型粗糙元的模型。分布式粗糙元的安装位置为距模型前缘0.4 m处。

图14 对齿型强制转捩装置模型及Q等值面图Fig.14 Model of “gear” forced-transition device and iso-surface of Q criterion

图15 对齿型粗糙元局部压力以及马赫数等值线图Fig.15 Contours of local pressure and Mach number around “gear” roughness element

图16 不同粗糙元模型的直接数值模拟和风洞试验热流分布Fig.16 Heat flux distributions of DNS and wind tunnel test around roughness elements of different types

风洞试验结果以及直接数值模拟结果显示在图16中。图16显示的是类X-43模型中心对称面处的归一化壁面热流qw(以距前缘0.2 m处的壁面热流为归一化参考值)随流向距离的变化规律。正方形符号的曲线是风洞试验中未安装分布式粗糙元的光滑表面试验结果，可以看出不安装分布式粗糙元时在类X-43模型的前体是未发生转捩行为的，为层流状态。圆形符号的曲线是风洞试验中安装分布式斜坡型粗糙元的试验结果，斜坡型粗糙元的高度为h=0.7δ。从曲线中可以看出，流动经过粗糙元后热流曲线稍有下降然后迅速升高，可以认为其发生了转捩行为，大约在距前缘0.64 m位置实现全湍流状态。三角形符号的曲线是风洞试验中安装分布式对齿型粗糙元的试验结果，对齿型粗糙元的高度为h=0.5δ，对齿型粗糙元的高度要低于斜坡型粗糙元。从曲线中可以看出，流动经过粗糙元后热流曲线迅速抬升，转捩发生，大约在距前缘0.6 m位置实现全湍流状态。从对齿型和斜坡型粗糙元试验结果的对比可以看出，高度低的对齿型粗糙元转捩反而靠前，这证明了本文新型粗糙元设计的有效性和合理性。需要指出的是图16的风洞试验结果中，对齿型粗糙元转捩过程中的热流峰值高于斜坡型粗糙元转捩过程中的热流峰值。这是由于测量热流的传感器是有一定直径的，所测结果为展向一定范围内的热流平均值，而由于对齿型粗糙元转捩较早，展向区域同样转捩靠前，这样的一定区域的展向热流均值是会高于斜坡型粗糙元的。直接数值模拟结果显示中心对称线上对齿型粗糙元转捩过程中的热流峰值低于斜坡型粗糙元，这和对齿型粗糙元高度较低，带来的附加热流小的规律是一致的。

另外，从图16中可以看出直接数值模拟结果(斜坡型粗糙元与对齿型粗糙元)与风洞试验结果基本吻和，转捩起始位置和转捩发展规律基本一致，全湍流区的热流值略高于风洞试验结果。直接数值模拟结果和风洞试验结果转捩起始位置能够较好地吻和是由于粗糙元的高度超过了各自的临界设计高度，粗糙元本身可以独立诱导转捩发生，受来流扰动影响较小。直接数值模拟结果和风洞试验结果的对比证明了本文采取的数值模拟方法以及网格划分的可靠性。

综上所述，可以看出对齿型粗糙元与斜坡型粗糙元均具有低阻力、低热流的特点，但相比于斜坡型粗糙元，对齿型粗糙元具有多种涡结构失稳模式，其展向不同宽度的流动通道，可以形成压力梯度以此加强涡结构的失稳，因此在同样的几何高度尺度下对齿粗糙元具有更强的诱导转捩能力。在工程应用中，由于对齿型粗糙元的有效高度更低，飞行器上布置对齿型粗糙元的尺度相比斜坡型粗糙元会更小，因此附加的摩阻和热流更低，带来的额外损失更少。此外，在同样的几何高度尺度下，对齿型粗糙元相比斜坡型粗糙元能够有效诱导转捩对应的飞行范围更广。

3 结论

本文采用直接数值模拟(DNS)的方法，针对不同类型粗糙元诱导的高超声速边界层转捩机理开展了研究，从拓扑结构稳定性和边界层流动稳定性两个角度分析了不同类型粗糙元诱导转捩的机理。通过不同类型粗糙元诱导转捩机理的研究，设计了一种对齿型粗糙元，其具有小尺度、低摩阻、低热流、诱导转捩能力强的特点。同时针对斜坡型以及对齿型粗糙元的工程应用开展了研究，验证了不同类型粗糙元诱导转捩的机理，为强制转捩装置设计提供了基础理论支撑。

1) 不同类型粗糙元均同时存在拓扑结构失稳效应和边界层流动失稳效应两种类型的失稳效应。

2) 不同类型粗糙元底部区域均存在鞍点-结点-鞍点(SNS)型轨线，在扰动的作用下其会形成非定常、非对称的振荡结构。

3) 对齿型粗糙元具有小尺度、低摩阻、低热流、诱导转捩能力强的特点。对齿型粗糙元的有效高度更低，在同样的几何高度尺度下，对齿型粗糙元相比斜坡型粗糙元能够有效诱导转捩对应的飞行范围更广。

[1] VAN DRIEST E R, BLUMER C B. Boundary-layer transition at supersonic speeds-three dimensional roughness effects (spheres)[J]. Journal of the Aerospace Sciences, 1962, 29(8): 909-916.

[2] DANEHY P M, BATHEL B F, IVEY C B, et al.No PLIF study of hypersonic transition over a discrete hemispherical roughness element: AIAA-2009-0394[R]. Reston， VA: AIAA, 2009.

[3] TIRTEY S C, CHAZOT O, WALPOT L. Characterization of hypersonic roughness-induced boundary-layer transition[J]. Experiments in Fluids, 2011, 50(2): 407-418.

[4] WHEATON B M, SCHNEIDER S P. Roughness-induced instability in a hypersonic laminar boundary layer[J]. AIAA Journal， 2012, 50(6): 1245-1256.

[5] BARTKOWICZ M D, SUBBAREDDY P K, CANDLEER G V. Numerical simulations of roughness induced instability in the Purdue Mach 6 wind tunnel: AIAA-2010-4723[R]. Reston, VA: AIAA, 2010.

[6] DUAN Z W, XIAO Z X, FU S. Direct numerical simulation of hypersonic transition induced by a cylindrical roughness element: AIAA-2013-3112[R]. Reston，VA: AIAA, 2013.

[7] DUAN Z W, XIAO Z X, FU S. Direct numerical simulation of hypersonic transition induced by a ramp roughness element: AIAA-2014-0237[R]. Reston，VA: AIAA, 2014.

[8] 段志伟，肖志祥.粗糙元诱导的高超声速边界层转捩[J]. 航空学报， 2016， 37(8)： 2454-2463.

DUAN Z W, XIAO Z X. Roughness element induced hypersonic boundary layer transition[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2454-2463 (in Chinese).

[9] 赵晓慧, 邓小兵, 毛枚良, 等. 高超声速进气道强制转捩流动的大涡模拟[J]. 航空学报， 2016， 37(8): 2445-2453.

ZHAO X H, DENG X B, MAO M L, et al. Large eddy simulation for forced transition flow at hypersonic inlet[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2445-2453 (in Chinese).

[10] KIMMEL R, ADAMCZAK D, GOSSE R, et al. Ground test and computation of boundary layer transition on the hypersonic international flight research and experimentation HIFiRE-5 vehicle: AFRL-RB-WP-TR-2011-3025[R]. White Paterson, OH: AFRL, 2011.

[11] BERRY S A, DARYABEIGI K, WURSTER K, et al. Boundary layer transition on X-43A: AIAA-2008-3736[R]. Reston， VA: AIAA, 2008.

[12] BORG M P. Laminar instability and transition on the X-51[D].West Lafayette, IN: Purdue University, 2009: 21-31.

[13] BERRY S A, AUSLENDER A H, DILLEY A D, et al. Hypersonic boundary-layer trip development for Hyper-X:AIAA-2000-4012[R]. Reston， VA: AIAA, 2000.

[14] BERRY S, DARYABEIGI K, WURSTER K, et al. Boundary-layer transition on X-43A[J]. Journal of Spacecraft and Rockets, 2010, 47(6): 922-934.

[15] KIMMEL R L. Roughness considerations for the HIFiRE-1 vehicle:AIAA-2008-4293[R]. Reston，VA: AIAA, 2008.

[16] 赵俊波，沈清，张红军，等. 基于T-S波谐频共振的超燃进气道边界层转捩[J]. 航空动力学报， 2010, 25(11): 2420-2424.

ZHAO J B, SHEN Q, ZHANG H J, et al. Boundary transition research of scramjet inlet based on the Tollmien-Schlichting (T-S) wave syntony[J]. Journal of Aerospace Power, 2010, 25(11): 2420-2424 (in Chinese).

[17] 张红军，沈清. 新型高超声速进气道边界层人工转捩方法研究[J]. 实验流体力学， 2016, 30(2): 75-78.

ZHANG H J, SHEN Q.A new method of artificial boundary layer transition for hypersonic inlet[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 75-78 (in Chinese).

[18] 赵慧勇，周瑜，倪鸿礼, 等. 高超声速进气道边界层强制转捩试验[J]. 实验流体力学， 2012, 26(1): 1-6.

ZHAO H Y, ZHOU Y, NI H L, et al. Test of forced boundary-layer transition on hypersonic inlet[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 1-6 (in Chinese).

[19] 沈清，朱德华. 高超声速尾迹流场稳定性数值研究[J]. 力学学报， 2009， 41(1): 1-7.

SHEN Q, ZHU D H. Numerical study of the stability of hypersonic wake[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1): 1-7 (in Chinese).

[20] JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228.

[21] 张涵信，沈孟育. 计算流体力学——差分方法的原理和应用[M]. 北京：国防工业出版社， 2003: 289-292.

ZHANG H X, SHEN M Y. Computational fluid dynamics—Fundamentals and applications of finite difference methods[M]. Beijing: National Defence Industry Press, 2003: 289-292 (in Chinese).

[22] JOEL E G, NICHOLAS J B, JONATHAN P. High fidelity computational study of the HIFiRE-1 boundary layer trip: AIAA-2014-0433[R]. Reston， VA: AIAA, 2014.

[23] 朱德华，袁湘江，沈清，等. 高超声速粗糙元诱导转捩的数值模拟及机理分析[J]. 力学学报， 2015， 47(3)： 381-388.