面向非结构混合网格高精度阻力预测的梯度求解方法

张培红，张耀冰，周桂宇，陈江涛，邓有奇

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

阻力的高精度预测对于现代飞行器的设计，特别是民用飞机和运输类飞机的设计极其重要。一直以来，国外就十分重视CFD计算方法的阻力预测能力。为评估CFD阻力预测能力的发展现状，AIAA应用空气动力学技术委员会举办了一系列阻力预测研讨会[1-5]，截止目前，AIAA阻力预测研讨会已经举办了6届，为世界范围内的大学、研究所和工业部门共同评估当前CFD方法预测运输类飞行器跨声速流场气动力和力矩系数的发展水平，提供了一个公平的平台，从而促进了CFD应用水平的提高。

随着计算机技术的不断发展，CFD在湍流模型、网格技术、数值算法、可视化、并行计算等方面取得飞速发展，已成为型号设计部门的常规手段之一[6-9]。特别是非结构网格生成技术的迅速发展，减少了网格生成人工工作量，大大提高了网格对复杂构型的适应能力和灵活性，推动了CFD解决复杂工程问题的能力[10-13]。但是，由于非结构网格在黏性区域很难使用类似结构网格的大长宽比网格，导致阻力预测精度降低，严重阻碍了非结构网格的应用和发展[14-16]。因此，如何解决非结构网格阻力预测精度低与现代飞行器设计对阻力预测精度要求高的矛盾，是当前CFD领域亟需解决的关键技术和难题。

CFD计算过程中在网格单元面上重构标量的值，以及计算扩散项和速度导数时都需要用到梯度，因此梯度的求解对于非结构混合网格计算的精度和鲁棒性起非常重要的作用[17-22]。通常的梯度求解方法有Least-Squares方法和Green-Gauss方法，由于Least-Squares方法对于曲面大压缩比网格得到的结果很差，甚至会比实际值小一个量级，因此，Green-Gauss方法是目前应用最广的一种梯度求解方法[18]。Green-Gauss方法的关键是求解面心的值，其最大优点是与计算通量的过程相似，不需要增加新的数据结构，可以提高计算效率，但由于只使用了与当前单元共面的单元的信息，周围其他单元的信息并没有用到，在进行混合网格的梯度计算中存在缺陷，在不同类型单元交界处，得到的梯度变得极度不准确。为了克服Green-Gauss方法的缺点，提高计算准度，人们尝试对Green-Gauss方法进行了多种改进[18-22]。一种改进是采用距离或者体积进行加权，这种方法虽然在一定程度上可以提高计算的准度，但当面心不在体心的连线上时，计算精度会很不理想[20]。另一种改进是先按照Green-Gauss方法求出梯度的初值，然后采用迭代法进行迭代，得到最终梯度的值，这种方法可以较好地改进梯度计算的准确性，但是由于迭代运算，可能会导致产生严重的振荡[21]。Blazek进一步对Green-Gauss方法进行了改进[22]，他将与控制体有公共点的相邻控制体的体心相连，形成新的控制单元，并将形成的控制单元作为新的控制体。这种改进方法的缺点是需要增加一个新的基于单元的数据结构，用来提供体心和新控制体面之间的联系，因此，这种方法不再是网格透明的(与单元信息无关)，并且不能使用高效的循环[22]。

本文基于非结构混合网格梯度求解的特点，在传统的Green-Gauss梯度求解方法基础上，通过增加计算所用的谱，采用更多周围控制单元的信息，提出了一种适用于非结构混合网格黏性计算的节点型Green-Gauss梯度求解方法。通过DLR-F4翼身组合体改进方法前后的计算结果比较，验证了方法的有效性。采用改进后的梯度求解方法对第5届AIAA阻力预测研讨会的通用研究模型(Common Research Model，CRM)开展了详细的计算研究，进一步验证了改进方法的可靠性和阻力的预测能力。该方法克服了Green-Gauss方法和以往改进的Green-Gauss方法的缺点，提高了阻力的预测精度和程序的鲁棒性。

1 数值方法

本文计算采用了课题组自主开发的MFlow解算器。MFlow是基于非结构混合网格的用于求解亚跨超声速流场的专业CFD软件，软件编写采用模块化设计思想。非结构混合网格一般由四面体、六面体、三棱柱或者金字塔组成，本文在生成混合网格时，采用一种改进的推进层方法在物面黏性作用区生成大伸展比三棱柱形和金字塔形网格；在其他流动区域仍采用阵面推进方法生成四面体网格。这样既保持了非结构网格易于控制网格单元的大小、形状及网格点的位置，具有灵活性大，对复杂外形的适应能力强，并且可以方便地作自适应计算和大规模分布式并行计算等优点，又克服了非结构网格进行黏性计算时计算效率和计算精度低的缺陷。

采用有限体积法对空间进行离散，未知变量位于网格单元的体心。控制方程为守恒形式的非定常可压缩Navier-Stokes方程，即

(1)

式中：Ω为控制体的体积；∂Ω为控制体封闭面的面积；W为守恒变量；Fc为无黏通量；Fv为黏性通量。定义分别为

(2)

(3)

(4)

式中：(x,y,z)为笛卡儿坐标系下的坐标分量；(u,v,w)为笛卡儿坐标系下的速度分量；(nx,ny,nz)为微元面的单位法向矢量在笛卡儿坐标系下的分量；τij为切应力；ρ、p、E、H和V分别为密度、压力、总能量、总焓和速度。

本文采用三重“V”循环多重网格方法进行收敛加速，主控方程对流项采用二阶迎风Roe通量差分格式进行离散，黏性项采用中心差分格式离散。假定流场为完全湍流流场，湍流模型采用S-A一方程湍流模型[23]，湍流控制方程空间离散采用一阶迎风格式。主控方程和湍流方程时间迭代均采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法。在使用原始Green-Gauss方法和节点型Green-Gauss方法对计算结果影响分析时，采用Roe格式，Harten-Yee熵修正。

2 Green-Gauss方法及其改进

对于本文采用的格心型网格，Green-Gauss方法的公式为

(5)

(6)

式中：NF为离散的控制体Ω的面数；SIJ为第J个面方向向外的面积矢量；UIJ为第J个面的面心值；UI为控制体单元I的体心值；UJ为控制体单元J的体心值。

Green-Gauss方法的关键是求解面心值，式(6)中使用面左右单元的体心值来求面心值，其最大优点是与计算通量的过程相似，不需要增加新的数据结构，可以提高计算效率，但由于只使用了与当前单元共面的单元信息，周围其他单元的信息并没有用到，如图1所示，在进行混合网格的梯度计算中准度偏低。

为提高非结构网格中梯度的求解准度，针对传统Green-Gauss方法和Blazek改进方法求解梯度时存在的缺陷，本文提出了一种称为“节点型Green-Gauss方法”的梯度求解方法。其基本思想是：通过增加计算所用的谱，采用更多周围控制单元的信息来提高梯度求解的准度，计算过程中面心值用该面所有顶点的算术平均得到，而顶点值又利用它周围所有单元的体心值通过距离加权平均得到，这样就充分利用了周围控制体的所有已知信息，如图2所示。

假设控制体单元I,共有Ni个顶点，对于顶点i,有NI个相邻的控制体单元。采用改进后的方法求解控制体单元I的梯度时，首先求解控制体单元的顶点的值，对于顶点i,其值UIi由其相邻的控制单元的体心值通过距离加权得到，即

(7)

式中：diJ为顶点i相邻的第J个控制单元体心到顶点i的距离；UiJ为顶点i相邻的第J个控制单元的体心值。

控制体单元I的第J个面的面心值由式(7)中求得的顶点值算术平均得到,即

(8)

图1 Green-Gauss方法Fig.1 Green-Gauss method

图2 节点型Green-Gauss方法Fig.2 Node-based Green-Gauss method

式中：Nj为控制体单元I的第J个面的顶点个数。

最后把式(8)得到的面心值代入式(5)得到控制体单元I的梯度值。

3 算例验证

为验证改进后的梯度求解方法对计算结果的影响，本文对DLR-F4翼身组合体跨声速绕流流场进行了计算。DLR-F4[24-25]是一个典型的现代运输类飞机外形翼身组合体，具有大展弦比机翼和大型客机类型的机身，设计巡航马赫数为0.75，机身长1.192m,半展长0.5857m,机翼参考面积为0.1454m2,平均气动弦长为0.1412m,详细参数见文献[24]，在欧洲三大风洞ONERA-S2MA、NLR-HST和DRA-8ft×8ft (1ft=0.3048m)中进行了全面系统的试验研究，是目前检验雷诺-平均Navier-Stokes(RANS)流场解算器在复杂外形亚跨超声速流动中的模拟能力的一个很好的算例，作为算例，在AIAA第1届阻力研讨会上采用各种解算器进行了计算，并取得了一致的结果[2]。计算状态：马赫数Ma=0.75,迎角α=0°,雷诺数Re=3.0×106,其中雷诺数取基于机翼的平均气动弦长0.1412m。

图3为DLR-F4翼身组合体的计算网格示意图，图3(a)为表面网格和对称面网格，图3(b)为边界层网格。计算时采用半模进行计算，半模网格单元总数为2164万，其中四面体为1368万，三棱柱为795万。物面单元数为29.5万，物面法向三棱柱层数为27层，第1层间距约为1.0×10-6m(y+≈1),前4层单元采用相同的间距，从第5层开始，变化率为1.2。机翼后缘采用各向异性三角形网格，单元数为32个。远场边界取约50倍的机翼平均气动弦长。

图3 DLR-F4翼身组合体网格Fig.3 Grid of DLR-F4 wing-body configuration

表1给出了梯度求解方法改进前后阻力计算结果与其他软件和风洞试验结果比较。可以看出，所有软件计算结果都比试验值偏大，改进梯度求解方法后，阻力减小了23.4个阻力单位，与试验值更接近。

图5为方法改进前后不同站位y/b剖面压力系数Cp分布比较，c为弦长，由图可见，改进后的节点型方法计算得到的前缘吸力峰比较光滑，并且峰值大，而原始Green-Gauss方法计算得到的结果有跳跃；两种方法压力剖面的区别主要在前缘吸力峰和激波的位置，以及波后的激波边界层干扰区。由于这些位置都是流场变化剧烈的地方，梯度值较大，变化剧烈，对梯度的求解准度要求较高，准确求解这些位置的变量梯度非常重要。

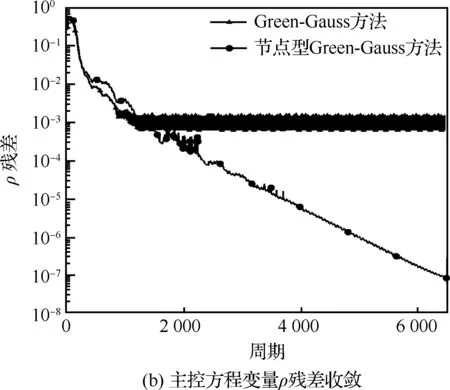
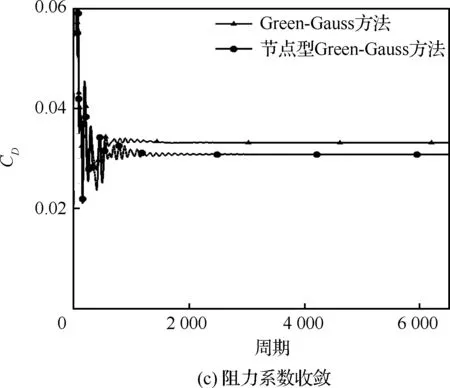
图4 梯度求解方法对收敛曲线的影响Fig.4 Influence of gradient calculation method on solution convergence

图6为方法改进前后得到的翼根后缘区域分离气泡的比较。很明显，两种方法计算得到的分离区域的大小和轮廓形状基本相同，改进后的方法计算得到的翼上的大涡略偏前一点，细节上刻画更明显，中间区域出现了两个小的分离气泡，说明改进后的方法计算精度更高。

表1 不同梯度求解方法对阻力系数的影响

图5 梯度求解方法对压力分布的影响Fig.5 Influence of gradient calculation method on pressure distribution

通过以上收敛曲线、阻力系数、压力分布和流场细节的对比分析可以看出，改进后的节点型方法可以更好地提高梯度的求解准度，更好地模拟梯度变化剧烈区域的压力分布特征以及流场细节特征，使计算过程收敛更好，阻力预测精度更高。

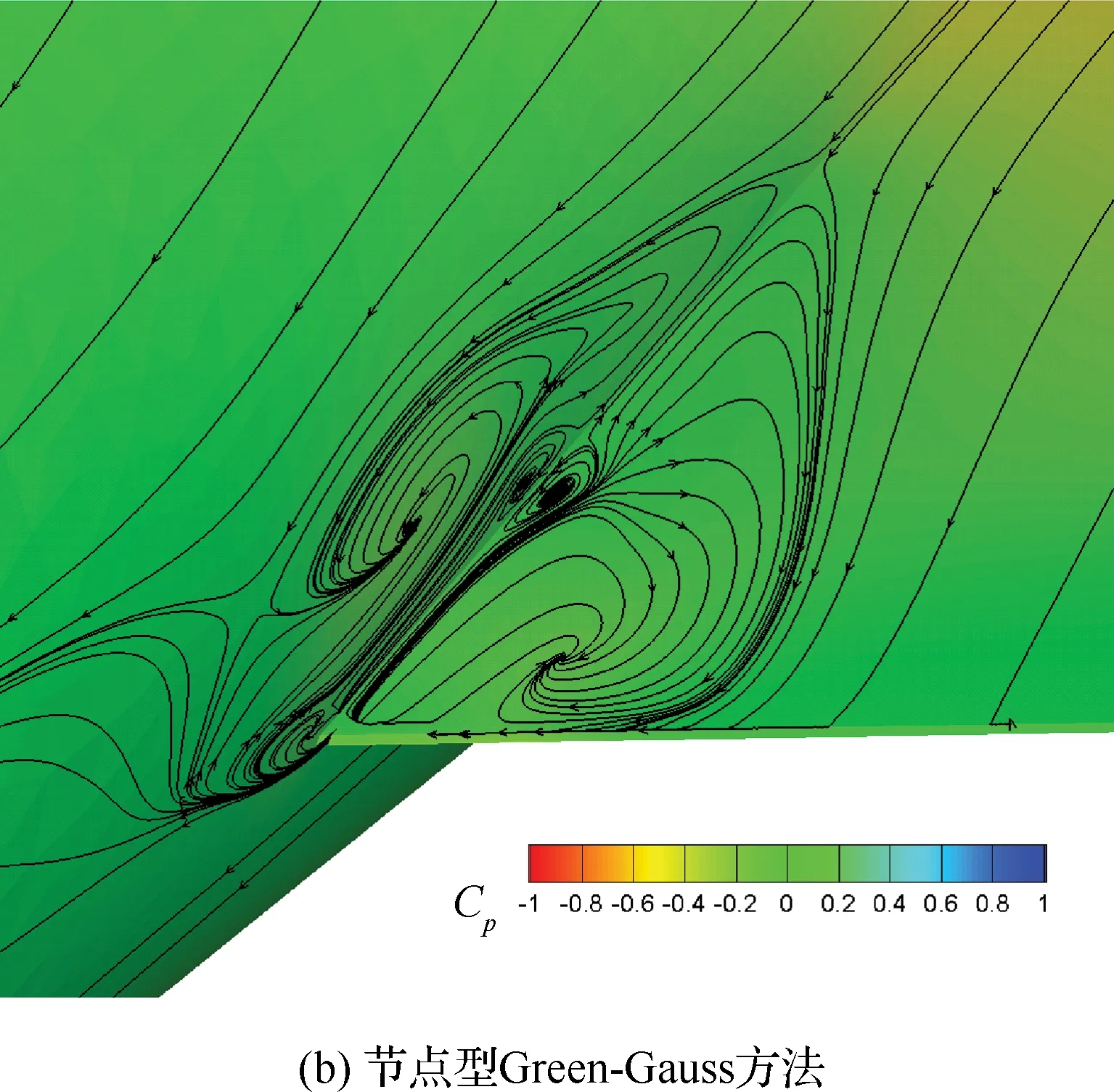
图6 梯度求解方法对分离气泡的影响Fig.6 Influence of gradient calculation method on separation bubble

4 数值模拟结果及分析

NASA的通用研究模型(CRM)是第5届AIAA阻力预测研讨会的计算外形，由机身和机翼组成，其中机身是典型的商业运输机机身，机翼是跨声速超临界机翼, CRM表面网格见图7。该外形在NASA Langley National Transonic Facility和NASA Ames 11-ft风洞都进行了详尽的试验，可以为各种CFD代码提供验证计算的标准数据。会议主办方针对CRM提供了包括多块结构网格、重叠网格和非结构网格在内的标准网格系列，分为六面体网格和三棱柱/四面体混合网格两种形式。六面体网格共有5套，网格单元数从638 976～40 894 464，分别用L1T、L2C、L3M、L4F、L5X表示。混合网格是在六面体网格的基础上生成的，在壁面附近将一个六面体剖分成两个三棱柱，在其他区域将一个六面体剖分成6个四面体，编号与剖分前的六面体网格相同，分别为L1T、L2C、L3M、L4F。

第5届AIAA阻力预测研讨会中，来自9个国家的22家单位针对该模型完成了阻力预测并提交了计算结果，对固定升力巡航状态的阻力预测能力进行了检验。计算状态：Ma=0.85,CL=0.500 0,Re=5.0×106。

首先对CRM进行了网格收敛性研究，主要目标是估算气动力的网格收敛解，也就是估计当网格量趋近于无穷大时气动力的值。表2和表3分别给出了不同六面体网格和混合网格计算得到的，在设计点CL=0.5时的迎角、升力、阻力等，并给出了NASA Langley National Transonic Facility的试验结果。从表3可以看出，计算得到的定升力迎角与试验值均有一定的差异。在前几届的阻力预测会议中也发现了这种情况。根据Shahyar和Neal[25]的分析， 差异产生的原因包括风洞洞壁干扰和阻塞影响、支架影响、气动弹性效应，机翼后缘钝度以及固定转捩的影响，因此这里比较定升力时的阻力更有意义。

图7 CRM表面网格(L1T)Fig.7 Surface grid of CRM (L1T)

表2 CRM六面体网格预测结果Table 2 Prediction results of CRM using hex grids

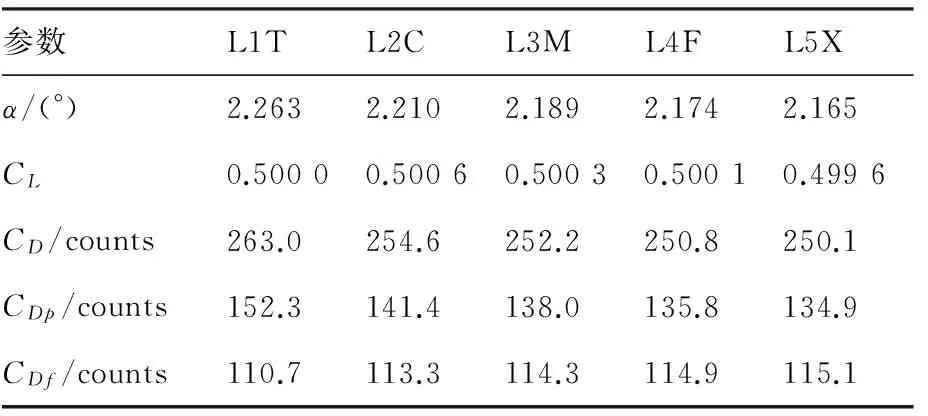
参数L1TL2CL3ML4FL5Xα/(°)2.2632.2102.1892.1742.165CL0.50000.50060.50030.50010.4996CD/counts263.0254.6252.2250.8250.1CDp/counts152.3141.4138.0135.8134.9CDf/counts110.7113.3114.3114.9115.1

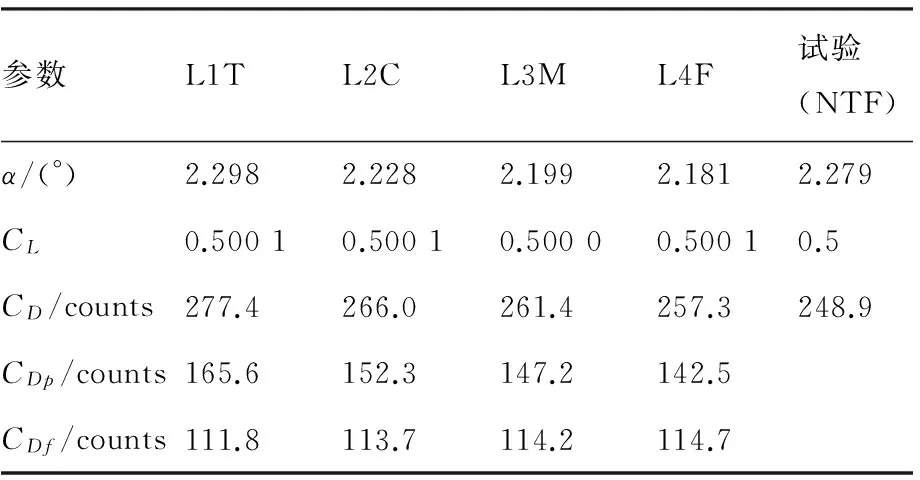
表3 CRM混合网格预测结果Table 3 Prediction results of CRM using hybrid grids

从表2可以看出，使用六面体网格时，L4F和L5X得到的阻力跟试验预测只有不到2 counts(1 counts=阻力系数0.000 1)的差别，达到了很高的阻力预测精度。由于混合网格是由同样编号的六面体网格经过剖分得到的，因此比较同样编号的六面体网格和混合网格，可以得到不同网格形式对阻力预测的影响。在本文的研究中发现，同样编号的混合网格预测的摩擦阻力系数CDf和六面体网格基本没有差别，但是预测的压差阻力系数CDp要比六面体网格稍大。

图8为采用六面体网格计算得到的阻力、压差阻力和摩擦阻力的网格收敛图，横坐标取N-2/3,N表示网格单元数，采用N-2/3是基于数值方法为二阶精度，对于由粗到细的一套自相似网格，表示其网格尺寸的二次方，因此直线就表示空间网格收敛为二阶精度，N-2/3为0时表示网格量为无穷大。由图可见，当网格量趋于无穷时阻力收敛是单调的，而且收敛精度接近二阶。压阻随网格加密减小，而摩阻随网格加密增大，由于压阻减小得多，因而总阻力也随网格加密而减小。

图9给出了第5届阻力会议组委会统计的阻力预测值柱状图[26]，包括OVERFLOW、FLUENT、CFD++、EDGE、FUN3D、HIFUN、NSU3D、TAU等知名CFD软件的计算结果，以及NTF风洞和Ames风洞的试验结果。柱状图中给出的各软件的计算结果是采用Richardson外插方法[27]进行网格收敛性分析后，插值得到的。第4列和第5列分别是MFlow软件使用六面体和混合网格预测的阻力，从图可以发现，MFlow的结果位于两个风洞试验结果的区间内，而且与计算的平均值很接近，特别是六面体网格结果。这也证明了程序在翼身组合体外形阻力预测方面有着可靠的计算精度。

图8 阻力系数的网格收敛性Fig.8 Grid convergence characteristics of drag coefficients

图9 AIAA第5届阻力预测研讨会CRM阻力预测结果比较[26]Fig.9 Results comparison of drag prediction with CRM in the 5th AIAA Drag Prediction Workshop [26]

5 结 论

1) 通过改进传统Green-Gauss梯度求解方法，发展了节点型Green-Gauss方法，克服了现有梯度求解方法的缺陷，更好地模拟了梯度变化剧烈区域的压力分布特征，提高了数值方法的鲁棒性和阻力预测精度。

2) 通过对NASA通用研究模型的数值模拟，以及网格收敛性和数据对比分析，进一步考核和验证了软件的计算精度和可靠性。

[1] 阎超, 席柯, 袁武, 等. DPW系列会议评述与思考[J]. 力学进展, 2011, 41(6): 776-784.

YAN C, XI K, YUAN W, et al. Review of the drag prediction workshop series[J]. Advances in Mechanics, 2011, 41(6): 776-784 (in Chinese).

[2] LEVY D W, ZICKUHR T, VASSBERG J C, et al. Summary of data from the first AIAA CFD drag prediction workshop: AIAA-2002-0841[R]. Reston，VA: AIAA, 2002.

[3] LAFLIN K R, KLAUSMEYER S M, ZICKUHR T, et al. Summary of the second AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2005, 42(5): 1165-1178.

[4] VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the third AIAA CFD drag prediction workshop[J]. Journal of Aircraft, 2008, 45(3): 781-798.

[5] VASSBERG J C, TINOCO E N, MANI M, et al. Summary of the fourth AIAA CFD drag prediction workshop: AIAA-2010-4547[R]. Reston，VA: AIAA, 2010.

[6] SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences: NASA/CR-2014-218178[R]. Washington, D. C.: NASA， 2014.

[7] BARTH T J. An overview of combined uncertainty and a posteriori error bound estimates for CFD calculations: AIAA-2016-1062[R]. Reston，VA: AIAA, 2016.

[8] 王运涛, 孟德虹, 孙岩, 等. DLR-F6/FX2B翼身组合体构型高精度数值模拟[J]. 航空学报, 2016, 37(2): 484-490.

WANG Y T, MENG D H, SUN Y, et al. High-order accuracy numerical simulation of DLR-F6/FX2B wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 484-490 (in Chinese).

[9] JOHNSON F T, TINOCO E N, YU N J. Thirty years of development and application of CFD at Boeing Commercial Airplanes, Seattle[J]. Computer and Fluid, 2005, 34(10): 1115-1151.

[10] 张健, 邓有奇, 李彬, 等. 一种适用于三维混合网格的GMRES加速收敛新方法[J]. 航空学报, 2016, 37(11): 3226-3235.

ZHANG J, DENG Y Q, LI B, et al. A new method to accelerate GMRES’s convergence applying to three-dimensional hybrid grid[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3226-3235 (in Chinese).

[11] 徐嘉, 刘秋洪, 蔡晋生, 等. 基于隐式嵌套重叠网格技术的阻力预测[J]. 航空学报, 2013, 34(2): 208-217.

XU J, LIU Q H, CAI J S, et al. Drag prediction based on overset grids with implicit hole cutting technique[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 208-217 (in Chinese).

[12] 王运涛, 李松, 孟德虹, 等. 梯形翼高升力构型的数值模拟技术[J]. 航空学报, 2014, 35(12): 3213-3221.

WANG Y T, LI S, MENG D H, et al. Numerical simulation technology of high lift trapezoidal wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3213-3221 (in Chinese).

[13] 康忠良, 阎超. 适用于混合网格的约束最小二乘重构方法[J]. 航空学报, 2012, 33(9): 1598-1605.

KANG Z L, YAN C. Constrained least-squares reconstruction method for mixed grids[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1598-1605 (in Chinese).

[14] LEVY D W, CHAN M S. Comparison of viscous grid layer growth rate of unstructured grids on CFD drag prediction workshop results: AIAA-2010-4671[R]. Reston，VA: AIAA, 2010.

[15] MAVRIPLIS D J. Viscous flow analysis using a parallel unstructured multigrid solver[J]. AIAA Journal, 2000, 38(11): 2067-2076.

[16] ALLMARAS S R, BUSSOLETTI J E. Algorithm issues and challenges associated with the development of robust CFD codes[R]. New York: Springer, 2009: 1-19.

[17] TINOCO E N, BOGUE D R, KAO T J, et al. Progress toward CFD for full flight envelope[J]. The Aeronautical Journal, 2005, 109(1100): 451-460.

[18] EMRE S, CHRISTOPH B. Gradient calculation methods on arbitrary polyhedral unstructured meshes for cell-centered CFD solvers: AIAA-2014-1440[R]. Reston,VA: AIAA, 2014.

[19] SHIMA E, KITAMURA K, HAGA T. Green-Gauss/weighted-least-squares hybrid gradient reconstruction for arbitrary polyhedral unstructured grids[J]. AIAA Journal, 2013, 51(11): 2740-2747.

[20] ANDREW W C, ANDREW J D. Towards accurate flow predictions using unstructured meshes:AIAA-2009-3650[R]. Reston, VA: AIAA, 2009.

[21] 张耀冰. 运输机气动特性混合网格数值模拟研究[D]. 绵阳：中国空气动力研究与发展中心， 2014.

ZHANG Y B. Numerical simulation of transport aircraft’s aerodynamic characteristics using mixed grid[D]. Mianyang：China Aerodynamics Research and Development Center， 2014 (in Chinese).

[22] BLAZEK J. Computational fluid dynamics: Principles and applications[M]. Oxford: Elsevier Science Ltd.， 2001：129-179.

[23] SAXENA S K, MANOJ T N. Implementation and testing of Spalart Allmaras model in a multi-block code: AIAA-2002-0835[R]. Reston,VA: AIAA, 2002.

[24] REDEKER G. DLR-F4 wing body configuration, in Chapter B of a selection of experimental test cases for the validation of CFD codes: AGARD-1994-AR-303[R]. Paris: AGARD, 1994.

[25] SHAHYAR Z P, NEAL T F. Assessment of the unstructured grid software TetrUSS for drag prediction of the DLR-F4 configuration: AIAA-2002-0839[R]. Reston,VA: AIAA, 2002.

[26] TINOCO E, LEVY D. DWP 5 summary of participant da-ta[C]∥5th CFD Drag Prediction Workshop. Reston, VA: AIAA, 2012.

[27] 李钊, 陈海昕, 张宇飞. 基于广义Richardson外插方法的阻力预测精度分析[J]. 航空学报, 2015, 36(7): 2105-2114.

LI Z, CHEN H X, ZHANG Y F. Accuracy analysis of drag prediction based on generalized Richardson extrapolation[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2105-2114 (in Chinese).