单桩荷载—沉降关系的解析算法

马晨光 崔广芹

(1.内蒙古寅岗建设集团有限公司，内蒙古 包头 014010； 2.内蒙古科技大学土木工程学院，内蒙古 包头 014010)

1 概述

单桩刚度不仅受桩体自身材料、几何尺寸等的影响，而且与桩侧土、桩端土的力学特性密切相关。本文首先在考虑桩土界面应力—应变非线性及桩土滑移的基础上建立了桩土荷载传递模型，然后基于桩身整体平衡关系和边界条件、采用荷载传递法分析并推导了不同桩顶荷载下桩身的荷载—沉降和单桩刚度表达式。

2 桩土荷载传递模型的建立

2.1 单桩沉降计算理论

本文将基于荷载传递法进行单桩沉降计算及推导桩身荷载—沉降关系。此方法概念明确，只要选用合理的传递函数模型，就可以考虑桩周土的非线性及桩土滑移特性，并易得到桩身荷载—沉降关系的解析解。

文献[1]推导了桩土荷载传递的基本微分方程及Q(z),τ(z),S(z)之间的关系：

(1)

(2)

(3)

其中，S(z)为z深度处桩身总位移(包括桩身压缩变形和桩端土层的压缩导致的桩身位移)；U，A，E分别为桩身周长、截面面积和桩体材料的弹性模量；τ(z)，Q(z)分别为z深度处桩侧摩阻力及桩身轴力的大小。

求解式(1)的关键是确定合理的桩土荷载传递函数模型(桩侧土的τ—s关系模型)。

2.2 荷载传递模型的建立

Seed和Reese(1957)利用现场十字板剪切试验测得土体抗剪强度和扭转位移之间近似呈双曲线关系，并以此作为桩土荷载传递函数；Coyle和Reese(1966)经室内模型桩三轴试验发现桩侧土表现出一定的软化特性。文献[1]中提出了一些传递函数模型和微分方程的求解方法，以Kraft(1981)的双曲线模型最为常用，后期又出现折线简化模型，如陈龙珠的双折线弹塑性硬化模型，房卫民的三折线模型等等。研究表明，桩端土压应力—应变也呈现非线性特性，且桩端土一般所处土层较好，多呈现应变硬化特性。

上述模型中，折线模型可以模拟桩侧土的非线性特性，且比双曲线模型的计算量小，可以考虑桩土滑移现象，容易推求各阶段的解析解，又可以通过变换直线段的斜率来模拟桩侧土的剪切应变软化特性，这些是双曲线模型所不能实现的。

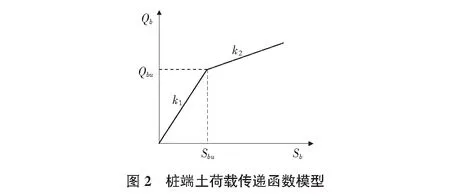
本文采用三折线模型(如图1所示)模拟桩侧土荷载传递性状，采用双折线硬化模型(如图2所示)模拟桩端荷载及位移(Qb—Sb)的关系。

桩侧土传递函数表达式为：

(4)

其中，Su1,Su2均为界限位移；τu1为Su1对应的桩侧摩阻力；τu为极限侧阻；λ1,λ2均为抗剪刚度系数，kPa/mm，λ2>0时，表示非线性弹塑性模型，λ2=0时，表示理想弹塑性模型，λ2<0时，表示软化模型。

桩端土传递函数表达式为：

(5)

其中，Sbu为界限位移；k1,k2分别为桩端土处于界限位移Sbu前、后的抗压刚度系数，kN/mm。

本文在计算过程中作如下假定：

1)桩身变形为线弹性的；

2)桩侧土为均质，沿桩身不变，对于分层土可取加权平均值，τ—s曲线斜率沿桩长不变；

3)不考虑负摩阻力、桩端沉渣的影响，不考虑侧阻对桩端沉降的影响。

3 单桩荷载—沉降关系解析解

3.1 桩端无位移—桩侧土部分处于弹性状态[2]

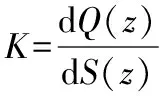
(6)

根据式(2),式(3),式(6)及式(4)第一式化简得:

则，此状态下桩身刚度为一常数。

(7)

桩顶荷载—沉降关系为:

(8)

可见，此阶段单桩刚度为常数，只与桩身物理参数及桩侧土模型参数λ1有关。

3.2 桩端有位移—桩侧土全部处于弹性状态

侧阻τ(z)=λ1S(z)，由式(1),式(4)第一式及边界条件：

化简得z=0处，桩顶沉降和桩顶荷载表达式为:

(9)

1)由式(9)，式(5)第一式得桩端土为弹性状态时的单桩刚度表达式和桩顶荷载—沉降关系表达式分别为：

(10)

Q0=Kee·S0

(11)

2)由式(9)，式(5)第二式得桩端土处于硬化状态时对应表达式分别为:

(12)

Q0=Kep·S0

(13)

由式(9)可得，桩端位移Sb=Sbu时，对应的桩顶沉降S0cr为：

当S0≤S0cr时，按式(10)计算单桩刚度；当S0cr

可见，此阶段单桩刚度Kee,Kep皆为常数，与桩身物理参数及模型参数λ1,k1或k2有关。

3.3 桩侧土部分处于弹塑性状态

桩身上部(AC段)土体进入弹塑性状态，长度记为L2；下部(CD段)土体仍处于弹性阶段，长度记为L1。C截面处满足位移、应力协调条件，截面位移SC、轴力QC按照弹性阶段计算。通过式(1),式(4)第二式及C截面边界条件[3]:

1)当桩端土处于弹性状态时，对应表达式分别为：

(14)

Q0=KpeS0+Rλγ22Su1-KpeRλ(χ22-1)Su1

(15)

2)当桩端土处于硬化状态时，对应表达式分别为:

(16)

(17)

可见，此阶段单桩刚度随弹塑性段长度L2的变化而不同，当L2=0时，式(14)，式(16)分别与式(10)，式(12)一致。

3.4 桩侧土部分处于塑性滑移状态

桩身AB段土体进入塑性滑移状态，侧阻均匀分布，大小为τu。AB,BC,CD段长度分别为L3,L2,L1(满足：L1+L2+L3=L)。B截面处满足位移、应力协调条件，截面位移SB、轴力QB按照第三阶段下桩顶沉降、荷载的计算方法求解。由式(1),式(4)第三式及B截面边界条件可得：

1)桩端土处于弹性状态时，单桩刚度及桩顶荷载—沉降关系解析表达式为：

(18)

(19)

2)桩端土处于硬化状态时，可得:

(20)

(21)

可见，此阶段的单桩刚度随L1,L2,L3的变化而不同，当L3=0时，式(18)，式(20)分别与式(14)，式(16)一致。

3.5 桩侧土全部处于塑性滑移状态

此时桩端土位移已较大，已进入应变硬化状态，将L3=L，L2=0，L1=0分别代入式(20),式(21)即可得到此时单桩刚度和桩顶荷载—沉降关系的解析表达式:

(22)

(23)

此阶段单桩刚度为常数，与桩身物理参数及桩端土模型参数k2有关。

式(7)，式(8)，式(10)～式(23)即为不同桩顶荷载水平下单桩刚度及桩顶荷载—沉降关系的解析表达式，且不同阶段的单桩刚度与不同的模型参数有关，式中各参数具有一定规律，易于编程。

现场单桩静载荷试验得到的Q—S曲线反映了不同荷载下桩顶荷载—沉降关系的变化特征，若将本文所求单桩刚度及桩顶荷载—沉降关系解析表达式同现场单桩Q—S曲线结果相结合，建立二者的对应关系，再配合静力触探等其他现场原位试验，即可由实测曲线结果反算出相应的传递模型参数，为进一步的桩基计算奠定基础。

4 结语

本文以荷载传递法作为单桩沉降计算的基本理论，对桩侧土和桩端土分别采用三折线模型和双折线硬化模型，同时考虑了侧阻与桩身位移、端阻与桩端位移的非线性关系、桩土滑移及桩侧土应变软化特性。

按照桩顶荷载增加过程中桩土荷载的传递特性，将桩周土所处状态划分为五个发展阶段。然后，基于桩身整体平衡关系和边界条件，分析并推导了不同荷载工况所对应的单桩刚度及桩顶荷载—沉降关系的解析表达式。

解析式可以反映单桩刚度与各传递模型参数之间的关系，通过将其与现场单桩静载荷试验的Q—S曲线资料相结合，并配合其他相关原位试验即可反算出相应的模型参数，为进一步的桩基计算奠定基础。

[1] 《桩基工程手册》编写委员会.桩基工程手册[M].北京:中国建筑工业出版社,1995.

[2] 曹汉志.桩的轴向荷载传递及荷载—沉降的数值计算方法[J].岩土工程学报,1986,8(6):37-49.

[3] 刘 杰,张可能,肖宏彬.考虑桩侧土软化时单桩荷载—沉降关系的解析算法[J].中国公路学报,2003,16(2):61-64.