找准核心问题，发展抽象思维

王玉彬

【摘 要】数学课堂教学中，培养学生的抽象思维是基本目标之一。因此，教师要根据教学目标，找准核心问题，克服过多过小的问题和活动，给学生留足思考的空间，让学生在解决问题的过程中观察、分析、思考、探索、交流，发现数学的本质，从而发展学生的抽象思维。

【关键词】小学数学；核心问题；教学

抽象是数学的思想方法之一，东北师范大学史宁中教授说：“数学教育的终极目标是，一个人学习数学之后，即便这个人未来从事的工作和数学无关，也应当会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界。”1如何在课堂教学中发展学生的抽象思维，这是数学教师应该关心的问题。

【教学案例】

六年级“正比例的意义”的教学，需要关注两个量的变化，对学生来说非常抽象，有的教师设计了两个情境。

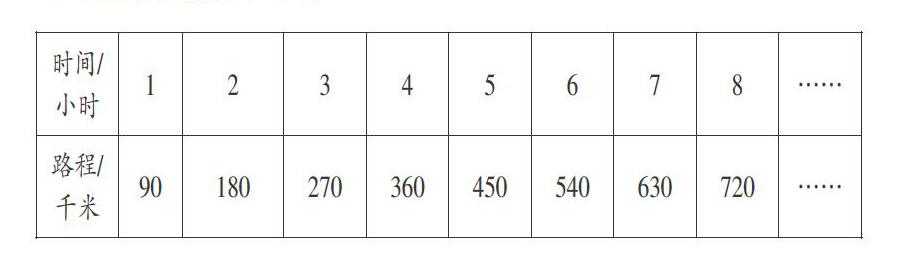
1.通过“汽车匀速行驶时，路程随时间的变化”让学生观察和思考：什么在变？什么没变？初步感知“正比例的意义”。

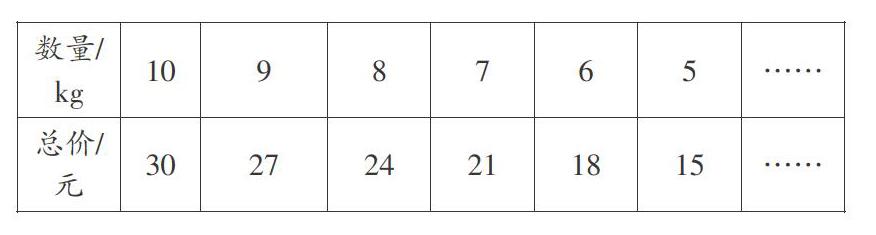
2.通过“买某种苹果时，总价和数量的变化”，进一步思考“什么在变？什么没变？”再次感知正比例的意义。

学生在行程问题中能说出“路程和时间在变，速度没变”，但总结不出“路程与时间对应的数的比值不变”；他们会说买苹果时“单价不变”，但却始终不能说出“总价和单价对应的数的比值不变”。因为在孤立单一的情境中，学生不会把“变化”当作思考对象，很难发现呈正比例的两个量的变化有什么共同特征。

教师用两个情境进行的“小步子”教学，让学生抽象出呈正比例的两个量的变化特征，看似降低难度，实际上， 学生每次看到的都是一种变化。没有比较，没有归类，学生难以从众多的变化中抽象出“呈正比例的两个量”的变化特征。而且课堂上，教师留给学生探究、思考的空间很小，不利于学生数学思维的培养。

【教学思考】

那么如何设计学习活动，才能激发学生观察思考、自己总结出呈正比例的量的特征，培养学生的抽象思维呢？

一、针对教学目标，找准核心问题

（一）核心问题要直指教学目标

根据教学目标以及学生已有的知识经验，找到本节课的知识生长点，准确定位要解决的核心问题。例如“正比例的意义”这节课，教学目标如下表：

[1.通过生活中的实例，发现生活中两个相关联的量，认识呈正比例关系的量，能根据正比例的意义判断两种量是否呈正比例关系。

2.通过自主探索，进一步培养学生观察、分析、推理等能力。

3.初步感悟渗透函数思想。]

综合看这节课的教学目标，可以看出本节课要解决的核心问题是“呈正比例的两个量有什么特征？”

（二）核心问题要有挑战性

平时教学中，总能发现，问题一提出，几乎全班学生都举手发言，看似流畅，实则说明问题的难度太低，学生思考的空间很小。课堂上为了促进学生深度思考，教师要提出对学生有挑战性的问题。北京市特级教师张红，在一次讲座中提到教师要善于提出“胖”问题，也就是能够引起学生发散思维和深度思考的问题。针对“正比例的意义”这节课，核心问题是找到“呈正比例的两个量”有什么特征。这是个大问题，需要学生综合分析变化情境，通过分析归类，不断抽丝剥茧，才能抽象出“正比例”的内涵。所以这个问题是一个有深度、对学生来说有挑战的问题，能引起学生的深度思考。

二、根据核心问题，设计核心活动

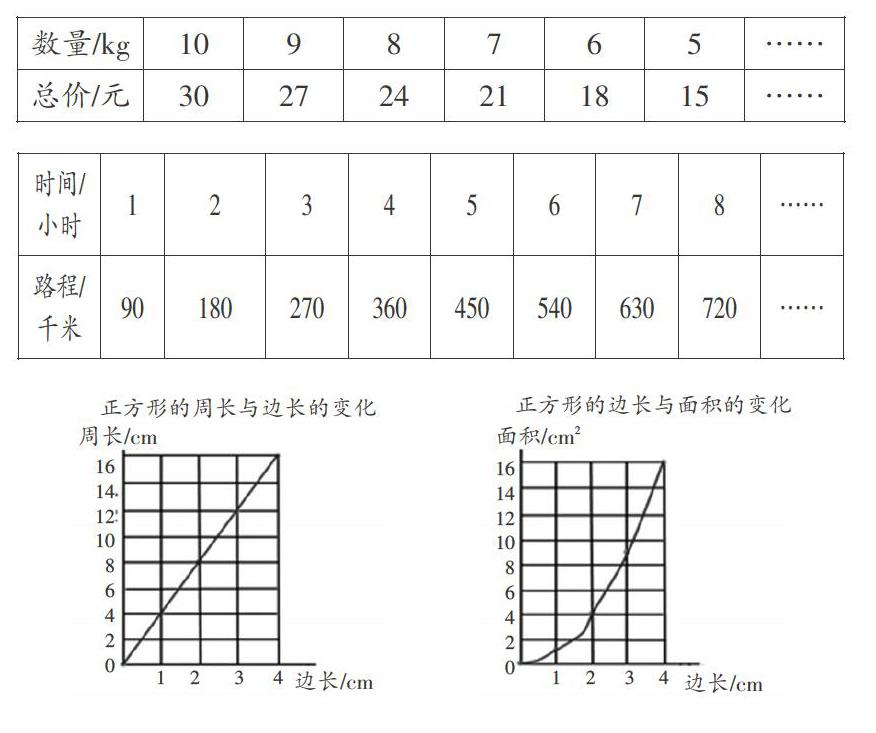
核心活动，就是能解决核心问题的学习活动。这个活动要有一定的整合性、趣味性和真实性。例如在“正比例的意义”的改进教学中，可以给学生设计这样的一个活动：小组合作，观察下面的4个图表，你发现它们有什么共同点和不同点？

这个问题比较难回答，需要学生深入思考，在小组充分思考后，进行全班交流。

生1：共同点是每个表、图中的两个量都在变化。路程随着时间在变化……

教师补充：一个量随着另一个量的变化而变化，这两个量就是相关联的量。

生2：我发现正方形的周长随边长变化的图是一条直线。

师：为什么是直线？

生4：变化是“均匀”的，边长每增加1厘米， 周长就增加4厘米。

师：不均匀变化的是谁？能举个例子吗？

生3：正方形的面积。边长1厘米，面积1平方厘米；边长增加到2厘米，面积为4平方厘米，增加了3平方厘米；如果边长再增加1厘米，面积为9厘米，增加了5厘米。你看，边长每增加1厘米，但是面积增加的却不一样。

师：你说的“均匀”变化太形象了，找一找，还有哪些实例是这样均匀变化的？

其他学生陆续举手发言，举例说明，汽车匀速行驶时路程随时间的变化，购买苹果时总价随着数量的变化，都是匀速变化。

所有学生为自己的发现而自豪，教师引导他们思考：为什么它们能“均匀”变化呢？

他们开始关注图中不变的那个量，然后学生自然地发现两个量的对应的数的比值是不变的，从而对正比例的内涵有更深的领悟。在这个整合之后的大的活动之下，学生充分思考，在交流中相互启发，一个问题生发另一个问题，不断地朝着学习目标越走越近，抽象思维得到一定的发展。

三、核心活动的节奏要慢下来

一节课40分钟，如何在有限的时间内，让学生在知识、方法、能力上获得更多，这是每一位教师要思考的问题。平时总能看到一些教师的课堂节奏很快，一个情境接着一个情境，一节课完成的任务貌似很多，但实际上只是蜻蜓点水、走马观花，不能引发学生深层次的思考。课堂上教师要学会慢下来。北京市特級教师刘延革说，课堂上她提出问题后，不希望一下子有很多学生举手，而是经过一两分钟的思考后，三三两两的学生举手，然后更多的学生举手发言，最后经过争辩和讨论，每一个学生都能在原有的思维层次上有所提升，这才是高效的课堂。对于挑战性的问题学生需要思考的时间，教师要学会等待，不要急于展现热闹的课堂。

总之，教师要抓住数学知识的本质，紧紧围绕教学目标，在教学活动中，给学生深入思考的时间和空间。只有让学生自己去经历这样的“思维历练”，在每堂课的学习中落实学生数学核心素养的培养，才能真正发展学生的抽象思维。

（北京市房山区教师进修学校 102488）