独柱墩连续箱梁桥的抗倾覆稳定性分析

(永州市交通建设投资有限公司，湖南 永州 425000)

随着我国城市基础建设的快速发展，城市立交桥和高架桥的结构形式越来越多样化[1]。为提升立该结构型桥梁的适地性与行车舒适性，独柱墩连续梁桥得到广泛应用[2,3]。因独柱墩桥梁的支撑方式为单点支撑，当遇到严重超载情况时，桥梁会出现倾覆破坏[4,5]。近年来，国内发生多起由于严重超载导致独柱墩桥倾覆倒塌事故，造成巨大经济损失和人员伤亡[6]。目前，我国桥梁设计者大多仅考虑了桥梁的抗弯、抗剪性是否符合规范要求[7,8]，而桥梁抗倾覆稳定性的安全储备没有足够重视。基于此，本文基于MIDAS Civil有限元软件，分别对4种不同车道荷载形式下的独柱墩连续箱梁桥进行抗倾覆稳定性研究，分析结果可为独柱墩连续梁桥的抗倾覆设计提供理论依据。

1 工程概况

依托某高架桥左幅第3联为背景，其上部结构为5×23.08 m的预应力混凝土连续箱梁，下部结构采用独柱墩、承台接灌注桩基础。该桥为单箱4室箱梁，采用满堂支架现浇施工，主梁高度为1.5 m，顶板和底板宽度分别为13.5、6.3 m。桥梁设计荷载等级为公路-Ⅰ级。桥梁总体布置如图1所示。

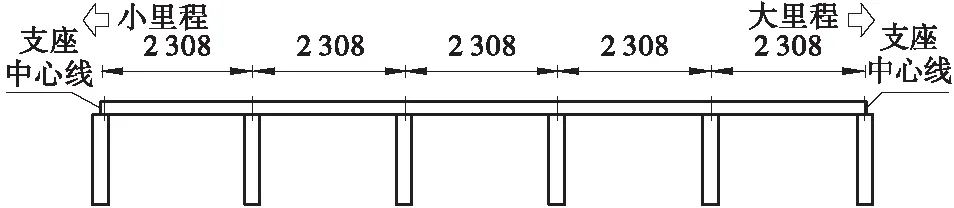
图1 桥梁布置图(单位： cm)

2 建立模型

考虑到独柱墩连续箱梁桥的构造特点及计算精度要求，运用MIDAS Civil有限元软件，采用梁单元法建立全桥计算模型，针对不同荷载下预应力混凝土连续梁桥进行抗倾覆稳定性分析。全桥模型如图2所示，模型中支座本身采用弹性连接方式，支座与主梁和墩顶的连接方式分别采用刚性连接、固结模拟，整个模型中共265个节点，230个单元，模型坐标系中X、Y、Z分别表示桥梁的纵向、横向、竖向。全桥支座布置情况如图3所示，其中支座1～6号为双向支座，7、8号及10～12为单向支座，9号为固定支座。

图2 全桥有限元模型

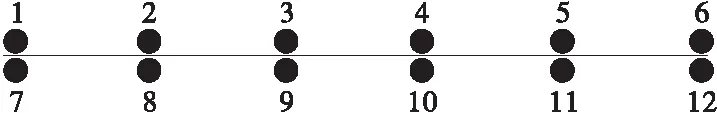
图3 支座编号

模型分析过程中主要考虑了混凝土收缩和徐变、结构自重、汽车荷载、基础变位、整体温度、预应力以及温度梯度的作用。其中二期荷载取40 kN/m，基础变位0.008 m；系统温度考虑整体升降温均为20 ℃；温度梯度考虑正温差T1=14 ℃，T2=5.5 ℃；反温差T1=-7 ℃，T2=-2.75 ℃，各项取值均满足规范要求。依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62—2012中规程分别确定主梁材料C40混凝土的收缩及徐变系数，其函数曲线如图4所示。

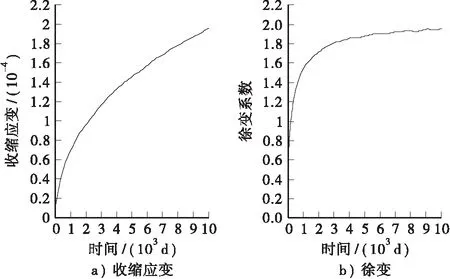
图4 混凝土的收缩应变及徐变系数

目前，国内在桥梁抗倾覆稳定性方面的研究还处于发展阶段，因此抗倾覆稳定的规范尚不成熟，由于桥梁超载现象较为严重，其抗倾覆稳定性验算仅采用公路—Ⅰ级荷载可能会导致结果存在偏差。基于此，本文综合考虑了《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62—2012、《桥梁上部结构抗倾覆验算荷载的规定》和《公路桥涵设计通用规范》JTG D60—2015等规范中提及的车载形式，拟定4种不同车道荷载条件，针对该高架桥抗倾覆稳定性展开系统分析。各车道荷载情况如表1所示。

表1 拟定车道荷载情况序号荷载形式实际情况序号荷载形式实际情况1公路-Ⅰ级标准355t重车重度超载21 3倍公路-Ⅰ级一般超载43倍公路-Ⅰ级严重超载

在模拟分析过程中为保证各车道荷载作用下主梁能够发生最大程度的横向倾覆效应，参考桥梁倾覆损害的荷载特征，将4种不同荷载均布置于该桥梁单向3车道的最外侧车道，具体车载布置情况如图5所示。桥梁重要性系数和车辆活载冲击系数分别取1.0、1.26，依据《公路桥涵设计通用规范》JTG D60—2015中相关规定，将各作用效应组合成4种不同工况，并对其进行抗倾覆稳定性分析，具体工况如表2所示。

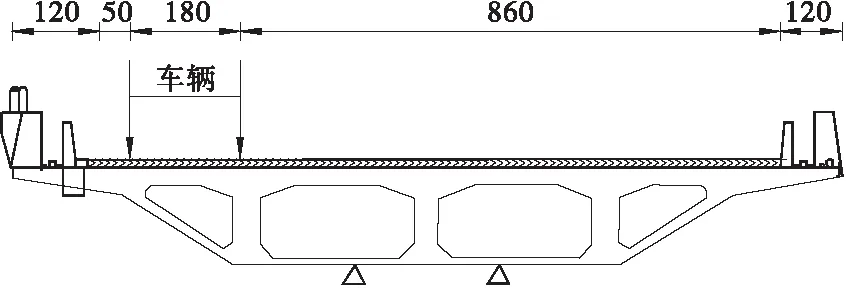
图5 车辆荷载布置示意(单位： cm)

表2 模拟组合工况工况永久作用汽车荷载(计冲击)全桥整体升温全桥整体降温工况1正温差工况2反温差工况3正温差工况4反温差

3 抗倾覆稳定性分析

3.1 倾覆轴线的确定

当桥梁受到较大车载偏载作用时，其边界条件会因支座的脱空而失效，造成桥梁整体失衡发生倾覆破坏。研究桥梁抗倾覆稳定性时，首先需要确定倾覆轴线，由于模拟试验中的桥梁属于直线梁式桥，且中墩和边墩两者的支点间距相等，因此该桥的倾覆轴线为车辆荷载作用在侧支座的连线，其倾覆轴线如图6所示。

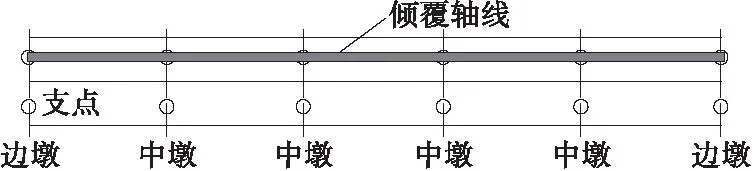
图6 桥梁倾覆轴线示意

3.2 不同车载条件下抗倾覆稳定性分析

通过对不同车道荷载作用下的模拟桥梁进行抗倾覆稳定性数值分析，得出最大倾覆效应时各支座的反力，并依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62—2012中相关规定，采用下述公式计算出桥梁的抗倾覆稳定系数。

(1)

式中：kqf表示抗倾覆稳定系数；RGi表示成桥时各支座反力；xi表示各支座至倾覆轴线的垂直长度；μ表示冲击系数；qk和pk分别表示车道荷载中均布、集中荷载；l表示桥梁整体长度；e表示横向最不利车道处至倾覆轴线的垂直长度。计算过程中各参数如表3所示，不同荷载作用下桥梁支座反力的变化曲线如图7所示，抗倾覆稳定系数变化曲线如图8所示。

表3 计算参数冲击系数1+μ桥梁全长l/m车道至倾覆轴距离e/m支座至倾覆轴距离x/m1．26115．352．772．34

图7 不同荷载作用下支座反力变化曲线

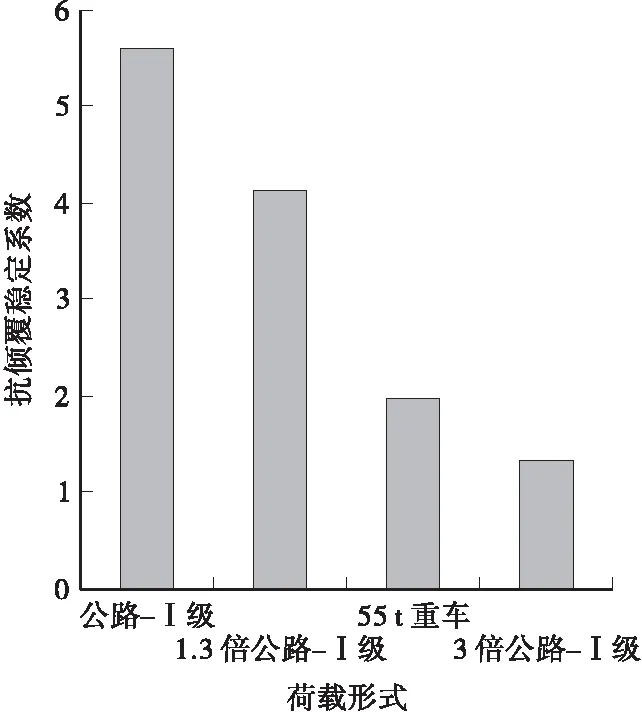
图8 抗倾覆稳定系数变化曲线

从图7中可看出，在不同车道荷载形式及工况情形下，桥梁的各支座均没有发生脱空现象，表明符合《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62—2012和《公路桥涵设计通用规范》JTG D60—2015相关规定。由不同荷载形式下各工况支座反力数据可知，工况1、3的支座反力基本相同，而工况2、4的支座反力也大致相似，表明整体升降温不会对支座反力产生明显影响；工况1、2中相同位置的支座反力约差39 kN，表明温度梯度能够对支座反力产生较大影响。另外，相同车辆荷载形式下不同工况的横向抗倾覆系数均一致。

由图7可知，当桥梁受到车载偏载作用时，各工况支座反力的变化曲线均基本相似，其中桥梁两端的支座反力值最小，而跨中处的反力值最大，支座反力的变化趋势均沿边墩至跨中逐渐上升。根据整个桥梁的支座反力变化曲线可知，车载作用的一侧较于另一侧明显要大，同时也可表明该类型桥梁的边支座较于其他支座更具脱空破坏风险，因此在设计独柱支承的连续梁桥时应着重注意。根据图8可知，桥梁的抗倾覆系数随着车辆荷载的增大逐渐减小，使得其抗倾覆稳定性也随之下降。

不同车道荷载形式下桥梁产生的荷载如表4所示。根据表中数据可知，该独柱墩连续箱梁桥在公路—Ⅰ级(即标准设计荷载)作用下产生的荷载为1463.6 kN；在1.3倍公路—Ⅰ级车辆荷载作用下产生荷载达1902.6 kN，同时说明该桥超载30%。而在桥梁实际运营中经常出现55 t重车荷载情况，其产生荷载约为1.3倍公路—Ⅰ级车辆荷载的1倍，因此针对独柱墩连续箱梁桥进行抗倾覆稳定性验算时，以公路—Ⅰ级和1.3倍公路—Ⅰ级为验算荷载显然无法满足安全要求，但使用更重形式的荷载来验算时，易造成实际桥梁的造价过高、结构过于保守等问题。综合上述分析可知，在独柱墩连续箱梁桥车道荷载的验算过程中，应结合桥梁的交通实况，适当提高验算车辆的总荷载，并基于可靠度理论确定抗倾覆稳定性的安全储备限值，从而确保实际运营中梁式桥具有更加良好的安全性和经济性。

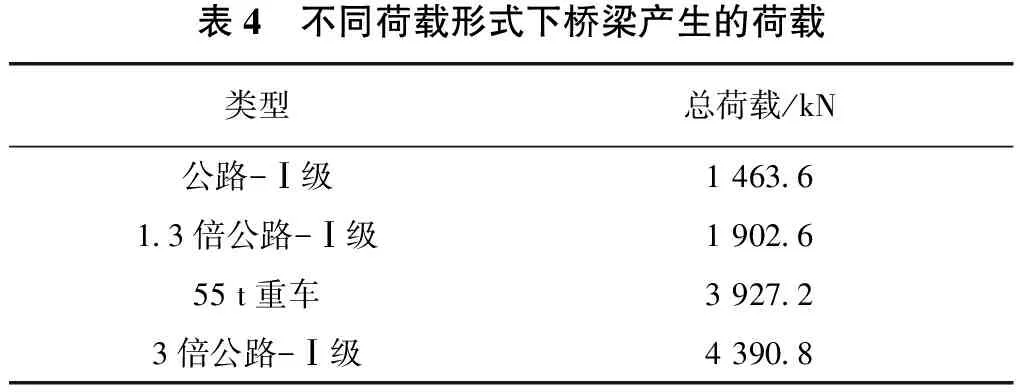
表4 不同荷载形式下桥梁产生的荷载类型总荷载/kN公路-Ⅰ级1463 61 3倍公路-Ⅰ级1902 655t重车3927 23倍公路-Ⅰ级4390 8

4 结论

1) 相同车辆荷载形式下不同工况的横向抗倾覆系数均一致；整体升降温不会对支座反力产生明显影响，而温度梯度能够对支座反力产生一定影响；桥梁的抗倾覆系数随着车辆荷载的增大逐渐减小，使得其抗倾覆稳定性也随之下降。

2) 在独柱墩连续箱梁桥车道荷载的验算时，应综合考虑桥梁的交通实况，适当提高验算车辆的总荷载，并基于可靠度理论确定出抗倾覆稳定性的安全储备限值，以确保实际运营中梁式桥具有更加良好的安全性和经济性。

[1] 刘飞，刘世忠，张慧，等.独柱曲线刚构匝道桥抗倾覆稳定试验研究[J].兰州交通大学学报，2012(4)：26-30.

[2] 周列茅.独柱支墩连续箱梁桥的倾覆事故成因分析[J].公路交通科技(应用技术版)，2011(7)：179-181.

[3] 吴玉华，蔡若红，杨育人.独柱墩连续梁桥的稳定影响因素分析[J].公路工程，2011(6)：93-96.

[4] 李盼到，张京，王美.独柱支承梁式桥倾覆稳定性验算方法研究[J].世界桥梁，2012(6)：52-56.

[5] Arizumi Y，Hamada S，Oshiro T.Behavior study of curved composite box girders[J].Journal of Structural Engineering，2014，114(11):2555-2573.

[6] 庄冬利.偏载作用下箱梁桥抗倾覆稳定问题的探讨[J].桥梁建设，2014，44(2):27-31.

[7] 王伟.独柱墩曲线梁桥抗倾覆性能的研究[D].重庆:重庆交通大学,2014.

[8] 姜爱国，杨志.独柱墩曲线梁桥倾覆轴线研究[J].世界桥梁，2013(4)：58-61.