2017年高考数学全国Ⅰ卷压轴题的研究与反思

☉华中师范大学数学与统计学学院 吴洁莹

☉华中师范大学数学与统计学学院 徐章韬

一、试题再现

题目已知函数f（x）=ae2x+（a-2）ex-x.

（1）讨论f（x）的单调性；

（2）若f（x）有两个零点，求a的取值范围.

这道试题是2017年高考全国新课标Ⅰ理科卷的21题.考查的内容是函数单调性与零点的知识，这些知识是学生在高考复习中已经非常熟练掌握的.求解这道试题的思路，学生也已基本掌握，关键就在于计算能力与转换思维.

二、试题分析

1.第（1）问的分析

第（1）问是对含参数的函数进行求导，分析函数单调性.这样简单的函数求导问题对学生来说没有难度.导数f′（x）=2ae2x+（a-2）ex-1，要判断函数单调性即要判断f′（x）=2ae2x+（a-2）ex-1的符号正负，一般情况下先令导数为0.此时，对于基础一般的学生来说，求解极值点会比较困难，他们难发现可将ex当作整体，将原导函数方程转化为f′（x）=2a（ex）2+（a-2）ex-1，导数为0时这是一个关于ex的一元二次方程，即f′（x）=2a（ex）2+（a-2）ex-1=（2ex+1）（aex-1）=0.当a≤0时，方程无解，f′（x）＜0；当a＞

综上：当a≤0时，f（x）在R上单调递减；当a＞0时，f（x）

第（1）问学生的解答难点在于对导函数形式转换以及对参数a的分类讨论，若能将导函数进行因式分解，之后对参数a的分类讨论也将不再是难点.在学生已有的知识基础上，简单二次函数的因式分解不是问题，然而高考数学压轴题的考查总是源于教材又高于教材.经笔者对历年高考题和各省市近几年函数压轴题的统计发现，一般函数的压轴题第一问都是判断函数单调性，有时含参有时不含参，但不论是怎样的单调性分析，大部分都要考查学生对复杂函数进行因式分解的能力（也可称为运算能力），进而判断函数单调性.对复杂函数进行因式分解在高考中已经是不可缺少的能力.

2.第（2）问的分析

在已知函数f（x）=ae2x+（a-2）ex-x有两个零点时，求参数a的取值范围.求解这一问一般有两个思路，思路1：利用函数图形判断函数零点；思路2：转化函数.下文将从这两个思路对此试题进行分析.

思路1分析：由第（1）问中对函数单调性的判断，可画出函数图形，判断在哪种情况下函数图像与x轴有两个不同的交点.显然，当a≤0时，f（x）在R上单调递减，此时函数不可能有两个零点，故a≤0不成立；当a＞0时，f（x）画出函数简图，如图1.

图1

图2

（f-1）=ae2x-1+（a-2）e-1-（-1）=，故可

思路2分析：函数（fx）=ae2x+（a-2）ex-x有两个零点，求参数a的参数范围.这个思路也很明显，学生能快速想到，直接令（fx）=0，则a=，得到a关于x的方程，由于（fx）=0有两个解，不妨设这两个解分别为x1，x2，其中x1＜.接下来就

可以从几个角度去分析参数a的参数范围.

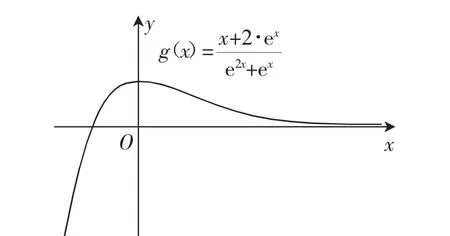
图3

由图像明显可以看出，0＜a＜1.

从角度1分析，这也是学生在高考复习中已经练习过的内容，分离参数，两函数的交点个数即是原函数的零点个数，学生处理的难点在于分离参数的过程及对参数方程的单调性判断，这个函数求导具有一定的难度，判断单调性需要学生有较强的运算能力与观察能力.

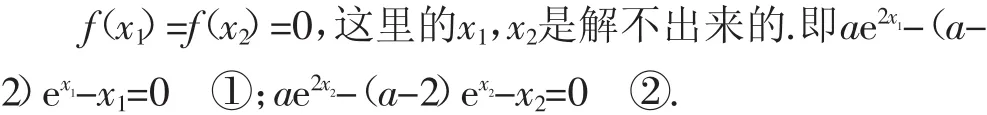
角度2：利用放缩法，先猜后证.

①式-②式得a（ex1-ex2）（ex1+ex2+1）=x1-x2+2（ex1-ex2），所为函数y=ex上两点斜率的导数且恒大于0，故当函数有两个零点时a＞0.接下来要讨论的就是当制.一般想法是通过x1，x2的限制，利用不等式知识求解a的取值范围，但x1，x2之间到底具有怎样的关系还不明确.此时考虑当x→0时，a→1；当x→+∞时，a→0，故可猜测a＜1.由泰勒展开式

从角度2分析，前半部分函数有两个零点，得到①、②两式，基本都能想到，甚至判断出a＞0也比较简单.关键点与难点在于不等式知识在此方法中的运算，并且需要有一定的逻辑推理能力，在压轴题中考查的数学基本能力是学生在平时练习需要归纳总结的.

三、教学反思

上文中对该试题的两问进行了详细的分析，指出了易错点与难点，且对第（2）问进行了多角度的分析.这都是教师在教学、学生在复习中应该高度重视的问题，从而改进教学与学习方法.

1.基本方法的运用要着眼于对此概念的深度理解

在该试题的第（1）问中，学生的易错点与难点：对函数求导之后判断导数的符号.导函数f′（x）=2ae2x+（a-2）ex-1，直接令f′（x）=2ae2x+（a-2）ex-1＞0（＜0），求x的取值范围，一般学生都会手足无措，这一道题基本上也无望得分.这种问题的出现从表现上看是学生的计算能力弱，其实不然，关键还在于学生对二次函数与指数函数概念的理解.基础稍好的学生能够将f′（x）=2ae2x+（a-2）ex-1看作关于ex的二次函数，接下来令导数为0，利用求根方程，讨论a的符号，判断单调性，这是一种基础可行的方法，但是过于复杂，计算过程容易出错.若能观察出导函数可用因式分解的方法转化为f′（x）=（2ex+1）（aex-1），这一问就能大获圆满.这种将复杂因式进行分解的能力在很多高考试题中都考查过，因式分解简单来说就是将一个多项式化为几个最简整式的乘积的形式，学生在初中就学过这样的方法，然而在高中这种方法还是不会用，这就说明基本概念渗透不深刻.

试题第（2）问的思路一考查的是数形结合的方法，只要能根据第（1）问画出函数简图，第（2）问基本上也能解决.学生出错点在于对函数零点存在的必要条件不清楚，在人教版选修1-1中就出现过这样的类似问题.在掌握数形结合的方法下，深度挖掘函数零点存在的条件，这也是一个重要的数学概念.

试题第（2）问的思路2分析中的角度1需要学生掌握的是方程的根与函数零点的关系.函数有两个零点即方程有两个根.利用方程根的定义，设x1，x2为方程的根，不必将x1，x2具体求出（求不出来）.利用恒等式f（x）=0，将a分离出来，接下来讨论与y=a的交点个数.这样的解题思路也是水到渠成的，不需要过多的技巧性，仅需要学生理解方程的根与函数的零点这两个基本概念，分离参数法是学生在众多练习中已经熟练掌握的方法，然而方法的运用总要建立在一定的概念理解之上，才能更好的解题.

2.练习的选择要具有针对性，体现各知识的交互融合

在（1）、（2）两问的分析中，明显感觉到这一试题考查的知识点很多，如函数单调性、函数零点，二次函数等.高中数学知识多，要在一张试卷中涵盖几乎所有知识，试题中必将出现知识的交互融合.没有对高考真题的针对性练习，很难对众多知识融合的试题做出快速简洁的解答，如判断导函数f′（x）=2ae2x+（a-2）ex-1的符号，学生难以动手处理.若是在平时有类似的练习，头脑中的潜在意识就会促使其用因式分解的方法处理.在历年高考题中，经常会碰到函数与导数、函数与不等式、数列与不等式等知识的整合，这都需要学生在平时练习中总结归纳.

3.数学思想方法要渗透在教学中

通过对此试题的研究我们发现，思想方法的考查在高考数学中至关重要，这一试题就考查了分类讨论、数形结合、化归与转化、函数与方程、分离参数法、放缩法等基本思想方法.对思想方法的考查，就是考查学生的数学能力.掌握理解思想方法与否将在考试中区分学生的数学能力.历年的高考数学压轴题都会考查到数形结合的思想，如2016年全国Ⅰ卷理科第21题：已知函数f（x）=（x-2）ex+a（x-1）2有两个零点.（1）求a的取值范围；（2）设x1，x2是函数的两个零点，证明x1+x2＜2.［2］这道试题就考查了数形结合、分离参数、函数与方程等思想方法.又如2016年江苏高考数学第19题：已知f（x）=ax+bx（a，b＞0，a≠1，b≠1）.（2）若0＜a＜1，b＞1，函数g（x）=f（x）-2有且只有一个零点，求ab的值.［3］这道试题考查了数形结合、函数与方程、放缩法等思想方法.文2和文3都对高考试题进行了详细的分析.

四、结束语

本文以2017年高考数学全国Ⅰ卷理科卷的压轴题为研究对象，对高考试题进行了详细的分析，并从多角度给出了解题思路与过程.从反思中得到启示：要深度挖掘教材上的基本概念的含义；要有针对性地练习；在练习中要渗透思想方法的教学.教师在教学中也要引导学生对一个问题进行多角度剖析并对碰到的问题总结归纳，从而培养学生的自主学习能力与反思能力.

1.盛朝阳.2016年高考数学四川卷文科压轴题的研究与反思［J］.中学数学教学参考（下），2017（3）.

2.徐章韬.MKT：化无形思想为有形技巧——基于对一道“函数零点”高考试题的分析［J］.教育研究与评论·中学教育数学，2016（8）.

3.徐坚.转换观点，化繁为简［J］.数学通讯，2016（11，12上）.F