“一元一次不等式（第1课时）”教学设计及立意阐释

☉江苏江阴市青阳第二中学 翟亚雄

☉江苏江阴市青阳第二中学 姚 强

近期，笔者有幸在一次“区域教研”活动中执教“一元一次不等式（第1课时）”（人教版七年级下册第九章第2节），受到参会领导和听课老师的一致好评.下面简单呈现其关键环节（形成概念和探究解法）的教学设计，并对其教学立意进行简单阐释，不当之处，敬请指正.

一、教学设计

1.形成概念.

（1）观察下列一元一次方程，回忆一元一次方程的定义：

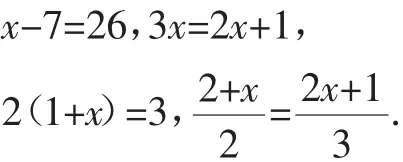
师生行为：教师引导，学生回答.

设计意图：根据维果斯基的“最近发展区”理论，从学生熟悉的一元一次方程入手，意在调动学生学习的积极性和主动性，为本节课的后续学习打下坚实的基础.

（2）类比一元一次方程的定义，给下列不等式下一个定义：

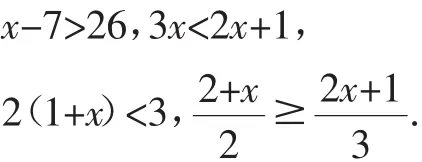
师生行为：学生自主探究，教师在先前形成的“一元一次方程”的定义中将需要修改的部分用红色粉笔改动.

设计意图：在类比过程中发现一元一次不等式与一元一次方程在结构上的相同点和不同点，同时引导学生快速将本节课所学习的新知纳入原有的知识体系中.

练习1：下列不等式哪些是一元一次不等式？为什么？

练习2：若不等式x|a|+3＞2是一元一次不等式，则a=_______.

变式：若不等式（a-1）x|a|+3＞2是一元一次不等式，则a=_______.

师生行为：学生口答，教师追问“为什么”.

设计意图：通过练习1加深学生对一元一次不等式概念的认识，通过练习2及变式加深学生对定义中对未知数的次数和个数的要求的理解.

2.探究解法.

（1）当x满足什么条件时，2+x等于2x-1？

师生行为：教师引导学生列出式子，然后请两位学生板演，其他学生在练习本上完成.教师巡视，巡视过程中督促学生严格按照解一元一次方程的规范步骤书写.

设计意图：同定义的学习一样，仍然从解一元一次方程入手，引导学生回顾解一元一次方程的基本步骤：去分母、去括号、移项、合并同类项、系数化为1.

变式1：将（1）中的“等于”改为“大于”.

变式2：将（2）中的“等于”改为“不小于”.

师生行为：教师引导学生得到式子，然后请一位学生起来回答，在先前形成的解一元一次方程的步骤中用红色粉笔直接修改，并及时追问“为什么”，即可以直接修改的依据.（注意：师生共同完成变式1，学生独立完成变式2）最后教师追问：还可以给出哪些变式？

设计意图：通过变式1和变式2实现由一元一次方程向一元一次不等式的过渡，主要还是为了学生能够在类比中探究一元一次不等式的解法.

变式3：以第（2）题为例.

①前者与后者的和大于1.

②前者与1的差小于后者.

③还有呢？

师生行为：教师首先给出两个例子，引导学生得到式子，然后让学生自主编题，最后请一位学生板演第②题，同时让学生反思此题容易出错的地方：漏乘.

设计意图：通过变式3引入一类在解一元一次不等式中容易出错的题目，即含有常数项的一元一次不等式，在解这类不等式的过程中应该注意“不要漏乘”.

（3）根据下表，找出解一元一次方程和解一元一次不等式的异同点.

要求：以小组为单位，自行讨论3分钟.

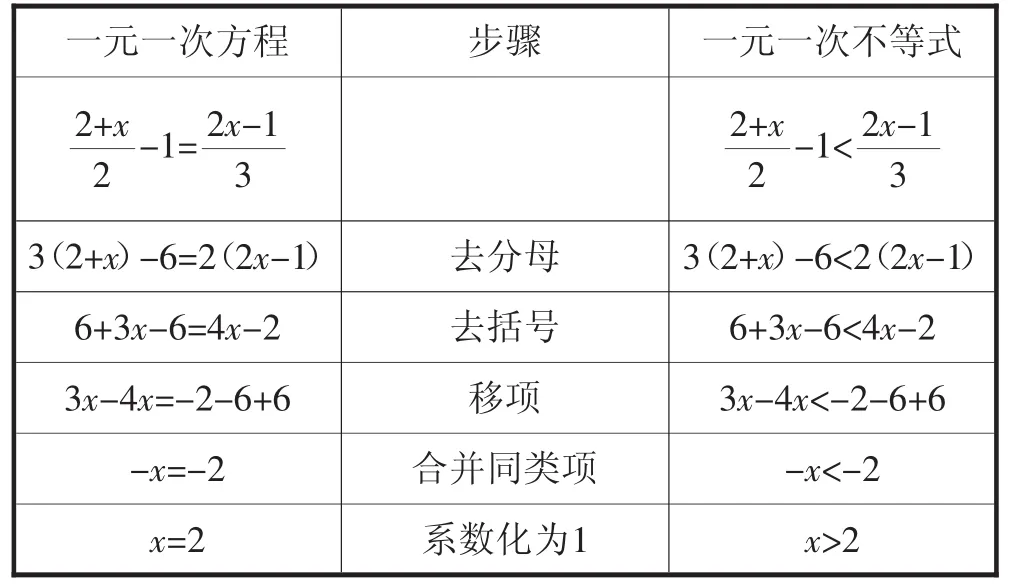
师生行为：教师充分放手，让学生在自主探究、小组合作中给出问题的答案，教师适时引导即可.

最后引导学生归纳得到：解一元一次不等式与解一元一次方程的步骤相似：解一元一次方程，要根据等式的性质，将方程逐步转化为x=a的形式；而解一元一次不等式，则要根据不等式的性质，将不等式逐步转化为x＜a或x＞a的形式.

设计意图：进一步引导学生在类比中归纳一元一次方程和一元一次不等式的相同点和不同点，加深学生对本节课所学内容的认识.

二、教学立意

1.渗透类比，类比有据.

日本数学教育家米山国藏曾经在其论著中指出：“学生在学校所学的数学知识，在进入社会后，几乎没有什么机会应用，因而这种作为知识的数学，通常在出校门后，不到一两年就忘掉了.然而不管他们从事什么职业，那种铭刻于头脑中的数学精神、数学的思维方法、研究方法、推理方法和着眼点等，都随时发生作用，使他们受用终身.”上述论断中提到的“数学精神、数学的思维方法、研究方法、推理方法和着眼点等”正是“数学思想”的体现.此外，《义务教育数学课程标准（2011年版）》也在原来“双基”（基础知识和基本技能）的基础上提出“四基”（基础知识、基本技能、基本思想和基本活动经验），可以看出“数学思想”已经引起相关专家和学者的重视，然而在实际教学中由于受到“应试教育”的影响，真正去落实还有一定的距离，这就需要一线教师在教学中足够重视.

本课例在设计过程中充分注意到了这一点，从定义到解法都在引导学生和前面学习的一元一次方程进行类比，使学生可以比较快速接受新知.此外，更重要的一点（也是非常容易忽略的一点）是在类比过程中应该引导学生明确类比的依据，不但要“知其然”，还要“知其所以然”，教学过程中教师一步步的追问和最后的表格将解一元一次不等式每一步的依据内化于学生的心中，外化于学生的实际行动（从学生的板演可以看出）.

2.突出变式，变式有法.

当学生毕业走出校门以后，数学学科留给学生的印象不应该是一道又一道做不完的题，一张又一张做不完的试卷.然而，数学学科的学习必须辅以一定数量的题目，在一定数量题目的基础上实现质变，那么，怎样才能够使“一定数量”的题目降至最少，切实减轻学生的学业负担，从而使学生喜欢数学、爱上数学呢？

笔者认为，在课堂教学中开展“变式教学”便是一种不错的尝试，通过“变式”可以加深学生对所学内容的理解（练习2及变式），通过“变式”可以沟通不同题目之间的联系（变式1和变式2），同时通过“变式”还可以实现“题目数量的增加”，从而加深学生对相关题目本质的理解，在此基础上真正实现“题目数量的减少”（变式3，特别是③），达到举一反三、触类旁通的教学效果.

三、写在最后

关于本节课的教学，在活动结束后的评课环节，也提出了不少商榷意见，比如，有老师指出：上述设计中忽略了教材中对“移项”的解读，教材中拿出专门的段落对“移项”这一步骤进行了说明，进而指出解一元一次不等式与解一元一次方程有着类似的步骤，这一点在教学中应该引起足够重视，而不仅仅是通过“类比”的方式，简单“滑过”.

对课堂教学的追求是永无止境的，教学也是一门艺术，作为一线教师，应该在教学中对自己不断提出更高的要求，进而走向自身专业成长的快车道.

1.何君青.“链条式”课堂教学的实践与思考——以“有理数的乘法与除法（1）”为例［J］.中学数学（下），2017（10）.

2.沈良琴.对“学材再建构”的尝试与感悟——以“多项式升（降）幂排列”习题课为例［J］.中学数学（下），2017（9）.

3.陈莉.如山水画缓缓展开：习题课的一种教学追求——以全等三角形的证明习题课为例［J］.中学数学（下），2017（9）.

4.李梦娜，万荣庆.重组教学内容结构 渗透三层符号意识——“字母表示数”教学设计与分析［J］.中学数学教学参考（中），2017（10）.