一种LLC谐振变换器的磁集成结构设计方法

熊日辉，姜利亭

(1.中国计量大学 信息工程学院，浙江 杭州310018；(2.杭州寇古科技有限公司，浙江 杭州 311100)

随着直流电源不断向低耗的性能趋势发展，传统硬开关PWM工作模式的充电电源已经不能满足人们追求低损耗、低电磁干扰、高效的性能需求.LLC谐振变换器运用软开关技术，可以提高整个充电电路的转化效率[1-3].虽然LLC谐振变换电路的优点是效率高，实现了初级开关管的零电压开关(ZVS)和次级整流管的零电流开关(ZCS)功能[4].但是其缺点也是显而易见：电路中的磁性元件集成度不高，谐振电路中需要独立变压器和独立电感两个元器件，而且这两个元器件由于体积比较大，以致增大了电源电路的体积，提高了电路设计的成本.为了进一步减少磁性元件的体积和数量，降低LLC谐振电路的设计成本，提高充电电源的市场竞争力，本文提出一种LLC谐振变换器的磁集成拓扑结构的优化设计方法，采用基波分析法和Mathcad软件仿真.仿真实验结果表明，采用磁集成技术对谐振电路效率的提高有一定的可行性和有效性，从而进一步减少了谐振电路的体积和降低了成本.

1 LLC半桥谐振变换器拓扑结构

LLC半桥谐振电路由于结构简单，开关损耗小等优点而被运用到比较多的场合.图1所示的是LLC谐振变换器的等效模型.该拓扑结构主要包括初级2个功率开关管S1、S2；谐振电容Cr、谐振电感Ls、励磁电感Lm；次级整流二极管D3和D4以及输出滤波电容Cf组成.谐振电感是一个独立的变压器磁件，励磁电感是另外一个主电路变压器中的原边电感.这两个变压器占据了电源电路中的大部分位置，增大了体积，而且两个靠近的变压器散发出很大的热量，不利于散热.为了解决上述问题，本文提出了一种LLC谐振变换器的磁集成拓扑结构的优化设计方法.

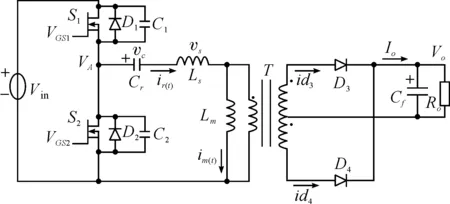
图1 LLC半桥谐振电路拓扑结构Figure 1 LLC half-bridge resonant topology structure

2 磁集成结构设计

对于两个独立的磁性元件集成，要求集成的磁芯具有至少两个以上独立磁支路.而LLC谐振电路中恰好有两个独立的磁性元件：即串联谐振电感和带气隙的变压器.因此，LLC谐振变换器中的激磁电感和变压器之间的集成，可以用绕制一个带气隙的变压器来实现.LLC谐振变换器的磁性元件集成方法主要有两种：第一，利用变压器本身的漏感代替串联谐振电感；第二，通过在变压器磁芯的磁柱上绕制出一个独立的绕组来构造谐振电感.前者由于变压器的漏感本身存在，合理利用漏感代替串联谐振电感是资源再利用的过程；后者增加了独立绕组的成本，而且这增加的绕组在变压器工作时会消耗额外的无用功率，以致降低了电源工作效率.所以本文采用的是前面一种方法，即利用变压器本身的漏感作为串联谐振电感.

2.1 半桥谐振变压器模型

图2是半桥LLC谐振变换器两绕组变压器等效前变压器模型，Vin是两个功率开关管S1和S2的漏源极之间的电压，对应于图1中的VA.Ls1是谐振电感，对应于图1中的Ls.Lm1是激磁电感，对应于图1中的Lm.

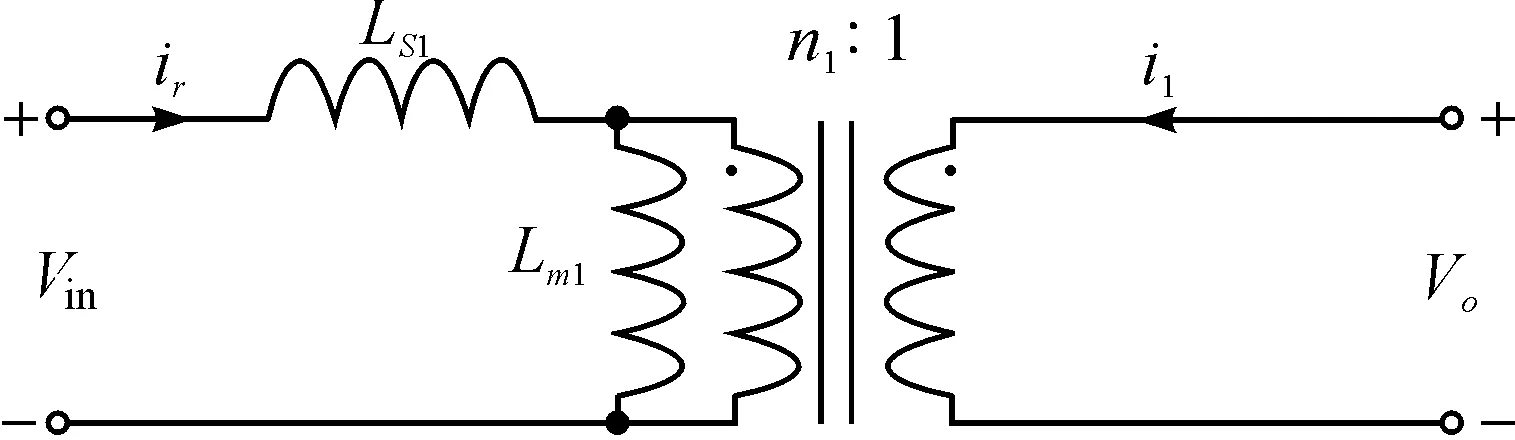
图2 LLC半桥谐振变换器等效前变压器模型Figure 2 Equivalent model of LLC half-bridge resonance converter transformer

2.2 磁集成变压器等效模型

为了对磁集成变压器进行设计，同时利用漏感来构造谐振电感，需要通过等效电路使其达到与原边不存在谐振电感时一样的效果.所以设想将图3中的独立谐振电感和激磁电感集成在一起，通过一定的绕制方式耦合到同一个变压器中，这样可以同时减小磁性元件数目和体积,降低电路功率损耗.

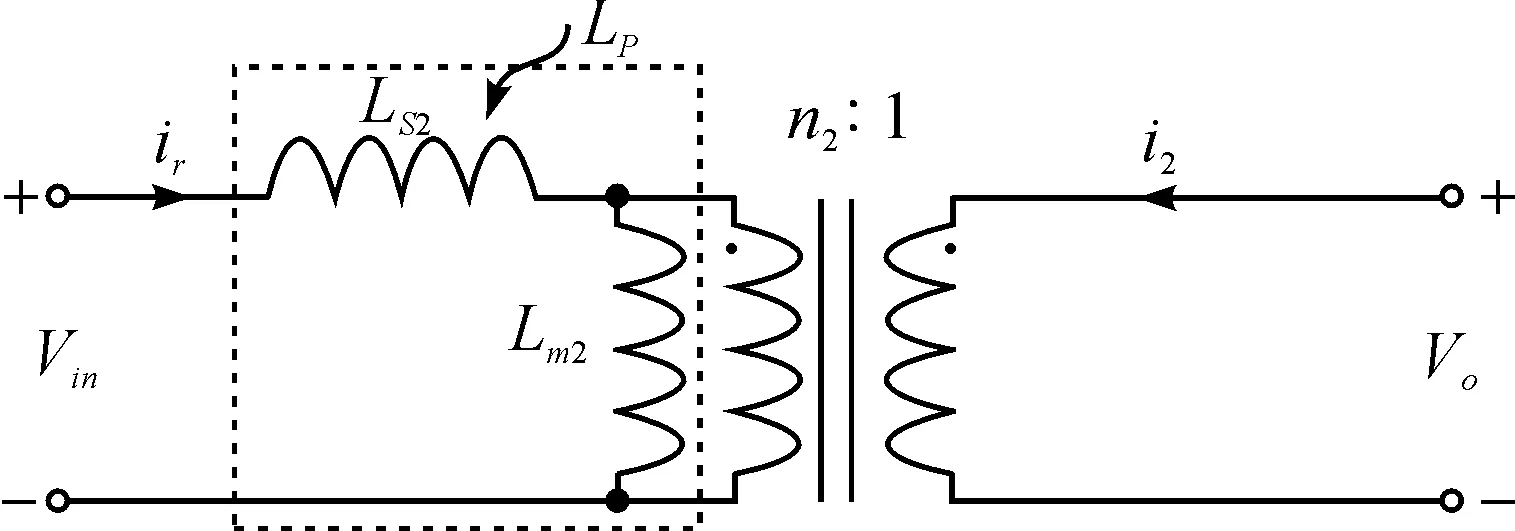
图3 LLC半桥谐振变换器等效后变压器模型Figure 3 LLC half-bridge resonance converter after the equivalent model of the transformer

图4所示的是将独立谐振电感和激磁电感通过带气隙的变压器耦合集成的变压器等效模型.耦合后的激磁电感为Lp.

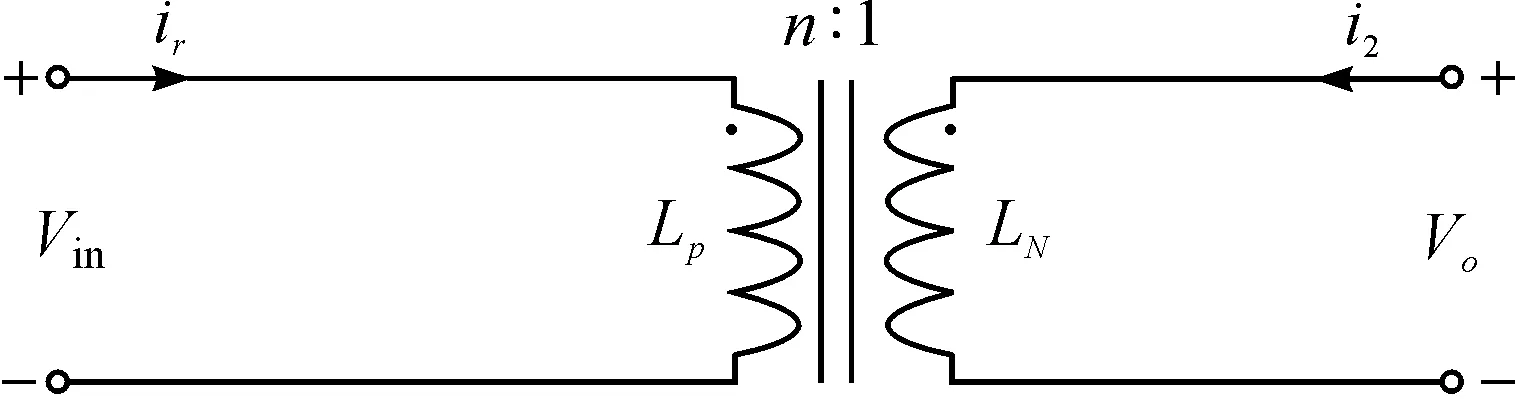
图4 磁集成LLC半桥谐振变压器等效模型Figure 4 Magnetic integrated LLC half-bridge resonance transformer equivalent model

3 磁集成LLC谐振电路设计

3.1 磁集成LLC半桥谐振变换器拓扑结构

按照本文第2小节内容的设计思想和方法，将磁集成变压器等效模型运用到磁集成谐振电路中如图5所示.磁集成拓扑结构主要包括初级2个功率开关管S1、S2；谐振电容Cr、激磁电感Lp.次级整流二极管D3和D4，输出滤波电容Cf组成.由于利用漏感代替谐振电感，而实际变压器T中的漏感是指Lp线圈所产生的磁力线不能全通过次级线圈而产生的漏磁电感，无法在实际电路图中画出，所以将实际变压器中的漏感定义为Ls.

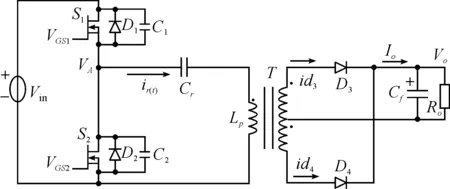
图5 磁集成LLC半桥谐振电路等效模型Figure 5 Magnetic integrated LLC half-bridge resonance circuit equivalent model

3.2 磁集成LLC半桥谐振电路工作原理

在电源电路高频应用场合下，变压器的寄生参数如漏感会引起变压器工作噪声的变化，增大电压尖峰，引起功率开关管的驱动波形占空比会失真.所以如何利用变压器的漏感，特别是对于本文设计的LLC谐振变换器如何利用变压器漏感代替谐振电感，实现磁性元件集成技术，显得非常重要.而常规工程中设计的LLC变换器中的谐振电感和变压器激磁电感数值是比较接近的，所以其漏感比较小.而在磁集成谐振电路中，其漏感会比之前变大.若漏感量太大，变压器将原边的能量传递给副边的能量过程中则会损失一部分在漏感上，谐振电路的输入电压与输出电压增益关系就不能达到预期的要求[5-6].而激磁电感的感量值相对要求会较小，要减小激磁电感的感量值，最简单有效的方法就是增大气隙.因此本文研究磁集成的设计，从电压增益关系上作深入分析，采用基波分析法来实现，并用Mathcad软件仿真，进行磁集成谐振电路参数设计和优化.

由于本文研究的是利用变压器漏感作为谐振电感，在高频应用场合下，除了变压器的寄生参数会影响到谐振工作状态外，还有一个重要的参数就是功率开关管的寄生电容.如何充分利用好这两个元件的寄生参数，对磁集成谐振电路的研究具有重要的意义.下面就围绕这两个参数进行磁集成谐振电路设计和优化.

图6和图7所示的是两个功率开关管S1和S2交替导通和关断的电路等效模型图.当S1开通时，S2关断；当S1关断时，S1开通.图中电流Ir是谐振电流ir(t)的最大值，在两开关管交替开通和关断瞬间时谐振电路可以等效成是一个恒流源(电流大小为Ir)，分别对两个功率开关管内的寄生电容C1和C2进行放电，寄生电容C1=C2=Coss.二极管D1和D2分别是两个功率开关管的体二极管.图6中，当开关管S1开通、S2关断时，开关管S1的寄生电容C1上的电压开始放电，为了实现开关管ZVS，使S1开关管上的电压VGS1放电到零时才对S2开关管的极间电容充电，直到S1漏源极间电压为零，此时S1体二极管D1开始导通.图7中，当开关管S1关断、S2开通时，开关管S2极间电容C2上的电压开始放电，同样为了实现开关管ZVS，使S2开关管上的电压VGS2放电到零时才对S1开关管的极间电容充电，直到S2漏源极间电压为零，此时S2体二极管D2开始导通.

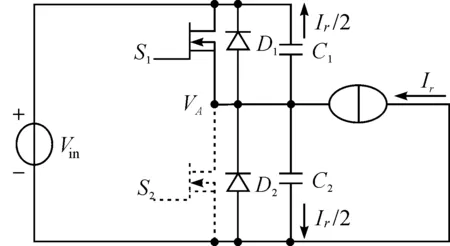
图6 开关管S1开通&S2关断Figure 6 Switch tube S1 open and S2 shut off

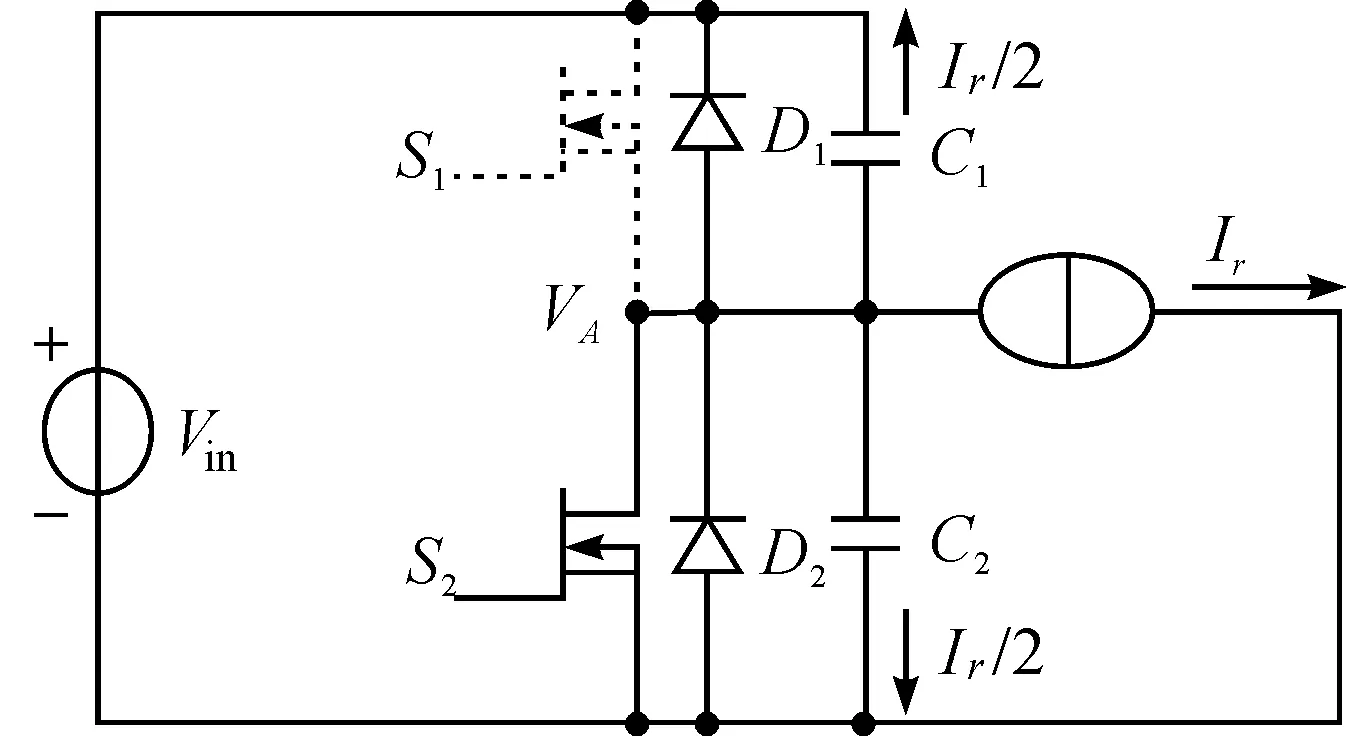
图7 开关管S1关断&S2开通Figure 7 Switch tube S1 shut off and S2 open

3.3 磁集成LLC半桥谐振电路谐振元件参数设计方法

由图8中可以看出，在(0～t0)时间段内，谐振电感和谐振电容发生谐振，电流im线性增加.为了实现开关管ZVS，使S1开关管上的电压VGS1放电到零时才对S2开关管的极间电容充电.

(1)

ir(t)=Irsin(wst-φ).

(2)

式(1)中：Im是最大励磁电流，n是变压器T匝数比，Vo是输出电压.ws,φ分别是电流ir的角频率和初相角，Ir是电流ir的最大值.

在(to～t1)之间必须插入一个死区时间，此时电流id3和id4刚好降为零，励磁电感电流达到最大值Im，实现次级整流二极管的ZCS[7-8].因为死区时间很短，为了简化公式计算，我们在公式运算中忽略了死区时间.我们定义to=t1/2，t1=T/2；在另外一个对称的半周期内，我们也可以定义t2=T1，t3=T.

(3)

式(3)中Im是最大励磁电流，T1为功率开关管开关周期，Vo是输出电压，n是变压器T匝数比.

在时间段(0～t1)内,当负载电流为Io时，谐振电容Cr被线性充电.充电电流为变压器原边电流传递到副边电流的平均值Io/n，Cr两端电压Vc对称的从最小电压Vcmin到Vcmax，所以

(4)

式(4)中Io是输出电流，Ir是谐振电流ir(t)的最大值.

因为Cr在电路发生谐振时会储存一定量的电能，传递到输出端的功率随着Cr变小而变大，Vc就会变高.所以接下来要对Cr电容的峰值电压Vcmax做近似的分析.在(0～t1)时间内，储存在Cr两端电压是在t1时间点达到最大电压的Vcmax变化量：

(5)

(6)

根据公式(5)和(6)可以得出

(7)

(8)

(9)

式中fs=1/T1为开关管的开关频率，所以选择最小励磁电流Immin，将我们关注的漏感参数和寄生电容参数整合到电压传输增益公式中,所以可以得到最小Immin公式为

根据公式(3)、(6)、(7)可得出

(10)

式中nselect实际变压器选择的匝数比，Vomax为最大输出电压.

设计谐振网络参数重点在于根据ZVS和ZCS条件[9-11]，调节Lm，Cr，Ls的参数值，获得输入电压关于归一化频率fn=fs/fr1(开关频率与第一谐振频率之比)，品质因素Q，和h(Ls/Lm)的输出电压传递函数m(fn,h,Q)关系.而运用Mathcad软件可以对上面公式进行参数优化选择，了解谐振电路电压增益传输的幅频特性.

式中Ls为变压器漏感，Q为品质因数，Romax为最大输出电阻，Romin为最小输出电阻.

Vout(Vin,h,α)=

(11)

Voutl(Vin,h,α)=

(12)

式(11)中Vout(Vin,h,α)是输出最大电压增益函数.

式(12)中Voutl(Vin,h,α)是输出最低电压增益函数.

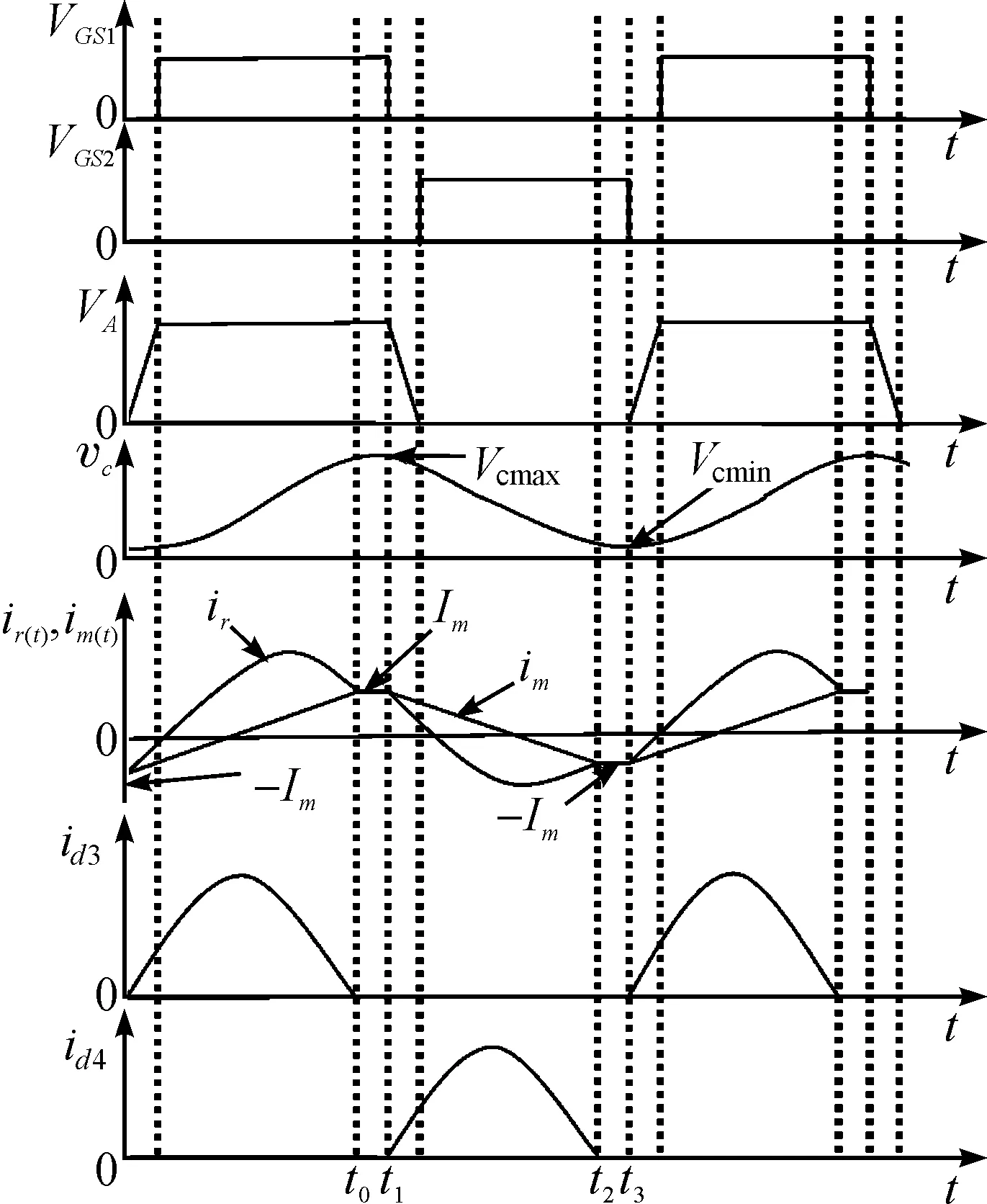
图8 LLC磁集成谐振电路理想工作波形图Figure 8 Magnetic resonance circuit integration ideal work waveform

3.4 磁集成LLC半桥谐振电路谐振元件参数设定

本文根据上述磁集成LLC半桥谐振电路设计原理和方法，组装了一台输出功率Po=1 045 W，输出电流Io=14.5 A，输出电压Vo=52～72 V的样机.在实际工程设计中电源负载调整率一般在60%～100%之间，所以设置最低输出电压Vomin=114.943 V.具体参数设定根据实际应用设定如下表：

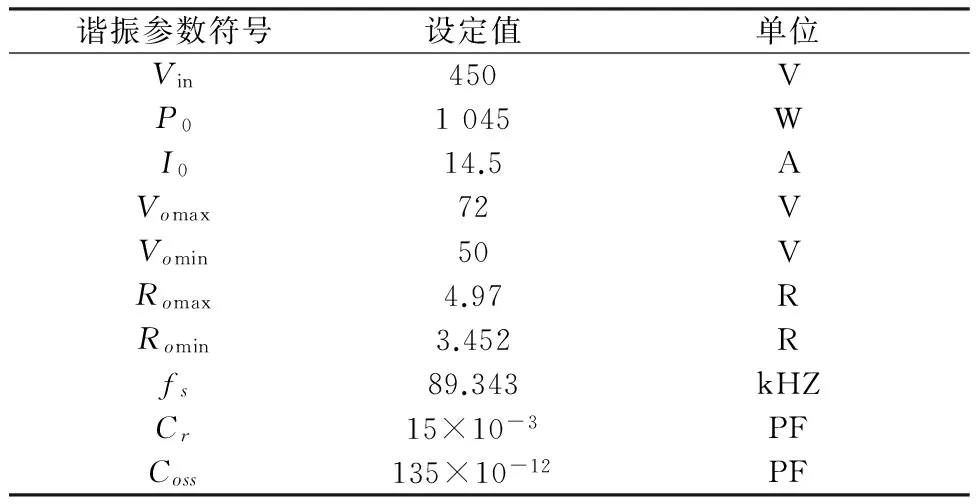
表1 磁集成谐振元件参数表

4 Mathcad电压增益仿真波形与测试波形分析

4.1 Mathcad电压增益仿真波形分析

设计谐振网络参数重点在于根据ZVS和ZCS条件，调节激磁电感，谐振电容，谐振电感的参数值.本章节将两个容易被忽视的参数(变压器漏感和功率开关管寄生电容)考虑到半桥LLC谐振电路工作中，以获得理想输入电压关于归一化频率α，Vin和h的输出电压传递函数Vout(Vin,h,α)关系.并用Mathcad软件仿真，进行磁集成谐振电路参数设计和优化，了解电压传输增益的幅频特性.

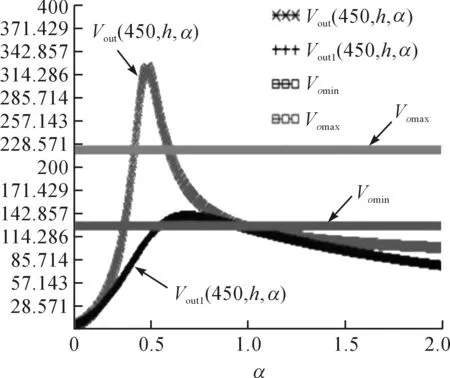
图9 电压增益仿真曲线Figure 9 Voltage gain simulation curve

图9所示的本章节设计研究的磁集成LLC半桥谐振电路的输出电压增益仿真曲线.Vout(450,h,α)是最大电压增益曲线，Vomax是最大输出电压220 V曲线，这两条曲线交于两点(α=0.4和α=0.6).由于α=0.4在曲线α=0.5(电压增益最高点)的左边，频率逐渐增大时，增益曲线会出现拐点，所以在相同的频率范围内，电压变化速度较大.为了防止这样的情况，在实际工程谐振参数的设计中，参考拐点右边的增益曲线.当α=0.6时，开关频率为53.6 kHz，所以在实际电路设计中只要设计谐振电路的最小频率在45 kHZ和50 kHZ就可以.Voutl(450,h,α)代表最小输出电压增益曲线，Vomin是60%载电压114.943 V，当电路输出最小电压时，α=1，开关频率为89.343 kHZ.所以电路在全负载范围内(114.943 V～220 V)调节时，开关频率只变化了2倍频率左右，提高了磁集成电路的效率，效率达到了92.7%，比谐振半桥LLC谐振电路工作效率提高了1.2%.

4.2 LLC半桥谐振电ir(t)测试波形分析

图10为本文设计的样机工作在最大功率时的谐振电流测试波形和谐振功率开关管驱动波形，VGS1是S1开关管驱动测试波形，VGS2是S2开关管驱动测试波形，VGS1驱动波形和VGS2驱动波形交替上升，图中的A点下降沿正好对应图中B点的上升沿，ir(t)是谐振电流测试波形，A点对应谐振电流ir(t)的C点是图8中ir(t)的-Im处；B点对应谐振电流ir(t)的D点是图8中ir(t)的Im处；图8中的VGS1和VGS2的上升沿和下降沿也是对应ir(t)的-Im和Im两处.由图10可知该谐振电流波形形状趋于正弦电流波形，证明本文研究的磁集成结构设计具有可行性和有效性.

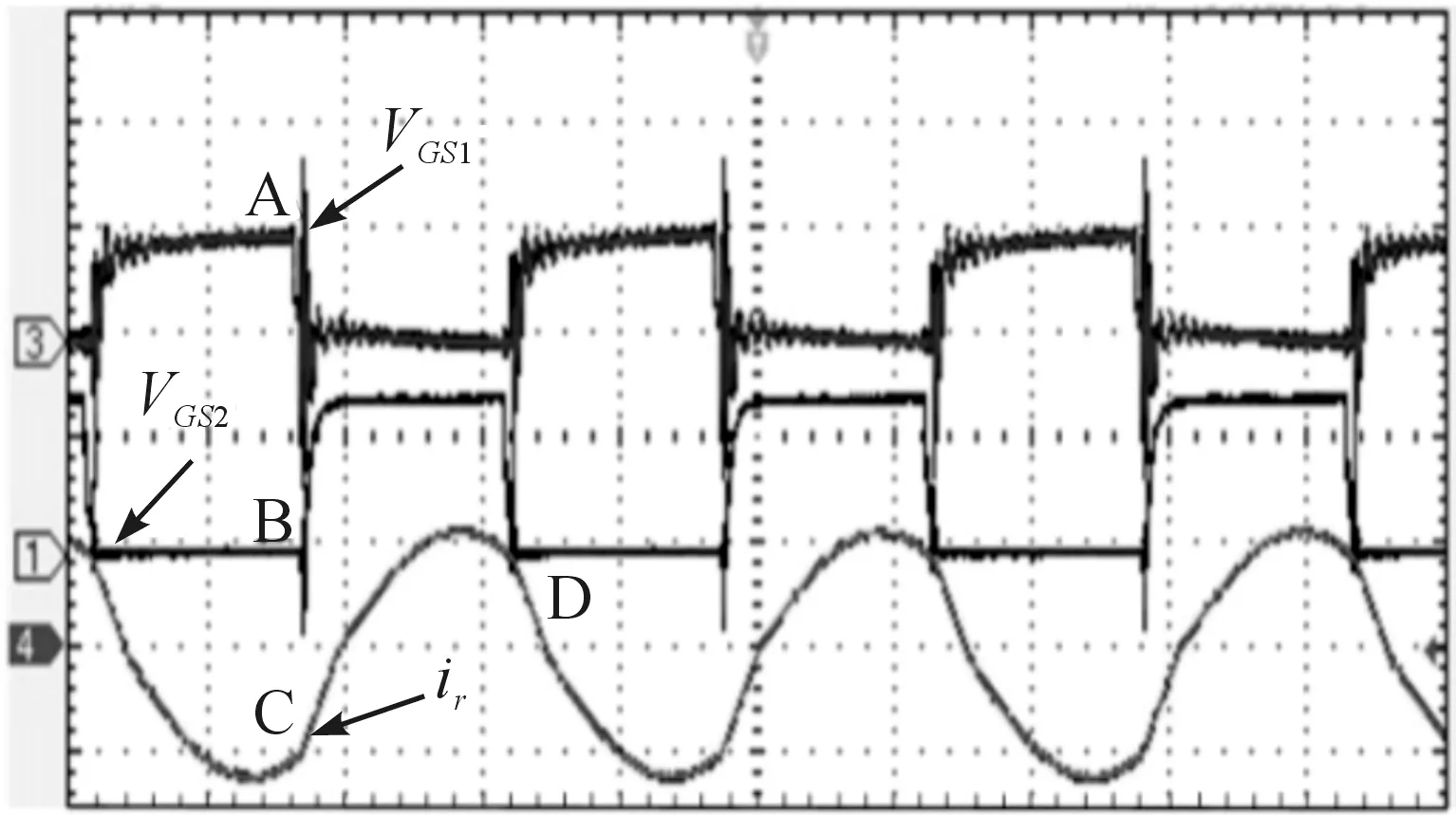
图10 谐振电流波形Figure 10 Resonant current waveform

5 结 语

本文基于在对LLC谐振变换器研究的基础上，介绍了磁集成LLC谐振变换器的主电路结构和设计方法.利用变压器漏感作为谐振电感，将变压器漏感和功率开关管寄生电容考虑到磁集成LLC半桥谐振电路工作中，采用基波分析法分析输入电压与输出电压增益关系，并用Mathcad软件仿真，进行磁集成谐振网络参数设计和优化.并将优化的磁集成技术运用到本文所要设计的样机中，电源电路工作效率达到92.7%.仿真实验测试结果表明，采用磁集成技术对谐振电路效率的提高有一定的可行性和有效性.

[1] BEIRANVAND R, RASHIDIAN B, ZOLGHADRI M R, et al.A design procedure for optimizing the LLC resonant converfer as a wide output range voltage source.[J].IEEETransactionsonPowerElectron, 2012, 27(8): 3749-3763.

[2] MUSAVI F, CRACIUN M, GAUTAM D S, et al. An LLC resonant DC-DC converter for wide output voltage range battery charging applications[J].IEEETransactionsonPowerElectron,2013, 28(12): 5437-5445.

[3] FEI C, FRED C L,QIANG L H. High-efficiency high-power-density LLC converter with an integrated planar matrix transformer for high-output current applications[J].IEEETransactionsonIndustrialElectronics,2017, 64(11):9072-9082.

[4] 吴建明, 汪伟, 蔡慧. LLC谐振变换器模糊自适应控制研究[J].中国计量大学学报,2017,28(2):196-202.

WU J M, WANG W, CAI H. Research on adaptive control of LLC resonant converters[J].JournalofChinaUniversityofMetrology, 2017,28(2):196-202.

[5] 刘和平,陈红岩,苗轶如,等.混合式LLC电路谐振与同步整流数字式控制[J].中国电机工程学报, 2015, 35(9): 2272-2278.

LIU H P, CHEN H Y, MIAO Y R, et al. Hybrid LLC circuit resonant and synchronous rectifier digital control[J].ProceedingsoftheCSEE, 2015, 35(9): 2272-2278.

[6] GAO X, WU H F, XING Y. A multioutput LLC resonant converter with semi-active rectifiers[J].IEEEJournalofEmergingandSelectedTopicsinPowerElectronics, 2017, 5(4): 1819-1827.

[7] QIAN T. An adaptive current injection scheme for resonant capacitor of LLC resonant converters with suppressed frequency variation[J].IEEETransactionsonPowerElectronics, 2016, 31(12): 8074-8080.

[8] MURATA K, KUROKAWA F. An interleaved PFM LLC resonant converter with phase-shift compensation[J].IEEETransactionsonPowerElectronics,2016, 31(3): 2264-2272.

[9] KOJI M, FUJIO K. Performance characteristic of interleaved LLC resonant converter with phase shift modulation[C]// 2015IEEEInternationalTelecommunicationsEnergyConference(INTELEC). Japan: IEEE Xplore, 2015:1-5.

[10] BOSCAINO V, MICELI R, BUCCELLA C, et al. Fuel cell power system with LLC resonant DC/DC converter[C]//2014IEEEInternationalElectricVehicleConference(IEVC).Italy: IEEE Xplore, 2014: 1-6.

[11] CONCETTINA B, CARLO C, HAMED L, et al. Observer-based control of LLC DC/DC resonant converter using extended describing functions[J].IEEETransactionsonPowerElectronics, 2015, 30(10): 5881-5891.