SOT-不可分离Witness的比较

柴晋飞，侯晋川

(太原理工大学 数学学院，太原 030024)

纠缠现象是量子力学区别于经典力学的突出特征之一。在量子信息理论中，纠缠态作为一种物理资源，在量子通讯、秘钥分配、隐形传态等方面都发挥着重要的作用[1]。近年来，纠缠的刻画引起了众多学者的关注[2-12]。

用算子理论语言，一个量子态可以表示为某个可分复Hilbert空间上迹为1的正线性算子，用S(H)表示H上的所有态构成的集合。设ρ是Hilbert空间张量积H=H1⊗H2上的量子态。如果ρ可以表示成

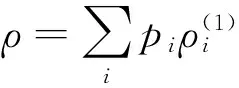
或者形如上述算子的迹范数拓扑极限，则称量子态ρ是可分离的；否则，称ρ是纠缠的。

于是纠缠性的检测问题等价于刻画Hilbert空间张量积H=H1⊗H2上的迹为1的正迹类算子在什么条件下能表示为Hi(i=1,2)上迹为1的正迹类算子的张量积的凸组合或者这种凸组合的极限。

笔者把可分离量子态的概念推广到一般有界线性算子情形，引入SOT-可分离正算子的概念并给出SOT-不可分离性的Witness判据；文献[13]中应用SOT-可分离性的一些性质应用于可分离量子态研究，给出一类新的可分离量子态及其判别方法。

记T(H)为H上迹类算子空间，B(H)为H上所有有界线性算子组成的von Neumann (vN)代数。由于量子态的全体S(H)是T(H)的单位球面中的闭凸子集，而B(H)的单位球面中正算子全体的集合不一定是凸的，所以只能对一般正算子引入可分离性概念。

由SOT-不可分离性的Witness判据，对于任意一个SOT-不可分离正算子，总存在一个SOT-不可分离Witness能检测到它。但是并不存在一个万能的Witness能检测到所有的SOT-不可分离正算子。于是探讨两个不同witness之间的关系是有着基本重要性的问题。本文的目的是探讨无限维张量积空间中不同SOT-不可分离Witness之间的关系，以及最优SOT-不可分离Witness的结构性质。

1 预备知识

记B(H)为H上所有有界线性算子组成的von Neumann(vN)代数。因为B(H)中范数为1的正算子全体的集合不是凸的，所以只能对一般正算子引入可分离性概念。在本文中，令H1，H2是可分的复Hilbert空间，总假设dim(H1⊗H2)=∞.下面，给出本文需要的一些定义和引理。

设A∈B(H1)为有界线性算子，如果〈Ax,x〉≥0对所有的x∈H1都成立，则称A为正算子，记为A≥0.记B+(H1)，B+(H2)，B+(H1⊗H2)分别为H1，H2，H1⊗H2上的正算子全体。

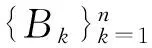
或者A可以写成形如上述算子的强算子拓扑极限，则称A是强算子拓扑可分离的，简称为SOT-可分离的；否则，称A是SOT-不可分离的。记BSOT为H1⊗H2上的SOT-可分离算子全体组成的集合。显然，BSOT是B(H1⊗H2)中的一个SOT-闭的凸锥。下面结果是SOT-不可分离性的witness判据。

引理1A∈B+(H1⊗H2)，则A是SOT-不可分离的当且仅当存在有限秩自伴算子W使得Tr(WA)<0而Tr(WC⊗D)≥0对任意C∈B+(H1)，D∈B+(H2)都成立。

上述引理中的有限秩自伴算子W称为SOT-不可分离witness.显然W不是正的。

设Ω为H1⊗H2上的所有SOT-不可分离Witness构成的的集合，即

Ω={W∶W∈B(H1⊗H2)，W*=W，Tr(WA)≥0，A∈BSOT，W为有限秩且W非正} .

对于W∈Ω，Γ⊂Ω，定义

ΔW={A∶A∈B+(H1⊗H2)，Tr(WA)<0}，ΔΓ=∩W∈ΓΔW.

显然ΔW和ΔΓ都是凸集。

定义2 设W1，W2∈Ω，如果ΔW2⊂ΔW1，则称W1比W2更优，记为

W2W1.

特别地，设W为SOT-不可分离witness，如果不存在比W更优的SOT-不可分离Witness，则称W是最优SOT-不可分离Witness.

对任意W1，W2∈Ω，如果W1W2或W2W1，则称W1和W2是可以比较的；否则，它们是不可比较的。特别地，如果W1W2且W2W1，称W1和W2是等价的。

一般而言，任意两个WitnessW1和W2之间有3种关系：

1)W1W2或W2W1，特别地ΔW2=ΔW1；

2) ΔW1∩ΔW2≠Ø且ΔWi⊄ΔWj，i,j=1,2且i与j相异；

3) ΔW1∩ΔW2=Ø.

下面给出本文用到的其它术语和符号。

1) 设H为可分的复Hilbert空间，H'是H的子空间。如果H'中所有元的线性组合构成的子空间在H中稠密，则称H'张成H.

2) 设A∈B(H1)是有界线性算子，{xi}为H1上的一组标准正交基，AT表示A相对于这组基的转置。

3) 设A∈B(H1⊗H2)是H1⊗H2上的有界线性算子，AT2表示对A按H2取偏转置。

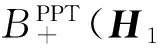
2 可比较的SOT-不可分离Witness

对于任意给定的两个SOT-不可分离WitnessW1和W2，给出它们可比较的充分必要条件。首先给出几个引理。

引理2 如果W∈Ω，则存在一个SOT-可分离正算子A∈BSOT使得Tr(WA)>0.

证明：显然SOT-不可分离Witness是纠缠Witness，故由引理1知，存在一秩投影P∈B+(H1)，Q∈B+(H2)，使得Tr(WP⊗Q)>0，从而本引理得证. 但是文献[14]的证明有误，故此在这里先给出引理1的证明。

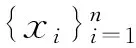
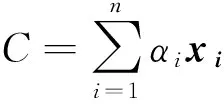
Tr(WC⊗D)=∑i,jαiβj(WPi⊗Qj)=
∑0=0 .

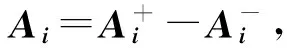
引理3 设W1,W2∈Ω.如果W1W2，则且对任意A∈B+(H1⊗H2)，都有Tr(W2A)≤λTr(W1A).

证明：注意λ≧0.对任意的A∈B+(H1⊗H2)，分下面3种情形来考虑：

1) Tr(W1A)=0.欲证Tr(W2A)≤λTr(W1A)，仅需证明Tr(W2A)≤0.假设Tr(W2A)>0.对于任意A∈ΔW1⊆ΔW2，a>0，令A(a)=A1+aA，则

Tr(W1A(a))=Tr(W1A1)+aTr(W1A)=
Tr(W1A1)<0，

所以A(a)∈ΔW1⊆ΔW2.

2) Tr(W1A)>0.对任意A1∈ΔW1，令A'=[Tr(W1A)A1-Tr(W1A1)A]，则Tr(W1A')=0.由情形一已证的结果可知Tr(W2A')≤0，因此，

Tr(W1A)Tr(W2A1)≤Tr(W1A1)Tr(W2A)，

最后证明λ>0.假设λ=0，则存在一个序列{An}⊂ΔW1使得

(1)

由引理2及前面的证明可知，存在T∈BSOT使得Tr(W1T)>0且Tr(W2T)>0.令

则Tr(W1A'n)=0，故由第一种情形可知，Tr(W2A'n)≤0对任意n都成立。然而，

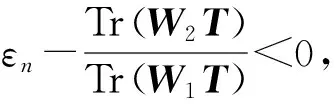
下面是本节主要结果。

定理1 设W1，W2∈Ω，则

1)W1W2当且仅当存在正数a>0和有限秩正算子D≥0使得W1=aW2+D.

2) ΔW1=ΔW2当且仅当存在正数a>0使得W1=aW2.

证明：

1) 假设存在正数a>0和有限秩正算子D使得W1=aW2+D.对任意A∈ΔW1，Tr(W1A)=aTr(W2A)+Tr(DA)<0，所以Tr(W2A)<0，故ΔW1⊂ΔW2.

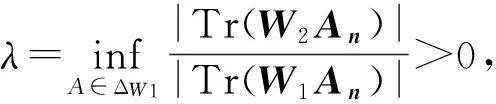
2) 充分性显然，仅证必要性。

设ΔW1=ΔW2.由式(1)可知，存在有限秩正算子Di≥0以及正数ai>0(i=1,2)使得W1=a1W2+D1且W2=a2W1+D2，则W1=a1a2W1+a1D2+D1，因此，

(1-a1a2)W1=a1D2+D1≥0 .

事实上，1-a1a2=0，否则，若1-a1a2>0，则(1-a1a2)W1非正，矛盾；若1-a1a2<0，而(1-a1a2)W1≥0，那么W1≤0.所以对于任意B∈BSOT，Tr(W1B)≤0.因为W1为SOT-不可分离Witness，所以Tr(WB)=0.另一方面，由引理2可知，至少存在一个可分离正算子B使得Tr(W1B)=0，矛盾，故a1a2=1.因此，D1=D2=0，即W1=a1W2.证毕。

3 最优SOT-不可分离Witness

本节给出判断最优SOT-不可分离Witness的条件以及可分解最优SOT-不可分离Witness的结构特征。

定理2 设W∈Ω，则W是最优的当且仅当对任意正数a>0和非零有限秩算子D≥0都有W'=aW-D∉Ω.

证明：假设W不是最优的，则存在与W线性无关的W'∈Ω使得WW'.故存在有限秩算子D≥0和正数a>0使得W=aW'+D，所以W'=a-1W-a-1D.

假设存在非零有限秩算子D≥0和正数a>0使得W'=aW-D∈Ω，则W=a-1W'+a-1D.由定理1，WW'，故W不是最优的。证毕。

利用定理2可以得到判别SOT-不可分离witness为最优的充分条件。令

∏W={x⊗y∈H1⊗H2∶
〈Wx⊗y,x⊗y〉=0} .

(2)

引理4 设W∈Ω，∏W为式(2)中的集合，则对任意满足D∏W≠{0}的有限秩正算子D∈B+(H1⊗H2)及任意正数a>0都有W-aD∉Ω.

证明：设D∈B+(H1⊗H2)为有限秩正算子且D∏W≠{0}，则存在张量积向量x0⊗y0∈∏W使得〈Dx0⊗y0,x0⊗y0〉>0.令A0=(x0⊗x0)⊗(y0⊗y0)，其中，(x0⊗x0)z=〈z,x0〉x0,z∈H1，表示一秩算子。显然，A0是SOT-可分离的，且当a>0时，Tr[(W-aD)A0]=-aTr(DA0)<0，所以W-aD∉Ω.证毕

由定理2及引理4，下面的推论显然成立。

推论1 设W∈Ω.如果∏W张成全空间H1⊗H2，则W是最优的。

下面讨论可分解最优Witness的结构性质。首先回忆一些概念：设A∈B(H1⊗H2)为自伴算子，如果存在正算子P,Q≥0使得A=P+QT2，则称A是可分解的；否则，称A是不可分解的。

定理3 设W∈Ω是可分解SOT-不可分离Witness，则下列等价：

1)W是最优的。

2) 存在有限秩正算子Q使得W=QT2，并且不存在满足R(A)⊆R(Q)的有限秩正算子A使得AT2≥0.

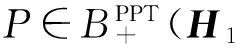
证明：3)⟹1)显然。

1)⟹2)设W可分解的，则存在有限秩正算子P,Q使得W=P+QT2.假设P≠0.因为对任意C∈B+(H1)，D∈B+(H2)，

Tr(QT2C⊗D)=Tr[QT2(C⊗D)]T2=
Tr[(C⊗D)T2(QT2)T2]=
Tr(C⊗DTQ)=Tr(QC⊗DT)≥0 .

所以，QT2∈Ω，故WQT2，与W的最优性矛盾，因此，P=0，W=QT2.

推论2 设W∈Ω为可分解SOT-不可分离Witness.如果W是最优的，则WT2≥0.

4 不可比较的SOT-不可分离Witness

本节讨论不可比较的SOT-不可分离Witness能检测同一个SOT-不可分离正算子的条件。

定理4 设W1,W1∈Ω，则ΔW1∩ΔW2当且仅当存在实数0<λ<1使得W=λW1+(1-λ)W2≥0.

证明：充分性显然，仅证必要性。

记W(a,b)=aW1+bW2，其中，a,b>0.显然，

1) 如果W1W2，W1W(a,b)W2.特别地，它们的凸组合也是Witness.

2) 如果W=aW1+bW2≠0，其中a,b≥0，则

ΔW1∩ΔW2⊂ΔW且ΔW⊂ΔW1∪ΔW2.

3) 设W,W1,W2∈Ω，如果ΔW1∩ΔW2=Ø且ΔW⊂ΔW1∪ΔW2，则ΔW⊂ΔW1或ΔW⊂ΔW2.

设ΔW1∩ΔW2=Ø.令W(λ)=λW1+(1-λ)W2，0≤λ≤1.由2)和3)知，ΔW(λ)⊂ΔW1或ΔW(λ)⊂ΔW2.注意到，当λ从0到1连续变化时，ΔW(λ)从ΔW2连续变化到ΔW1.记λ0=sup{λ∶ΔW(λ)⊂ΔW2}.可以断言，如果ΔW(λ0)⊂ΔW2，则存在0<ε<1-λ0使得W(λ0+ε)≥0.否则，对任意的0<ε<1-λ0，ΔW(λ0+ε)≠Ø，且ΔW(λ0+ε)⊂ΔW1.所以对任意A∈ΔW(λ0)，Tr[W(λ0)A]<0，Tr[W(λ0+ε)A]≥0；另一方面，因为Tr(W1A)≥0，Tr(W2A)<0，故当ε充分小时，

Tr[W(λ0+ε)A]=Tr[W(λ0)A]+
ε[Tr(W1A)-Tr(W2A)]<0 .

矛盾。类似可证，如果ΔW(λ0)⊂ΔW1，则存在0<ε<λ0使得W(λ0-ε)是一个正算子。证毕。

由定理4及证明可直接得到下面的结论：

定理5 设W1,W2∈Ω，则ΔW1∩ΔW2≠Ø当且仅当对任意的0≤λ≤1都有W=λW1+(1-λ)W2∈Ω.

定理4和定理5可以被推广到有限多个Witness的情形。

记cov(Γ)为Γ的凸包，即

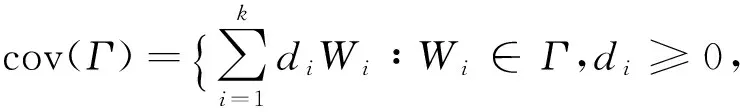
定理6 设Γ={Wi∶1≤i≤n}⊆Ω是由SOT-不可分离Witness构成的有限子集。则：

1) ΔΓ=Ø当且仅当cov(Γ)中包含正算子。

2) ΔΓ≠Ø当且仅当cov(Γ)⊂Ω.

[1] NIELSEN M A,CHUANG I L.Quantum computatation and quantum information[M].Cambridge:Cambridge University Press，2000.

[2] CLARISSE L,WOCJAN P.On independent permutation separability criteria[J].Quantum Inf Comput,2006,6(3):277-278.

[3] GÜHNE O.Characterizing entanglement via uncertainty relations[J].Phys Rev Lett,2004,92(11):117903.

[4] HORODECKI M，HORODECKI P,HORODECKI R.Separability of mixed states: necessary and sufficient conditions[J].Phys Rev A,1996,223(1):1-8.

[5] HORODECKI M，HORODECKI P，HORODECKI R.Inseparable two spin- density matrices can be distilled to a singlet form[J] Phys Lett A,1997,78(4):574-577.

[6] HORODECKI M，HORODECKI P.Reduction criterion of separability and limits for a class of distillation protocols[J].Phys Rev Lett,1999,59(6):4206-4216.

[7] PERES A.Separability criterion for density matrices[J].Phys Rev Lett,1996,77(8):1413-1415.

[8] WERNER R F.Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model[J].Phys Rev A,1989,40(8):4277-4281.

[9] HOU J C，QI X F.Constructing entanglement witnesses for infinite-dimensional systems[J].Phys Rev A,2010,81(6):062351.

[10] STØRMER E.Separable states and positive maps[J].Journal of Functional Analysis,2008,254(8):2303-2312.

[11] QI X F，HOU J C.Positive finite rank elementary operators and characterizing entanglement of states[J].Journal of Phys A:Math Theor,2011,44(21):215305.

[12] HOU J C.A characterization of positive linear maps and criteria of entanglement for quantum states[J].Journal Phys A:Math Theor,2010,43:385201.

[13] HOU J C,CHAI J F.Constructing separable states in infinite-dimensional systems by operator matrices[J].International Journal of Theoretical Physics,2016,56(1):1-10.

[14] HOU J C，GUO Y.When different entanglement witnesses detect the same entangled states[J].Physical Review,2010,82(5):052301.

[15] 侯晋川，崔建莲.算子代数上的线性映射引论[M].北京：科学出版社，2002.

[16] DOUGLAS R G.On majorization and range inclusion of operators in Hilbert space[J].Proc Amer Math Soc,1966,17(2):413-415.