普通轨与槽型轨对现代有轨电车小半径曲线通过能力的影响*

汪振国 雷晓燕 罗 锟

（华东交通大学铁路环境振动与噪声教育部工程研究中心，330013，南昌∥第一作者，硕士研究生）

目前，在国内外现代有轨电车轨道中，普通钢轨与槽型轨均有使用［1-2］。普通钢轨是我国铁路中常用的钢轨类型，技术成熟，与我国车辆车轮踏面匹配度好，在我国现代有轨电车轨道系统中主要采用CHN50与CHN60轨。当轨行区需要绿化或铺面时，槽型轨优势明显，故在开放式或半封闭式的轻轨系统，且以地面敷设方式为主的轨道中，一般推荐采用槽型轨。欧洲现代有轨电车轨道系统中主要采用59R2与60R2槽型轨。车辆方面，现代有轨电车普遍以100%低地板有轨电车为主，其有3种结构形式：单车型、浮车型和铰接型［3］。单车型有轨电车较之其他车型，具有车体受力均匀、编组灵活、车轮磨耗少等优点，在国内外应用较为广泛。

专家学者对有轨电车的研究大多集中在轮轨和车辆的动力学性能方面。文献［4-6］针对有轨电车独立轮对与传统轮对的差异，对两者运行时的动力响应进行了对比分析；文献［7］建立了100%低地板与70%低地板有轨电车的轮轨接触模型，研究踏面形式和位置对有轨电车动力响应的影响；文献[8]通过大量轮轨磨耗实测数据对有轨电车轮轨型面匹配问题进行了研究；文献［9］对有轨电车车辆通过曲线时的几何偏移量进行了计算。

然而，学者们在研究中所使用的钢轨大多为普通轨，采用槽型轨的文献较少。文献［10］虽然对比分析了普通钢轨与槽型轨对有轨电车曲线通过时车辆的轮轨动力响应，所得结论也具有一定的参考价值，但其车辆模型较为简易，且只考虑一种曲线工况，文中也没有对车辆曲线通过能力做出评价。文献［11］建立了100%低地板有轨电车模型，分析了该车型下的线路限界和小半径曲线通过能力，但其曲线半径设置过小，实际线路设计时难以实现，且文中未考虑槽型轨的影响。由此可见，在考虑不同钢轨类型影响下有轨电车小半径曲线的通过能力还有待进一步研究。

本文首先利用多体动力学软件SIMPACK建立四模块单车型低地板现代有轨电车仿真模型，分别根据车轮与CHN60钢轨和60R2槽型轨的接触状态，建立了2种轮轨接触模型，并将其引入现代有轨电车模型之中。然后依据规范设置了3种小半径曲线线路，以车辆脱轨系数和轮重减载率为评价指标，对现代有轨电车的曲线通过性能进行评价分析，最后在现代有轨电车钢轨选型与曲线线路设计上给出相应建议，以期对我国现代有轨电车的发展提供参考。

1 现代有轨电车仿真计算模型

计算模型建立时，考虑到现代有轨电车系统的复杂性及计算效率与精度的要求，需要对一些次要因素进行简化；而对系统影响较大的主要因素，尽可能使其符合实际情况。本文在建立车辆模型时有如下几点假设：

（1）整个车辆系统包括多个物体，在模型中将弹性相对很小的物体看做刚体，忽略其弹性变形。

（2）轮对、转向架、车体、悬挂弹簧等均为对称结构。

（3）不考虑钢轨的弹性变形。在高频激励下，轨道的弹性变形对车辆系统有较大影响，但由于现代有轨电车运行速度较低，致使其轮轨激励的低频成分较多，因此本文将钢轨视为刚体，忽略其弹性变形。

（4）车体质量按超员情况进行设置。为模拟车辆实际载客情况，车体质量除考虑自身质量外，还增加了车辆超员运行时乘客的质量。乘客质量依据DG/TJ 08-2213—2016《有轨电车工程设计规范》（以下简称 DG/TJ 08-2213—2016）进行设置［12］。

基于上述假设，将现代有轨电车考虑为多刚体、多自由度的系统，从而建立车辆仿真计算模型，如图1所示。

图1 现代有轨电车仿真计算模型

1.1 车辆模型

在每节车辆中部正下方设有转向架，故单节车辆模型可拆分成主模型与转向架子模型。两个模型间通过改变虚体的铰接位置实现车辆整体模型的建立，如图2所示。车辆建模基本参数取自文献［2］的参数。在计算模型中除轮对外各物体具有6个方向自由度（6 DOF），把轮轨接触考虑为刚性接触，故轮对在沉浮与侧滚两个方向没有自由度（0 DOF），因此单节现代有轨电车共选取20个自由度，如表1所示。

图2 单节车辆拓扑图

表1 单节车辆自由度选取

现代有轨电车全车由4个模块即4节车组成，其中2节车为1组，整列车共2组，车体与车体间通过铰接装置实现4节车辆编组挂接，如图3所示。图中1、2车为一组，3、4车为一组，在头车与尾车设置司机室。参考现代有轨电车铰接装置的实际设置情况，在单节车辆模型之间通过6个铰接实现整车模型的建立；每节车辆之间上、下铰接各一个，且全部设置在铰接区域的中间位置，上部铰接为转动铰，下部铰接为固定铰。建模时，采用x、y、z三个位移方向的大刚度弹簧阻尼力元模拟固定铰，以限制车体下部在这三个方向的相对位移；采用x、y方向的大刚度弹簧阻尼力元模拟1、2车与3、4车之间的转动铰，以传递上部车体间的纵向力，并限制其在x、y向的相对位移；2、3车之间的转动铰采用x方向的大刚度弹簧力元模拟，以传递纵向力，且保证2组车能在上部区域3个方向上有相对运动。

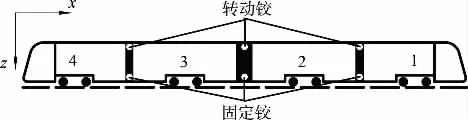
图3 现代有轨电车编组与铰接图示

1.2 轮轨接触模型

本文轮轨接触采用刚性接触方式，即认为车轮与钢轨始终保持接触状态。车轮踏面采用低地板现代有轨电车车轮的踏面外形，钢轨型面为CHN60钢轨与60R2槽型钢轨的型面，建立轮轨刚性接触模型，如图4所示。

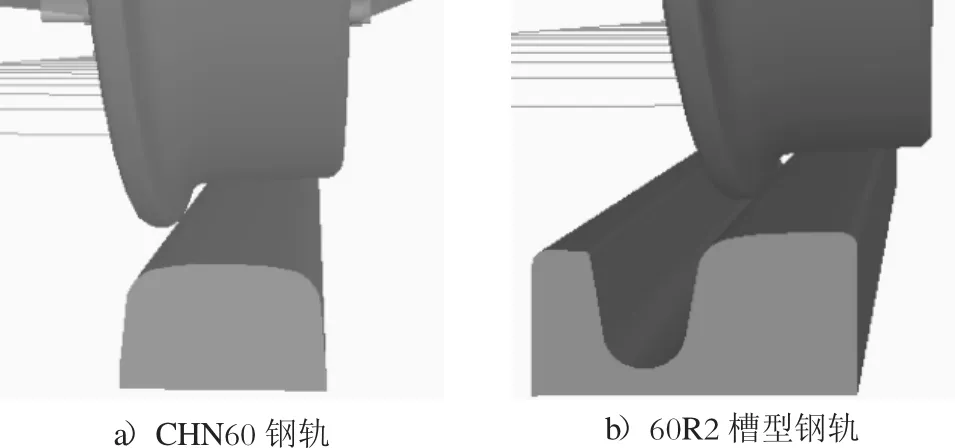
图4 轮轨接触模型

由弹性理论可知，轮轨接触时接触面为椭圆，其长短轴之半ɑ、b由Herz理论确定：

式中，参数 m、n、A、B、k1、k2应根据钢轨、车轮的几何及弹性参数确定。

接触点确定后可求解轮轨作用力。轮轨间法向力用Herz理论计算，假定轮轨间压缩量为p（N），可得法向轮轨力N为：式中，p（1）为单位法向力所产生的弹性压缩量，可由式（4）计算得到：

式中：

E——杨氏模量；

ν——材料泊松比；

φ——变化的角度。

蠕滑力采用FASTSIM算法求得：

式中：

Tx，Ty——分别为纵向、横向蠕滑力；

Mz——绕竖向自旋力；

vx，vy——分别为纵向、横向蠕滑率；

vsp——自旋蠕滑率；

G——剪切模量；

C11，C22，C23，C33——Kaller蠕滑系数。

2 非线性运动稳定性分析

车辆非线性运动稳定性分析一般就是确定车辆的非线性临界速度。它由车辆系统自身结构决定，与线路的激励无关。通过确定现代有轨电车模型的非线性临界速度，可以考察所建模型能否满足车辆实际运行要求，以此初步检验模型的正确性。

计算时先让车辆以较高速度通过一段施加横向不平顺的线路，使其轮对产生一个初始横移量；然后，让车辆在光滑线路上做匀减速运动，当车辆轮对横移量收敛时（即横移量为0），所对应的运行速度即为车辆非线性临界速度。应用该方法对车辆动力学计算模型进行仿真计算，得到车辆前进方向第一组轮对（导向轮对）横移量随速度变化情况如图5所示。

由图5可知：CHN60钢轨上车辆的非线性临界速度为143 km/h，大于60R2槽型钢轨上车辆的非线性临界速度101 km/h。两类钢轨上运行车辆的非线性临界速度均能满足最高运行速度70 km/h的要求，且CHN60钢轨上运行的车辆具有更好的非线性运动稳定性。

图5 车辆非线性临界速度确定

3 小半径曲线线路通过能力分析

曲线线路由不同的几何线形及超高组成，不同的线路设置和外部激扰因素都会影响轮轨相互作用与车辆各部件间的相互作用。车辆曲线通过性能，特别是小半径曲线通过性能，是直接影响车辆运行安全的重要因素。本文针对两种不同钢轨类型下的车辆，依据DG/TJ 08-2213—2016对现代有轨电车平面线路设计的规定与要求，选择3种不同小半径曲线的线路工况，如表2所示。

表2 曲线线路工况

本文以脱轨系数和轮重减载率为指标，对现代有轨电车曲线通过性能进行评价。

车辆在运行过程中，过大的轮轨横向力会使车轮轮缘逐渐爬上轨头而导致脱轨。脱轨系数用于评定该情况是否会发生，可按式（6）计算：

式中：

α——脱轨系数；

Q——轮轨横向力，可由式（5）计算得到；

P——车轮作用于钢轨上的垂向力，由式（3）计算得到。

轮重减载率用于评定车辆在运行过程中是否会因一侧车轮减载过大而导致脱轨，按式（7）计算：

式中：

r——轮重减载率；

ΔP——轮重减载量；

国家标准GB 5599—1985《铁道车辆动力学性能评定和试验鉴定规范》规定：脱轨系数的安全标准值第一限度为1.20，第二限度为1.00（注：第一限度为合格标准，第二限度为增大了安全裕度的标准）；轮重减载率第一限度为0.65，第二限度为0.60。

本文在不同曲线工况下对两种不同钢轨类型上的现代有轨电车车辆进行仿真计算，为更真实地反应实际情况，在轨道上施加美国5级竖向与横向不平顺作为线路激励，得到现代有轨电车导向轮对的安全评定指标最大值（见表3、表4与表5）。图6给出槽型轨车辆导向轮对左轮各工况下安全指标时程曲线。

表3 工况一下评价指标最大值

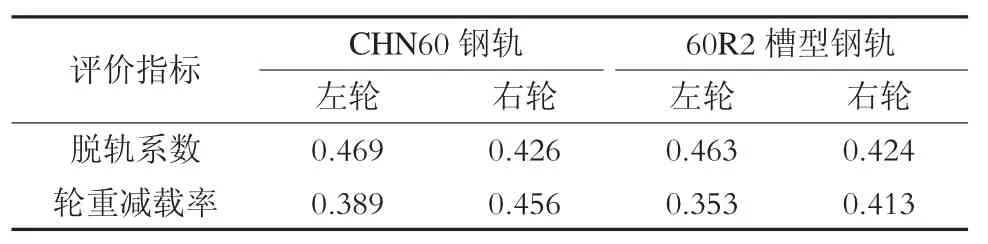
表4 工况二下评价指标最大值

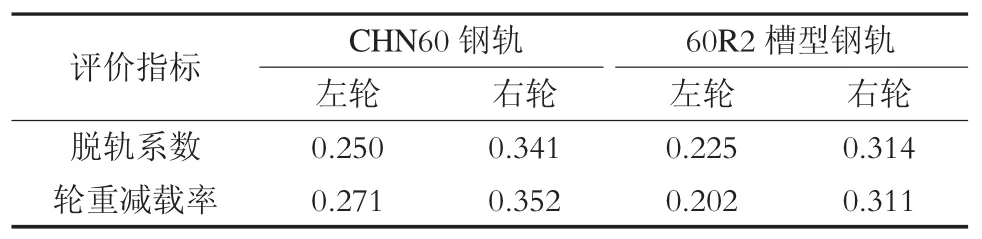
表5 工况三下评价指标最大值

图6 采用槽型轨时车辆导向轮对左轮的评价指标

由表3至表5可知：各工况下行驶在两类钢轨上的现代有轨电车曲线通过性能评价指标最大值均小于对应指标的第二限度值，表明两类钢轨上的现代有轨电车都具有良好的小半径曲线通过能力；工况一下CHN60钢轨上车辆导向轮对左轮的轮重减载率达到0.59，极为接近该安全指标的限制，且随着曲线半径的增大，各安全指标值明显减小（如图6所示），故在实际线路设计时，应尽量避免设置较小半径的曲线线路；两类钢轨上的现代有轨电车在相同工况下各安全指标最大值相差不大，但运行在CHN60钢轨上的车辆各指标最大值均大于槽型钢轨轨上车辆相应指标的最大值，这是由于槽型钢轨断面的特殊形状使其具有一定的护轨功能，因此，在现代有轨电车钢轨选型上，建议使用槽型钢轨。

值得说明的是，目前国内尚无现代有轨电车动力学性能相关的评定标准和线路不平顺数据，文中使用的评定规范和线路不平顺对现代有轨电车的适用性还应进一步商榷。

4 结语

利用多体动力学软件SIMPACK建立了四模块低地板现代有轨电车仿真模型，对不同钢轨类型下现代有轨电车小半径曲线通过性能进行研究，得到以下几点结论：

（1）两类钢轨上的现代有轨电车的非线性临界速度均能满足车辆最高运行速度70 km/h的要求，且CHN60钢轨上运行的车辆具有更好的非线性运动稳定性。

（2）两类钢轨上的现代有轨电车都具有良好的小半径曲线通过能力，但在实际线路设计时，还应尽量避免设置较小半径的曲线线路。

（3）由于槽型钢轨断面的特殊形状，使其具有一定的护轨功能，因而现代有轨电车在小半径曲线线路上运行时，60R2槽型钢轨上运行的车辆具有更好的稳定性，故在现代有轨电车钢轨选型上，建议使用槽型钢轨。

［1］ Transportation Research Board.Track design handbook for light rail transit［R］.Washington,DC：Tcrp Report，2012.

［2］ 吴师.现代有轨电车轨道结构力学分析方法及设计关键技术研究［D］.北京：北京交通大学，2014.

［3］ 陈雷.四模块100%低地板有轨电车动力学性能研究［D］.成都：西南交通大学，2015.

［4］ 罗世辉.大连低地板有轨电车的动力学性能［J］.机车电传动，2001（3）：28.

［5］ 罗世辉.轨道车辆独立车轮的动力学分析［J］.铁道学报，1999（5）：15.

［6］ 李创，孙守光，任尊松.独立车轮转向架车辆曲线通过性能分析［J］.北京交通大学学报，2003，27（5）：86.

［7］ 王明举.低地板轻轨车辆轮轨接触问题的研究［D］.大连：大连交通大学，2008.

［8］ 赵伟，王春艳，张军，等.有轨电车轮轨型面匹配问题的研究［J］.铁道学报，2011，33（2）：34.

［9］ 马威红，沈继强，祝晓波.现代有轨电车车辆通过曲线时的几何偏移量计算［J］.城市轨道交通研究，2015（增 1）：39.

［10］ 陈鹏.槽型轨及普通钢轨对独立轮对轻轨车辆轮轨动力特性的影响［J］.城市轨道交通研究，2012，15（2）：65.

［11］ 吕凤梅，赵建秋，闫晓明，等.100%低地板现代城市有轨电车限界和小曲线通过能力分析［J］.铁道车辆，2013，51（9）：5.

［12］ 上海市城市建设设计研究总院.有轨电车工程设计规范：DG/TJ 08-2213—2016［S］.上海：同济大学出版社，2016：14.

［13］ 中国标准化委员会.铁道车辆动力学性能评定和试验鉴定规范：GB 5599—1985［S］.北京：中国质检出版社，1985：3.