从线性回归到Logistic模型

杨展铭

【摘 要】 线性回归引发了作者对数据分析的思考，原来数学与实际生活的联系如此密切。尽管数学的对象是纯由逻辑混乱和创造力产生的，但在生活中到处都可以发现数学模型对我们的影响。在如今的大数据时代下，对数学的学习带领着我进入一个广阔而又奇妙的世界。

【关 键 词】 线性回归；数学；模型；教学

很多人认为数学是一门严格的一成不变的课程，任何事情都不能脱离事实。人类的大脑不断地创造着数学思想和独立于我们世界的迷人的新世界。某一维中的对象是如何消失在另一维中的，任何两点之间怎么总能找到一个新的点，数是怎样运算的，方程是怎样解出的，坐标如何产生图像，如何用无穷解题，公式如何生成——所有这些似乎都具有一种奇妙的性质。正是这种奇妙和它对智力的挑战让我感受到了数学的趣味，带领着我去不断探究它的魅力。

线性回归模型进行的是输出值的预测问题，那么如果因变量不是连续变量甚至不是数值呢？我查阅了资料后发现广义线性模型中还有一种回归叫作Logistic回归，logistic回归（Logistic regression）与线性回归实际上有很多相同之处，最大的区别就在于他们的因变量不同。logistic回归分析，主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即“是”或“否”，为两分类变量，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。通过logistic回归分析，就可以大致了解到底哪些因素是危险因素。

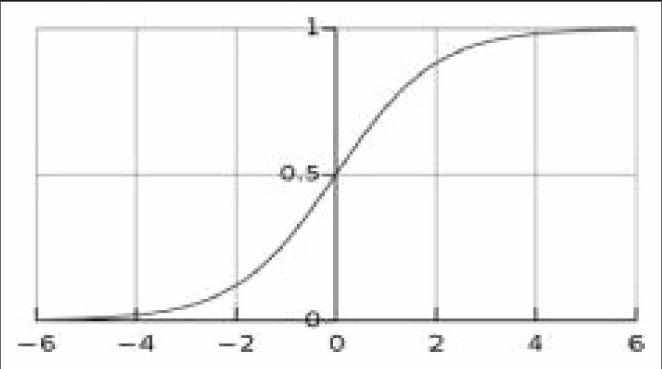
考虑二分类Logistic回归，假设输出标记y属于0或1，而线性回归模型产生的预测值是一个实值，需要将它转化为0或1。在Logistic回归模型中，使用的转化函数是sigmoid函数，如下图所示：

回归的实质是发生概率除以没有发生概率再取对数。就是这个不太烦琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。Logistic回归是直接对分类可能性进行建模，无须事先假设数据分布，这样就避免了假設分布不准确性所带来的问题。

线性回归引发了我对数据分析的思考，原来数学与实际生活的联系如此密切。在如今的大数据时代下，对数学的学习带领着我进入一个广阔而又奇妙的世界。

【参考文献】

[1] 李元章，何春雄. 线性回归模型应用及判别[M]. 广州：华南理工大学出版社，2016.

[2] 威廉·巴里. 线性回归分析基础[M]. 上海：格致出版社，2011.

[3] 姜阿丽. Logistic回归模型原理介绍及实例分析[J]. 福建质量管理，2017（8）.endprint