基于覆盖树的电路网络分析法

李 竹， 黄锦安， 徐行健， 蔡小玲

(南京理工大学 电光院, 江苏 南京 210094)

0 引言

众所周知，在一般的电路分析方法中，割集电压法选择任意一个树的树支电压ut作为独立变量，通过解代数方程求得ut，再由ut求树支电流it和连支电压ul，连支电流il[1]；回路电流法是选择任意一个树的连支电流il作为独立变量，当求得il后，再由il求ul、it和ut。然而在上述方法中所选择的任意树并不能以其连支电压ul或树支电流it为对偶的独立变量进行分析。那么能否寻求一个树，依赖于这个树进行分析时，既可用ut或il作为独立变量，也可用it或ul为独立变量进行求解呢？为此，本文引进了覆盖树的概念，提出了解决上述问题的分析法，并举例进行说明。

1 覆盖树

设有图G的一个树T，设B(T)为T的所有单树支回路的支路构成的集合，Q(T)为T的所有单连支割集的支路构成的集合，若满足B(T)∪Q(T)为图G中的所有支路，则T被称作图G的一个覆盖树。特别地，若B(T)包含图G中所有支路，则T被称作图G的一个B覆盖树；若Q(T)包含图G中所有支路，则T被称作图G的一个Q覆盖树。

现举例说明。在图1所示图G中，选取1，2，3为G的一个树，由树支1，2，3，形成的单树支回路(1，4，7)(2，5，6)(3，6，7)包含了G的所有支路，故T=(1，2，3)为图G的一个B覆盖树。在图2所示图G中，选取1，2，3，4为G的一个树，由于连支5，6，7形成的单连支割集(2，5，3)(6，3，4)(7，2，1)的并集包含了G的所有支路，故T=(1，2，3，4)为图G的一个Q覆盖树。

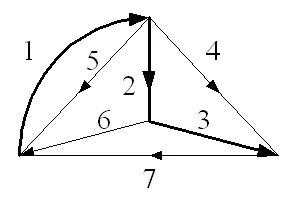
图1 B覆盖树

图2 Q覆盖树

2 基于覆盖树的电路分析

在电路分析中，割集电压法和回路电流法通常是任选图G的一个树T来分析，割集电压法中，当选定以T的树支电压为独立变量时，连支电压是树支电压的线性组合，但是，如果选取连支电压为独立变量，树枝电压并不一定是连支电压的线性组合。回路电流法中，当选定以T的连支电流为独立变量时，树支电流是连支电流的线性组合，但是，如果选取树支电流为独立变量，连支电流并不一定是树支电流的线性组合。也即由于树的任意性不能保证树支电压与连支电压之间，连支电流与树支电流之间互为线性组合。那么能否寻求一种树，依赖于这种树进行分析时能够保证树支电压与连支电压之间、连支电流与树支电流之间互为线性组合呢？下述定理给出了答案。

定理：当且仅当图G的一个树T是B覆盖树时，不仅连支电压是树支电压的线性组合，树支电压也是连支电压的线性组合。当且仅当图G的一个树T是Q覆盖树时，不仅树支电流是连支电流的线性组合，连支电流也是树支电流的线性组合。

证明：必要性：T是G的一个树，在割集电压法和回路电流法中，当选T的树支电压或连支电流为独立变量时，连支电压是树支电流的线性组合，树支电流是连支电流的线性组合。当T是图G的B覆盖树时，B(T)为T的所有单树支回路的支路构成的集合，且覆盖图G，当以连支电压为变量时，T的某个树支电压可由这个单树支回路的其它连支电压线性表示，因而T的各个树支电压都可由各个单树支回路中的连支电压线性表示；当T是图G的Q覆盖树时，Q(T)为T的所有单连支割集的支路的集合，且覆盖图G，当以树支电流为变量时，T的某个连支电流可由这个单连支割集的其它树支电流线性表示，因而T的各个连支电流都可由各个单连支割集中的树支电流线性表示。

充分性：设图G的一个树T不是覆盖树，且T不是B覆盖树，则在图G中至少有两个树支不能形成单树支回路，在与这两个树支关联的回路中，其中任意一个树支电压都不能用这个回路中其它连支电压来线性组合；设图G的一个树T不是覆盖树，且T不是Q覆盖树，则在图G中至少有两个连支不能形成单连支割集，在与这两个连支关联的割集中，其中任意一个连支电流都不能用这个割集中其它树支电流来线性组合；因此，仅当T是B覆盖树或Q覆盖树时，树支电压与连支电压之间，连支电流与树支电流之间才能互为线性组合。

由上述定理可知，当在图G中找出某一个B覆盖树或Q覆盖树时，不仅可用树支电压ut或连支电流il为独立变量进行求解，而且也可用连支电压ul或树支电流it为独立变量进行求解。显然，这两种分析中存在着一定的联系。我们把这种方法称为基于覆盖树的电路网络分析法，并在下面举例说明。

3 举例说明

例1. 图3为电路所对应的图G。

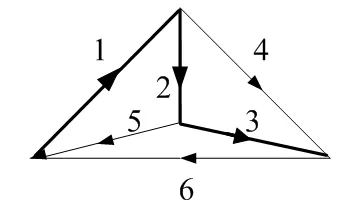
图3

在图G中, 选B覆盖树T=(1，2，3)。由单连支回路可得基本回路矩阵Bf(下述矩阵中列序均为先树支后连支)：

Bf={Bt1l}= 1 2 3 4 5 6

由BfU=[Bt1l][UtUl]T得：

Ul=-BtUt

(1)

由单树支回路可得回路矩阵

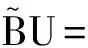
(2)

其中Ut，Ul为树支电压列向量和连支电压列向量，U为支路电压列向量。由式(1)和(2)可见连支电压Ul与树支电压Ut互为线性组合。

在正向分析中，以连支电流为变量可得如下回路电流方程

BfZBfTIl=BfUs-BfZIs

(3)

式中，Bf为基本回路矩阵，Z为支路阻抗矩阵，Il为连支电流列向量，US为支路电压源列向量，IS为支路电流源列向量。

按本文所提方法，也可以用连支电压为变量进行分析。由式(2)可知支路电压列向量U可表示为

(4)

又QfI=0

(5)

式中，Qf为基本割集矩阵，I为支路电流列向量。支路方程可表示为

I=Y(U+Us)-Is

(6)

式中，Y为支路导纳矩阵。由式(4)、(5)和(6)可得以连支电压为变量的如下电压方程。

(7)

式(7)即为以连支电压Ul为变量的方程，可直接解得Ul。

由上述分析可知，只要找到图G的B覆盖树，不仅可用连支电流Il为独立变量进行分析，也可用连支电压Ul为独立变量进行分析。式(3)和(7)可直接作为公式使用。

例2． 图4为电路所对应的图G。在图G中, 选Q覆盖树T=(1,2,3,4)。由单树支割集可得基本割集矩阵。

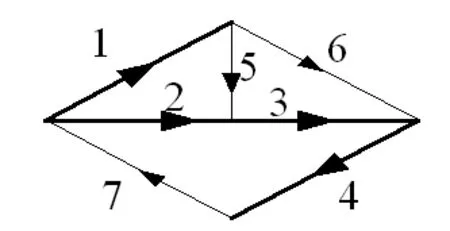
图4

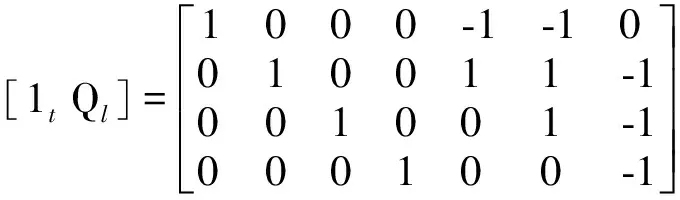
由QfI=[1tQl][ItIl]T=0,得

It=-QlIl

(8)

由单连支割集可得割集矩阵

(9)

由式(8)和(9)可见树支电流It与连支电流Il互为线性组合。

在正向分析中，以树支电压为变量可得如下割集电压方程

(10)

我们也可以It为变量进行分析。 由式(9)可知各支路电流与树支电流It之间的关系：

(11)

又BfU=0

(12)

且支路方程：

U=Z(I+Is)-Us

(13)

其中Bf为基本回路矩阵，Z为支路阻抗矩阵，US为支路电压源电压列向量，IS为支路电流源电流列向量。由式(11)、(12)和(13)可得方程：

(14)

式(14)即为以It为变量的方程，可直接解得It。

由上面分析可知，只要找到图G的Q复盖树，即可以树支电压Ut为独立变量分析，也可用树支电流It为独立变量进行求解。式(10)和(14)可直接作为公式使用。

4 结语

本文引进了覆盖树的概念，使树支电压和连支电压、连支电流和树支电流能够互为线性组合。本文提出的基于覆盖数的电路网络分析法，使得树支上的电压和电流、连支上的电流和电压均可作为独立变量进行分析求解。这种分析方法将使电路分析变得更加灵活简便。(李 竹等文)

[1] 邱关源. 电路(第5版). 北京：高等教育出版社.2003.