LA-ICP-MS锆石U-Pb同位素定年存在的基体效应研究进展

, ,

(天津地质矿产研究所, 天津 300170)

锆石(ZrSiO4)具有封闭温度高、稳定性好、普通铅含量低等特点,一直是U-Pb同位素定年的首选对象。目前最常采用的锆石U-Pb同位素定年方法有同位素稀释热电离质谱法(ID-TIMS)、二次离子探针质谱法(SIMS)和激光剥蚀电感耦合等离子体质谱法(LA-ICP-MS)。

自20世纪80年代,GRAY等[1]开创了激光和电感耦合等离子体质谱联用技术以来,LA-ICP-MS以其原位、实时、快速、高分辨率、高灵敏度、可同时测定元素含量及同位素比值等特点,在锆石微区原位U-Pb同位素定年研究中发挥了非常重要的作用[2-7]。

然而,与ID-TIMS相比,LA-ICP-MS锆石U-Pb定年结果的准确度和精密度被限定在约4%的水平,与高精准的ID-TIMS(约0.1%)相比仍存在相当大的差距,这在很大程度上影响了该方法定年结果的可靠性[6,8-11]。

影响LA-ICP-MS锆石U-Pb定年结果准确度和精密度的因素有很多,包括激光条件(波长、脉冲时间、能量等)、样品池设计、采样策略(束斑大小、剥蚀方式等)、气流设置(载气、辅助气)、ICP调谐、数据处理方案等[12-19]。SYLVESTER[20]对这些因素进行了深入的研究,在作用机理和解决方案等方面取得了重要的进展,并将关键性研究进展进行了较为系统的总结评述。

在LA-ICP-MS锆石U-Pb定年研究中,国内外研究学者普遍采用与样品“基体匹配”(化学组成和物理形态相近)的外部标准锆石进行校正,从而消除基体效应。然而,采用同种矿物作为外标的方法是否真的消除了基体差异引起的基体效应？如果没有,那么采用基体匹配的外标校正方法还存在多大的基体效应,是否对U-Pb定年结果的准确度和精密度产生影响？

近年来,越来越多的研究提出基体效应是影响LA-ICP-MS锆石U-Pb定年结果准确度和精密度的重要因素,并在基体效应产生的机理和应对策略等方面取得了较为一致的认识[8-9,21-25]。本文旨在对前人有关LA-ICP-MS锆石U-Pb存在的基体效应的研究进行总结,并结合自身经验和理解对其加以评述。

1 基体效应的定义

大量有关LA-ICP-MS的文献都谈及基体效应(通常与元素、同位素分馏并提),但对基体效应的定义有明确说明的文献并不多见。

李冰等[26]认为基体效应,即非质谱干扰,分为高盐溶液引起的物理效应和基体对分析物的抑制或增强效应。

SYLVESTER[20]指出当某种分析技术的测定结果取决于分析对象的化学成分或物理性质时,则认为该技术存在基体效应。若测定结果只能采用与样品的“基体匹配”的外部标准物质进行标准化予以校正,则该技术“遭受”基体效应的干扰。

PETERMAN等[27]指出微束技术(LA-ICP-MS、SIMS)在测定时提取了分析对象(标准锆石和样品锆石)的基体(包括Zr、Si、P、Ca、REE等),由于被提取物质的蒸发、活化等性能存在差异,从而产生元素分馏和同位素分馏,这种现象被称为基体效应。

SYLVESTER[20]和PETERMAN等[27]定义的基体效应实际上与李冰等[26]定义的第二种类型的基体效应在本质上是一致的。高盐溶液引起的物理效应主要是溶液ICP-MS分析技术存在的基体效应,而在“干等离子体”条件的LA-ICP-MS分析技术中,通常认为不存在这种类型的基体效应。

对于LA-ICP-MS锆石U-Pb定年而言,基体效应是指由于标准锆石和样品锆石基体在化学组成和(或)物理性质上的差异,使得二者在分析过程中元素和同位素分馏行为不一致,从而导致外标校正技术获得的U-Pb定年结果准确度和精密度降低的一种现象。

2 基体效应的类型

2．1 元素基体效应

元素基体效应首先由BLACK等[22]发现,该研究采用LA-ICP-MS对5种标准锆石(TEMORA 1、QGNG、TEMORA 2、R33、AS3)进行定年,其206Pb/238U表面年龄与“真实年龄”(ID-TIMS206Pb/238U表面年龄)存在差距(以下统称206Pb/238U年龄差)。206Pb/238U年龄差可高达约±3.0%,明显高于分析精度(约0.5%),见图1(矩形框的长度反映206Pb/238U年龄差的2倍标准差,TEMORA 1被用作外部校正标准,其206Pb/238U年龄差设定为0,其不确定度反映TIMS206Pb/238U表面年龄的2倍标准差)。经其研究发现,206Pb/238U年龄差是由一种与锆石中多种元素含量相关的基体效应所致。这种基体效应是因锆石化学成分差异(REE+Y,P)导致,本质上可能受控于“磷亿矿”元素取代机制以及相关的晶格畸变,因此将其称为元素基体效应。

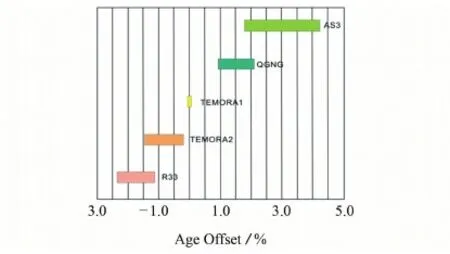
图1 5种标准锆石LA-ICP-MS 206Pb/238U年龄差[22]Fig. 1 206Pb/238U age offsets derived by LA-ICP-MS analysis for five zircons standard[22]

BLACK[22]指出如果不对元素基体效应进行校正,锆石LA-ICP-MS206Pb/238U定年结果的准确度将不优于±3.0%。于是,该研究考察了多种元素(U、Th、P、Hf、La、Ce、Nd、Sm、Eu、Dy、Lu)与206Pb/238U年龄差之间的相关性。结果显示:10种元素与年龄差之间的相关性差异很大(见表1),其中U、Th、P、Sm、Nd与年龄差的相关性良好。虽然U、Th与年龄差的相关系数较高,但二者测定误差较大,不能构建有价值的校正方程。P、Sm、Nd与年龄差之间具有强烈的线性正相关,见图2[注:误差椭圆代表平均值的2倍标准误差(±2 SE),年龄差的不确定度由LA-ICP-MS206Pb/238U年龄传递,忽略ID-TIMS年龄的不确定度,虚线表示最佳拟合曲线],P、Sm与年龄差构建的回归方程的加权平均方差(MSWD)过高,而Nd与年龄差能够提供良好的回归方程Offset(%)=(1.17±0.5)wNd(μg·g-1)+(-3.8±1.8)(MSWD=2.0)。利用该方程,可以建立LA-ICP-MS元素基体效应的定量校正方程:206Pb/238Ucorrected age=(206Pb/238Umeasured age)×(1-c/100),其中c=(-0.277±0.095)×wNd(μg·g-1)+(0.90±0.30)-Offset(%)。研究者可以在LA-ICP-MS U-Pb分析时,检测Nd+信号强度,基于这一方程对元素基体效应进行校正。

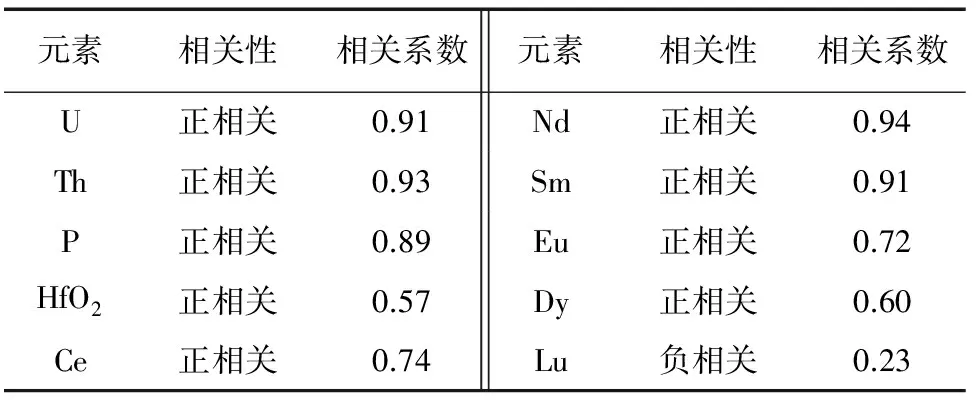
表1 锆石中代表性痕量元素与206Pb/238U年龄差之间的相关性参数[22]Tab. 1 Correlation parameters between the representative trace elements in zircon and LA-ICP-MS 206Pb/238U age offsets[22]

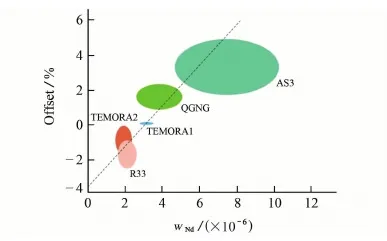
图2 锆石中Nd含量与206Pb/238U年龄差之间的线性关系[22]Fig. 2 Linear relationship between Nd concentration in zircon and the 206Pb/238U age offsets[22]

BARLING等[28]采用MC-ICP-MS进行Pb同位素分析时,发现分析样品的基体成分如Ca、Al、Fe、Mg等元素会导致Ar等离子体电荷密度降低(ArAr+/Ar2+升高),使进入离子束中心区的Pb+和Tl+比例增大,从而导致基于质量歧视校正的Pb同位素比值产生偏畸(-150～200 μg·g-1·amu-1)。基于此,KLTZLI等[9]认为导致LA-ICP-MS锆石U-Pb分析结果存在的元素/同位素比值漂移很可能与影响等离子条件的因素有关,如Ca、Al、Fe、Mg等元素有关的基体效应导致的信号不同程度增强(或抑制),以及被剥蚀物质的气溶胶颗粒大小分布。

ALLEN等[23]同样发现了明显的206Pb/238U年龄差(-5%～3%),测定了6种标准锆石的ZrO2、HfO2、P、Ti、Y、La、Ce、Sm、Eu、Dy、Lu、U含量，并利用同位素比值推算出Th/U、放射成因Pb,将这些参数与206Pb/238U年龄差作相关性检验。结果表明:206Pb/238U年龄差与放射成因Pb总量、锆石的α通量都呈现良好的相关性,而与其他12种元素(包括典型的REEs)以及Th/U的相关性都很差(R2≤0.46)。由此推断产生年龄差的原因不是与锆石中一种或者多种元素有关的基体效应,而与锆石所遭受的辐射损伤密切相关,即α通量基体效应。

2．2 α通量基体效应

ALLEN等[23]的研究表明:标准锆石的206Pb/238U年龄差高达3%;而对于年轻的锆石样品,基体效应更严重,通常会导致-5%的年龄差。同时该研究发现206Pb/238U年龄差与放射成因Pb和α通量呈很好的相关性。放射成因Pb是锆石中U、Th衰变的产物,而α通量正是表征锆石遭受的辐射损伤程度的参数。采用LA-ICP-MS对发生辐射损伤的锆石进行剥蚀时,紧邻剥蚀坑的区域内的Pb比U更容易逸出,从而导致206Pb/238U表面年龄偏高。锆石的辐射损伤程度越高,其206Pb/238U比值偏高的幅度就越大。

因此,ALLEN等[23]认为引起LA-ICP-MS锆石206Pb/238U年龄差的最可能因素是标准锆石与未知锆石之间物理性能(晶体状态)的差异,这种差异本质上由二者遭受的α通量不同所致。未知锆石的LA-ICP-MS206Pb/238U年龄比“真实年龄”(TIMS U-Pb年龄)偏低还是偏高取决于标准锆石与未知锆石哪个经历了更高的α通量。该研究指出在没有精确的TIMS或者40Ar-39Ar定年结果进行比对的前提下,α通量基体效应很容易被研究者忽视。然而该效应对于年轻锆石定年结果的影响通常非常显著,这是因为年轻锆石累积的α通量一般远低于标准锆石。该效应对于古老锆石(大于1.0 Ga)的影响并不明显,这是因为研究者通常采用古老锆石的207Pb/206Pb表面年龄作为结晶年龄,而α通量基体效应主要影响Pb/U比值,而不影响Pb/Pb比值。即便如此,这一基体效应对古老锆石206Pb/238U表面年龄的影响依然会关系到锆石年龄谐和度的计算(用于考察207Pb/206Pb年龄的可信度)。

ALLEN等[23]利用13种锆石的206Pb/238U年龄差与α通量建立的对数-线性关系(y=407.89e0.846x,见图3)似乎可以被用来校正α通量基体效应。然而图3中α通量(Dα)是采用公式(1)计算的理论α通量,它是假设锆石自形成后一直记录U、Th衰变对晶体造成的损伤且没有受到后期热事件的影响。

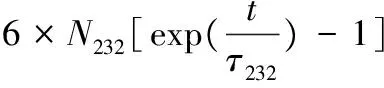
式中:N238、N235、N232分别为每克锆石含有的238U、235U、232Th的原子数目;τ238、τ235、τ232为对应的半衰期;t代表地质年龄。

理论α通量与锆石实际的蜕晶化程度通常并不完全对应,这是因为锆石的辐射损伤会在环境温度高于其自退火温度时进行修复而不保留其间产生甚至以前累积的α通量[29-30]。研究表明,锆石长期深埋地壳的自退火温度为(250±50) ℃,明显低于锆石的U-Pb封闭温度(750±100) ℃[30-36]。可见,锆石U-Pb体系封闭状态与α通量保存状态并不一致。例如,锆石自结晶开始至环境温度降至退火温度以下时,锆石才开始累积α通量,对于深成岩而言,锆石开始累积α通量的时间可能会明显晚于其206Pb/238U年龄。又如,若锆石自形成后经历了中低温变质,虽然其U-Pb体系可能保持封闭,而α通量却已被退火修复。因此,按照锆石的U、Th含量及其年龄计算的Dα很可能与锆石实际保留的Dα存在较大差距。

由于很难确定锆石是否经历了自退火事件以及退火修复的程度,导致很难准确获得锆石内部实际保存的α通量。因此,图3所建立的关系式不能够被用来校正α通量基体效应。不仅如此,α通量基体效应的大小还与剥蚀方式有关。KLTZLI等[9]采用线扫描进行激光剥蚀得到的206Pb/238U年龄差与α通量之间的关系式[见图4(假设斯里兰卡锆石仅保存了55%的理论α通量。VC#1-2的数据明显异常,其余数据点则拟合了良好的指数关系)]与ALLEN等[23]对应的关系式具有明显差别。对比图3和图4可以看出,采用线扫描方式进行锆石U-Pb定年分析在一定程度上减轻了α通量基体效应。

图3 13种标准锆石的LA-ICP-MS 206Pb/238U年龄差 与α通量的线性关系[23]Fig. 3 Linear relationship between LA-ICP-MS 206Pb/238U offsets and alpha doses for the 13 standard zircons[23]

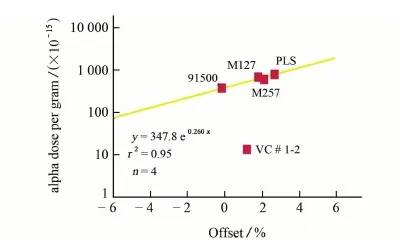
图4 LA-ICP-MS 206Pb/238U年龄差与 计算的α通量的线性关系[9]Fig. 4 Linear relationship between LA-ICP-MS 206Pb/238U offsets and calculated alpha doses[9]

2．3 高铀或高Ddpa基体效应

高铀基体效应,通常发生在高铀锆石SIMS206Pb/238U定年分析中,当锆石的铀含量超过一定临界值,206Pb/238U表面年龄与锆石的铀含量呈现出强烈的正相关。

高铀基体效应首先被WILLIAMS等[21]发现,该研究采用SHRIMP对Tasmanian辉绿岩中锆石进行定年研究时发现:当锆石中U的质量比在0～2 500 μg·g-1时,其206Pb/238U表面年龄是一致的;当U的质量比高于2 500 μg·g-1时,其表面年龄以约3%/(1 000 μg·g-1)的速率增长。

许多SIMS206Pb/238U定年研究相继报道了高铀基体效应,但目前对产生这种效应的铀含量临界值尚未达成统一认识(2 500 μg·g-1[37],4 000 μg·g-1[38],3 000 μg·g-1[24]),表面年龄的增长速率也不相同[3%/(1 000 μg·g-1)[21],2%/(1 000 μg·g-1)[37],2.2%/(1 000 μg·g-1)[24],0～8.5%/(1 000 μg·g-1)[39]]。这种差异被解释为高铀基体效应受仪器条件(质谱类型、质谱参数)和样品性质(锆石蜕晶化程度)共同影响[37,39]。

WHITE等[39]在不同的参数条件下,利用SHRIMP RG对Tasmanian辉绿岩中锆石进行定年,结果表明:锆石4个阶段的SHRIMP RG206Pb/238U年龄与U的质量比具有明显的相关性(相关系数大于0.8),Pb/U比值的增大速率最高为8.5%/(1 000 μg·g-1),最低为2.1%/(1 000 μg·g-1),并且都不存在低铀区域的坪区年龄。采用SHRIMP RG、SHRIMP I、SHRIMPII等3种二次离子质谱(具有不同的二次离子提取系统)对Mount Dromedary二长岩、Tasmanian辉绿岩中锆石进行定年,结果显示两种锆石的SHRIMPI、SHRIMP II的206Pb/238U年龄与U的质量比之间相关性低,Mount Dromedary二长岩锆石的SHRIMP RG测试结果比Tasmanian辉绿岩锆石测试结果表现出较低的相关性。

WHITE等[39]的研究不仅详细研究了仪器类型及参数条件对高铀基体效应的影响,而且指出锆石的辐射损伤随时间逐渐累积,对于年轻的锆石,即使U的质量比高于10 000 μg·g-1也不显示出高铀基体效应。这说明要定义高铀锆石,还需要考虑锆石自身的年龄。因此,高铀基体效应的临界值应当随着年龄的增大而减小。对于古老的锆石(大于4 Ga),即使U、Th等放射性元素含量非常低,但其在漫长的地质年代中遭受相当强烈的辐射损伤。可见,只有当锆石遭受的辐射损伤积累到一定程度,其U-Pb定年结果才显现出高铀基体效应,因此不能以统一的铀含量临界值来衡量所有锆石分析存在的高铀基体效应。

GAO等[24]指出相比“铀含量”,锆石的“辐射损伤程度(Ddpa)”更适合描述高铀基体效应,并将其称之为“高Ddpa基体效应”。Ddpa是为便于比较天然锆石和人工试验锆石(如离子辐照、Pu掺杂)的辐射通量而提出的,代表每克锆石发生离位的原子总数(见公式2),它与Dα所代表的物理意义是相同的,都是反映锆石晶格遭受的辐射通量[35,41]。GAO等[24]将所有测得的Ddpa与206Pb/238U年龄作图发现:当Ddpa≤0.08时,锆石U-Pb年龄不随Ddpa变化而改变;当Ddpa>0.08时,U-Pb表面年龄与Ddpa呈现出强烈的正相关。这说明Ddpa>0.08的锆石受到强烈的辐射损伤导致其定年结果受到基体效应的明显影响。

Ddpa≈9.40×105×Dα×M/(NA×6)(2)

式中:NA为阿伏伽德罗常数;M为锆石的相对分子质量;Dα为α通量[41]。

高铀基体效应一直被局限在高铀锆石(铀质量比高于n×1 000 μg·g-1)的定年研究中,而GAO等[24]提出的高Ddpa基体效应,将高铀基体效应的研究拓宽至辐射损伤超过临界值(0.08)的所有锆石,这意味着在研究铀含量低却古老的锆石时也很可能存在高Ddpa基体效应。然而,如前所述,由于后期高温退火自修复作用的影响,很难准确获得锆石实际保留的α通量(Dα),因此要获得准确的Ddpa同样困难。越老的锆石其Dα和Ddpa越复杂,因为晶格的缺陷会引入氢氧化物,而且痕量水的存在会促进热退火进程,导致锆石保留的辐射损伤远低于计算得到的Dα和Ddpa[31,41-42]。

LA-ICP-MS研究者一度认为该技术并不存在高铀或高Ddpa基体效应[43-45]。例如,ZHAO等[45]采用SHIRIMP和LA-ICP-MS对豆乍山花岗岩锆石进行U-Pb定年分析,结果表明:SHIRIMP206Pb/238U年龄与铀含量之间呈现明显的线性正相关,存在明显的高铀基体效应(没有临界值),206Pb/238U年龄分布范围很宽(幔部,198～233 Ma;边部,260～295 Ma)。而LA-ICP-MS206Pb/238U年龄与铀含量之间不存在相关性,高铀(12 840～26 018 μg·g-1)和低铀(1 215～4 075 μg·g-1)锆石(域)年龄一致,206Pb/238U年龄分布范围很窄(幔部,196～208 Ma;边部,196～212 Ma)。据此,该研究认为SHRIMP分析高铀锆石并不能给出可靠的U-Pb年龄,LA-ICP-MS由于不存在高铀基体效应,所以能够准确对高铀锆石进行U-Pb定年。

从数据质量的角度考虑,ZHAO等[45]研究的LA-ICP-MS Pb/U比值误差椭圆相对分散(见图5),过高的MSWD值(13)降低了206Pb/238U年龄加权平均值的可信度。ZHAO等[45]解释MSWD值过高是由于单点分析的内部精度较小(约1%)所致,当选用外部精度(约2.5%)时,MSWD值由13降为1.4。这种解释与KLTZLI等[9]提出的LA-ICP-MS锆石U-Pb定年分析结果的不确定度不小于3%的观点一致。而这个观点是基于锆石中Ca、Al、Fe、Mg有关的基体效应提出的,并且该研究的基体效应也被认为很可能是α通量基体效应。

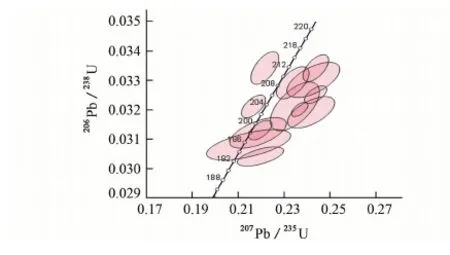
图5 豆乍山花岗岩锆石LA-ICP-MS U-Pb数据谐和图[45]Fig. 5 Concordia diagram of LA-ICP-MS U-Pb dating results of zircons from the Douzhashan granite[45]

随着LA-ICP-MS基体效应有关研究的不断深入[9,22-23],研究者已经开始意识到在LA-ICP-MS锆石U-Pb定年时也存在着与锆石辐射损伤有关的基体效应,即α通量基体效应。α通量基体效应与高Ddpa基体效应本质上反映的是同一个问题,即晶格损伤的程度不一致导致标准锆石和未知锆石物理性能的差异,从而使得外部标准校正方法出现系统误差(即206Pb/238U年龄差,甚至包括207Pb/235U及207Pb/206Pb年龄差)。虽然二者本质相同,但是其研究对象却有很大差异。高Ddpa基体效应是针对高铀锆石U-Pb定年提出的一种基体效应,其目的在于寻找一个统一的临界值来限定是否存在该效应。α通量基体效应则是针对所有具有不同辐射损伤(α通量)的锆石(包括高铀锆石、低铀锆石)提出的一种基体效应,其目的在于消除LA-ICP-MS锆石U-Pb定年的系统误差。显然,α通量基体效应比高Ddpa基体效应更具有普遍意义,更适合描述微束技术(SIMS和LA-ICP-MS)锆石U-Pb定年中辐射损伤差异所致的系统误差。

3 基体效应的应对策略

LA-ICP-MS锆石U-Pb定年是否存在元素基体效应尚存在较大争议。目前为止,BLACK等[22]发现的(REE+Y,P)元素基体效应还没有被其他研究证实。与ALLEN等[23]研究采用的6种标准锆石相比,BLACK等[22]选取的5种标准锆石年龄范围很窄,其中低于1.0 Ga的3种标准锆石TEMORA 1、TEMORA 2、R33的TIMS206Pb/238U年龄分别为(416.75±0.24) Ma,(416.78±0.33) Ma,(419.26±0.39) Ma,年龄跨度不足3 Ma;而QGNG和AS3的TIMS206Pb/238U年龄分别为(1842.0±3.1) Ma和(1 099.0±0.7) Ma。由于二者年龄大于1.0 Ga,其206Pb/238U年龄误差较大,通常选用207Pb/206Pb年龄作为结晶年龄,因此QGNG和AS3对于元素基体效应研究的意义有限。然而元素基体效应对于年轻锆石(小于1 000 Ma)的定年结果影响非常重要,BLACK等[22]选用的3种年轻锆石的年龄近乎一致,且U、Th、P、Sm、Nd等元素分布范围也很窄,若在相关性研究中去掉大于1.0 Ga的QGNG和AS3,剩余3种锆石的数据点将会集中分布,甚至重合(见图6)。且由于被用作外部标准,TEMORA 1的206Pb/238U年龄差被设定为零,与LA-ICP-MS测定无关。显然,BLACK等[22]研究得到的Nd元素与206Pb/238U年龄差之间的相关关系值得商榷。

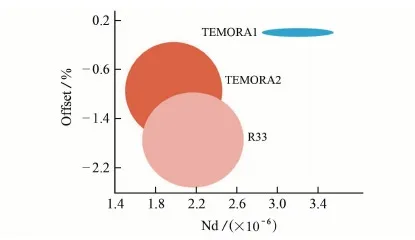
图6 年轻标准锆石(小于1.0 Ga)中Nd含量与206Pb/238U表面 年龄差之间的相关性[22]Fig. 6 Correlation between Nd concentration and the 206Pb/238U age offsets of the young standard zircons (<1.0 Ga)[22]

高铀基体效应受到仪器条件和样品性质的共同影响,其本质上是一种高Ddpa基体效应。

GAO等[24]研究建立了避免高Ddpa基体效应影响的U-Pb数据筛选指标。考虑到退火修复对Ddpa的影响,该研究提出拉曼光谱分析锆石结晶状态与Ddpa>0.08的筛选指标相结合的方法,完成对锆石U-Pb数据的取舍。然而由于Ddpa采用的是公式(2)计算的理论Ddpa,很可能会误将“实际Ddpa<0.08<理论Ddpa”的锆石筛除,从而丢失该类锆石所携带的年龄信息及其蕴含的地质意义。更重要的是,这种筛选方法并不适合以下两类样品的分析:① 锆石含量低的高铀岩石样品;② 岩石样品的锆石含量虽高,但是缺少低Ddpa或低Dα锆石。另外,该研究忽视了质谱类型、质谱参数对高Ddpa基体效应的影响。因此,Ddpa>0.08的筛选指标是否适用于所有锆石有待进一步考察。

α通量基体效应本质上是因标准锆石和未知锆石晶格损伤程度(即α通量)不同所致。自退火修复作用的存在导致要准确获得锆石实际保存的α通量非常困难。虽然可以运用已建立的经验方程(公式3)[31]计算锆石实际保存的α通量。然而,这一方程的应用仅限定在FWHM<10 cm-1且Dα<2×1018g-1的范围[46]。

FWHM(cm-1)≈1.2+1 400×

Dα(1015/mg,preserved)(3)

式中:FWHM为锆石B1g模半高宽(1 008 cm-1),Dα为锆石实际保存的α通量。

ALLEN等[23]提出在进行LA-ICP-MS U-Pb定年分析前,通过高温退火试验,修复标准锆石和未知锆石的晶格损伤,消除二者α通量的差异,可以有效地避免α通量基体效应。该研究在850 ℃下对6种标准锆石退火数小时后采用相同的激光剥蚀条件(质谱仪由安捷伦7500S更新为安捷伦7700)进行定年,结果显示退火锆石的206Pb/238U年龄基本都在误差范围内与真实年龄(TIMS年龄)一致,锆石的206Pb/238U年龄差均小于或等于外部标准锆石TEMORA 3的内部精度(0.52%),而且年龄差与α通量之间不具有相关性(见图7)。

图7 退火后的6种标准锆石的LA-ICP-MS 206Pb/238U 年龄差与α通量之间的关系[23]Fig. 7 Correlation between 206Pb/238U offsets and alpha doses for the six standard zircons[23]

然而,ALLEN等[23]的研究尚存在以下不足:① 在验证年龄差与锆石α通量的相关性时,该研究在6种标准锆石的基础上增加了7种锆石样品的数据,13种锆石的年龄差与锆石α通量相关性非常好。然而当去除7种锆石样品的数据后,6种标准锆石的α通量与年龄差之间的相关性就大幅降低(r2=0.75,见图8)。这说明锆石种类的增加(尤其是年龄范围和U、Th元素含量范围的拓宽)使得年龄差与锆石α通量之间的相关性变得明显。因此,在考察年龄差与元素(尤其是微量元素)的相关性时是否也应通过增加锆石的种类(拓宽年龄、元素含量范围)作更深入的检查？② 退火前后的两次循环试验采用的激光器及其试验参数虽然一致,但采用的质谱由之前的安捷伦7500S更换为安捷伦7700,仪器条件的变更对试验结果比对的影响是否可以忽视？该研究并未对此进行详解。

图8 未退火的6种标准锆石的LA-ICP-MS 206Pb/238U 年龄差与α通量之间的相关性[23]Fig. 8 Correlation between 206Pb/238U offsets and alpha doses for the six un-annealed standard zircons[23]

与建立基体效应校正方程和Pb/U数据的筛选指标的方法相比,退火修复锆石晶格损伤有望从根本上消除α通量差异而成为避免α通量基体效应的可行途径。SOLARI等[25]以2种标准锆石(91500,Plešovice)和5种锆石样品(年龄范围为12～1 000 Ma)为分析对象,对比高温退火处理前后的LA-ICP-MS U-Pb定年结果,结果表明:高温退火处理能够提高LA-ICP-MS锆石U-Pb定年结果的准确度[如退火Plešovice (336.87±0.49) Ma;未退火Plešovice (340.24±0.49) Ma;TIMS (337.13±0.2) Ma],并且显著降低数据的分散度(MSWD降低可达83%,见图9)。

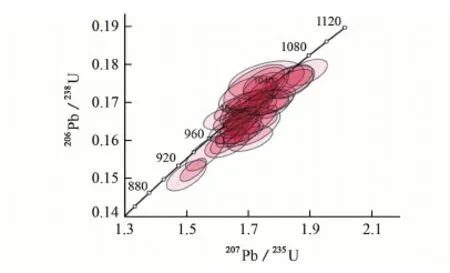
(a) 未退火锆石谐和图

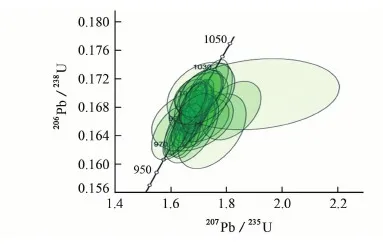
(b) 退火锆石谐和图图9 锆石OC6498退火处理前后的 U-Pb年龄谐和图[25]Fig. 9 Concordia diagrams of LA-ICP-MS U-Pb dating resulits of un-annealed and annealed zircon OC6498[25]

值得思考的是,如何确认退火后锆石的晶体结构是否完全修复,或是如何确认退火后的标准锆石和锆石样品之间不存在α通量(或损伤程度,或结晶程度)的差异？另外,由于不同锆石晶体结构的损伤程度存有很大差异,采用相同的退火条件(如退火温度、时间等)是否能够满足所有锆石修复结构所需？例如SOLARI等[25]研究的锆石Gt0320经高温退火处理后,其LA-ICP-MS U-Pb数据的分散度虽有大幅度下降,仍有相当多的测点数据偏离谐和线。虽然该研究将其解释为可能是普通铅组分的干扰所致,但是基体效应消除的不彻底或者放射铅丢失导致的不谐和都是不能排除的潜在原因。

4 结论

LA-ICP-MS锆石U-Pb定年存在的基体效应是指由于标准锆石和锆石样品基体的差异,使得二者在分析过程中元素和同位素分馏行为不一致,从而导致外标校正技术获得的U-Pb定年结果准确度和精密度降低的一种现象。已有研究表明基体效应的类型主要有元素基体效应、高铀或高Ddpa基体效应和α通量基体效应。

1) 元素基体效应表现为Ca+Al+Fe+Mg或P+U+Th+REE等元素与LA-ICP-MS206Pb/238U年龄差的相关性。然而,元素基体效应尚需更多的研究来确认其是否存在,继而开展该效应的机理研究。

2) 高铀基体效应是由于仪器条件和样品性质共同决定,表现为高铀锆石的铀含量与SIMS206Pb/238U表面年龄的强烈相关性,大都存在着低铀含量的年龄坪区。该效应无法使用单一外标法对高铀锆石的U-Pb数据进行校正。高铀基体效应与锆石自身的辐射损伤程度密切相关,本质上是高Ddpa基体效应。在确定锆石结晶状态的基础上,利用Ddpa>0.08的筛选指标,可以降低该效应对定年结果的影响。

3)α通量基体效应是由于标准样品和未知样品的α通量差异所致,表现为锆石的α通量与LA-ICP-MS206Pb/238U年龄差的强烈相关性。在U-Pb定年分析前,在高温下对标准锆石和锆石样品进行热退火修复,消除二者的α通量差异,可以有效地避免α通量基体效应。

[1] GRAY A L. Analyst[J], 1985,110(5):551-556．

[2] FENG R, MACHADO N, LUDDEN J. Geochim Cosmochim Acta[J], 1993,57(14):3479-3486．

[3] FRYER B J, JACKSON S E, LONGERICH H P. Chemical Geology[J], 1993,211(1/2):47-69．

[4] HIRATA T, NESBITT R W. Geochimical et Cosmochimica Acta[J], 1995,59(12):2491-2500．

[5] YUAN H L, GAO S, DAI M N, et al. Chemical Geology[J], 2008,247(1/2):100-118．

[6] CHANG Z S, VERVOOT J D, MCCELLAND W C, et al. Geochemistry Geophysics Geosystems[J], 2006,7(5):145-162．

[8] GEHRELS G E, VALENCIA V A, RUIZ J. Geochemistry Geophysics Geosystems[J], 2008,9(3):1-13．

[10] SACK P J, BERRY R F, MEFFRE S, et al. Geochemistry Geophysics Geosystems[J], 2011,12(5):99-108．

[11] LI X H, LIU X M, LIU Y S, et al. Science China: Earth Sciences[J], 2015,58(10):1722-1730．

[13] MARILLO-SIALER E, WOODHEAD J, HERGT J, et al. Journal of Analytical Atomic Spectrometry[J], 2014,29(6):981-989．

[14] GUILONG M, HORN I, GÜNTHER D. Journal of Analytical Atomic Spectrometry[J], 2003,18(10):1224-1230．

[15] GÜNTHER D, KOCH J. Formation of aerosols generated by laser ablation and their impact on elemental fractionation in LA-ICP-MS[M]// SYLVESTER P. Laser Ablation ICP-MS in the Earth Sciences: Current Practices and Outstanding Issues. Vancouver: Mineralogical Association of Canada, 2008:19-34．

[16] KROSLAKOVA I, GÜNTHER D. Journal of Analytical Atomic Spectrometry[J], 2007,22(1):51-62．

[17] EGGINS S M, KINSLEY L P J, SHELLEY J M M. Applied Surface Science[J], 1998,127-129:278-286．

[18] HIRATA T. Journal of Analytical Atomic Spectrometry[J], 1997,12(11):1337-1342．

[19] HORN I, VON BLANCKENBURG F. Spectrochim Acta[J], 2007,62(4):410-422．

[20] SYLVESTER P. Matrix effects in laser Ablation ICP-MS[M]//SYLVESTER P. Laser Ablation ICP-MS in the Earth Sciences: Current Practices and Outstanding Issues. Vancourver: Mineralogical Association of Canada, 2008:67-78．

[21] WILLIAMS I S, HERGT J M. U-Pb dating of tasmanian dolerites: a cautionary tale of SHRIMP analysis of high-U zircon[M]//WOODHEAD J D, HERGT J M, NOBLE W P. Beyond 2000: New Frontiers in Isotope Geoscience. Lorne: Abstracts and Proceedings, 2000:185-188．

[22] BLACK L P, KAMO S L, ALLEN C M, et al. Chemical Geology[J], 2004,205(1/2):115-140．

[23] ALLEN C M, CAMPBELL I H. Chemical Geology[J], 2012,332-333:157-165．

[24] GAO Y Y, LI X H, GRIFFIN W L, et al. Lithos[J], 2014,192-195:180-191．

[25] SOLARI L A, ORTEGA-OBREGON C, BERNAL J P. Chemical Geology[J], 2015,414:109-123．

[26] 李冰,杨红霞.电感耦合等离子体质谱原理和应用[M].北京:地质出版社, 2005:104-106．

[27] PETERMAN E M, MATTINSON J M, HACKER B R. Chemical Geolog[J], 2012,312-313:58-73．

[28] BARLING J, WEIS D. Journal of Analytical Atomic Spectrometry[J], 2007,23(7):1017-1025．

[29] BALAN E, NEUVEILLE D R, TROCELLIER P, et al. American Mineralogist[J], 2001,86(9):1025-1033．

[30] MEDRUM A, BOATNER L A, ZINKLE S J, et al. The Canadian Mineralogist[J], 1999,37(1):207-221．

[31] NASDALA L, WENZEL M, VAVRA G, et al. Contributions to Mineralogy and Petrology[J], 2001,141(2):125-144．

[32] NASDALA L, REINERS P W, GARVER J I, et al. American Mineralogist[J], 2004,89(1):219-231．

[33] GARVER J I, KAMP P J. Tectonophysics[J], 2002,349(1/4):203-219．

[34] EWING R C, MELDRUM A, WANG L M, et al. Radiation effects in zircon[M]//HANCHAR J M, HOSKIN P W O. Zircon. Reviews in Mineralogy and Geochemistry. Washington, D.C.: Mineralogical Society of America, 2003:387-425．

[35] RAHN M K, BRANDON M T, BATT G E, et al. American Mineralogist[J], 2004,89(4):473-484．

[36] REINERS P W, CAMPBELL I H, NICOLESCU S, et al. American Journal of Science[J], 2005,305(4):259-311．

[37] BUTERA K M, WILLIAMS I S, BLEVIN P L, et al. Australian Journal of Earth Sciences[J], 2001,48(3):457-464．

[38] LEECH M. Earth and Planetary Science Letters[J], 2008,276(3/4):314-322．

[39] WHITE L T, IRELAND T R. Chemical Geology[J], 2012,306-307(19):78-91．

[40] PALENIK C S, NASDALA L, EWING R C. American Mineralogist[J], 2003,88(5/6):770-781．

[41] NASDALA L, LENGAUER C L, HANCHAR J M, et al. Chemical Geology[J], 2002,191(1):121-140．

[42] YAMADA R, TAGAMI T, NISHIMURA S, et al. Chemical Geology[J], 1995,122(1/4):249-258．

[43] HORN I, RUDNICK R L, MCDONOUGH W F. Chemical Geology[J], 2000,167(3/4):405-425．

[44] TIEPOLO M, BOTTAZZI P, PALENZONA M, et al. Canadian Mineralogist[J], 2003,41(2):259-272．

[45] ZHAO K D, JIANG S Y, LING H F, et al. Chemical Geology[J], 2014,389:110-121．

[46] WANG X L, COBLE M A, VALLEY J W, et al. Chemical Geology[J], 2014,389:122-136．