基于秘密共享的(t,m,n)-AS组认证方案
,,
(中国科学技术大学 计算机科学与技术学院,合肥 230027)
0 概述
身份认证是保障通信安全的重要手段,在日益复杂的网络通信环境中,高效的身份认证机制成为信息安全专家研究的重点之一。传统身份认证有2种基本的实现方式:无第三方参与的认证和有第三方参与的认证。在无第三方参与的认证系统中,认证双方利用事先共享的秘钥或者公开秘钥体制进行身份认证;在有第三方参与的认证系统中,认证双方在可信认证中心的支持下验证彼此的身份。
现有的认证方案大多都是一对一的认证[1-4],即认证方每次认证一个用户。但是很多网络应用,如网络会议、电子拍卖等,往往采用面向组的认证模式,即要求认证方案一次完成对组内所有成员的认证,这类认证被称为组认证。目前已经存在很多种组认证方案,例如:文献[5]针对Ad Hoc网络提出的基于可信第三方的组认证方案,利用一种公钥基础设施PKI认证各个网络节点;文献[6]改进著名协议Kerberos提出的组认证方案Kaman,可以更好地适用于Ad Hoc网络;文献[7]针对Ad Hoc提出的EAP协议,将整个Ad Hoc网络作为一个群组,并利用认证服务器(Authorization Server,AS)作为群组和其他网络认证的媒介,所有组内成员的身份认证都由AS完成;文献[8]提出的另一种组认证方案mGAP,通过管理域名预测移动节点行为并管理节点和组之间的认证;Harn提出的分布式组认证方案(t,m,n)-GAS,可以在O(1)时间内认证所有的参与者。该方案在注册阶段利用Shamir(t,n)秘密共享机制[10]为注册的成员发送k个share。在认证阶段,参与认证的m个参与者每人利用自己的share生成一个令牌,并收集其他参与者的令牌恢复秘密s,从而确认m个参与者是否属于预先定义的一个组;文献[11]提出的开放式PKI认证模型,改进了传统的PKI方案,利用CA独立完成2个验证服务,从而提高了CA的信任度;文献[12]提出的一对多认证的基本框架,不仅可以用于成员之间的互相认证,还可用于服务器和客户端之间的认证。作为一种通用框架,该方案允许使用不同的公钥机制(如Diffie-Hellman、DLP等)进行实现;在文献[13]针对Ad Hoc网络提出的基于线性配对无AS的组认证方案中,任何用户都可以快速生成一个组,组成员的人数不受限制,且组成员之间可以互相认证并生成会话密钥;文献[14]则提出了一种基于Shamir秘密共享机制且支持欺骗检测的组认证方案。
现有的组认证方案[5-6,8]多为拥有AS的集中式认证方案,但都是基于公钥密码机制实现,因而计算复杂,效率低下。这些方案都是一对一的认证方案,不能一次认证所有参与者。方案[15-16]是无AS的认证方案。方案[9]是基于秘密共享的分布式方案,虽然可以快速完成对所有组成员的认证,但是需要多个多项式且不够灵活,并且该方案只能判断组内是否存在非法成员,但是存在非法成员的情况下,无法确定具体的非法成员。
考虑以下应用场景:一组人计划在某个时间举行一个网络会议,在会议开始之前所有参会人员可以随时向认证服务器提交自己的身份信息,但是为提高认证效率,希望认证服务器在收到所有参会人员的身份信息之后,通过一次计算就能够认证所有参与者,并且在有非法参与者的情况下对其进行隔离,保障会议顺利进行。上述组认证的方案难以满足该应用场景的要求。
本文基于Shamir秘密共享机制,提出一种包含组认证服务器的(t,m,n)组认证方案,并对其正确性和安全性加以验证。
1 基础知识
1.1 Shamir(t,n)秘密共享机制
(t,n)秘密共享[10]的基本设计思想是将一个秘密分割成n份share,并将每个share分发给一个参与者,只有t(t≤n)个或t个以上的参与者合作才能恢复秘密,少于t个参与者无法恢复秘密。方案包含一个Dealer及n个share持有者U={U1,U2,…,Un},t为门限,该方案包括2个算法:
1)share生成算法
Dealer随机选择一个大素数p,并在有限域GF(p)上选一个(t-1)次的随机多项式f(x)=a0+a1x+…+at-1xt-1(modp),令秘密s=f(0)=a0∈GF(p),ai,i=1,2,…,t-1∈GF(p)。Dealer计算n个share,si=f(xi),i=1,2,…,n,xi是与Ui有关的公开信息。然后,Dealer通过安全信道将si秘密地发送给share持有者Ui。
2)秘密恢复算法
如果m(t≤m≤n)个share持有者(即参与者),如{U1,U2,…,Um}需要联合恢复秘密s,则m个share持有者互相交换share,通过以下公式恢复秘密s:
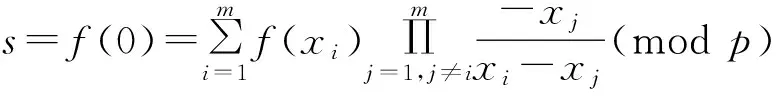
在该方案中,任意大于等于t个参与者合作可以恢复秘密,而少于t个参与者得不到关于秘密的任何信息,因此,可以抵御t个以下参与者的联合攻击。该方案不基于任何的数学假设,是无条件安全的。
1.2 Harn(t,m,n)组认证方案
文献[9]提出了一种分布式的(t,m,n)组认证方案,可以在O(1)时间内认证所有参与认证的用户是否属于预先定义的组。该方法具体描述如下:
1)注册阶段
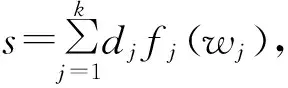
2)认证阶段
如果有m(t≤m≤n)个用户,若{Ui|i=1,2,…,m}需要互相认证,则每个用户利用自己的k个share生成一个令牌ti:
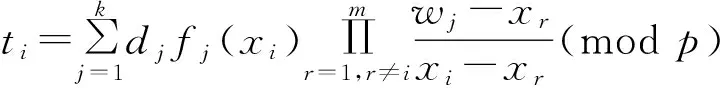
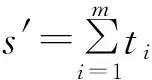
该方案基于秘密共享,在不依赖任何数学假设的前提下完成了对m个参与者的快速认证。但是该方案要求kt>(n-1),因而限制了门限t和参与者n的选择,不够灵活,并且该方案只能判断所有参与认证的用户是否属于预先定义的组,在有非法参与者的情况下没有给出有效的解决方案。
2 本文(t,m,n)-AS组认证方案
本文基于Shamir秘密共享提出一种(t,m,n)-AS组认证方案,其中:t为门限;m为参与认证的参与者个数;n为组内成员个数;AS为认证服务器。该方案共分为3个阶段,分别为注册阶段、整体认证阶段和单一认证阶段。在整体认证阶段,AS认证所有参与者中是否存在非法参与者,如果存在非法参与者,AS可以在单一认证阶段确定所有的非法参与者。在单一认证阶段,AS无需与参与者进行进一步交互。
2.1 实体
本文方案的包括1个组管理员GM、1个组认证服务器AS和若干参与者,具体如下:
1)组管理员GM:假设GM对于所有参与认证的成员是可信的。GM负责多项式参数及秘密的选择、计算并公开秘密的Hash值、生成shares并安全地分发给组成员。组管理员只参与方案的注册阶段。
2)组认证服务器AS:假设AS对所有组成员是可信的,并且在AS和任意组成员之间有私有信道。AS负责方案的整体认证和单一认证。
3)参与者:称在组管理员处成功注册获得有效share的用户为组成员。在认证阶段所有参与认证的用户为参与者。
本文假设在认证阶段所有参与者事先知道参与者数量及所有参与者的公开身份信息,例如参与网络会议的人员可以事先通过会议通知中的参会人员列表等途径了解要参与会议的人员。
2.2 攻击模型
本文考虑2种攻击模型,即非成员攻击者和成员攻击者。
1)非成员攻击者:非成员攻击者不是合法的组成员,和组管理员以及AS之间没有私有信道。他们自身没有share,但是可能通过破解组成员和AS之间的信道获得令牌。本文假设非成员攻击者最多可以获取(m-1)个参与者的令牌。
2)成员攻击者:成员攻击者是合法的组成员且有有效share,但是他们可能串谋破坏认证或者企图帮助非法参与者通过认证。本文假设最多有(t-1)个成员攻击者合谋攻击。
2.3 具体方案
本文方案包括注册阶段和认证阶段。
1)注册阶段

同时,GM为组认证服务器AS生成2×(t-1)个share:f1(xk),f2(xk)(k=n+1,n+2,…,n+t-1),并安全地发送给AS。然后,GM在GF(p)上选择2个数对(a1,b1)、(a2,b2),组成2个秘密:s1=a1f1(0)+b1f2(1)(modq)和s2=a2f1(0)+b2f2(1)(modq),使得s1、s2均在GF(q)上。GM计算s1和s2的单向哈希值H(s1)、H(s2),公开(a1,b1)、(a2,b2)及单向哈希函数H(·)。share分发过程如图1所示。
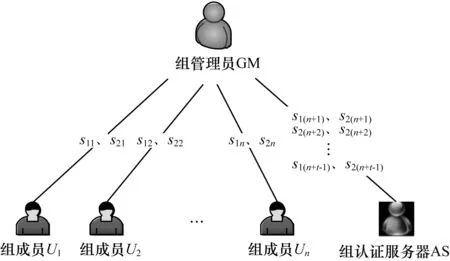
图1 share分发过程
2)认证阶段
认证阶段分为2个步骤,分别为统一认证和单一认证。统一认证是指AS确定所有参与者中是否存在非法参与者,而单一认证是指AS在不与参与者进一步交互的情况下确定所有的非法参与者。AS首先对所有参与者进行统一认证。
(1)统一认证
假设任意m(t≤m≤n)个用户参与认证,其身份的下标集合记为Im⊆{1,2,…,n},|Im|=m,每个参与者Ui(i∈Im)计算2个令牌t1i,t2i(其中r1i、r2i是用户Ui在GF(q)上选择的随机数)。Ui将t1i、t2i通过私有信道发送给AS。AS利用自己的share计算令牌tas(其中r是在GF(q)上选择的随机数)。
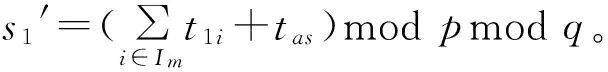
(2)单一认证
存在非法参与者时,AS可以直接对所有参与者进行单一认证,具体认证过程为:AS在对参与者Ui进行认证时,利用自己的share生成令牌ti(其中,ri为AS在GF(q)上均匀选择的某个随机数)。然后,AS计算s2′=(t2i+ti)modpmodq以及H(s2′);如果H(s2′)=H(s2),则Ui为组成员,否则Ui为非法参与者。对所有参与者进行此计算,可以在O(n)时间确定所有非法参与者。
3 方案正确性及安全性分析
3.1 方案的正确性分析
对本文方案进行正确性分析,具体如下:
1)统一认证过程的正确性分析
假设AS收集的所有参与者的令牌都合法有效,则一定能够通过统一认证,因为:

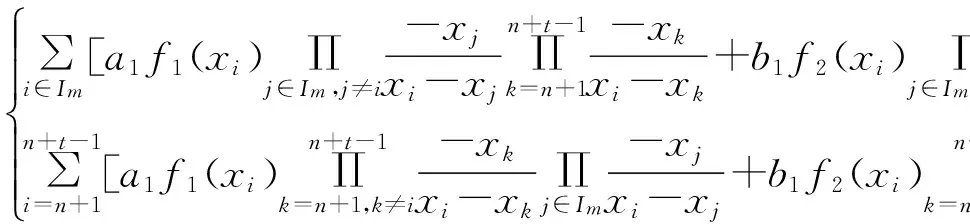
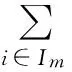

2)单一认证的正确性分析
在对某个特定参与者进行单一认证时,假设参与者提供合法的令牌,则可以通过单一认证,计算公式如下:
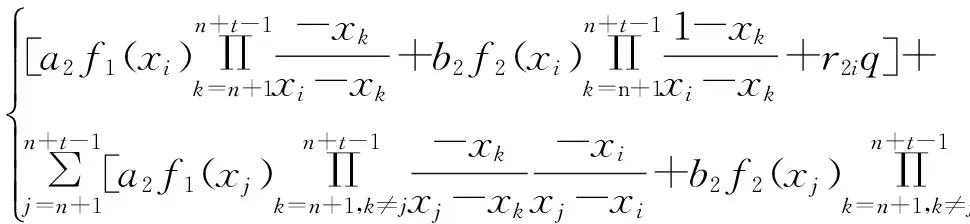
[s2+(r2iq+riq)]modpmodq=s2
因为s2+r2iq+riq 本文在认证阶段考虑成员和非成员2种攻击者。非成员攻击者没有合法shares无法生成有效的令牌,但是它们可能破解AS与参与者之间私密信道从而获得参与者的令牌。成员攻击者有合法share,但是它们可能在少于t个成员情况下串谋企图通过认证或者帮助非成员伪造share。 定理1给定某个参与者的令牌,攻击者无法得到参与者的share,即通过令牌获得其share的最大概率为1/q。 证明:假设用户Ui的share为s1i、s2i,其公开身份信息为xi。在认证阶段利用Ui的s1i、s2i生成令牌t1i、t2i,并发送给AS。攻击者破解AS和Ui之间的安全信道获得t1i、t2i: 将t1i、t2i用以下公式表示: t1i=(α1s1i+β1s2i+r1iq)modp t2i=(α2s1i+β2s2i+r2iq)modp 其中,α1、β1、α2、β2、p、q是已知信息,r1i、r2i都是GF(q)上的未知随机数,化简得: s1i=(β2α1-β1α2)-1[β2t1i-β1t2i+(β1r2i-β2r1i)q]modp 因为r1i、r2i是未知的,对于任意的r1i、r2i都会有对应的s1i,由大数定律可知,当β1=-β2且r1i、r2i分别在[0,q-1]均匀变化时,β1r2i-β2r1i最多有q个相同的值,因此通过t1i,t2i获得s1i的最大概率为q/q2=1/q,与直接在GF(q)上猜测s1i的概率相同。同理获得s2i的最大概率也为1/q。 定理2(t-1)个成员攻击者串谋无法通过整体认证,即(t-1)个成员攻击者破解秘密s1的概率为1/q。 假设有(t-1)个成员,如U={U1,U2,…,Ut-1},其中 Ui∈U的share为s1i、s2i,t-1个组成员试图串谋恢复秘密s1=a1f1(0)+b1f2(1)(modq)。欲恢复s1,需要确定f1(0)、f2(1)。先考虑f1(0),(t-1)个组成员利用他们的s1i,i=1,2,…,t-1得到以下方程组: 写成矩阵形式XC=S,即: X的秩最大为(t-1) 定理3非成员攻击者即使截取(m-1)个参与者的令牌,也无法通过整体认证。确切地讲,用(m-1)个参与者的令牌破解s1的概率为1/q。 证明:非成员攻击者想要通过整体认证有2种可能的途径。一种是攻击者得到(m-1)个参与者的令牌后,尝试从令牌恢复share,当(m-1)≥t时,攻击者可以通过(m-1)个share直接恢复多项式,从而计算出秘密s1;另一种是尝试直接通过令牌恢复秘密s1。下面分别证明2种方案破解s1的概率都为1/q。 1)假设非成员攻击者截获了U={U1,U2,…Um-1},这(m-1)个参与者与AS之间的私有信道并成功获取他们的令牌t1i,t2i,i∈Im。由定理1可知通过令牌获取share的最大概率为1/q,与直接猜测s1的概率相同,因此,无法通过令牌恢复多项式并通过认证。 2)假设非成员攻击者能够利用(m-1)个参与者的令牌直接恢复秘密出s1,则有: 由上式得: t1mmodpmodq=0 ⟹t1mmodp=αq 其中,α为整数,当f1(x)、f2(x)的系数ci、di在GF(P)上呈均匀分布时,t1m在GF(P)上也是均匀分布的[17],则t1mmodp=αq成立的概率为(⎣p/q」+1)/p,当q趋于无穷大时,此概率趋近于1/q,即(m-1)个参与者通过整体认证的概率约为1/q。 综上所述,定理3得证。 定理4参与者无合法令牌无法通过整体认证和单一认证,即如果参与者无合法令牌时,AS成功恢复秘密s1、s2的概率均约为1/p。 证明: 1)假如有m个参与者参与整体认证而其中一个参与者无合法令牌,想要通过整体认证,即等价于(m-1)个参与者通过认证,由定理3可知,(m-1)个参与者恢复秘密s1的概率约为1/p。} 2)假设对参与者Ui进行单一认证,AS针对Ui生成令牌ti若在Ui无合法令牌的情况下,AS恰好成功恢复秘密s2,则有s2=(ti+t2i′) modpmodq=(ti+t2i)modpmodq,推得(t2i-t2i′)modpmodq=0,即(t2i-t2i′)modp=αq。其中,α为整数,t2i′为Ui任意伪造的非法令牌。与定理3类似,对于某一伪造令牌t2i′,当q趋于无穷大时,(t2i-t2i′)modp=αq成立的概率趋近于1/q。因此参与者在无合法令牌时通过单一认证的概率约为1/q。 综上所述,定理4得证。 从3个方面分析本文方案的特性: 1)实用性。与Harn方案类似,本文方案不要求所有参与者同时将令牌发送给AS,在认证之前的任何时刻都可以随时发送令牌。然而,Harn的方案要求kt>(n-1),多项式的个数(即每个人持有的share个数)和门限制约着参与者的人数。在门限不变的情况下,随着n的增大,所需的多项式个数会越来越多,每个成员需要持有的share也越来越多。而本文方案在任何情况下都只需要2个多项式,每个参与者持有2个share。同时,文献[9]的方案无法确定具体的非法参与者,而本文方案在整体认证的基础上还可以对参与者进行单一认证,从而可以快速地确定非法参与者。因此,从存储代价、通信代价,以及方案的完整性方面,本文方案具有更高的实用价值。 2)高效性。相对于一对一的认证方案[1-2],本文方案实现了一对多认证,AS可以在O(1)时间内确定所有的参与者是否都是组成员。相对文献[5,8]方案,该方案不依赖公钥密码系统,计算简单。相对于文献[9]方案中每个参与者只需要两个令牌,降低了存储复杂度。而且在任何用户和服务器之间只需要一次通信。 3)健壮性。该方案基于(t,n)门限秘密共享,可以抵御(t-1)个成员攻击者的联合攻击。因为方案不是直接使用share而是通过构造令牌的方式参与认证,使得非成员攻击者在截取了(m-1)个参与者令牌的情况下仍然无法通过认证。该方案不基于任何的计算假设,因而是理论上安全的。 本文针对网络会议、Ad Hoc网络、电子拍卖等面向组的应用,提出了一种集中式的(t,m,n)-AS组认证方案。在注册阶段,GM为每个组成员分发2个share;在认证阶段,参与者利用share构造2个令牌发送给AS用于整体认证和单一认证。该方案不仅可以抵御(t-1)个成员攻击者联合伪造令牌攻击,而且可以阻止非成员攻击者在截取多达(m-1)个参与者令牌的情况下通过认证。本文方案不依赖于任何数学难题,在理论上是安全的。但其未考虑组成员动态变化的情况,而且在认证之前,参与者必须事先知道哪些参与者参与认证,这也使得使用场景受限。因此,下一步将研究动态群组的组认证问题,并突破必须预知参与者身份这一限制。 [1] DAS M L.Two-factor User Authentication in Wireless Sensor Networks[J].IEEE Transactions on Wireless Communications,2009,8(3):1086-1090. [2] OPPLIGER R,HAUSER R,BASIN D.SSL/TLS Session-aware User Authentication[J].Computer,2008,41(3):59-65. [3] 王 帅,常朝稳,魏彦芬.基于云计算的USB Key身份认证方案[J].计算机应用研究,2014,31(7):2130-2134. [4] 谢 璇,王瑞刚,杨小宝,等.一种SD卡用户身份认证方案的设计与实现[J].电子科技,2015,28(6):57-60. [5] PIRZADA A A,MCDONALD C.A Review of Secure Routing Protocols for Ad Hoc Mobile Wireless Networks[C]//Proceedings of the 2nd Workshop on the Internet,Telecommunications and Signal Processing.Berlin,Germany:Springer,2003:57-80. [6] PIRZADA A,MCDONALD C.Kerberos Assisted Authentication in Mobile Ad-Hoc Networks[C]//Proceedings of the 27th Australasian Computer Science Conference.Dunedin,New Zealand:[s.n.],2004:41-46. [7] BHAKTI M A C,ABDULLAH A,JUNG L T.EAP-based Authentication for Ad Hoc Network[C]//Proceedings of Seminar Nasional Aplikasi Teknologi Informasi Conference.Yogyakarta,Indonesia:[s.n.],2007:133-137. [8] ABOUDAGGA N,QUISQUATER J J,ELTOWEISSY M.Group Authentication Protocol for Mobile Networks[C]//Proceedings of the 3rd IEEE International Conference on Wireless and Mobile Computing,Networking and Communications.Washington D.C.,USA:IEEE Press,2007:28. [9] HARN L.Group Authentication[J].IEEE Transactions on Computers,2013,62(9):1893-1989. [10] SHAMIR A.How to Share a Secret[J].Communications of the ACM,1979,22(11):612-613. [11] 周晓斌,许 勇,张 凌.一种开放式PKI身份认证模型的研究[J].国防科技大学学报,2013,35(1):169-174. [12] YANG H,JIAO L,OLESHCHUK V A.A General Framework for Group Authentication and Key Exchange Protocols[M].Berlin,Germany:Springer,2014. [13] FENG W,CHANG C C,CHOU Y C.Group Authentication and Group Key Distribution for Ad Hoc Networks[J].International Journal of Network Security,2015,17(2):199-207. [14] GUO C,ZHUANG R,YUAN L,et al.A Group Authentication Scheme Supporting Cheating Detection and Identification[C]//Proceedings of the 9th International Conference on Frontier of Computer Science and Technology.Washington D.C.,USA:IEEE Press,2015:110-114. [15] CABALLERO-GIL P,HERNNDEZ-GOYA C.Self-organized Authentication in Mobile Ad-Hoc Networks[J].Journal of Communications and Networks,2009,11(5):509-517. [16] CAPKUN S,BUTTYAN L,HUBAUX J P.Self-organized Public-key Management for Mobile Ad Hoc Networks[J].IEEE Transactions on Mobile Computing,2003,2(1):52-64. [17] MIAO F Y,XIONG Y,WANG X F.Randomized Component and Its Application to (t,m,n)-group Oriented Secret Sharing[J].IEEE Transactions on Information Forensics and Security,2015,10(5):889-899.3.2 安全性分析

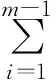
4 方案特性
5 结束语

