单级齿轮箱内部冲击振动的传播衰减特性研究

张建宇，陈 林，胥永刚

（1.北京工业大学 先进制造技术北京市重点实验室，北京 100124；

2.北京工业大学 北京市精密测控技术与仪器工程技术研究中心，北京 100124）

1 引言

齿轮箱是机械设备中用以连接和传递动力的通用零部件，是许多机械装置中的重要组成机构，其动态特性对整个设备的运行至关重要。齿轮箱振动信号中包含了大量的设备状态信息，在齿轮箱表面设置传感器获得箱体表面的振动信号，并对该信号进行分析处理获得齿轮箱内部的激励情况，是判断齿轮箱劣化程度和运行状态的主要方法。而振动信号的采集质量，取决于内部激励源到箱体拾振点之间的传播特性，因此，研究冲击振动历经各个界面的衰减特性至关重要。

近年来，针对齿轮箱系统的冲击激励和动态响应特性，国内外学者进行了广泛深入的研究。文献[1]对斜齿轮系和行星轮系的动力特性进行了分析，并通过动态试验分析了齿轮受迫时的响应特征。文献[2]将数值计算和试验相结合，获得了一款汽车变速齿轮箱的齿轮冲击激励。文献[3]通过研究得到船舶在冲击激励作用下的振动响应结果。文献[4]通过冲击试验，获得冲击振动在通过“齿轮-轴-轴承-轴承座-金属板”多界面时的能量损耗关系。文献[5]建立了齿轮箱完整的有限元模型，得到模型在内部激励作用下的振动响应。文献[6]建立了风电齿轮箱耦合非线性有限元模型，采用Lanczos法获得了齿轮箱系统的固有特性。文献[7]将集中参数法和有限元法相结合，建立了风电齿轮箱的动力学模型，计算得到箱体在动态啮合力作用下的振动响应。文献[8]通过分析行星齿轮箱内部每个啮合冲击的传递路径，建立了行星齿轮箱的振动信号仿真模型，得到了齿轮故障时的振动响应。文献[9]建立了齿轮箱的有限元模型，分析得到人字齿轮传动系统的振动传递特性。文献[10]建立齿轮箱动力学模型，从传递函数的角度分析了振动信号在齿轮箱传递路径中的变化情况。

建立了QPZZ-II故障模拟实验台中单级齿轮箱的有限元模型，通过模态叠加法计算得到齿轮箱在内部脉冲激励下各节点的振动响应。对振动响应信号进行时域分析获得振动幅值能量、能量传递损耗率等参数，从而定量分析了齿轮箱内部冲击振动的传播衰减特性。同时采用脉冲响应试验获得齿轮箱各级拾振点的动态响应情况，通过时域对比分析，验证了有限元模型计算结果的准确性。

2 齿轮箱内部振动传播的数值仿真

2.1 结构的动力学建模

QPZZ-II故障模拟实验台中的齿轮箱为单级齿轮箱，该齿轮箱由一对齿轮副、主动轴、从动轴、箱体和4个型号为6206Z的轴承组成，如图1所示。其中齿轮副参数，如表1所示。借助ABAQUS建立齿轮箱有限元模型，如图2所示。齿轮箱泊松比为0.3，弹性模量为210，齿轮箱与地面采用螺栓连接，因此该模型边界条件设定螺栓连接处为固定约束。轮齿啮合区采用面与面接触约束，齿轮与轴采用绑定约束。每个轴承简化为呈“十”字形分布的四个弹簧单元。采用六面体C3D8R单元对齿轮箱进行网格划分，共划分206045个节点，166122个单元。

图1 齿轮箱实物图Fig.1 Figure of Gearbox

图2 齿轮箱系统的有限元模型Fig.2 The FEM Model of Gearbox

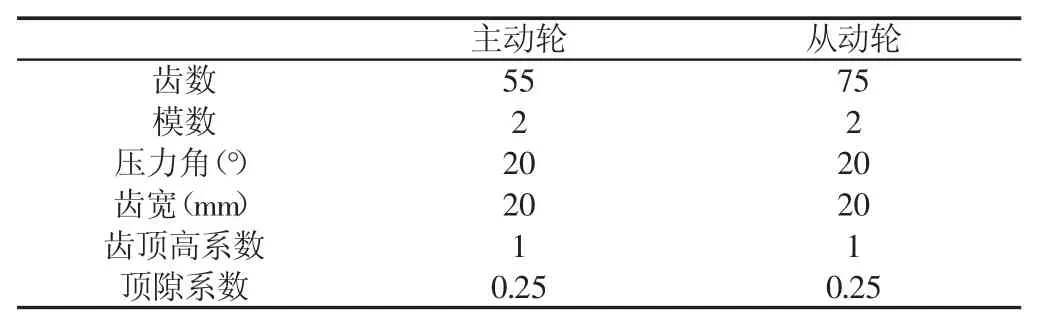
表1 齿轮副基本参数表Tab.1 Basic Parameters of Gear

2.2 齿轮箱的冲击响应分析

2.2.1 模态叠加法

模态叠加法是求解线性系统动态响应的简便方法，基本思路是通过坐标变换，将一个多自由度系统的N个耦合运动方程分解为N个非耦合的运动方程。对解耦后的各个独立的二阶线性微分方程进行求解，并将各微分方程的计算结果进行线性组合便得到系统的动态响应。一般的多自由系统动力学问题的基本方程为：

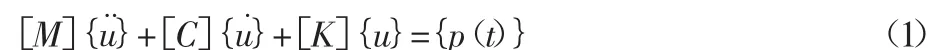
式中：［K］—系统的总刚度矩阵；［C］—系统的阻尼矩阵；［M］—系

统的质量矩阵；｛u｝—系统的位移向量。其特征方程为：

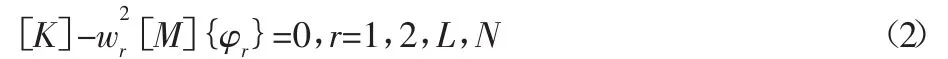
其中，特征值所对应的特征向量｛φr｝是正交的，同时｛φr｝对刚度矩阵［K］及质量矩阵［M］也是正交的，即：

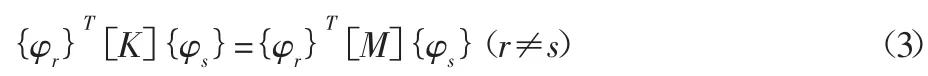
为将物理坐标表示的动力学方程（1）解耦，需将其转换到模态坐标系，根据特征向量的正交性，获得模态坐标系下方程的模态矩阵［φ］、模态质量［Mr］、模态刚度［Kr］、模态阻尼［Cr］，具体定义如下：

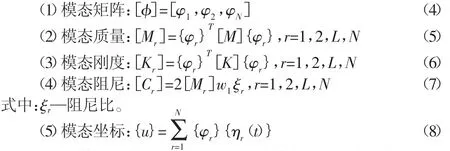
其中，模态坐标｛ηr（t）｝—与第r阶模态相应的主坐标。

通过以上变换，将耦合的动力学方程解耦成以模态坐标表示的模态方程：［Mr］｛η¨｝+［Cr］｛η˙｝+［Kr］｛η｝=｛p（t）｝，r=1，2…N（9）

通过求解式（9）式表示的N个独立的模态坐标下的动力学方程，就可得到模态坐标下的各阶向量，将其代入式（8）可得系统在物理坐标系下的位移响应｛u｝，进而可求得系统的加速度响应。

2.2.2 齿轮箱动态响应仿真结果

采用模态叠加法分析齿轮箱的动态响应，首先分析其固有模态。采用Lanczos法对图2所示的齿轮箱进行有限元模态分析，获得齿轮箱系统前七阶模态的固有频率和振型，如表2所示。

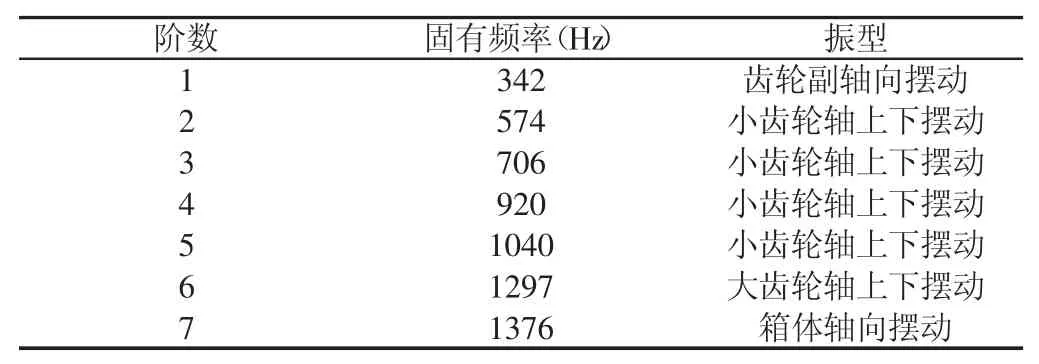
表2 齿轮箱系统的前七阶模态参数Tab.2 First Seven Order Modal Parameters of Gearbox

在大齿轮轮齿处施加一个垂直齿面的激励力来模拟齿轮箱内部冲击，该激励力的时域波形，如图3所示。激励点的位置如图4中P点所示。采用模态叠加法求解动力学响应，得到齿轮箱系统上任意点的振动位移、速度和加速度数值。

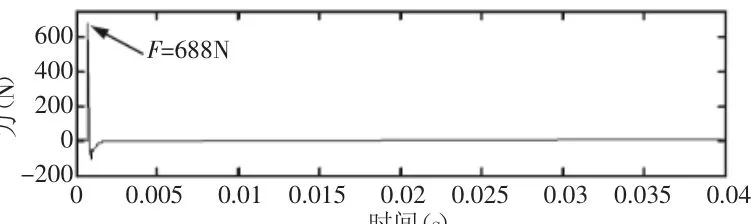
图3 激励点处的时域信号Fig.3 The Time Domain Signal of Incentive Point

图4 齿轮箱有限元模型中激励点和响应点的位置Fig.4 Excitation and Response Points Location in FEM Model of Gearbox

齿轮箱内部的冲击振动以波的形式向外传播，因此可能存在多种传播路径。选择两条路径加以讨论，路径一：P-1-2-3，其中P为激励点，1位于大齿轮激励点附近，2位于大齿轮轴上，3位于齿轮箱结合面上；路径二：P-1-4-5-6，其中4位于大齿轮轮齿啮合区附近，5位于小齿轮轮齿啮合区附近，6位于小齿轮轴上。分别提取拾振点1，2，3，4，5，6处的振动时域响应信号，各响应点的加速度时域信号，如图5～图10所示。

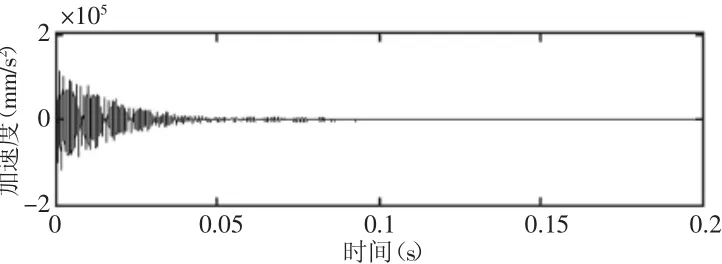
图5 响应点1处的加速度时域波形图Fig.5 Time Domain Signal of Acceleration at Response Point 1

图6 响应点2处的加速度时域波形图Fig.6 Time Domain Signal of Acceleration at Response Point 2

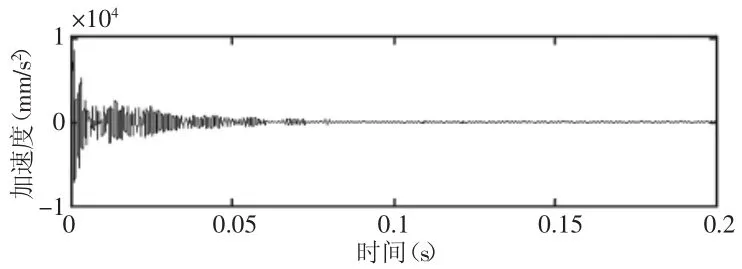
图7 响应点3处的加速度时域波形图Fig.7 Time Domain Signal of Acceleration at Response Point

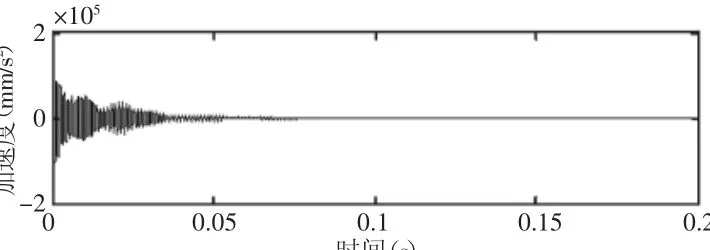
图8 响应点4处的加速度时域波形图Fig.8 Time Domain Signal of Acceleration at Response Point 4

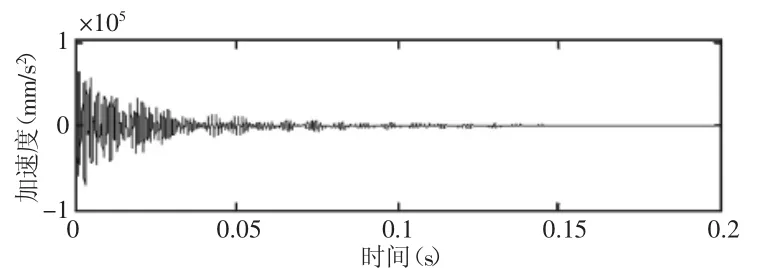
图9 响应点5处的加速度时域波形图Fig.9 Time Domain Signal of Acceleration at Response Point 5

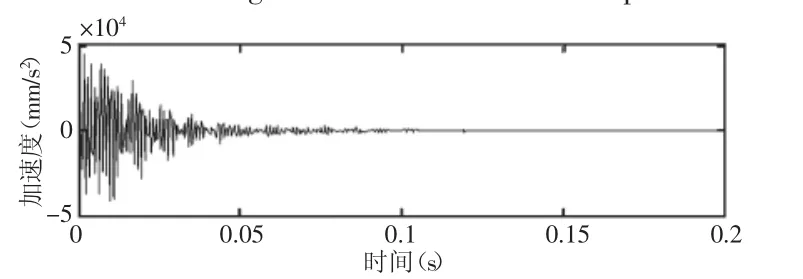
图10 响应点6处的加速度时域波形图Fig.10 Time Domain Signal of Acceleration at Response Point 6

2.3 冲击振动衰减特性的定量分析

2.3.1 能量传递损耗率

冲击振动在结构内的传播过程本质上是由能量集中的脉冲信号转变成能量分散且随时间衰减的振荡信号的过程，其损耗关系难以准确地在时域图上描述，因此引入能量传递损耗率的概念。首先用振动信号的均方值表示振动幅值能量，进而定义冲击振动能量通过某界面的传递损耗率ηi为：

式中：AE0i—界面上的输入振动幅值能量；AE1i—界面上的输出振动幅值能量。

2.3.2 内部冲击振动的传递损耗率分析

齿轮箱内部冲击激励产生的振动信号通过多条路径传递到箱体。由于响应点1与激励点P位置接近，激励点P处的振动能量即由响应点1的能量表示。对传递路径一“P-1-2-3”和传递路径二“P-1-4-5-6”中各响应点的加速度信号进行统计分析，获得各响应点的振动幅值能量，进而得到冲击振动在两条传播路径中的能量传递损耗率。各响应点的振动幅值能量，如表3所示。表4和表5分别为路径一和路径二中各响应点间的能量传递损耗率。

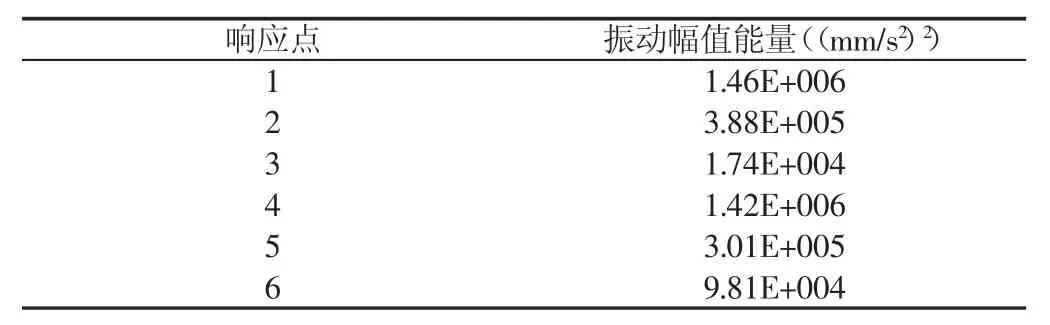
表3 各响应点的振动幅值能量Tab.3 Vibration Amplitude Energy at Response Points

表4 传递路径一中冲击振动能量在各个响应点间的传递损耗率Tab.4 Energy Transfer Loss Rate Between Response Points in Path 1

如表4所示，传递路径一“P-1-2-3”中，内部冲击振动能量大部分损耗在大齿轮（响应点1）到大齿轮轴（响应点2）界面间，能量传递损耗率为73.4%；大齿轮（响应点1）到箱体（响应点3）界面间的能量传递损耗率为98.8%，传递到箱体上的能量仅为总能量的1.2%；相邻界面间能量传递损耗率的最大值为95.5%，发生在大齿轮轴（响应点2）到箱体（响应点3）界面间。

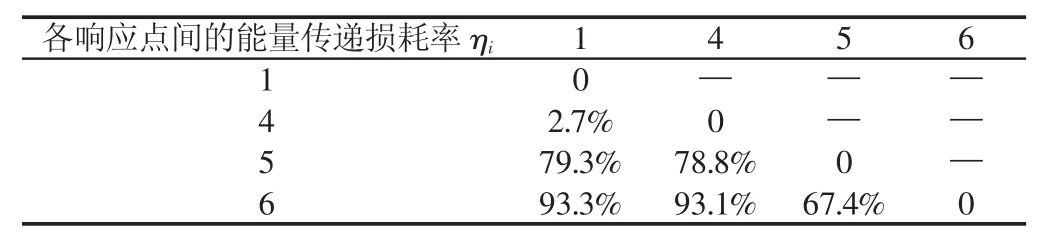
表5 传递路径二中冲击振动能量在各个响应点间的传递损耗率Tab.5 Energy Transfer Loss Rate Between Response Points in Path 2

如表5所示，传递路径二“P-1-4-5-6”中，大齿轮上响应点1和响应点4间的能量传递损耗率仅为2.7%。内部冲击振动能量大部分损耗在大齿轮与小齿轮啮合区处，大齿轮响应点1和响应点4到小齿轮（响应点5）间能量传递损耗率分别为79.3%和78.8%。小齿轮（响应点5）到小齿轮轴（响应点6）间的能量传递损耗率为67.4%。

3 齿轮箱振动传播特性的实验研究

3.1 冲击振动测试方案

齿轮箱实物图及振动测点的布置方案，与仿真模型相对应，如图11所示。激励点选择在大齿轮轮齿处，试验设备包括：INV MSC-3中型冲击锤，数据采集及分析仪器DASP以及INV 9822A型加速度传感器。设置脉冲冲击试验采样频率为25600Hz，采样点数为10240。参照仿真模型中的传递路径设计，选择几个关键点进行实验验证。激励点P与三个响应测点1，2，3的位置与有限元模型中的各点相对应。激励载荷与数值仿真中激励力大小相同。冲击锤在激励点处敲击，该激励产生的振动信号通过设置在传递路径上的三个响应测点1，2，3进行测量。

图11 齿轮箱试验台激励点及响应点位置。Fig.11 Excitation and Response Points Location in Gearbox Test Bench

3.2 冲击振动测试结果

脉冲冲击试验得到的响应点1，2，3的加速度时域波形图，如图12～图14所示。

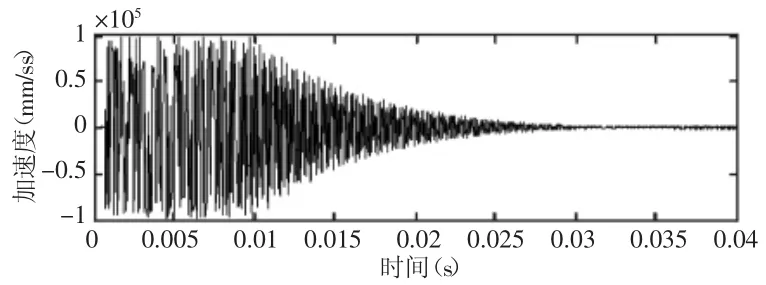
图12 实测的响应点1处加速度响应Fig.12 Measured Acceleration Response at Response Point 1

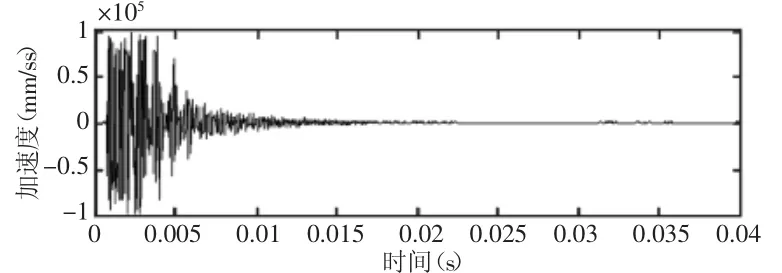
图13 响应点2处的加速度时域波形Fig.13 Measured Acceleration Response at Response Point 2

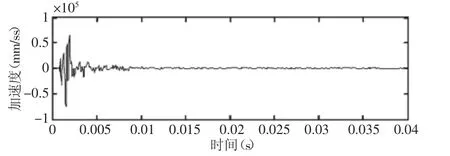
图14 响应点3处的加速度时域波形Fig.14 Measured Acceleration Response at Response Point 3

3.3 测试与仿真结果的对比分析

通过对试验中各测点的加速度信号进行统计分析，获得各响应点的振动幅值能量，并将其与仿真结果作对比，如表6所示。表中三个响应点1，2，3处的振动幅值能量的仿真和试验结果误差均低于5%，从而可以验证仿真结果的准确性。

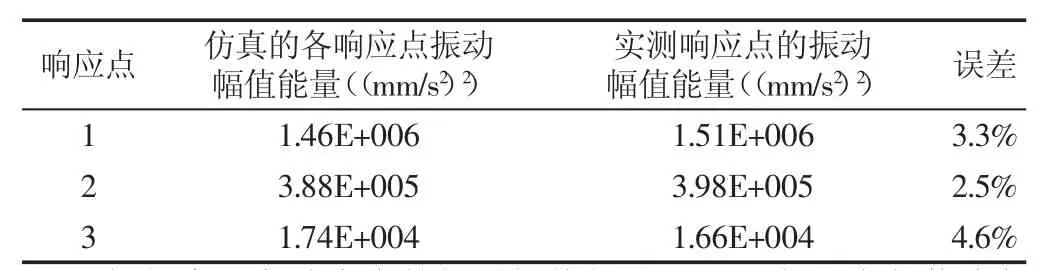
表6 振动幅值能量的仿真和试验结果对比Tab.6 Vibration Amplitude Energy Contrast in Simulation and Test

各点传递过程中的能量传递衰减率，该试验分析结果与有限元仿真对比，如表7所示。通过表7可知，响应点1，2，3间的能量传递损耗率的仿真结果和试验结果误差均在5%以内，从而证明数值仿真的准确性。

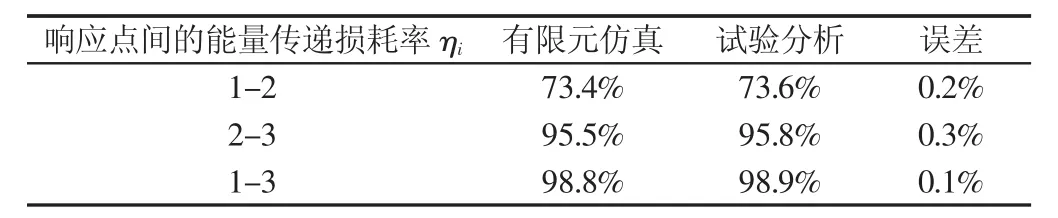
表7 各响应测点的能量传递损耗率（试验结果）Tab.7 Energy Transfer Loss Rate Between Response Points

4 结论

以QPZZ-II故障模拟平台中的齿轮箱为研究对象，采用有限元仿真和冲击测试手段研究了齿轮箱内部冲击振动能量沿不同传播路径的传播与衰减情况，并通过振动幅值能量和能量传递损耗率两个参数实现了衰减特性的定量分析，结论如下：（1）仿真与测试结果均表明，通过振动幅值能量和能量传递损耗率指标，可以定量分析齿轮箱内部冲击振动在各界面之间的传播与衰减情况。（2）箱体内部的冲击振动沿不同传播路径的能量衰减率是不同的，其中在同一构件内部的能量传递损耗率较小，一般不超过5%。（3）内部冲击振动的大部分能量均损耗在传递路径中的第一个交界面处，其能量传递损耗率可达（70～80）%；位于啮合面两侧的大、小齿轮上的点，尽管距离接近，但能量衰减也超过70%；而当内部冲击振动传递到箱体上，总的能量损耗率可达98%。

［1］A.Kahaman.Effect of axial vibrations on the dynamic of helical gear pairs［J］.ASME Journal of Vibration and Acoustics，1993，115（1）：33-38.

［2］Jean-Luc Dion.Sylvie Le Moyne.Gear impacts and idle gear noise：experimental study and non-linear dynamic model［J］.Mechanical Systems and Signal Processing，2009.23（8）：2608-2628.

［3］RAJENDRAN R，NARASIMHAN K.Linear elastic shock response of plane plates subjected to underwater explosion［J］.International Journal of Impact Engineering，2001，25（5）：493-506.

［4］邵毅敏，陈再刚，周晓君.冲击振动能量通过“齿轮-轴-轴承-轴承座”多界面传递损耗研究［J］.振动与冲击，2009，28（6）：60-65.（Shao Yi-min，Chen Zai-gang，Zhou Xiao-jun.Study on decaying of shock vibration energy during transmission through multi-interfaces in gear-shaft-bearing-housing system［J］.Journal of Vibration and Shock，e-guang，2009，28（6）：60-65.）

［5］李润方，林腾蛟，陶泽光.齿轮箱振动和噪声试验［J］.机械设计与研究，2003，19（5）：63-65.（Li Run-fang，Lin Teng-jiao，Tao Ze-guang.Study on vibration and noise test for gearbox［J］.Machine Design and Research，2003，19（5）：63-65.）

［6］许洪斌，吴灿元.大型风电齿轮箱耦合固有特性仿真分析［J］.机械设计与制造，2014（5）：192-194.（Xu Hong-bin，Wu Can-yuan.Simulation and analysis of coupled natural characteristicof largewind-turbinegearbox［J］.MachineryDesign&Manufacture，2014（5）：192-194.）

［7］石万凯，郑站强，李学明.风电齿轮箱动态响应分析级实验测量［J］.机械设计，2012，29（4）：63-67.（Shi Wan-kai，Zheng Zhan-qiang，Li Xue-ming.Dynamic response analysis and experimental measurements of wind turbine gearbox［J］.Journal of Machine Design，2012，29（4）：63-67.）

［8］雷亚国，汤伟，孔德同.基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断［J］.机械工程学报，2014，50（17）：61-68.（Lei Ya-guo，Tang Wei，Kong De-tong.Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis［J］.Journal of Mechanical Engineering，2014，50（17）：61-68.）

［9］王峰，方宗德，李声晋.人字齿轮系统振动传递分析优化与试验验证［J］.机械工程学报，2015，51（1）：34-42.（Wang Feng，Fang Zong-de，Li Sheng-jin.Analysis optimization and experimental verification of herringbone gear transmission system［J］.Journal of Mechanical Engineering，2015，51（1）：34-42.）

［10］李文昌.基于振动信号传播路径的齿轮箱振源检测系统研究［D］.杭州：杭州电子科技大学，2013：9-19.（Li Wen-chang.Vibration source detection system of gearbox based on vibration signal propagation path［D］.Hangzhou：Hangzhou Dianzi University，2013：9-19.）