化错:从诊断学生的真实错误开始

摘要:“化错”就是变化错误,帮助学生走向正确的学习道路。精彩的“化错”教学更能体现一位教师的教学智慧,体现教师面向全体的教育情怀。但现在一些看似“精彩”的化错教学,不是面对学生真实的错,而是来自书本的错和教师臆想的错,从而使化错失却了针对性。如何发现学生在学习中真实的错?课前进行学情调查、课中创设融错空间、课后建构合理的诊断系统,是一条行之有效的路径。
关键词:小学数学;化错 ;真实错误;诊断
中图分类号:G623.5 文献标志码:A 文章编号:1673-9094(2017)11B-0040-04
“化错”一词源自华应龙老师的“化错教育”。“化”指变化,“化错”就是变化错误,帮助学生走向正确的学习道路。一节真实的课堂,学生不可能不出现错误。如果说以前的课堂更多的是追求一种精致,一种滴水不漏般的正确,那么现在的课堂上老师们更乐意将错误转变成课堂的亮点。因为精彩的“化错”教学更能体现教师的教学智慧,体现教师面向全体的教育情怀。
当然,我们也看到,在一些日常课特别是公开课上,精彩的“化错”教学却忽略了真实的学习过程,而沦为一种重形式的作秀。
案例一:
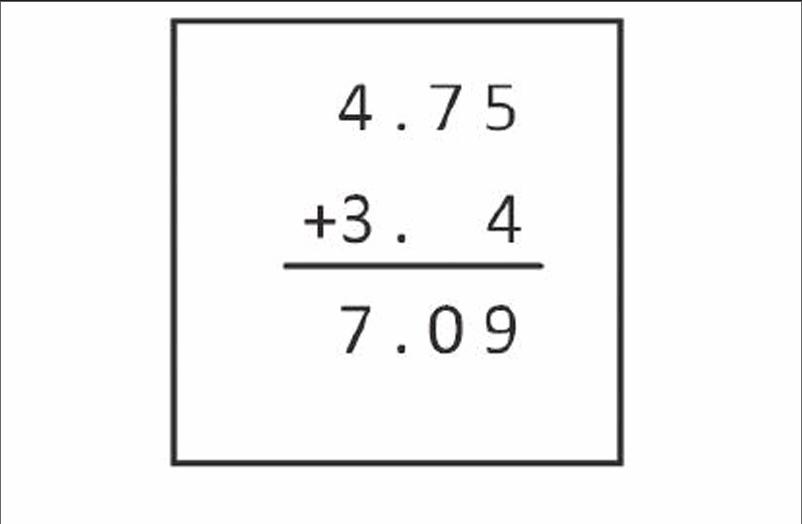
五年级上册《小数加减法》例1,创设情境后,教师安排学生尝试计算4.75+3.4,并在教材中出现了两种算法:
上一节课上,教师进行了“尝试计算—两种算法判断—比较说明算理”的教学过程。在交流环节,当学生讨论了第一种正确的做法后,教师反复问:“还有没有不一样的做法?”没有学生回答。一阵沉默后,教师拿出了书上的第二种错误的做法,说:“老师这里也有一种做法,大家一起来判断一下对不对。”学生一致回答:“错。”老师又问:“错在哪里呢?”学生说:“小数点没有对齐。”
一、化错:应该面对学生真实的错
我们来剖析一下上述案例,为什么教师会将不是学生“错误”的错拿来大做文章呢?
1.教材本位:书上的都是对的
我们现行使用的教材是由许多专家、经验丰富的教师和教学研究人员合作编写出来的,他们不仅谙熟我国数学课程的历史和现状,把握了新课标的要义,而且对国际数学课程发展的潮流有着相当深的理解和把握。对教师来说,教材是主要的教学资源,是教与学的重要依据。[1]因此,我们在教学前首先要认真钻研教材,吃透教材的编排意图,但这并不意味着就应该唯教材论。古人早就说过:尽信书,则不如无书。教材上出示的方法是具有代表性、典型性的方法,但不同地区、不同学校学生的多样性也使得教材不可能穷尽所有方法。教材本位主义者认为:教材就是标准,书上讲的方法就一定要展示,书上的错误就是学生的代表性错误,即使学生没有出现这类错误,也一定想办法出示。正如“案例一”中的那样,学生没有这类错误,教师自己就拿出来,或课前约定让学生故意犯这类错误,或假意说隔壁班有同学这样做的。因为不是来自学生出现的真实的错误,纠错便缺失了针对性,学生参与意识不强,刻意编制的错误反而影响了他们已有的正确认知。而且,因为教师只想强调书上这种典型错误,反而忽略了学生产生的真实错误。如上述案例中,笔者听课时坐在旁边的小男生是这样做的:
当老师首先展示正确的做法后,这位同学意识到了自己的错误,所以老师反复问还有没有不同的做法时,他不敢展示自己错误的做法了。如果教者能够在钻研教材的同时,理清本节内容在小学数学教学中所处的位置,就会发现:没有发生书上的典型错误是很正常的。追溯学生对小数的认识过程就可以发现,他们在三年级下学期已初步认识小数,并学过用竖式计算一位小数的加减法。在当时的教学中,虽然没有完整概括小数加减法的计算法则,但稍有数学知识的教师都会强调列竖式时“小数点对齐”,而不会说成“只要末尾对齐”。因为,老师们都知道,三年级只学一位小数的加减法,“小数点对齐”和“末尾对齐”虽是一回事,但为了与后续学习相衔接,都会强调“小数点对齐”。因此,到五年级再次学习“位数不同的小数加减法”时,学生也能正确地迁移“小数点对齐”的算法,只是对于“为什么小数点对齐”却一知半解 [2] 。基于以上分析,学生对“小数点对齐”的算法并非一无所知,反而是早已熟悉,这也就是导致他们没有出现书上典型错误的主要原因。
2.教师本位:“我”想的就是学生想的
對学生错误的精彩转化,有时来自教师长期积累的教学智慧,但更多的来自教师课前充分的预设。尤其在尝试教学、探究性学习时,常常需要根据以往的教学经验猜测学生可能出现的种种生成情况,包括可能出现的各种错误。经验丰富的教师一般猜得很准确,但既然只是一种课前预想,那么学生的课堂生成有可能在意想之中,也可能是意料之外。如“案例二”中,教师想通过展示错误的做法引起学生的注意:异分母分数加减法不可以将分子、分母分别相加,而应该寻找新的方法解决,并且学会从结果来估计结果的正确性。教师在巡视后发现没有这种预设中的错误,只好自己出示这种错误请学生辨析。那么,学生为什么不会出现这类错误呢?在学习异分母分数加减法前,他们学过了同分母分数加减法,教学时,教师往往会问:“同分母分数加减法,为什么分母不变,只要将分子相加减呢?”学生就理解了其中的道理:分母相同,是分数单位相同,也就是每一份的大小相同,只要将分子所代表的份数直接相加。当学生遇到异分母分数加法时,首先会和同分母分数加法作比较,思考如何把分母也变成相同的,再用学过的知识来解决新问题。而教师出示的错误,只有对分数的意义和同分母分数加减法完全不懂的人才会这样盲目相加。教师本位主义者在教学时常以教案为中心,以自己所想代替学生所想,认为凭经验预想的就是学生会出现的情况,所以当学生的生成在意料之外时,仍然拘泥于教案设计,把教师臆想的错误当成学生的错误。
二、化错:如何发现学生真实的错
学生学习中的“错”可以生成新的学习资源,应该已成为大家的共识。但这种“错”应该是来自学生真实的“错”,而不是书本上的错,更不是老师臆想中的错。只有面对学生真实的“错”,进行适切的转化和提升,才能有助于学生数学知识的掌握、数学能力的提升。endprint
如何发现学生真实的“错”呢?
1.基于调查的学情分析,预设潜在错误
美国心理学家奥苏伯尔在其著作《教育心理学》中写道:“如果我不得不把全部的教育心理学还原为一句话,我将会说,影响学习的唯一的、最重要的因素,是学生已经知道了什么,我们应当根据学生原有的知识状况去进行教学。”因此,我们在设计教学方案前,有必要通过调查,全面了解学生的所知、所惑、所错,所需。其中很重要的一点,就是通过调查了解学生学习新知可能出现的典型性错误,使教者心中有数,应对有底。如“案例一”中,教師可以在课前选取各层面有代表性的学生若干,在没有任何提示的情况下尝试用竖式计算一道小数加减法,了解学生可能的解法,并通过对话的方式询问学生这样计算的想法。如果这些代表学生中没有出现书上典型的错误,教师就要思考“为什么”了。这样提前思考,就可能避免课堂上生硬地展示“错误”。同时,通过这样的课前调查,还可以发现学生的其他错误算法和想法。
课前调查除了分层抽样,还可以整体抽样,采用的方式一般是问卷或访谈。如一位老师在上“角的初步认识”时设计了如下问卷题:(1)你能在生活中找到角吗?(2)角是怎样的?请你画下来。调查后发现对于问题(1), 96.3%的同学能找到生活中的角,但50%左右的学生找的不是数学意义上的“角”,而是房间的角落、几何体的顶点等等,说明学生还不能区别生活中的“角”和数学上的“角”。根据学生的这一错误认识,教学时就要突出将生活中物体面上的角抽象的过程。抽象之后,还要引导学生正确地指一指,比较这些抽象出的图形的共同特征,从而使学生形成对数学上“角”的正确认识,以区别生活中的“角”。经过调研之后的教学设计,能针对学生的真实潜在问题展开教学,使“化错”更有实效。
2.创设容错的学习空间,发现生成错误
差错在课堂中无时不在,但部分教师害怕出差错,一味去堵,去回避,学生真正的生成性错误就无法展现。在有容错空间的课堂上,孩子们不怕出错,他们享受错误,懂得“错误是创造的开始”,所以当他们出错了,也敢于展示自己的错误,说出自己错误背后的真实想法,更敢于自我纠错。因此,创设容错的学习空间,教师应有容错的雅量和情怀,认识到“自古成功在尝试”,让孩子们试错,其实就是在尝试,在求真,坦然面对学生的错误,才有可能机智地进行点化。
首先,教师要有发现错中蕴藏着亮点的眼光。例如有位老师在上二年级《角的认识》一课时,出示两个角让学生尝试判断哪个角大,哪个角小。老师问:“你们可以用什么工具来比较这两个画在黑板上角的大小呢?”一位同学高举着小手抢着说:用尺量。老师很惊奇,让这位同学上台演示。这位同学将长尺对准角两边画的端点处,量了两端点之间的距离。虽然他的办法是错的,但老师还是微笑着对他和同学们说:“我们量长度是用尺子量,他想到量角的大小也可以用尺子,其实是想用尺来量出角的两边叉开的大小。角两边叉开的大小决定了角的大小,我们手边的哪个工具更容易量出这两个角的边叉开的大小呢?”学生自然就想到了活动角。在这里,虽然学生的量法是错误的,但老师独具慧眼,敏锐地捕捉到错误中的“正确”因子,引领学生继续走向学习的关键之处。
其次,教师要给予学生改错的机会。例如在教学“万以内数的读法”一课,当学生根据计数器写出3052这个数时,小朱同学读成了“三千五十二”,立刻被同学们的反对之声淹没。他也意识到可能是自己读错了,涨红着脸坐了下去。我不置可否,继续请另一位小陈同学读。我转向小朱,问:“听出你俩读法上的不同之处了吗?”小朱说,小陈读出了零,他没有读出中间的零。我表扬他善于倾听后继续问:“读三位数时,中间的零要读吗?”他肯定地点点头。“对了,这里的四位数中间有0,也要读。”我接过话,并请他再读一遍,他声音响亮地读对了。我转向全班同学说:“看,学习就是不断纠正错误的过程,今天小朱同学又学到新知识了,那就是读四位数时中间的0……”同学们齐声说:“也要读。”这时,再看小朱同学,他再也没有了刚才的窘迫。正是因为教者有容错的雅量和情怀,知道每个学生有不同的学习起点,学生的错误也许五花八门,但老师面对学生的态度却是一样的和蔼、一样的温暖、一样的鼓励。正是这份情感的投入,才能使学生敞开心扉,展示自己真实的错误,不以错为耻,在错误中不断探索,不断前进。
3.构建合理的诊断体系,掌控既成错误
通过课堂练习,教师更能够发现学生真实的错误,但并不是所有的真实错误都能在做练习时准确反映出来的。如教学平行四边形面积的计算后,老师会出示一些明确了底和高的平行四边形,请学生计算面积。学生可能都做得对,但有一部分并没有完全理解为什么这样算,只是照搬公式,模仿而已。再如,一些老师喜欢在课上听学生齐答,看似异口同声、完全正确,其实一部分学生却在滥竽充数。还有,一些练习采用指名口答的方式,却常常成了一部分思维迅速学生的表演等等。如此的课堂诊断,并不能让老师真正了解学生的真实错误,因此,化错、纠错的针对性也就无从谈起。
笔者认为构建合理的诊断体系很重要,这种体系主要包括诊断内容和诊断方式两大方面。
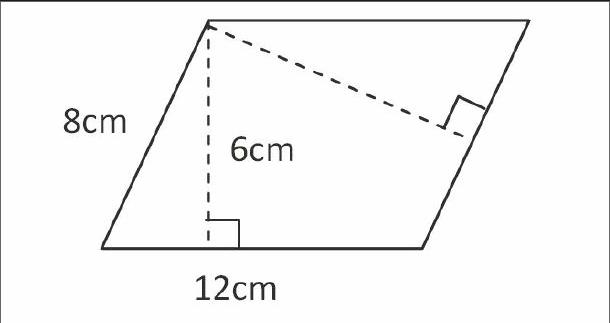
一是诊断内容要全面。既要考查学生对本课知识和技能的掌握情况,又要考查学生在学习过程中获得的能力、方法,甚至能诊断出学生的学习态度和习惯。例如,出示:
提问学生:“怎样计算平行四边形的面积?为什么?”面对此题,如果学生出现8×12的错误,说明他还没有理解平行四边形面积的推导道理;如果出现8×6的错误,说明他不知道平行四边形面积计算中,底和高应该是一组对应的数量。而如果学生说不出“为什么这样计算”,说明他只是机械地模仿。多了解一些信息,对学生学习情况的诊断就更全面了。
二是诊断方式要多样。课堂上我们通常会采用独立练习、口答、齐答等方式进行诊断,这些各有利弊。教学中应灵活运用多样诊断方式,既有指名口答,也有独立练习,要增加学生独立思考的时间,使不同的学生能够较充分地展示自己的思考过程。要面向全体学生,有针对性地关注不同层次的学生。要多倾听学生陈述想法,当堂访谈或课后访谈,以便了解错误背后真正的原因。
学生学习中产生的不可避免的错误,是一种新的学习资源。作为教师,应该正确面对学生真实的错误,包容理解学生真实的错误,智慧化解学生真实的错误,真正达到化错育人的学习效果。
参考文献:
[1]吴文娟.给创造性使用教材提个醒.小学教学参考[J],2008(7).
[2]吴文娟,俞昭英.“按图索骥”还是“顺势而为”.中小学数学(小学版)[J], 2013(8).
责任编辑:宣丽华
Abstract: Mistake-changing means changing the types of mistakes to help student take the right way of learning. Excellent mistake-changing teaching can better display teachers teaching wisdom and their educational feelings. Yet, seemingly excellent mistake-changing instruction is not oriented towards students real mistakes but mistakes from textbooks and teachers imagination, which results in absence of targeted mistakes. An effective way of finding students mistakes is to pre-class diagnosis of learning, while-class designing room for mistakes, and post-class construction of diagnosing systems.
Key words: primary school mathematics; mistake-changing; real mistake; diagnosisendprint

