广义草莓蚜虫生态系统模型的分析与控制
索宇航,刘敬娜,赵立纯,尹振雪,高亚珍
(1.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007;2.辽宁科技大学 理学院,辽宁 鞍山 114051)
为害草莓的蚜虫有多种,以桃蚜、棉蚜为主,其传播草莓病毒使草莓产量减少,给种植者带来重大经济损失[1]。由于草莓蚜虫繁殖快,蔓延迅速,必须及时防治。为此在实际生产中,一般采用以喷洒杀虫剂为主的化学防治,不仅对环境造成污染还会降低草莓品质[2-3],因此需要环保的控制措施,如以投放瓢虫、草蛉、食蚜蝇、蚜茧蜂等天敌为主的生物防治[4]。结合生物防治在虫害爆发前预防效果好的特点,设计科学合理的控制策略是对蚜虫类害虫进行有效防控的关键问题,也是值得进一步探讨的问题。
目前,关于草莓蚜虫病的防治问题多采用定性研究方法,受种植者的经验影响,有一定的盲目性。为了定量研究蚜虫类害虫的防控问题,了解其种群的动态规律也很重要。近年,一些学者将以折叠突变模型为基础的多种突变模型应用到蚜虫生态系统中,不仅成功刻画其种群爆发的发生发展规律,还分析出蚜虫类害虫生态系统具有双峰性、不连续性(突变性)、滞后性和发散性等基本突变性质[5-6]。而这些突变性质还可以利用广义系统模型特有的脉冲行为刻画。一般来说,广义系统模型在揭示和预测被调查系统的动态特性方面具有重要优势,对生物生态系统的建模、分析和控制产生了巨大的影响,并且获得一系列重要研究成果[7-10]。文献[11-12]关于广义系统向前/向后障碍点的定义、判定和特性的研究是运用广义系统特有的脉冲行为刻画蚜虫种群突跳的基础与有力工具。但是这些研究均以单纯微分方程表示的系统动态出发,附以由代数方程表示的静态限制来建立广义生物系统模型,没有将刻画系统突变性作为建模的重点。有鉴于此,本文基于代数方程表示的生态系统的静态行为,即突变流形,结合微分方程表示的动态描述构建广义系统模型。
1 模型建立
基于Logistic模型Holling II功能反映函数,考虑天敌胁迫下草莓蚜虫种群的折叠突变模型[13]
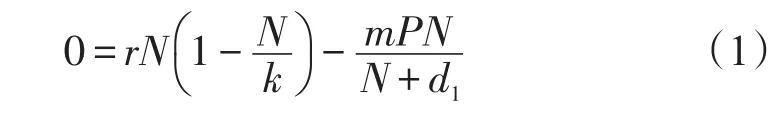
式中:N,P分别为草莓蚜虫种群密度及其天敌种群密度;r,k分别为草莓蚜虫种群的内并增长率和环境容纳量;m为天敌种群对草莓蚜虫种群的捕获效率;d1为由天敌种群引起蚜虫种群的死亡率。
模型(1)通过坐标变换可化为标准的折叠突变模型,其草莓蚜虫种群密度随着天敌种群密度从小到大连续变化会出现突跳现象[5-6]。实际上,天敌种群密度是随时间有规律变化,考虑到食饵草莓蚜虫种群的影响,天敌种群密度的变化率可用微分方程描述
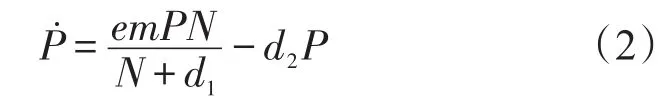
式中:e为草莓种群转化为天敌种群的转化率;d2为天敌种群的死亡率。
耦合模型(1)和模型(2),得到一个广义草莓蚜虫生态系统模型
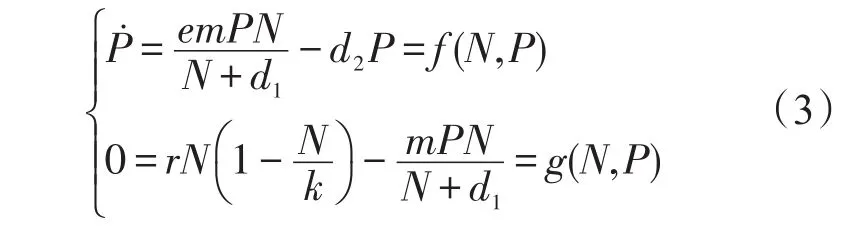
式中:r,m,k,d1,d2和e的定义如上且均为正常数。
根据生态意义,随后关于广义系统模型(3)的定性分析和控制器设计都在区域D={(P,N)|P≥0,N≥0}上进行讨论。
2 定性分析
为了探讨模型(3)复杂动力学行为,首先根据文献[11]中的定义给出如下三类点集及相应结论。
(1)平衡点

其中:点M3是PON平面上抛物线和直线的交点。
定理1 当且仅当em-d2>0,k(em-d2)-d1d2>0时,模型(3)存在正平衡点。
在定理1基础上,根据广义系统平衡点、奇异点和障碍点的特点和性质[12],利用几何分析方法,得到如下定性分析结果。
定理2 对于模型(3):
1和M2,且均为稳定结点,而点S2为向后障碍点,见图1a;
1和M2,且点M1为稳定结点、点M2为鞍点,而点S2为向后障碍点,见图1b;
从上述定性分析可得两个重要结论,一是若点S2为向前障碍点,则系统到达此点会出现突跳(脉冲)现象,系统瞬间从点S2落到P轴上,再稳定于稳定平衡点M1;二是若平衡点M3存在且落在点S2的上方,则其为稳定平衡点,那么以点S2的上方任何点为初始状态,系统最后都会稳定在草莓蚜虫种群密度较高的点M3,这不是人们期望看到的,也是本文要施加人工干预的情况。
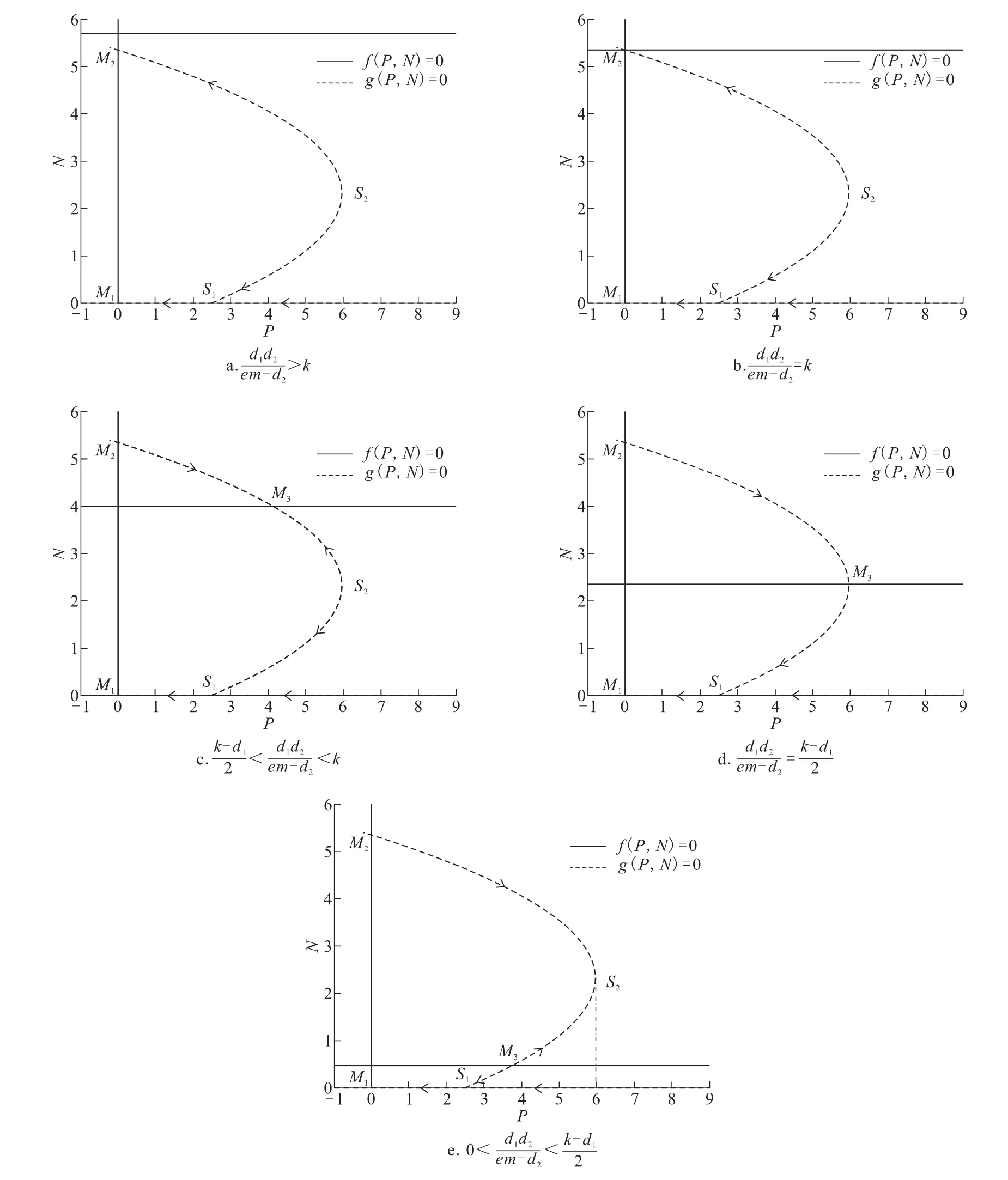
图1 定理2的几何分析图Fig.1 Geometric analysis figure for theorem 2
3 控制器设计
针对平衡点M3存在且落在点S2的上方的情况,不失一般性,在点M3下方取初始点,其种群密度的时间响应见图2a,以蚜虫种群密度较低的曲线段S1S2为控制目标,采用投放天敌种群的手段,建立草莓蚜虫控制模型
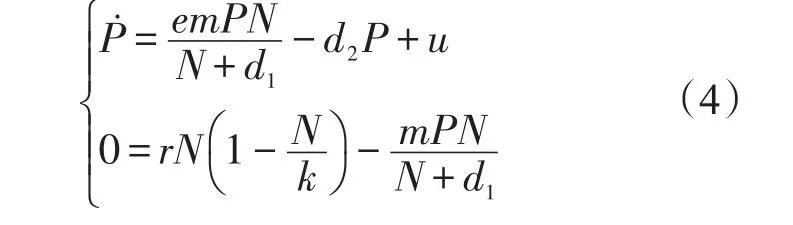
式中:u为控制输入量,也是投放天敌总量,且u≥0。
考虑控制器结构简洁、控制措施易于实现等问题,设控制输入量仅与当前天敌种群密度相关并取线性形式,则取
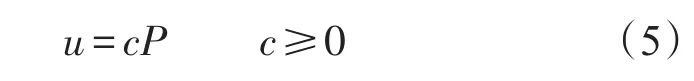
为了实现控制目标,即施加控制后,抛物线与直线的交点在曲线段S1S2上,为此令
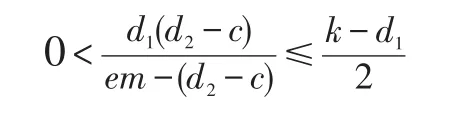
图2a是控制实施前模型(4)的时间响应图,图2b~图2d是不同控制强度下模型(4)的时间响应图。在控制器(5)作用下,系统从蚜虫种群密度较高的状态稳定于蚜虫种群密度较低的状态,可以保证草莓的产量和品质。与图2c~图2d对比,图2b给出了一种较特殊的情况,即避开了系统的障碍点。此时投放天敌的强度不够大,虽然可使系统最终停留在蚜虫种群密度较低的状态,但用时较长可能错过了草莓的采摘期。通过比较图2c与图2d,可以看到投放天敌的强度越大,蚜虫种群密度下降越快,控制器的效果越明显。
与文献[13]的研究结果相比较,本文所建广义系统模型的数值模拟结果,即图2c~图2d显示的蚜虫种群密度随天敌种群密度的连续变化而出现的骤降现象,更准确地刻画了蚜虫生态系统的突变现象,且与实际数据更相近。
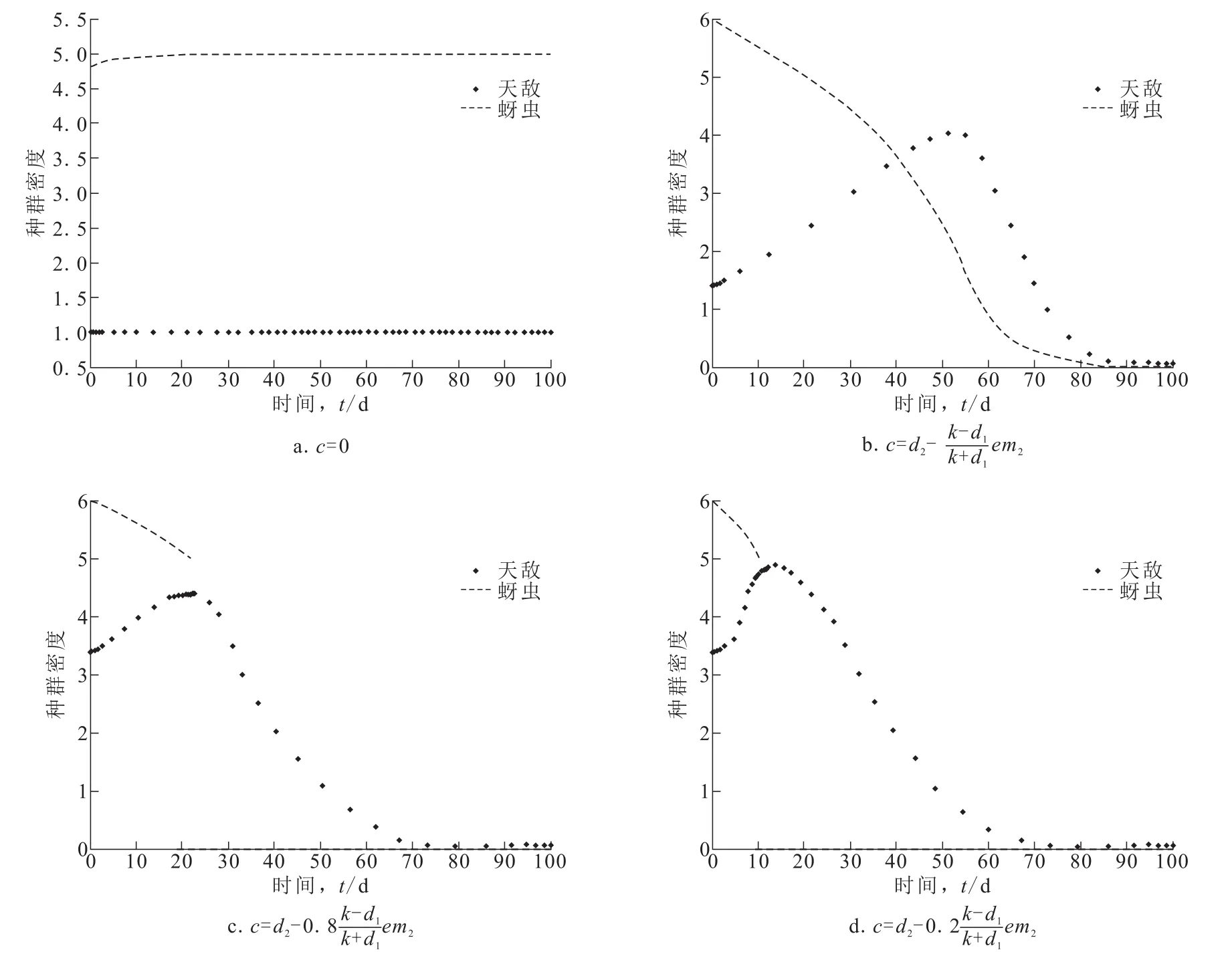
图2 模型(4)的时间响应Fig.2 Time response of model(4)
4 结论
本文首先基于草莓蚜虫生态系统折叠突变流形,考虑其中有关天敌种群参数的变化率及其对蚜虫种群的作用,提出一个广义系统模型。其次,结合广义系统理论和突变理论,通过几何分析方法对草莓蚜虫生态系统进行了定性分析,探讨其复杂动态行为及相应的生态学机制。最后,针对蚜虫种群密度较高的情况,采用投放天敌的控制手段,设计控制器使系统稳定于蚜虫种群的避难状态,并通过数值模拟验证了控制器的效果。在控制器有效约束条件下,通过逐步增加控制力度的方式,进一步验证了控制器的效果随着天敌投放力度的增加而明显增大,这与实际情况的研究相符。
[1]廖建明.草莓蚜虫的发生规律与防治对策[J].北方农业学报,2007(1):111-112.
[2]马俊岭,杨宝东,张志勇,等.啶虫脒防治草莓蚜虫的残留动态及膳食风险评估[J].农药,2014,53(5):346-349.
[3]吴声敢,苍涛,柴伟纲,等.草莓蚜虫防治药剂筛选试验[J].浙江农业科学,2016,57(12):2048-2050.
[4]焦雪霞,贾茜,杨金利,等.异色瓢虫防治菜花蚜虫效果试验[J].生物技术进展,2016,6(3):224-226.
[5]闻飞祥.草莓种群生态系统T-S模糊模型的建立与控制[D].辽宁科技大学,2016.
[6]JONES D D.Catastrophe theory applied to ecological systems[J].Simulation Transactions of the Society for Modeling and Simulation International,1977,29(1):1-15.
[7]ZHAO F,ZHANG Q,YAN X,et al.filtering for stochastic singular fuzzy systems with time-varying delay[J].Nonlinear Dynamics,2015,79(1):215-228.
[8]ZHANG Q L,YANG D M.Analysis and synthesis of uncertein singular system[M].Shenyang:Northeastern University Press,2003:88-92.
[9]YANG D M,ZHANG Q L,YAO B.Singular System[M].Beijing:Science Press,2004:115-118.
[10]ZHANG Y,ZHANG Q,YAN X G.Complex dynamics in a singular Leslie-Gower predator-prey bioeconomic model with time delay and stochastic fluctuations[J].Physica A Statistical Mechanics&Its Applications,2014,404(24):180-191.
[11]CHUA I O,DENG A.Impasse points.Part I:Numerical aspects[J].International Journal of Circuit Theory&Applications,2010,17(2):213-235.
[12]CHUA L O,DENG A C.Impasse points.II.Analytical aspects.[J].International Journal of Circuit Theory&Applications,2010,17(3):271-282.
[13]赵学达,赵惠燕,刘光祖.天敌胁迫下食饵种群动态模型的突变分析[J].西北农林科技大学学报,2005,33(4):61-64.
——管氏肿腿蜂的应用技术

