中考几何压轴题有效教学的点滴做法

广东省广州市荔湾区美华中学(510160) 郑燕

一、问题提出

中考几何压轴题是必考题目,近八年广州市中考题中几何压轴题的得分都在3分左右,老师和学生都感觉到花了很多时间和精力、讲解和练习了很多题目,但收效不高.多数学生在解题时,连题目都没有信心看下去,或者即便是能看懂问题,但面对图形无从下手,最后放弃思考.所以一般生源的学校往往会放弃这类题目的解题教学,反复操练代数运算的题目,以提高考试的平均成绩.以下是2008年—2016年广州市中考几何压轴题得分情况：

年份2008年2009年2010年2011年2012年2013年2014年2015年2016年题号24 24 24 25 25 24 25 24 25该题满分14 14 14 14 14 14 14 14 14全市平均分4.09 2.43 2.78 2.62 2.72 3.74 1.99 2.46 1.73

二、归因分析

1.思维训练欠缺.

新课教学中,教师不注重展示知识生成的过程,匆匆讲授完定义、定理和例题后,就进入机械训练,不注重渗透核心数学思想方法,较少进行“一题多解”的教学,其结果就是学生知其然不知其所以然,思维训练欠缺.备考复习时,因为部分学生学业水平不高,教师放弃讲解这类题目,或者仅仅是大量练习,但没有对学生进行“多题归一”的指导.

2.解题信心不足.

师生双方都对解决压轴题缺乏信心.对中等或以下水平的学生,教师往往要求他们不要关注压轴题,只要做好基础题就可以了,这部分学生由于缺乏自我认同感,也就渐渐放弃去看压轴题了.中考平均分显示,相当部分学生没有去完成压轴题中前面较基础的问题.

3.阅读理解不清.

中考压轴题的字数在200字左右,文字量大,其中还有不少几何符号,即便学生有意愿去尝试解决压轴题,但由于阅读起来存在困难,更不用说理解其中的含义了,所以也造成学生放弃解决压轴题.以下是近九年中考几何压轴题的字数：

年份2008年2009年2010年2011年2012年2013年2014年2015年2016年题号24 24 24 25 25 24 25 24 25字数174 122 175 201 167 195 109 223 139

三、理论依据

1.学习心理方面

加涅认为,如果学习者对达到预定目标有强烈的愿望,即处在较高水平的动机状态,他就能集中注意,专心学习,选择行之有效的学习和记忆策略.学习目标的实现会令学习者感到满足、愉快,从而增强了学习信心,更加努力地投入下一个学习活动.

心理学研究发现,学习者遇到的新情境越复杂,新情境与原先学习的情境越不相似,问题解决的难度越大,所要求的创造性程度越高.创造是解决问题的最高形式.奥苏伯尔认为,解决问题涉及到问题条件命题和目标命题、背景命题、推理规则和解决策略.有意义学习必须具有三个条件：学习材料具有逻辑意义;学生认知结构中具有同化新知识的原有知识基础;将材料的潜在意义转化为学生心理意义的一个重要条件是学生具有有意义学习的心向.

中学阶段的思维能力既然是以逻辑思维能力的发展为基础和核心的,几何教学应更加强调对逻辑推理能力的培养,使学生能从已有的事实出发,凭借经验和直觉,通过归纳和类比等推测某些结果;并从已有的事实(包括定义、公理、定理等)出发,按照规定的法则证明(包括逻辑和运算)结论.在整个数学教学过程中发展学生的推理能力.

2.几何教学方面

《义务教育数学课程标准(2011年版)》中提出,数学是人类文化的重要组成部分,数学素养是现代社会每一个公民应该具备的基本素养.关于几何课程的目标要求是：掌握图形与几何的基础知识和基本技能,发展合情推理和演绎推理能力,清晰地表达自己的想法.

高慎英、刘良华著的《有效教学论》中指出：凡是能够有效地促进学生发展,有效地实现预期的教学结果的教学活动,都可称之为“有效教学”.

四、做法建议

(一)夯实基础

1.构建知识网络

《2016年广州市初中毕业生学业考试指导书》中明确了考查知识内容及考查目标要求,详细列举了基本事实与定理共23条,包含94个定理,作为计算或证明的依据.教学中,可以在初始年级指导学生利用思维导图构建知识网络图,到九年级时,就能形成一个完整的平面几何知识网络图.学生对图形的性质和判定有了清晰的认识与理解,有利于解决复杂的几何问题.核心知识点的生成过程不能忽略,分析讲解就是一种思考问题方式的展示.

2.熟悉基本图形

教材中的例题、习题的图形很多都是基本图形,中考几何压轴题的图形中往往是由一些基本图形叠加而成的.日常教学中,指导学生认真分析研究这些图形,真正理解图形中包含的信息,从而熟悉这些图形,有利于从压轴题的复杂图形中提取基本图形,找到解决问题的突破口.

(二)解题指导

1.尝试猜测联想

压轴题包含的信息比较多,而且图形复杂,解题时需要根据题意和图形猜测联想,多次尝试.日常压轴题的教学中,要鼓励学生根据题意大胆猜想,利用排除法进行筛选,找到解决问题的最佳路径.中考备考阶段,更要给学生足够的时间去尝试、猜想、论证,让学生享受探究的快乐.

2.合理添加辅助线

几何压轴题的图形比较复杂,基本上都需要添加辅助线才能解决问题.日常压轴题的教学中,要指导学生根据题意作图,重点分析辅助线添加的原因,合理添加辅助线.

3.观察提取基本图形

近年来,《广州市初中毕业生学业考试年报》的分析中多次提到,学生遇到难题畏缩,缺乏信心,题目中的条件不会转化,不会提取核心图形、典型图形,最后选择放弃解答.因此,日常压轴题的教学中,要学习根据题意画出图形,认真分析典型图形,指导学生在复杂图形中提取基本图形.

4.渗透数学思想方法

压轴题的教学,不是一蹴而成的事.从起始年级就应该渗透核心内容、数学思想方法.日常教学,注重分析知识的生成过程,真正指导学生理解核心内容、数学思想方法,学会将已知条件合理转化.解决问题时,学会适当引入参数,找等量关系得到方程求参数值,或通过化简消去参数以达到解决问题的目的.

5.总结提升多题归一

压轴题的教学,除了指导学生通过分析题意、转化已知、猜测联想、添加辅助线、提取基本图形、运用数学思想方法解决问题外,还要指导学生将所做过的压轴题进行分析总结,提炼出通性通法,实现“多题归一”.

(三)实例分析

1.下面以2016年广州市中考数学第25题(全卷最后一题)为例,说明如何通过猜测联想转化已知、添加辅助线、提取基本图形、合理运用数学思想方法,以解决问题的过程.

原题重现如图,点C为△ABD外接圆上的一动点(点C不在弧BAD上,且不与点B,D重合),∠ACB=∠ABD=45°.

(1)求证：BD是该外接圆的直径;

(2)连结CD,求证：;

(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.

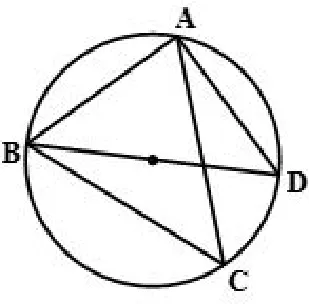
分析过程第(2)问,要证明,要用截长补短的方法,但有AC前有系数,截长不容易,所以想到补短.还要保留∠ACB=45°,所以,

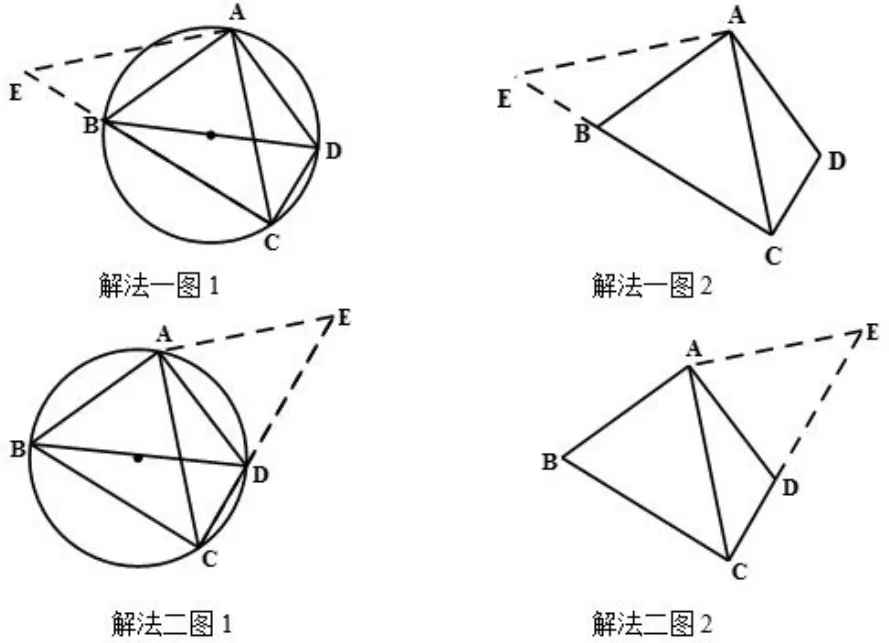
解法一如图1,选择延长CB到E,使BE=CD,则BC+CD=BC+BE=CE.需证明,会联想到等腰直角三角形,图中没有,但有∠ACB=45°,所以猜想证明△EAC是等腰直角三角形,使得.为了证明AE=AC且∠EAC=90°,需证明△AEB与△ACD全等,这两个三角形就是常见的基本图形,如图解法一图2.

解法二如图2,选择延长CD到E,使DE=BC,则CD+BC=CD+DE=CE,需证明,会联想到等腰直角三角形,图中没有,但有∠ACB=45°,∠ACE=45°,所以猜想证明△EAC是等腰直角三角形,使得.为了证明AE=AC且∠EAC=90°,需证明△ABC与△ADE全等,这两个三角形就是常见的基本图形,如图解法二图2.

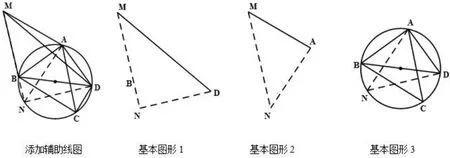
第(3)问,要探究DM2,AM2,BM2三者之间满足的等量关系,即探究三条线段长度的平方之间的关系,首先会联想到直角三角形.但这三条线段并不在一个直角三角形中,由图观察可以看到DM是最长的一条线段,所以尝试保留DM、BM,会选择延长线段MB(可以让学生尝试延长MA,看看是否可行),交圆于点N,由BD是直径,可以得到 ∠BND=90°,则MD2=MN2+ND2.由△ABC关于直线AB的对称图形为△ABM可得∠AMB= ∠ACB=45°. 由 ∠ABD=45°,可以得到弧AB所对圆周角都为45°,选择连接AN,得到∠ANB=45°,从而得到等腰直角三角形AMN,MN2=2MA2.则MD2=MN2+ND2=2MA2+ND2.最后就要分析ND与MB的关系了.由对称性得到MB=BC,所以转化为分析BC与ND的关系,在圆中分析弧BC与弧ND的关系,易证明弧BC=弧ND.从而问题得解.

2、总结提升,多题归一.下面以2008、2012、2016年广州市中考数学题为例进行分析.

原题重现

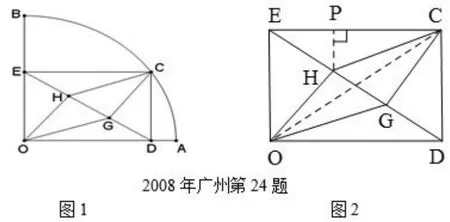
(2008年广州第24题) 如图1,扇形OAB的半径OA=3,圆心角 ∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE.

(1)求证：四边形OGCH是平行四边形.

(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度.

(3)求证：CD2+3CH2是定值.

(2012年广州第25题) 如图1,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点.CE⊥AB于点E,设 ∠ABC=α(60°≤α＜90°).

(1)当α=60°时,求CE的长.

(2)当60°≤α ＜90°时,

①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.

②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.

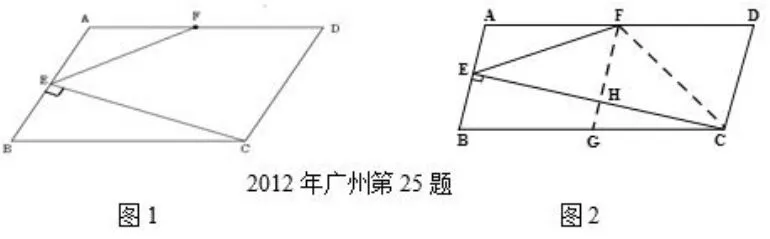
分析过程这三年的几何压轴题都出现了线段的平方,2008年较直观,直接证明“CD2+3CH2是定值”,2012年是“当CE2-CF2取最大值时,求tan∠DCF的值”,需要先求出线段平方差的最大值,2016年是“试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论”.虽然提问方式不同,但解决问题的思路都是找相应的直角三角形,这些边是直角三角形的边,如果没有符合条件的直角三角形,就需要根据题意构造直角三角形.辅助线添加如图所示(2008年广州第24题图2、2012年广州第25题图2、2016年广州第25题第(3)问添加辅助线图).因此,建议教师及时指导学生将题目归类,总结分析解决问题的通性通法,实现多题归一.

五、结束语

几何教学的目标是培养学生掌握图形与几何的基础知识和基本技能,发展合情推理和演绎推理能力,清晰地表达自己的想法.在平时的教学中要帮助学生树立解题信心,指导学生构建知识网络图,熟悉教材中的基本图形.压轴题的设问是层层递进的,点拨学生在解题中大胆猜测联想,合理添加辅助线,并提取基本图形,运用数学思想方法辅助解题.通过这样的指导,学生必能在几何的学习中提升推理演绎能力,尝到成功解决问题的快乐!