巧用延伸性知识 代数法妙解几何题

浙江省宁海县星海中学(315600) 李咪丽

在近几年的中考试题中,经常会涉及延伸性知识.这里的延伸性知识是指现行初中数学教材中没有直接出现的知识,包括公式和结论.本文将结合课堂教学实践阐述一些较实用的延伸性知识以期用代数法快捷、高效地解决几何问题.

一、巧用“平行四边形顶点坐标公式”妙解平行四边形存在性问题

1.公式阐述

(1)线段中点坐标公式

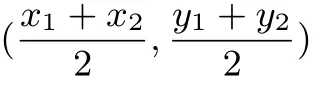
图1

证明如图1所示,设线段AB的中点P坐标为(xP,yP).易构造得△APC∼=△PBD,

则AC=PD,PC=BD

即xP-x1=x2-xP,yP-y1=y2-yP.

(2)平行四边形顶点坐标公式

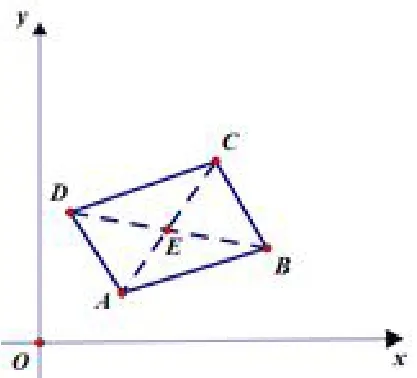
图2

证明如图2,设平行四边形ABCD的顶点坐标分别为A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD).连结AC,BD交于点E,由平行四边形性质可得对角线AC,BD互相平分,即点E既是线段AC的中点也是线段BD的中点.由线段中点公式可得E点坐标为

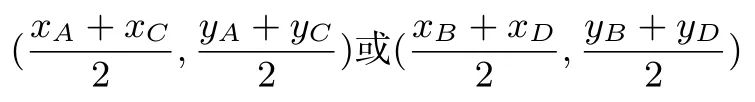
故有结论：xA+xC=xB+xD,yA+yC=yB+yD.即平行四边形对角线两端点的横坐标、纵坐标之和分别相等.

2.实例解析

例1如图3,在平面直角坐标系中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.

图3

分析平行四边形的存在性问题,常规解法是先画出平行四边形,再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先画出草图,若考虑不周,很容易漏解.而利用“平行四边形顶点坐标公式”就无需画出平行四边形草图,只要合理分类、有序组合,从对角线入手就不会漏解.这种方法条理清晰,而且适用范围广.解答过程如下：

解易得A(-1,0),B(3,0).

由题意可设P(0,m),M(x,-x2+2x+3).

①当AM,PB为对角线时,根据公式可得点A、M与点P、B的横坐标、纵坐标之和分别相等.

故M1(4,-5).

②当AP,MB为对角线时,根据公式可得点A、P与点M、B的横坐标、纵坐标之和分别相等.

故M2(-4,-21).

③当AB,PM为对角线时,根据公式可得点A、B与点P、M的横坐标、纵坐标之和分别相等.

故M3(2,-3).

综上所述,点M坐标分别为M1(4,-5),M2(-4,-21),M3(2,-3).

二、巧用“k1·k2=-1”妙解两直线垂直问题

1.结论(公式)阐述

(1)结论：已知直线y1=k1x+b1,y2=k2x+b2,若两直线互相垂直,则k1·k2=-1.

(2)k的计算公式

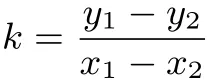
证明将点(x1,y1),(x2,y2)代入y=kx+b

两式作差得y1-y2=kx1-kx2,

2.实例解析

例2如图4,已知直线m:y=2x+1,分别交x轴、y轴于A、B两点.作点P(1,2)作关于直线m的对称点Q,求Q点坐标.

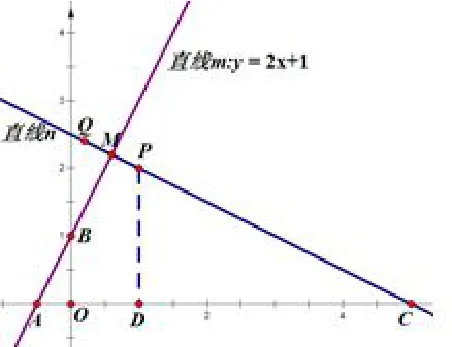
图4

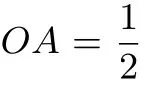
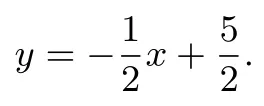
不难发现,常规解法虽然计算简单,但是构造相似这个思路学生很难想到,无形中加大了本题难度.而利用结论：两直线互相垂直,则k1·k2=-1则可快速、巧妙地解决该难点.

解设P、Q所在直线为直线n,直线n与x轴交于点C,两直线交点为M点.由对称性可得直线m⊥n,且点M为线段PQ中点.设直线n的解析式为y=kx+b.

由直线n⊥m得k1·k2=-1,即2·k=-1,

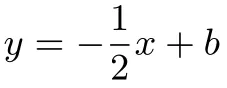
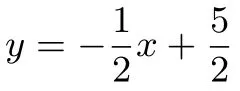
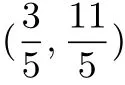
因为M是线段PQ的中点,且P(1,2),设Q(xQ,yQ)

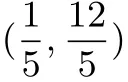
例3如图5,抛物线y=-x2+4x-3与x轴交于A,B两点(A在B的左边),与y轴交于点D.在抛物线上是否存在一点P,使得△BDP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.

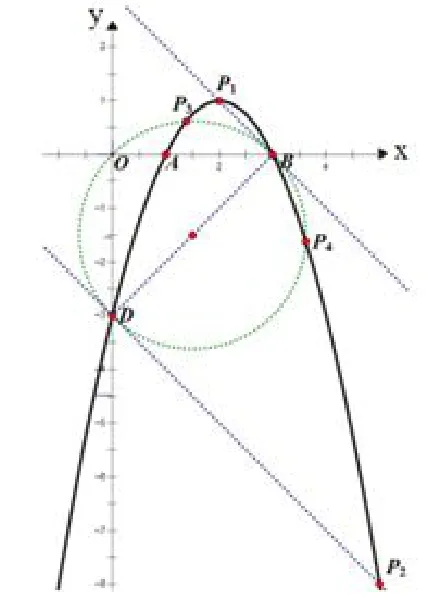
图5

分析以二次函数为载体的直角三角形存在性问题,因其图形复杂、知识覆盖面广、综合性强,近几年成为中考热点.此类题常规解法有两种：一是构造“双垂直”模型,再利用相似求解.这种方法难点在于构造“双垂直”模型,优点是计算简单.二是先利用两点距离公式表述出三条边,再利用勾股定理求解.这种方法是思路简单好想,但计算复杂,很容易出现四次项、三次项.而利用“两直线互相垂直,则k1·k2=-1”可以规避这些难点.

解易求得A(1,0),B(3,0),D(0,-3)

因为点P在抛物线y=-x2+4x-3上,故设点P(m,-m2+4m-3).则

分三种情况讨论：

①以点B为直角顶点,即BD⊥BP,

故有kBD·kBP=-1.

化简得m2-5m+6=0,

解得m1=2,m2=3(与B重合,舍去),

故P1(2,1).

②以点D为直角顶点,即BD⊥DP,

故有kBD·kDP=-1.

化简得m2-5m=0,

解得m1=5,m2=0(与D重合,舍去),

故P2(5,-8).

③以点P为直角顶点,即BP⊥DP,

故有kBP·kDP=-1.

因为m-3/=0,m/=0,

所以(-m+1)(-m+4)=-1,

化简得m2-5m+5=0,

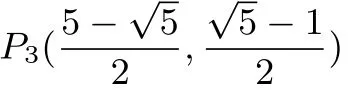
三、巧用“两点距离公式”和“点到直线距离公式”,妙解距离问题

1.公式阐述

(1)两点距离公式

已知A(x1,y1),B(x2,y2),如图6,则有AC=|x1-x2|,BC=|y1-y2|,,由勾股定理得.

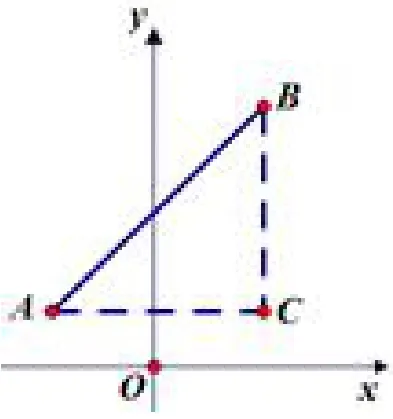
图6

(2)点到直线距离公式

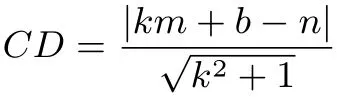
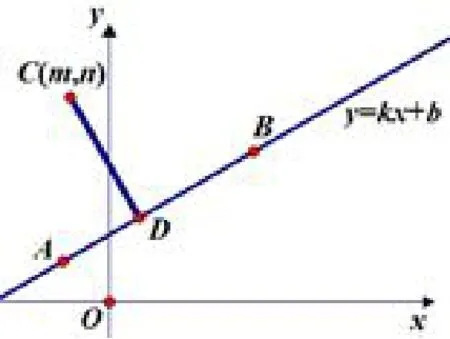
图7

证明由题意得CD⊥AB,则根据公式k1·k2=-1

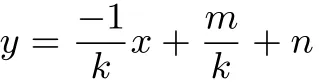
因为点D是直线AB与CD的交点,

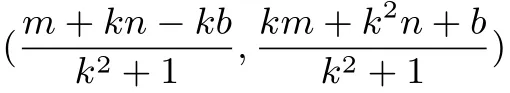
最后由两点距离公式可求得

2.实例解析

例4如图8,平面直角坐标系中,已知点A(1,3),B(3,5),C(5,4),求△ABC的面积.

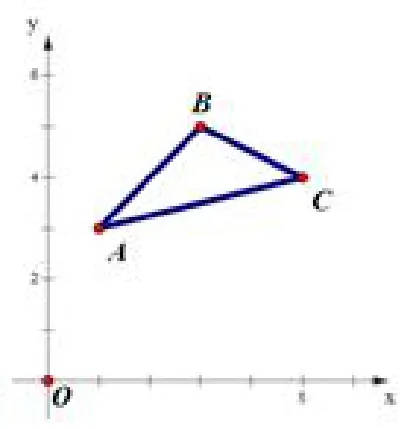
图8

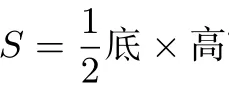
解若以AC为底,则

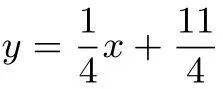
则点B(3,5)到直线AC的距离即AC边上的高为

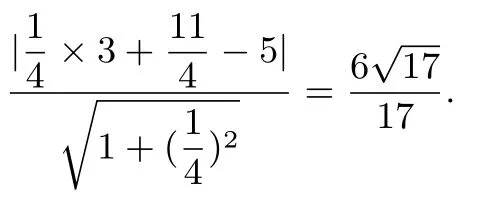
例5如图9,二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),交y轴于C(0,-2),过A,C画直线.

(1)求二次函数的解析式;

(2)点P在x轴正半轴上,且PA=PC,求OP的长;

(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.

①若M在y轴右侧,且△CHM～△AOC(点C与点A对应),求点M的坐标;

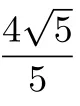
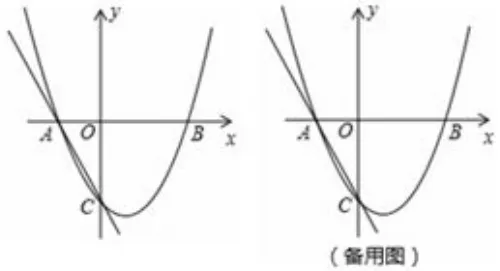
图9

解(1)抛物线的解析式为y=(x+1)(x-2),即y=x2-x-2

(2)OP=1.5

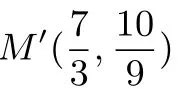
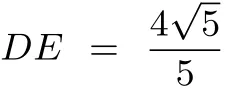
因为 ∠COA= ∠DEA=90°,∠OAC= ∠EAD,

所以△AED～△AOC,

解得AD=2,

所以D(1,0)或D(-3,0).

过点D作DM//AC,交抛物线于M,如图10(备用图)则直线DM的解析式为：y=-2x+2或y=-2x-6,

当-2x-6=x2-x-2时,即x2+x+4=0,方程无实数根,

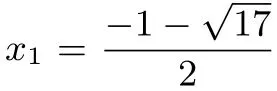
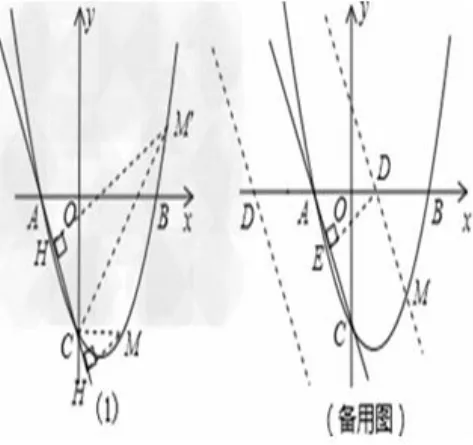
图10

分析本题是2012年宁波市中考压轴题,是一道考查二次函数、一元二次方程、勾股定理、平行线的性质、相似三角形和圆等有关知识的综合题.第(3)②题要求学生运用构造的思想,利用“平行线间的距离处处相等”找到坐标轴特殊的点,再运用函数与方程组的联系解决问题.问题的完美解决需要学生具备创造精神和质疑反思能力.而这恰恰是考生最不容易具备的,因此本小题成了众多考生失分的关键.而利用“点到直线距离公式”解答,过程将直观明了、快捷高效.

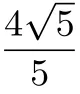
设点M(x,x2-x-2),根据“点到直线距离公式”得

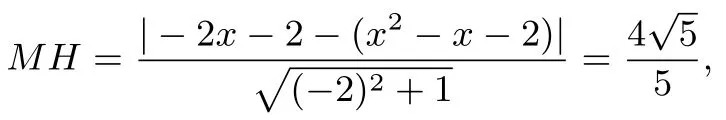
整理得|x2+x|=4,

即x2+x=4或x2+x=-4,

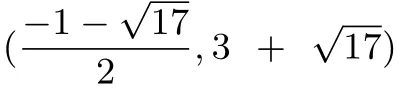
每年的中考题中都有一定数量的试题改编自课本或是课本习题.延伸性知识究其本质亦来源于教材,经过研究、拓展和提炼又以公式或结论的形式应用于数学解题中,这与现今的中考理念是一致的.延伸性知识的获得需要教师在课堂教学中不断引导学生深入浅出、举一反三地对教材内容加以推敲、延伸和变形.学生通过对延伸性知识的内化,以提升自己的解题能力.