三山岛金矿上覆断层赋存状态对巷道稳定性的影响
田莉梅 张 英 张景华(.北京科技大学土木与资源工程学院,北京 0008;2.廊坊师范学院建筑工程学院,河北 廊坊 065000;.中国石油天然气管道工程有限公司,河北 廊坊 065000)
结构面与结构体在岩体内通过不同的组合和排列而形成不同的岩体结构,不同的岩体结构其物理力学性质、力学效应以及对工程稳定性的影响有所差异。岩体内部赋存的原生节理在长期复杂地质作用下形成节理、断层、劈裂等不良结构面。井下巷道的开拓过程中会遇到各种不良地质现象,其中断层最为常见,掘进穿越断层破碎带时,围岩易出现大变形、塌方、突水等一系列地质灾害,支护难度大,加固措施不当会导致巷道失稳坍塌,危害到人员和设备安全,同时造成巨大经济损失[1-2]。
分析断层区域工程地质条件,研究断层附近围岩的强度和不同断层赋存状态下巷道的稳定性,采取针对性的巷道掘进过断层带支护方案,对巷道安全施工和稳定性保障具有重要的意义。大量工程实践和研究表明,断层倾角、断层与巷道顶板的距离、断层厚度对巷道围岩稳定性均有直接影响[3-4],本研究以三山岛金矿深部开采巷道为工程背景,采用数值模拟的方法,模拟不同赋存状态断层下巷道掘进施工过程,分析断层倾角、距离、厚度对巷道稳定性的影响,确保作业安全并制定合理的支护加固方案。
1 工程概况及模拟方案
1.1 工程概况
三山岛矿区附近赋存3个主要断层为F1、F2和F3。F1位于断裂带中偏上部,宽6~40 cm,由断层泥、糜棱岩及构造角砾岩组成;断层的走向40°,倾角35~40°,主断面延展稳定,两侧发育有1~10 m厚的碎裂岩带。F2位于在三山岛—仓上断裂的西侧(下盘)约300 m处,发育1条长900 m的分枝断裂,总体走向为50°,呈舒缓波状。构造岩带宽度为5~20 m,有绢云母化、硅化、绢英岩化热液蚀变及石英脉充填,构成构造蚀变带。F3位于三山岛—三元断裂的西北端,在矿区内长1 500 m,向北西伸向莱州湾,向南东延长到矿区之外;断层于32线与36线间通过,横贯矿区。延深大于600 m。断层走向290°~300°,倾向主要为北东,局部反倾,倾角80°以上;断层构造破碎带宽10~25 m,由充填其中的数条煌斑岩等基性脉岩及碎裂岩、角砾岩组成。
1.2 模拟方案及数值模型
为分析三山岛金矿深部开采巷道过断层掘进过程的围岩稳定性并制定加固方案,同时研究断层倾角、距离、厚度变化对巷道稳定性的影响,本研究通过数值模拟[5-7]断层倾角0°、50°、90°,水平断层距巷道顶板5、10、15 m,断层厚度10、15、20 m等工况下的巷道掘进过程,分析巷道两帮、顶板的收敛、沉降及应力分布。在巷道顶板中点、底板中点及左右两帮布置变形和应力监测点,采用分步开挖的方式模拟掘进过程,总共10步开挖,每次进尺5 m。
模型以水平垂直于巷道走向方向为X轴,平行于巷道走向方向为Y轴,铅垂方向为Z轴,巷道截面为三心拱,巷道净宽4.5 m,净高3.2 m。巷道埋深为780 m,模型在各轴上的尺寸分别为50 m、50 m和60 m,如图1所示。
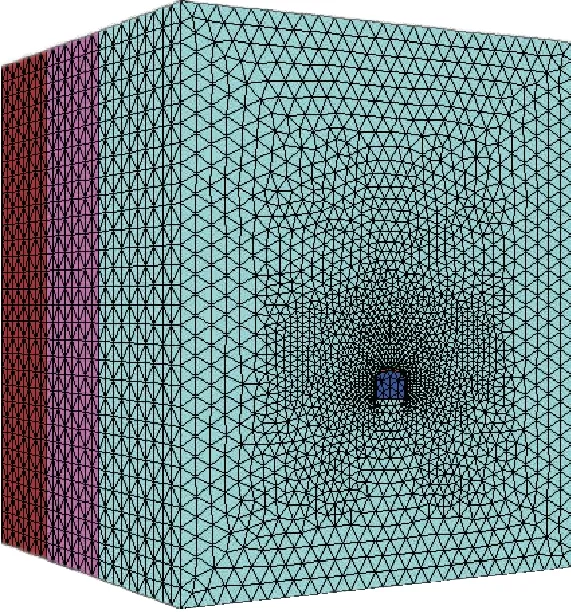
图1 数值模型Fig.1 Numerical model
依照现场地应力实测结果,对模型施加应力边界条件,模型其余边界为单向边界。最大水平主应力、最小水平主应力、垂直主应力随深部的变化规律依照下式计算:
σh,max=1.433+0.043H,
(1)
σh,min=1.304+0.024H,
(2)
σv=0.07+0.028H,
(3)
式中,σh,max、σh,min、σv分别为最大水平主应力、最小水平主应力、垂直主应力,MPa;H为深度,m。
三山岛金矿存在丰富的地下水和古海水,围岩长期处于这种高矿化度,显弱酸性的地下水中,考虑损伤效应并参考地质资料,数值计算模型选取的物理力学参数如表1所示。

表1 物理力学参数Table 1 Physical mechanics parameters
2 断层倾角对巷道围岩稳定性的影响
断层倾角是影响巷道围岩稳定性的重要因素[8-9],倾角变化对巷道的围岩变形和强度特征有直接的影响。研究断层倾角变化对巷道围岩稳定性的影响规律,可通过数值模拟实现多种倾角的工况对比。模拟方案:断层厚度15 m,距离顶板的竖直距离为10 m,选取3个倾角不同的模型进行数值模拟并对比分析无断层情况下围岩的稳定性,如图2所示,模型中监测点位移和应力监测结果如表2、表3所示。
相对于无断层的情况下,随着断层倾角的增加,巷道顶板沉降逐渐变大,两帮围岩也有明显的收敛。倾角增大过程中,各监测点的应力值也随之加大。倾角90°时巷道的各个监测点的位移值激增,此时巷道直穿断层,顶板严重破坏,说明断层破碎状况及力学性质对巷道围岩的稳定性具有控制作用。实际掘进施工过程中,尤其是巷道直穿或者斜穿断层时,必须对围岩和顶板进行安全监测,必要时采取合理的支护加固措施,确保施工作业安全。

图2 模拟方案1Fig.2 Simulation model

表2 不同倾角工况监测点位移变化Table 2 Displacement of key points in different case of dip angle mm

表3 不同倾角工况监测点应力变化Table 3 Stress of key points in different dip angle MPa
3 断层厚度对巷道围岩稳定性的影响
厚度是断层的主要特征之一,在不同的地质条件下断层的厚度有所不同,而断层厚度对巷道掘进过程中的围岩稳定性有重大影响[10]。通过模拟倾角0°,距巷道顶板10 m,厚度分别为10、15、20 m的断层下方巷道的掘进过程,研究断层厚度对巷道围岩稳定性的影响规律,如图3所示,监测点监测结果如表4、表5所示。
随断层厚度的增加,监测点的位移增加并且增长速率加快。由于断层具有高压缩性,厚度增加后,巷道开挖引起断层附近出现应力集中,导致压缩变形急剧加大,因此巷道顶部沉降和巷道底部鼓起变形均增大;断层附近应力集中导致两侧围岩体受压,在水平方向上向巷道临空面的变形增加,巷道断面收敛变形严重。模拟结果说明,随着厚度的增加,断层对巷道稳定性的影响在增大。在实际工程中,当遇到厚度较大的断层时,需要重点注意巷道顶板稳定性控制[11-12]。

图3 模拟方案2Fig.3 Simulation model 2
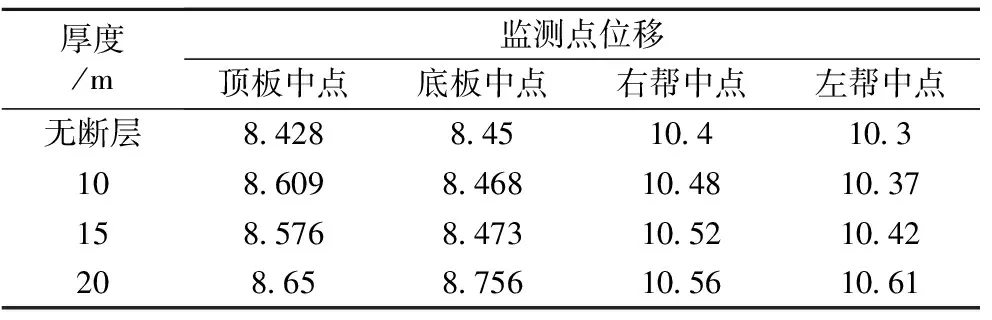
表4 不同厚度工况监测点位移变化Table 4 Displacement of key points in different thickness mm
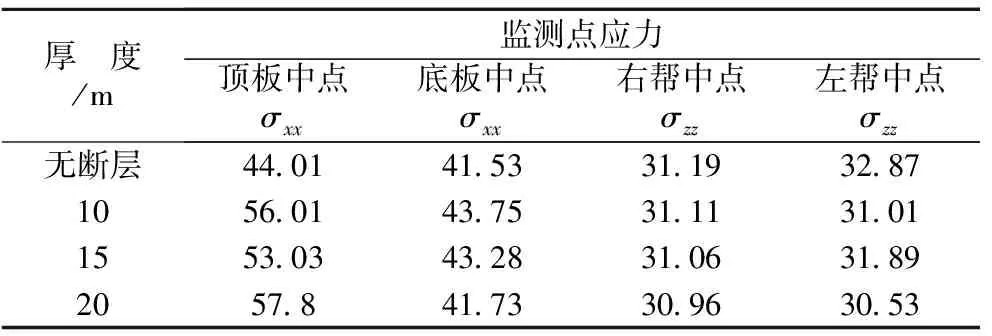
表5 不同厚度工况监测点应力变化Table 5 Stress of key points in different thickness MPa
4 断层与顶板距离对围岩稳定性的影响
巷道掘进遇断层,应当避开断层影响区域,若设计和施工条件不允许,则有必要研究上覆断层与巷道顶板不同距离时,其对巷道稳定性的影响。以倾角0°,厚度15 m断层为研究对象,模拟断层距离巷道顶板分别为5、10、15 m 这3种工况下巷道掘进围岩变形和应力的影响区域和范围,模拟方案如图4所示,监测点位移和应力见表6和表7。

图4 模拟方案3Fig.4 Simulation model 3

表6 不同距离工况监测点位移变化Table 6 Displacement of key points in different distance mm
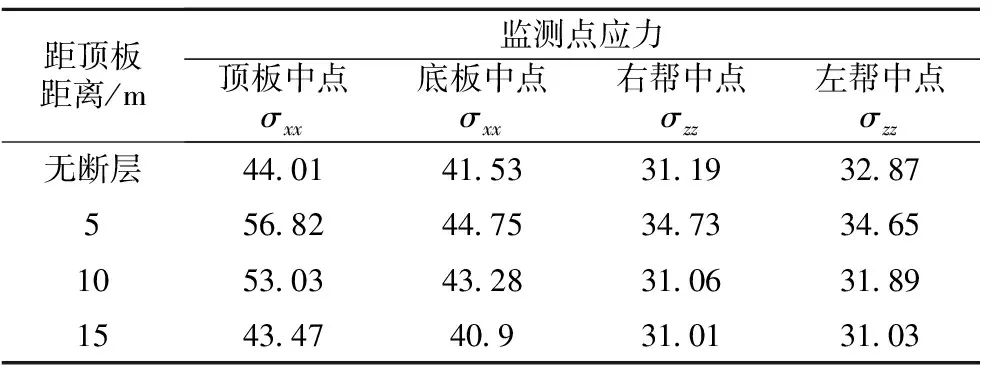
表7 不同距离工况监测点应力变化Table 7 Stress of key points in different distance MPa
结合本工程实际,断层距巷道的距离为5 m时,巷道监测点位移和应力值影响最大,随着距离的增加,影响程度逐渐减弱。当达到15 m时,断层对巷道围岩变形和稳定性基本没有影响。断层与巷道距离的变化对巷道不同点的影响程度不同,其对巷道两帮的水平位移影响较大,对巷道边帮应力的影响相对较弱,同时其对巷道顶底板中的垂直位移和应力值均产生明显的影响。
5 结 论
(1)当倾角小于90°时,随着倾角的增大,巷道顶底板位移量、边帮收敛量也随之增大;巷道顶底板和两帮的应力值也会随着倾角的增大而增加,其中巷道顶板应力变化最为明显。当倾角为90°时巷道发生破坏,此时掘进过程为巷道穿断层施工,必须进行安全监测并采取合理的支护加固措施,确保施工安全和巷道的稳定性。
(2)本工程条件下,断层在巷道顶板5 m范围内时,围岩稳定性极为不好,必须进行支护加固。5~10 m范围内时,有效控制顶板沉降即可,超出15 m时,断层对巷道掘进不产生影响。同时,断层厚度越大,其对巷道围岩的稳定性越不利,因此在开拓设计过程中需重点考虑断层赋存状态对巷道布置的影响。
[1] 宋卫东,赵增山,王 浩.断层破碎带与采准巷道围岩作用机理模拟研究[J].金属矿山,2004(2):11-13.
Song Weidong,Zhao Zengshan,Wang Hao.Simulation study on interaction mechanism between fault fracture zone and rock surrounding straight work[J].Metal Mine,2004(2):11-13.
[2] 卢邦稳,刘长武,谢 辉,等.不等长工作面覆岩活动及回采巷道采动影响变形规律[J].金属矿山,2016(1):34-38.
Lu Bangwen,Liu Changwu,Xie Hui,et al.Law of overburden strata movement and mining roadway deformation under mining influence in the unequal length of working face[J].Metal Mine,2016(1):34-38.
[3] 于 泳.过大型断层巷道设计方案优化与工程实践[J].煤炭工程,2015,47(8):44-46.
Yu Yong.Design and engineering practice on method of roadway crossing the faults[J].Coal Engineering,2015,47(8):44-46.
[4] 王文杰.高应力区巷道卸压支护技术及应用[J].金属矿山,2010(3):23-25.
Wang Wenjie.Depressurized support method and application in the development working of high stress area[J].Metal Mine,2010(3):23-25.
[5] 徐前卫,程盼盼,朱合华,等.跨断层隧道围岩渐进性破坏模型试验及数值模拟[J].岩石力学与工程学报,2016,35(3):433-445.
Xu Qianwei,Cheng Panpan Zhu Hehua et al.Experimental study and numerical simulation on progressive failure[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(3):433-445.
[6] 姜耀东,王 涛,赵毅鑫,等.采动影响下断层活化规律的数值模拟研究[J].中国矿业大学学报,2013(1):1-5.
Jiang Yaodong,Wang Tao,Zhao Yixin,et al.Numerical simulation of fault activation pattern induced by coal extraction[J].Journal of China University of Mining & Technology,2013,42(1):1-5.
[7] 勾攀峰,胡有光.断层附近回采巷道顶板岩层运动特征研究[J].采矿与安全工程学报,2006,23(3):285-288.
Gou Panfeng,Hu Youguang.Effect of faults on movement of roof rock strata in gateway[J].Journal of Mining & Safety Engineering,2006,23(3):285-288.
[8] 魏久传,高 敏,张 礼.断层倾角对工作面超前支承压力影响的数值模拟研究[J].煤炭技术,2014(6):135-137.
Wei Jiuchuan,Gao Min,Zhang Li.Influence of fault dip angle of coal face abutment pressure numerical simulation research[J].Coal Technology,2014(6):135-137.
[9] 李守国,吕进国,姜耀东,等.逆断层不同倾角对采场冲击地压的诱导分析[J].采矿与安全工程学报,2014,31(6):369-375.
Li Shouguo,lu Jinguo,Jiang Yaodong,et al.Coal bump inducing rule by dip angles of thrust fault[J].Journal of Mining & Safety Engineering,2014,31(6):869-875.
[10] 闫 帅,柏建彪,张自政,等.含水层上巷道过断层围岩破坏机制及控制[J].采矿与安全工程学报,2016,33(6):979-984.
Yan Shuai,Bai Jianbiao,Zhang Zizheng,et al.Failure mechanism and ground control of a main entry above aquifers crossing fault zone[J].Journal of Mining & Safety Engineering,2016,33(6):979-984.
[11] 戎建伟.大巷过断层带加固围岩与增强支护研究[J].煤炭工程,2013(9):38-40.
Rong Jianwei.Support and reinforcement research on roadway crossing faults[J].Coal Engineering,2013(9):38-40.
[12] 万 飞,谭忠盛,马 栋.关角隧道 F2-1 断层破碎带支护结构优化设计[J].岩石力学与工程学报,2014,33(3):531-538.
Wan Fei,Tan Zhongsheng,Ma Dong.Optimizing design of support structure for Guanjiao Tunnel in fault-rupture zone F2-1[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(3):531-538.

