江西盘古山钨矿区开采沉陷预计的GA-SVA算法
陈 慧 韩恒梅(.黄河水利职业技术学院测绘工程学院,河南 开封 475004;.平顶山工业职业技术学院资源开发学院,河南 平顶山 46700)
地下矿产资源开采活动不可避免地会给地表造成扰动,给矿区地表农田、建(构)物安全造成了较大影响。高精度监测预计矿区地表沉陷,可为地表沉陷治理及地下开采方案设计提供可靠依据[1-3]。传统矿区开采沉陷监测方法是通过在地表布置若干监测站,利用水准仪、GPS等方法进行观测[4-8],但存在耗时较长、精度不高等不足,并且难以对沉陷发展情况进行准确预计[9-12]。本研究以江西盘古山钨矿为例,采用GA算法对SVM算法进行优化,采用GA-SVM算法训练概率积分法开采沉陷预计参数,对矿区开采沉陷进行预计。
1 GA-SVA算法原理
迭代性是GA算法的一个显著特征,每次迭代过程都会求出一个随机解,以后每次迭代会产生新的解,新解的产生来源于传承和进化的遗传语言,通过多次迭代,直至结果达标为止,如此依次进行[13-15]。GA算法实现步骤为:①回到初始状态,以一定的概率产生一组符号节;②对符号节进行评估,评价标准为适度函数;③形成一组新的符号节,所使用的工具为遗传操作;④对结果进行审敛,若发散则重复操作步骤①、②。
SVM算法是一种基于结构风险最优化原则的数据分类和回归计算方法[16-17],本研究采用GA算法通过选择、交叉、变异等操作对其进行优化,主要步骤为:①确定数据的网络构成,通过对向量矩阵的权重、取值、阈值进行选择优化,获取初始数据集群,给出训练参数;②得出试验函数,根据向量机计算法则计算步骤①所选择的优化参数,进行误差矫正,误差越大说明其适应性越差,予以排除;③适应性函数寻找出适应性最大的几个数据集合,通过GA算法产生下一代数据种群;④通过GA算法的选择、交叉和变异操作生成具有代表性的数据种群;⑤基于遗传数据的种群对SVM进行训练分析,辨别数据精度是否符合精度要求,若数据无法符合精度要求,则重复步骤②~⑤,直至数据达标为止。
GA-SVM算法的相关计算因子取值见表1。
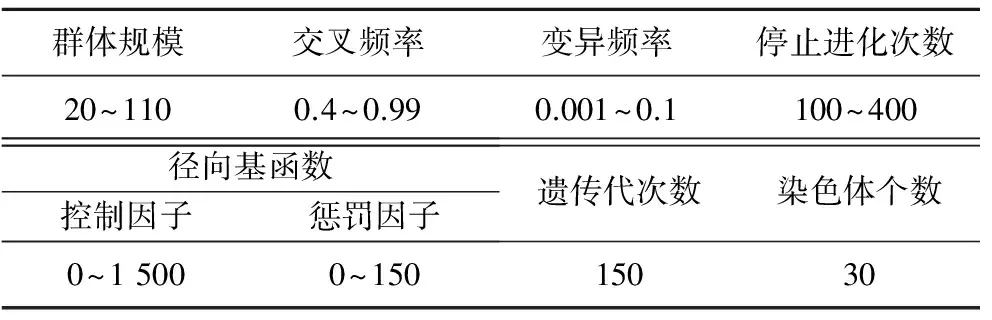
表1 GA-SVA算法相关因子取值Table 1 Relative factor values of GA-SVM algorithm
用GA-SVA算法对概率积分法开采沉陷预计参数进行了训练,结果见表2。由表2计算可知,GA-SVM算法各参数的训练值与设计值的相对误差绝对值分别为0.36%、0.71%、0.16%、0.55%,总体误差较小,表明该算法训练出概率积分法开采沉陷预计参数可靠性较强。

表2 GA-SVA算法概率积分法预计参数的训练值Table 2 Training data of the prediction parameters of probability integral method of GA-SVM algorithm
2 开采沉陷预计
研究区地处盘古山钨矿区,区内设置有2个标准站(BZ1、BZ2点)以及9个监测点位(TY1~TY9)(图1)。标准站布置于研究区西北方向,该区域地层稳定,发生地面沉陷的可能性较小。构建了3条监测线(编号依次为a、b、c),a监测路线包括TY1、TY2、TY3监测点位,b监测路线包括TY4、TY5、TY6监测点位,c监测路线包括TY7、TY8、TY9监测点位。
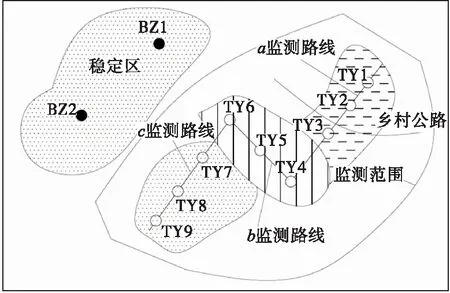
图1 研究区监测点位布置Fig.1 Distribution of the monitoring points in study area
本研究从2016年3月15日开始对研究区进行开采沉陷监测,每隔15 d监测一次,于2016年7月底结束监测,前后累计进行了10次GPS监测工作。在收集整理外业监测数据的基础上,进一步进行了数据处理,流程如图2所示。TY2、TY8点位的累计沉陷值如表3所示。
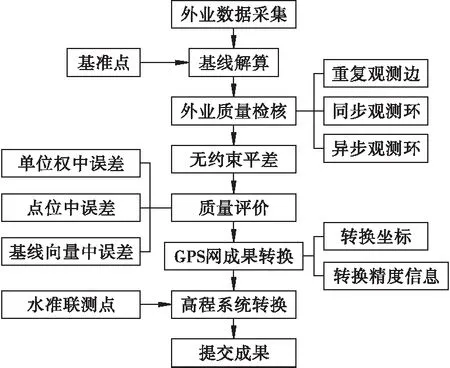
图2 研究区开采沉陷监测数据处理流程Fig.2 Processing flow of the mining subsidence monitoring data in study area
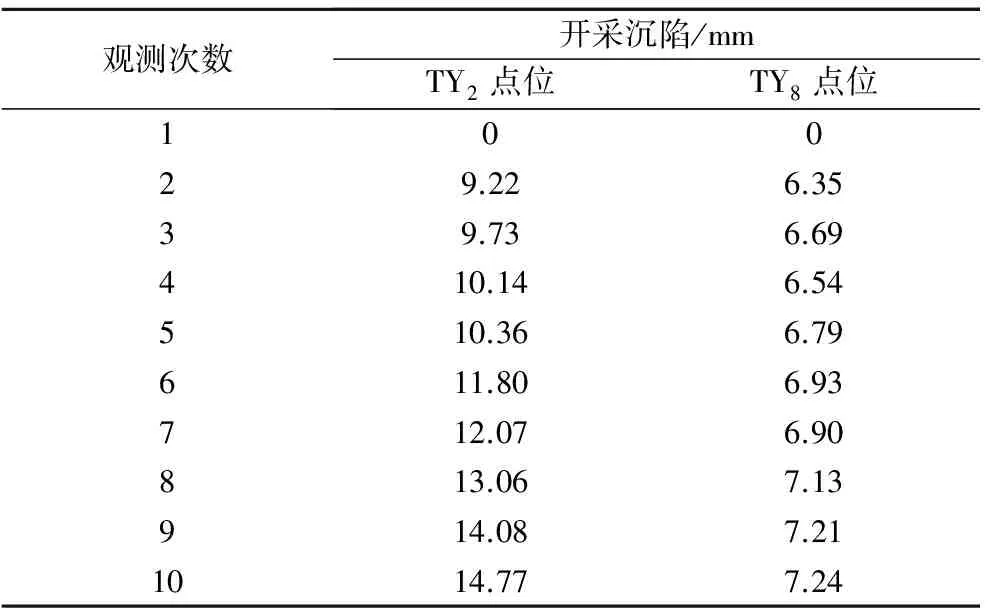
表3 TY2、TY8点位的累计开采沉陷值Table 3 Accumulated mining subsidence data of TY2 and TY8 point
结合表3中的1~7组数据对GA-SVM模型进行了训练,构建了GA-SVM开采沉陷预计模型。预计结果表明:第8次观测TY2、TY8点位的累计沉陷值分别为12.98,7.05 mm;第9次观测TY2、TY8点位的累计沉陷值分别为13.98,7.10 mm;第10次观测TY2、TY8点位的累计沉陷值分别14.71,7.42 mm,与表3中相应实测值的误差绝对值分别为0.61%、0.11%(第8次观测),0.71%、1.5%(第9次观测),0.4%、2.5%(第10次观测)(图3)。本研究中其余7个监测点位的预计值与实测值的误差小于5%,可见该模型具有较高的预计精度。
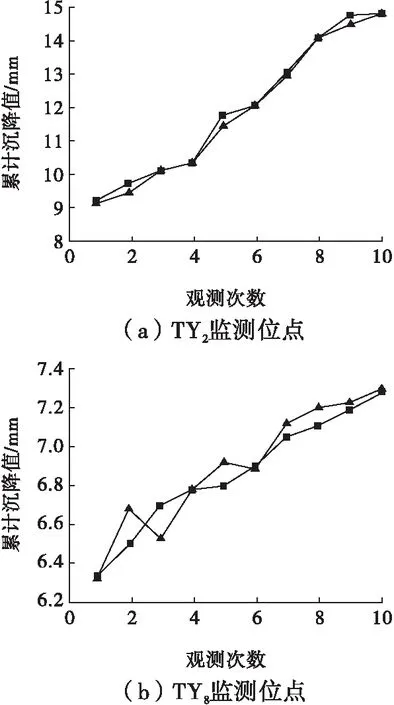
图3 沉陷预计值与实测值对比Fig.3 Comparison of the subsidence prediction data and corresponding measured data■—实测值;▲—预计值
分别采用研究区9个测点的第10期的观测值以及相应的预计值用插值方法构建了DEM,如图4所示。由图4可知,2种数据构建的DEM高度非常接近,可见,采用本研究方法预计出的沉陷值构建的DEM完全可以用于矿区下一步的沉陷分析及相关研究。
3 结 语
为有效提高江西盘古山钨矿区开采沉陷的预计精度,采用GA算法对SVM算法进行了优化,并采用GA-SVA算法对概率积分法开采沉陷预计参数进行了训练。结合矿区监测点位的GPS实测沉陷数据构建了GA-SVA沉陷预计模型,并进行了沉陷预计分析。结果表明:所提模型的预计数据与相应实测数据的误差基本小于5%,采用预计数据构建的DEM与基于相应实测数据构建的DEM较一致,表明本研究所提出的GA-SVM开采沉陷预计算法精度较高。

图4 研究区不同沉陷值构建的DEM(单位:m)Fig.4 DEM of the study area established by different subsidence data
[1] 徐孟强,查剑锋,李怀展.基于PSO算法的概率积分法预计参数反演[J].煤炭工程,2015(7):117-119.
Xu Mengqiang,Zha Jianfeng,Li Huaizhan.Parameters inversion in probability integral method by particle swarm optimization[J].Coal Engineering,215(7):117-119.
[2] 齐秀峰.基于量子神经网络拟合法的矿区地表变形监测[J].金属矿山,2016(4):154-157.
Qi Xiufeng.Surface deformation monitoring of mining area based on quantum meural metwork fitting method[J].Metal Mine,2016(4):154-157.
[3] 毛文军.基于遗传BP神经网络模型的矿区开采沉陷预计[J].金属矿山,2016(2):164-167.
Mao Wenjun.Mining subsidence prediction method based on genetic BP neural network model[J].Metal Mine,2016(2):164-167.
[4] 杨国林,李建章,李培天.基于BP神经网络的高程异常转换工程应用研究[J].矿山测量,2013(6):57-59.
Yang Guolin,Li Jianzhang,Li Peitian.Research on the conversion and engineering application of the height anomaly nased on BP neural network[J].Mine Surveying,2013(6):57-59.
[5] 吴兆福,宫 鹏,高 飞,等.基于支持向量机的GPS似大地水准面拟合[J].测绘学报,2004(4):303-306.
Wu Zhaofu,Gong Peng,Gao Fei,et al.GPS quasi geoid fitting based on support vector machine technology[J].Acta Geodaetica et Cartographica Sinica,2004(4):303-306.
[6] 王小辉,王琪洁,丁元兰,等.基于二次曲面和BP神经网络组合模型的GPS高程异常拟合[J].大地测量与地球动力学, 2012(6):103-105.
Wang Xiaohui,Wang Qijie,Ding Yuanlan,et al.Combined model in height anomaly fitting[J].Journal of Geodesy and Geodynamics,2012(6):103-105.
[7] 胡伍生,华锡生,鲍兴南.转换GPS高程的神经元网络方法[J].河海大学学报:自然科学版,2001(6):87-89.
Hu Wusheng,Hua Xisheng,Bao Xingnan.Neural network method for GPS height transformation[J].Journal of Hehai University:Natural Sciences Edition,2001(6):87-89.
[8] 杨建图,姜衍祥,周 俊,等.GPS测量地面沉降的可靠性及精度分析[J].大地测量与地球动力学,2006(1):70-75.
Yang Jiantu,Jiang Yanxiang,Zhou Jun,et al.Analysis on reliability and accuracy of subsidence measurement with GPS technique[J].Journal of Geodesy and Geodynamics,2006(1):70-75.
[9] 沈玉娜,万广欣.GPS在区域地面沉降监测中的应用[J].矿山测量,2016(4):16-18.
Shen Yuna,Wan Guangxin.Application of GPS in Regional Ground Subsidence Monitoring[J].Mine Surveying,2016(4):16-18.
[10] 刘国林,张连蓬,成 枢,等.合成孔径雷达干涉测量与全球定位系统数据融合监测矿区地表沉降的可行性分析[J].测绘通报,2005(11):13-16.
Liu Guolin,Zhang Lianpeng,Cheng Shu,et al.Feasibility analysis of monitoring mining surface substance using InSAR/GPS data fusion[J].Bulletin of Surveying and Mapping,2005(11):13-16.
[11] 侯林山,王金龙,朱三妹,等.利用差分GPS进行地面沉降监测的研究[J].岩土力学,2006(5):811-815.
Hou Linshan,Wang Jinlong,Zhu Sanmei,et al.Study of difference GPS to monitor Land Subsidence[J].Rock and Soil Mechanics.2006(5):811-815.
[12] 高永芹.矿区开采沉降监测中GPS的应用研究[J].煤炭技术,2013(4):124-126.
Gao Yongqin.Application of GPS in mining subsidence monitoring[J].Coal Technology,2013(4):124-126.
[13] 杨泽发,易辉伟,朱建军,等.基于InSAR时序形变的矿区全盆地沉降时空演化规律分析[J].中国有色金属学报,2016(7):1515-1522.
Yang Zefa,Yi Huiwei,Zhu Jianjun,et al.Spato-temporal evolution law analysis of whole mining subsidence basin based on InSAR-derived time series deformation[J].The Chinese Journal of Nonferrous Metals,2016(7):1515-1522.
[14] 王 磊,郭广礼,王明柱,等.山区地表移动预计修正模型及其参数求取方法[J].煤炭学报,2014(7):1070-1076.
Wang Lei,Guo Guangli,Wang Mingzhu,et al.New method of updating design for model and its parameter to prediction surface movement in mountainous mining[J].Journal of China Coal Society,2014(7):1070-1076.
[15] 孙 冉.概率积分法参数求取和模型修正方法研究及程序实现[D].淮南:安徽理工大学,2017.
Sun Ran.Research on the Method of Parameter Estimation and Model Updating Based on Probability Integral Method and Program Realization[D].Huainan:Anhui University of Science and Technology,2017.
[16] 张 豪,罗亦泳,张立亭.基于遗传支持向量机的城市扩张非线性组合模型[J].地理学报,2010(6):656-664.
Zhang Hao,Luo Yiyong,Zhang Liting.A nonlinear polynomial model for urban expansion incorporating genetic algorithm and support vector machines[J].Acta Geographica Sinica,2010(6):656-664.
[17] 拓万兵,姜 伟,吴凤民.基于支持向量机的开采沉陷预计参数选取研究[J].中国矿业,2015(2):114-116.
Tuo Wanbing,Jiang Wei,Wu Fengmin.Study on the selection of prediciton parameters on mining subsidence based on support vector machine[J].China Mining Magazine,2015(2):114-116.

