露天矿采矿作业计划的二元整数规划数学模型

黄 敏 李学华 贾 民(.广州南洋理工职业学院，广东 广州 50980；2.中国矿业大学矿业工程学院，江苏 徐州 226;3.深部煤炭资源开采教育部重点实验室，江苏 徐州 226;.兖州煤业股份有限公司济宁二号煤矿，山东 济宁 272000)

对于露天矿年度作业计划来说，边界品位优化问题是一个重要的研究挑战。在矿产资源行业，通过每个时期的最优边界品位计算可以获得相当大的经济效益，从而最大化采矿项目的净现值(net present value，NPV)[1]。因此，露天采矿作业中与矿块开采顺序相关的，最复杂的问题之一就是边界品位选择。

边界品位直接影响到项目寿命期内采矿作业的经济可行性。为了得到给定项目的更高整体净现值，需要选择适当的边界品位策略。在采矿顺序的初始阶段，更高的边界品位会导致每吨矿石的平均等级更高，因此，可以通过矿床的品位分布研究来实现更高的平均品位[2]。采矿项目的成功与否直接取决于边界品位的选择。因此，在矿山开采中，边界品位优化是必不可少的[3]。

文献[4]提出了一种基于遗传算法和拓扑排序相结合的作业计划优化方法，但不能保证最终解决方案的质量。文献[5]使用几种策略相结合来减少计算时间。Nasab等人在文献[5]基础上，提出了一种聚集并应用了拉格朗日松弛原理[6]。到目前为止，这些模型不能满足每一阶段内品位混合的质量要求。文献[7]对不同的作业技术和建模问题开展了广泛的调查。任何给定时期的动态边界品位可以视为这一时期关于矿石供应和铣削需求的一个函数。研究人员不断尝试通过各种计算机处理方法来实现露天矿开采顺序优化。但是由于具有许多相关的变量，现有方法都没有得到广泛的认可。

众所周知，忽略采矿顺序中这些变化对最优边界品位的影响，将导致不切实际的矿山设计和分析。因此，本研究提出了一种新的二元整数规划模型来求解开采顺序问题。介绍了边界品位对开采顺序的影响。给出了以矿块经济损失评估和矿体品位概率分布为基础的公式。通过物理约束将一个矿块的经济损失评估与概率集成在一个二元整数规划模型[8]中。该模型的最终目标是设定最佳开采顺序，同时优化矿山各时期的边界品位。

1 露天矿边界品位优化的必要性

边界品位分析，一般来说可以解决以下问题：

(1)矿床中的哪些块段值得开采和加工，如果不是，则应该被认为是废石。

(2)一旦开采，该如何加工。

实际上，边界品位计算的目的是为了发送从矿山中提取的矿物，图1显示了基于边界品位的决策准则。

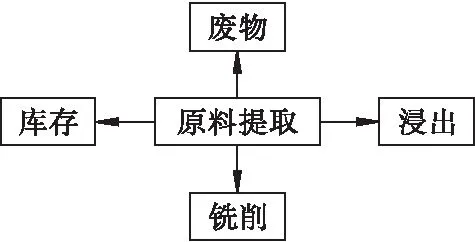
图1 基于边界品位的决策准则Fig.1 Decision criteria based on boundary grade

一个静态边界品位不具备在不同情况下实现利润最大化所需的灵活性[4]。边界品位优化是一个相互作用的过程，包括金属价格、采矿成本、加工成本、加工能力、采矿作业能力、开采顺序、矿床品位分布以及由此产生的现金流。矿块的加工决策在采掘顺序变更中起主要作用。在矿山开采过程中，由于矿山净现值递减效应的变化，使得矿山开采阶段的开采效果会发生很大的变化。因此，在采矿顺序中应同时考虑边界品位的优化[4]。边界品位优化是采矿作业中最重要的课题之一：

(1)边界品位优化用于加工类型(铣削/矿物堆浸/废石堆浸/废弃)的决策问题，以确定哪种决策决定了最大的经济利润。

(2)边界品位优化可改善矿山开采顺序。

2 考虑动态边界品位的开采顺序公式

2.1 定 义

在开采顺序问题中，每个阶段内每个块的开采取决于边界品位的定义。边界品位决定块分类。对一个块的错误分类会导致错误的矿块经济价值计算结果。在这方面，文献[9]定义了一种“经济损失”函数，用来区分矿石和废石。与每种加工类型d(d=1，2，……D，从最低等级到最高等级排序)相关的实际经济损失可以用以下等式计算：

(1)

从式(1)可以看出，如果块ijk正确选择加工类型，那么经济损失为零。在实践中，矿块是未知的，它将用累积分布函数来表示。一个较实际的方法是使用条件模拟技术，它能够实现一定数量同等概率的块级。考虑到这一点，根据每一种加工处理的概率分布和平均品位，对每一个选择d的预期经济损失(expected economic loss，EEL)进行计算，其具体描述如下所示：

(2)

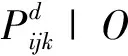
矿块ijk的最优加工类型是具有最小EEL的d，如：

(3)

2.2 作为整数问题的公式

根据上述定义和假设，建立了整数决策变量形式的开采顺序数学规划模型[11]，并在此基础上确定了特定块的开采时期及其目的地。事实上，该模型可以同时优化矿块开采顺序和边界品位。如前所述，模型的目标函数可以用数学形式表示如下：

(4)

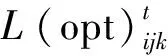
∀t，

(5)

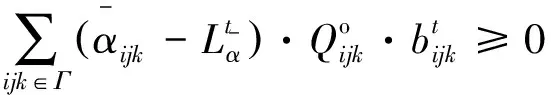
(6)

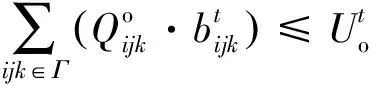
(7)

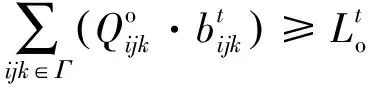
(8)

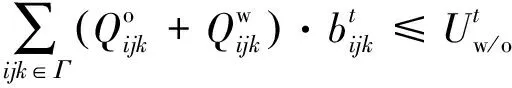
(9)

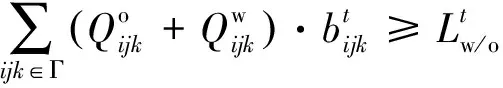
(10)

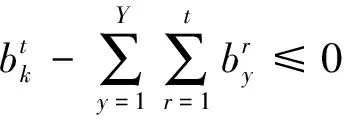
(11)

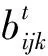
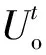
约束条件(5)、(6)将送去铣削物料的平均品位限制在某一值上。约束(7)强制只在一个时期内删除矿块。约束(8)、(9)确保铣削能力保持不变。这些上限和下限是保证矿石顺利供应所必需的。约束(10)、(11)与每个时期实际可用的设备容量相关。约束(12)是各时期各矿块基于Y的边坡限制。

该模型提供了一种评估可选策略的工具，可作为长期生产调度可行性研究的一部分。因此，由此产生的边界品位有助于风险量化决策过程。

提出的数学规划模型方法步骤如下。

(1)该模型的基础条件为一个三维块模型，并完成了露天最终境界圈定。

(2)在每个开采时期开始时，包括采矿和加工阶段能力、采矿成本和加工类型成本以及当前金属价格等参数已知。

(3)使用序贯高斯模拟得到了若干概率相同的矿块模型的实现。

(4)为每个加工类型提供每个块的经济损失矩阵，并随后计算每个可选d的EEL。

(5)构建混合整数规划模型，以便根据指定的标准对每个时期内的矿块进行最优选择。

3 应用实例

在本节中，我们在真实的采矿区实现和测试了提出的模型，以确保矿块开采顺序的最优性和边界品位优化。一个金矿把它的矿化产品送到4个目的地：废料堆、废石堆浸、矿物堆浸或铣削。这4个类型的特性列于表1中(黄金价格以10 $/g为例)。首先，利用序贯高斯模拟方法，产生了矿体金品位的一百个等概率实现。给定块的模拟结果如表2所示。

表1 金矿床各矿化块分类特征Table 1 Classification characteristics of mineralized blocks in gold deposits

表2 金矿床某给定块的模拟结果Table 2 Simulation results of a given block of gold deposits

表3 矿块分类的经济损失结果Table 3 Economic loss results of ore block classification

例如，假设块ijk的一个正确采矿目的地是废石堆浸(d=3)，但却被错误地送到废料堆(d′=2)，那么由于这个造成的经济损失评估可以从式(1)计算得到，如：

-[(10-0.5)·1.5·0.45-3.5]

=2.81.

(12)

表3显示了d和d′其他值的经济损失结果。如果块ijk选择的分类是d=2，那么由错误分类导致的预期经济损失可以从式(2)得到，如：

+1.362×0.2+14.375×0.17

=2.81.

(13)

根据表3，最佳预期经济损失是1.69，因此，这个块的最佳目的地是d=3，这意味着最好将此块发送到矿物堆浸。

在开采顺序问题中，各时期中每块的开采都取决于该时期的经济价值。另一方面，由于时间和价格的变化，块的经济价值随时间而变化，因此，一个时期的最优矿块分类可能与其他时期的最优矿块分类不同。相应地，时期t块ijk的损失函数可由式(4)计算得到。由于经营需求，最小化的目标函数受到式(5)～式(12)的约束。

由于优化的迭代步骤既枯燥又耗时，因此开发了一个Excel电子表格，以便于计算。输入参数包括：每个块的计数器特征，每个块的吨位、矿石品位和含量，每个块的预期经济损失。考虑模型中决策变量和与矿块类型相关的可用约束。我们的目标是为5 a的矿山开采作业，生成一个维持8%贴现率的时间表。

按照上一节中给出的模型步骤，并根据生产率和净现值组合，可以得到最优的边界品位。表4显示了黄金矿山的最优边界品位、相应的生产率和NPV。

表4 黄金矿山的最优边界品位、相应的生产率和NPVTable 4 Optimum border grade，corresponding productivity and NPV of gold mine

如表4所示，在1 a期间，堆浸矿石处理将金属含量保持在1.96%到2.36%。这就说明1.96%以下的材料被视为废物并运到垃圾堆中。尽管如此，它仍产生一个最优净现值。

4 结 论

本研究提出了一种基于露天矿二进制整数规划的数学模型，能够在考虑动态边界品位优化的情况下优化开采顺序，实现净现值最大化。该模型能够产生一个切实可行的加工类型计划表，在满足系统限制的情况下最大限度地减少预期经济损失。虽然该模型以经济损失为目标函数没有直接最大化NPV，但是它提供了一个切实可行的净现值(在同时考虑边界品位优化和开采顺序优化情况下，该净现值是最优的)。该模型克服了传统方法的局限性，减少了需要的变量数量，能够在短时间内处理可用变量和约束。案例研究的结果表明，该模型具有较好的灵活性，可以有效用于各种备选方案的评估，并确保最佳的资源利用率以及准确的大型矿业投资决策。

[1] 蒋成荣,彭平安,王李管.沙溪铜矿开采边界品位动态优化方法[J].金属矿山,2016(9):73-77.

Jiang Chengrong，Peng Ping′an，Wang Liguan.Dynamic optimization method of mining marginal grade in Shaxi Copper Mine [J].Metal Mine，2016(9):73-77.

[2] 蒋成竹,王庆飞,万 丽,等.云南三江地区典型金矿床吨位-边界品位曲线特征[J].岩石学报,2012，28(5):1551-1560.

Jiang Chengzhu,Wang Qingfei,Wan Li,et al.Tonnage-cutoff grade curves for the typical gold deposits in the Sanjiang area[J].Acta Petrologica Sinica,2012,28(5):1551-1560.

[3] 彭平安.地下多金属矿床边界品位优化及经济开采研究[D].长沙：中南大学,2014.

Peng Ping′an.Study on Boundary Grade Optimization and Economic Exploitation of Underground Polymetallic Deposits[D].Changsha:Central South University,2014.

[4] Wang Y,Sun Y,Tong W.Optimization of wireless sensor networks in open-pit mine slope detection based on genetic algorithms[J].Computer Measurement & Control,2011,19(2):483-486.

[5] Boland N,Dumitrescu I,Froyland G,et al.LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity[J].Computers & Operations Research,2009，36(4):1064-1089.

[6] Nasab H A,Awuah-Offei K,Eivazy H.Large-scale open pit production scheduling using mixed integer linear programming[J].International Journal of Mining & Mineral Engineering,2010，2(3):338-359.

[7] Newman A M,Rubio E,Caro R,et al.A review of operations research in mine planning[J].Interfaces,2010,40(3):222-245.

[8] 罗宗杰.基于混合整数二元规划的机组启动次序策略研究[J].电力系统保护与控制,2012，40(11):112-116.

Luo Zongjie.Study on startup order strategy of unit based on mixed integer two element programming[J].Power System Protection and Control,2012,40(11):112-116.

[9] Abascal J.Users with disabilities:Maximum control with minimum effort[C]∥International Conference on Articulated Motion and Deformable Objects.Berlin：Springer-Verlag,2008:449-456.