低真空环境下四极杆质量分析器灵敏度仿真研究

姜佩贺，周志权,，陈焕文，赵占锋

(1.哈尔滨工业大学，电子与信息工程学院，黑龙江 哈尔滨 150001；2.哈尔滨工业大学(威海)，信息与电气工程学院，山东 威海 264209；3.东华理工大学，江西省质谱科学与仪器重点实验室，江西 南昌 330013)

质谱仪的小型化和便携化一般可以通过两种方式实现：一种方式是减小离子阱的尺寸，进而降低质量分析所需要的扫描电压，简化控制电路，从而减小质谱仪的体积，这是目前小型质谱仪的常用实现方案[1-3]。但是由于真空系统的限制，难以将其尺寸进一步缩小；另一种方式是简化真空系统，降低质量分析所需要的真空度。如在一级真空条件下进行质量分析，不仅可以省掉体积庞大的分子泵，降低系统的功耗、成本，提高系统鲁棒性，而且可以简化离子传输系统[4]，使质谱仪的小型化和便携化实现质的飞跃。低真空环境下的质量分析将引领小型质谱仪的下一次革新[5]。

四极杆是质量分析器的一种，在质谱仪中具有广泛的应用。将具有一定初速度的离子入射到四极杆，在四极场的作用下，离子的运动分为稳定和不稳定两种状态，理论上，稳定运动的离子在四极杆中进行周期性的振荡运动，可以穿过四极杆到达位于最末端的检测器。但在实际工作中，由于环境真空度、四极杆装配、边缘场效应等因素的影响，并非所有理论上稳定运动的离子都能够遵循既有轨迹进行稳定运动。

当质量分析环境压强提高，质谱仪的性能主要在两个方面发生变化：一是质量分辨率，二是灵敏度。质量分辨率是指质谱仪区分两种质量相近离子的能力，当压强提高时，离子与背景气体的碰撞频率增加，离子运动轨迹发生变化，质量分辨率降低，谱峰延展。Xu等[6]通过理论计算，得到了半峰宽(FWHM)与压强的关系，并指出在离子阱中，当以空气作为背景气体，压强为33.33 Pa时，半峰宽为9.5 u。Song等[7]利用实验对Xu等的计算进行了验证，同时指出当压强为0.55 Pa时，半峰宽为0.98 u。仪器的灵敏度可以用离子通过率衡量，离子通过率是指在四极杆中到达检测器的离子数量与稳定运动离子数量的比值。在低真空环境下进行质量分析，灵敏度会下降，但通过改变离子操作模式，可以减小真空度对灵敏度的影响。

针对低真空下的质量分析机理，Whetten[8]指出有阻力时粒子的运动仍可以用Mathieu方程进行描述，并给出了粒子的运动模型；Hasegawa等[9]利用数学分析方法分析了有阻力情况下稳定区的变化；Whitten等[10]讨论了第一稳定区的变化，更侧重于采用数学方法对离子运动频率进行分析。总结发现，针对低真空环境下的质量分析，已有研究均停留在讨论压强变化对质量分析机理的影响上，没有真正给出适用于低真空的切实可行的离子操作模式，且已有研究均将真空度的降低(即压强提高)视为离子运动的阻力，通过添加阻尼项讨论离子的运动趋势，进而得到稳定区的变化，这种建模方法所使用的模型称为阻力模型，它反映了离子进行大量碰撞后的平均运动趋势，但不能准确反映低真空下分立离子的运动情况，且无法评估假设的阻尼系数与压强之间的关系。在低真空质量分析中引入碰撞理论，可以更准确地描述分立离子的运动情况，进而得到可应用于低真空环境的离子操作模式。

为了深入研究质谱仪在低真空下的离子操作模式，本工作拟针对四极杆质量分析器，扩展阻力模型，利用Langevin碰撞理论，在有限元数值分析软件COMSOL Multiphysics中搭建仿真平台，讨论低真空环境下，背景气体压强、离子质荷比、背景气体质量、离子初速度、四极杆半径以及温度等因素对离子通过率即质谱仪灵敏度的影响，探讨在低真空环境下通过改变操作模式提高灵敏度的方法，希望为低真空度质谱仪的设计提供技术支持。

1 仿真程序设计

目前，针对离子运动轨迹的仿真主要有ITSIM[11]、ISIS[12]、SIMION[13]等软件，它们都是基于有限差分法，虽然方法相对直观，计算速度快，但难以处理复杂的不规则求解域。COMSOL Multiphysics是一款以有限元分析为基础的大型通用CAE软件，有限元分析更易实现对偏微分方程的离散分析，适合处理复杂区域并保证计算精度[14]。COMSOL Multiphysics拥有大量预定义的应用模块，本研究选用静电模块(es)、电流模块(ec)和带电粒子追踪模块(cpt)实现仿真程序的设计，其主要步骤示于图1。

图1 仿真程序设计流程Fig.1 Flow chart of the simulation program

1.1 四极杆与四极电场模型的创建

COMSOL中几何模型的创建方式有两种：一种是利用COMSOL自带的几何工具创建模型；另一种是通过CAD等软件创建几何模型后，导入到COMSOL中。由于四极杆模型相对简单，因此选择前者来完成创建。

定义极杆的半径为re，极杆长度为L，每个极杆距离中心的距离为r0=re/1.148，研究表明，该比例可以得到更纯净的四极场[15]。同时，将半径为4re，长度为L的圆柱形区域定义为求解区域。当re=7.5 mm，L=152 mm时，建立的四极杆几何模型结构示于图2。

注：a.x-y平面视图；b.三维视图图2 四极杆几何结构模型Fig.2 Geometric structure model of quadrupole

根据四极杆理论[16]，上下两个电极施加电势+φ0，左右两个电极施加电势-φ0，其中，

式中，a和q为Mathieu方程的参数，ω为交变电压的扫描频率，mi为离子的质量，e为单位电荷的电量。这样就在四极杆中形成了可以用于离子选择的四极场。此外，在实际的四极杆质量分析器中，离子入口和出口之间会有一定的电压差，设定入口端盖电势为U0，出口端盖电势为0。

1.2 离子的释放与碰撞

应用COMSOL中的带电粒子追踪模块(cpt)实现离子释放与碰撞的模拟，在四极杆入口端盖的中心处划定半径为rsrc=0.5 mm的圆形区域为离子释放区域。释放的离子质量为mi，电荷数为1，离子在交变电压的第一个扫描周期内释放10次，每次释放50个，即在一次仿真中共释放了500个离子，离子初速度沿x轴方向，大小为vx0。在四极杆中，离子的初速度是通过加速电压UA对离子进行加速得到的，它们之间的关系为

(1)

此外，设定“壁条件”为“冻结”，即离子打在四极杆表面不发生反射，冻结在壁表面。离子在电场的作用下运动，并不断与背景气体发生碰撞。假定背景气体分子静止，其质量为mg，密度数为Nd，Nd与压强p的关系为：

(2)

其中，NA为阿佛加德罗常数，R为气体常数，T为绝对温度。

当真空度降低即压强提高时，真空腔中背景气体分子数增多，带电离子与背景气体分子之间的碰撞概率大大提高。对于Langevin 碰撞模型[17]，离子与惰性气体分子相互靠近时，在带电离子的作用下，气体分子内部产生一个诱导偶极，离子与产生的诱导偶极发生库仑作用。当靠近到一定距离时，两者发生能量交换，完成一次碰撞，其碰撞截面积为：

(3)

其中，q为离子所带电荷量，ε0为真空中的介电常数，v为离子和背景气体分子的相对速度，αe为气体分子极化率，μ为约化质量(reduced mass)。

对于Langevin 模型，离子与背景气体的碰撞频率为：

P=Ndvσ

(4)

由式(2)、(3)、(4)得：

(5)

其中，k为玻尔兹曼常数。

1.3 网格的剖分

COMSOL是以有限元分析为基础的，因此需要进行网格剖分。网格剖分的精细程度决定解的准确性，但剖分得越精细所需要的计算时间越长。由于四极杆模型为圆柱形模型，在几何结构上沿z方向是相同的，因此通过先在x-y平面进行三角形剖分，而后在z方向进行扫掠的方式完成网格剖分。

在x-y平面上采用“自由剖分三角形网络”，单元尺寸为“超细化”，设定曲率因子为0.15。扫掠分布属性采用“预定义分布类型”，单元数为35，单元细长比为15，分布方式为等差数列，剖分结果示于图3。在x-y平面上四极杆边缘处的网格较密，在z方向上，网格呈等差数列的方式逐渐稀疏，这样的剖分方式很好地平衡了计算速度与解的精度之间的关系。

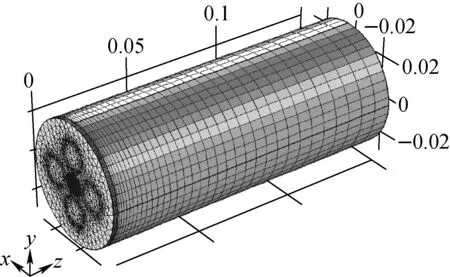
图3 网格剖分结果Fig.3 Result of mesh generation

1.4 仿真结果

由于采用了静电、电流和带电离子追踪模块，因此，研究分为3步，即通过“稳态”求解静电场，通过“频域”求解交变电场，通过“瞬态”求解带电粒子追踪。

设定仿真条件：极杆半径re=7.5 mm，极杆长度L=152 mm，Mathieu方程参数a=0.2、q=0.7，扫描频率ω=0.768 MHz，背景气体压强p=3 Pa，背景气体质量mg=4 u，离子质量mi=40 u，离子加速电压UA=2 V，入口处端盖电极电压U0=5 V，得到的仿真结果示于图4、图5。

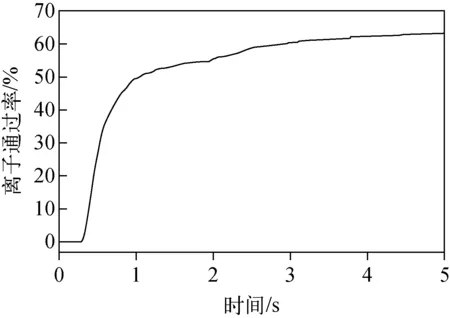
图4 不同时刻的离子通过率Fig.4 Ions transmission probability at different time

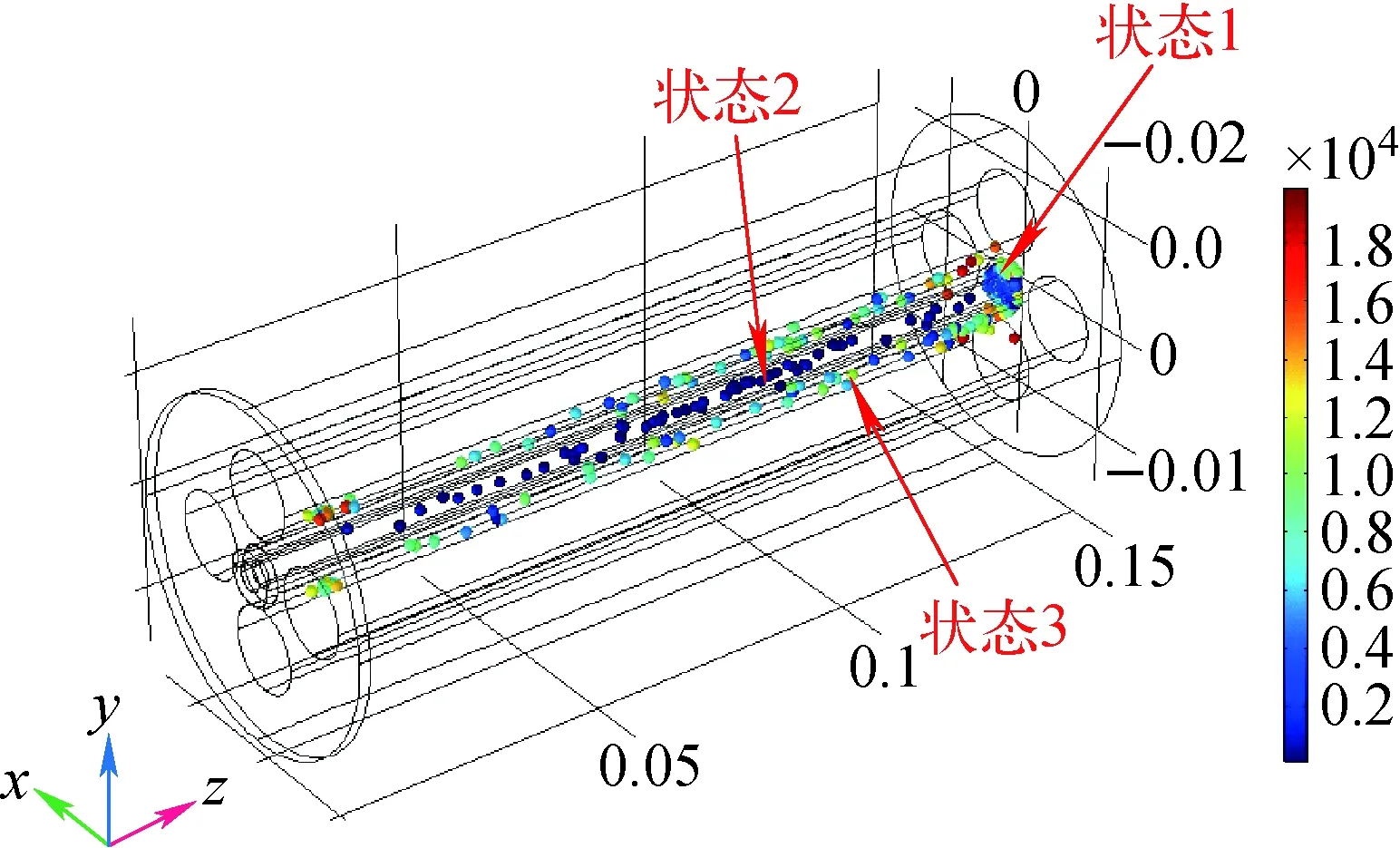
注：p=3 Pa，t=5×10-4 s图5 离子的运动状态Fig.5 Ions motion state

图4给出了离子通过率随时间的变化，离子从0.3×10-4s开始到达检测器，而后逐渐增多，最终通过率保持在63%左右。图5给出了离子在5×10-4s时刻的位置和能量信息，离子的颜色表征了离子在该时刻的能量。由四极杆理论[16]可知，当前的(a，q)值位于稳定区内部，理论上所有离子的运动都是稳定的，都可以穿过四极杆到达位于最末端的检测器。但由于真空度降低，离子与背景气体发生碰撞，离子的运动分成了3种情况：一是离子穿过四极杆，到达检测器，如图5中的状态1所示；二是由于碰撞，离子轴向动能逐渐降低，虽存在轴向静电场的作用，但离子运动极为缓慢，在一定时间内无法到达检测器，如图5中的状态2所示；三是由于碰撞，离子运动偏离原轨道，打在极杆上，无法到达检测器，如图5中的状态3所示。

传统的阻力模型中，认为离子受到的阻力与速度成正比，离子的运动是一个振幅越来越小的阻尼运动，只能得到如上前两种运动状态[6-8]。在引入Langevin碰撞理论后，得到了如上3种离子运动状态，与实际情况更为相符。可见，在低真空质量分析中引入Langevin碰撞理论，可以更准确地反映离子的运动状态。

2 结果与讨论

2.1 真空度对灵敏度的影响

设定仿真条件：极杆半径re=7.5 mm，极杆长度L=152 mm，马修方程参数a=0.2、q=0.7，扫描频率ω=0.768 MHz，离子质量mi=40 u，背景气体质量mg=4 u，离子加速电压UA=2 V，入口处端盖电极电压U0=5 V，环境温度20 ℃。改变背景气体压强，通过仿真计算得到气体压强与离子通过率之间的关系，结果示于图6。可知，在真空条件下，离子通过率为100%，随着压强的升高，离子通过率逐渐降低，当压强升高到8 Pa时，离子通过率减小到0。

图6 背景气体压强与离子通过率的关系Fig.6 Relationship between background gas pressure and ions transmission probability

由式(5)可知，碰撞频率与压强成正比，当背景气体压强升高，真空腔内的背景气体分子数量增多，与离子的碰撞频率增加，导致通过率降低，即灵敏度降低。提高压强，导致质谱仪灵敏度的降低，如何在高压强下，最大限度的减小灵敏度的降低，是实现低真空质量分析的关键。

2.2 离子和背景气体质量对灵敏度的影响

设定背景气体压强p=3 Pa，其他条件不变，改变待分析离子质量，得到了不同质量离子的通过率，结果示于图7。当离子质量小于100 u时，通过率随离子质量的增加而增加；当离子质量大于100 u时，通过率保持在98%附近。

图7 待分析的离子质量与离子通过率的关系Fig.7 Relationship between ion mass and transmission probability

不同质量的离子在相同的电场条件下入射到四极杆，具有相同的动能，而质量大的离子具有更高的动量，碰撞对其构成的影响较小。因此，离子质量越大，其通过率越高。当离子质量远大于背景气体质量时，碰撞对其影响微乎其微，因此通过率几乎保持不变。由此可知，大质量的离子在低真空下可以获得更高的灵敏度。

背景气体分子质量的变化也会对离子通过率造成影响，针对mi=100 u的离子，改变背景气体分子质量mg，得到背景气体质量与离子通过率的关系，结果示于图8。随着背景气体分子质量的增加，离子通过率逐渐降低，当mg由4 u增加到50 u时，离子通过率由97%减小到8%。

背景气体质量越小，具有的动量越低，对穿越四极杆的离子影响越小，离子通过率越高。因此，利用小质量的气体(如氦气)作为背景气体，更有利于得到较高的灵敏度。

2.3 加速电压对灵敏度的影响

在离子进入四极杆之前，需要利用加速电压对其进行加速，使离子在沿轴方向上具有一定的初速度。设定其他条件不变，背景气体质量mg=4 u，背景气体压强p=3 Pa，针对质量为40 u的离子，在不同加速电压下的通过率示于图9。增大加速电压，离子通过率显著提高，当加速电压由1 V增加到10 V时，离子通过率由54%增加到95%。这是因为加速电压升高，离子初动能提高，动量增大，碰撞能力增强，通过率提高。但过高的速度会使离子碰撞为碎片，无法完成质量分析。因此，在一定范围内增大加速电压，有助于提高仪器的灵敏度。

图8 背景气体分子质量与离子通过率的关系Fig.8 Relationship between background gas mass and transmission probability

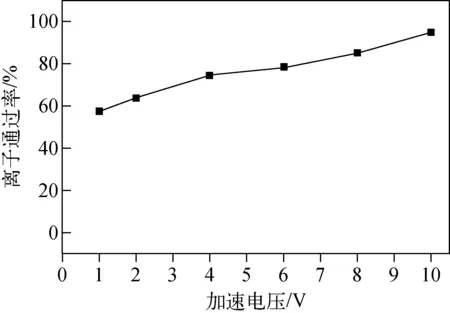
图9 加速电压与离子通过率的关系Fig.9 Relationship between accelerating voltage and transmission probability

2.4 四极杆半径对灵敏度的影响

四极杆半径的大小也是影响离子通过率的一个重要因素。改变四极杆半径re，同时保持每个极杆与四极杆中心的距离为r0=re/1.148，不同re下的离子通过率示于图10。可见，re越大，离子通过率越高，当极杆半径由4 mm增大到20 mm时，离子通过率由28.5%增大到85%。因此，较大的四极杆半径更有利于提高低真空环境下仪器的灵敏度。

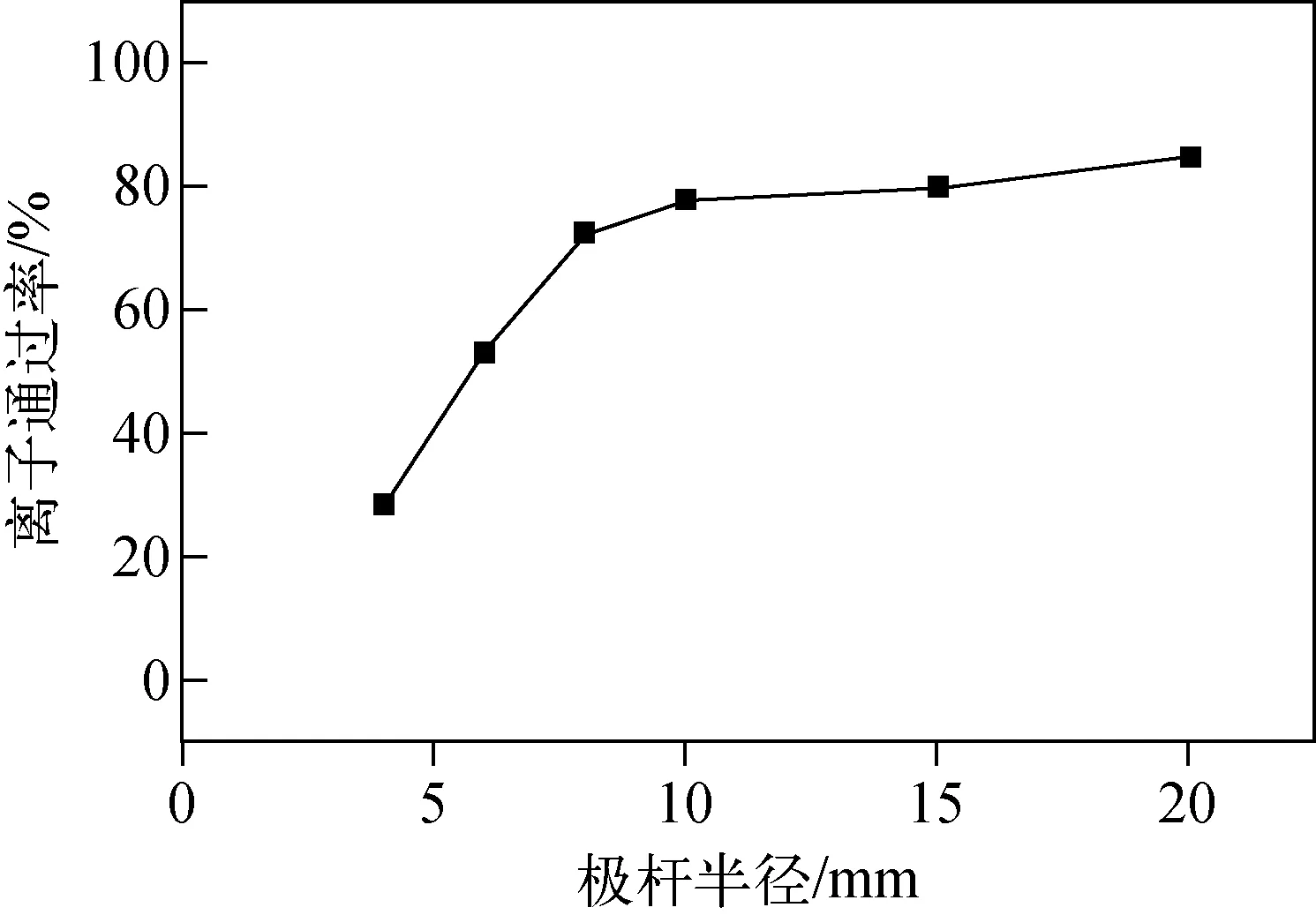
图10 四极杆半径re与离子通过率的关系Fig.10 Relationship between radius of rod and transmission probability

2.5 温度对灵敏度的影响

温度反映了离子运动的剧烈程度，当背景气体质量mg=4 u，背景气体压强p=3 Pa时，针对质量为40 u的离子，不同温度下的离子通过率示于图11。可知，温度升高，离子通过率增大，当温度由10 ℃升至200 ℃时，离子通过率提高近一倍。由式(5)可知，随着温度升高，碰撞频率降低，离子与背景气体的碰撞次数减少，其通过率提高。因此，在低真空下，升高温度有助于提高仪器的灵敏度。

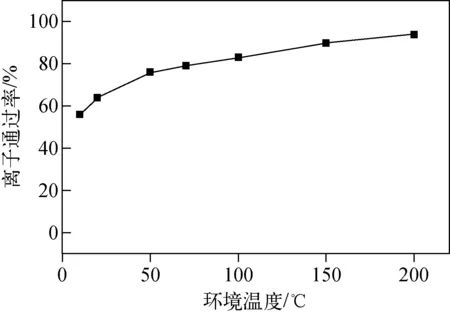
图11 环境温度与离子通过率的关系Fig.11 Relationship between temperature and transmission probability

3 结论

针对低真空条件下的质量分析，扩展了阻力模型，引入Langevin碰撞理论，利用有限元分析方法，在COMSOL Multiphysics中搭建了低真空环境下针对四极杆质量分析器的离子运动仿真平台。利用该平台研究了低真空环境下不同因素对四极杆质谱仪灵敏度的影响，得到如下结论：

1) 在低真空质量分析中引入Langevin碰撞理论，与阻力模型相比，可以更好地反映低真空环境下离子的运动情况；

2) 当真空度降低，离子与背景气体的碰撞频率增加，四极杆质量分析器灵敏度降低，但较大质量的离子更容易获得较高的灵敏度；

3) 通过使用质量较小的背景气体，在一定范围内增加离子的初始动能、增大四极杆的半径、提高操作温度等措施，可以提高低真空环境下仪器的灵敏度。

[1] GAO L, SONG Q, PATTERSON G E, et al. Handheld rectilinear ion trap mass spectrometer[J]. Analytical Chemistry, 2006, 78(17): 5 994-6 002.

[2] GAO L, SUGIARTO A, HARPER J D, et al. Design and characterization of a multisource hand-held tandem mass spectrometer[J]. Analytical Chemistry, 2008, 80(19): 7 198-7 205.

[3] LI L, CHEN T C, REN Y, et al. Mini 12, miniature mass spectrometer for clinical and other applications introduction and characterization[J]. Analytical Chemistry, 2014, 86(6): 2 909-2 916.

[4] ZHAI Y, FENG Y, WEI Y, et al. Development of a miniature mass spectrometer with continuous atmospheric pressure interface[J]. Analyst, 2015, 140(10): 3 406-3 414.

[5] SNYDER D T, PULLIAM C J, OUYANG Z, et al. Miniature and fieluble mass spectrometers: recent advances[J]. Analytical Chemistry, 2015, 88(1): 2-29.

[6] XU W, SONG Q, SMITH S A, et al. Ion trap mass analysis at high pressure: a theoretical view[J]. Journal of the American Society for Mass Spectrometry, 2009, 20(11): 2 144-2 153.

[7] SONG Q, XU W, SMITH S A, et al. Ion trap mass analysis at high pressure: an experimental characterization[J]. Journal of Mass Spectrometry, 2010, 45(1): 26-34.

[8] WHETTEN N R. Macroscopic particle motion in quadrupole fields[J]. Journal of Vacuum Science & Technology, 1974, 11(2): 515-518.

[9] HASEGAWA T, UEHARA K. Dynamics of a single particle in a Paul trap in the presence of the umping force[J]. Applied Physics B, 1995, 61(2): 159-163.

[10] WHITTEN W B, REILLY P T A, RAMSEY J M. High pressure ion trap mass spectrometry[J]. Rapid Communications in Mass Spectrometry, 2004, 18(15): 1 749-1 752.

[11] BUI H A, GRAHAM COOKS R. Windows version of the ion trap simulation program ITSIM: a powerful heuristic and predictive tool in ion trap mass spectrometry[J]. Journal of Mass Spectrometry, 1998, 33(4): 297-304.

[12] FORBES M W, SHARIFI M, CROLEY T, et al. Simulation of ion trajectories in a quadrupole ion trap: a comparison of three simulation programs[J]. Journal of Mass Spectrometry, 1999, 34(12): 1 219-1 239.

[13] LOCK C M, DYER E W. Simulation of ion trajectories through a high pressure radio frequency only quadrupole collision cell by SIMION 6.0[J]. Rapid Communications in Mass Spectrometry, 1999, 13(5): 422-431.

[14] 张晶晶,李明,姜杰,等. 基于有限元法的离子迁移谱电场数值模拟研究[J]. 质谱学报,2014,35(3):232-237.

ZHANG Jingjing, LI Ming, JIANG Jie, et al. Numerical simulation of electric field for ion mobility spectrometer based on finite element method[J]. Journal of Chinese Mass Spectrometry Society, 2014, 35(3): 232-237(in Chinese).

[15] GIBSON J R, TAYLOR S. Prediction of quadrupole mass filter performance for hyperbolic and circular cross section electrodes[J]. Rapid Communications in Mass Spectrometry, 2000, 14(18): 1 669-1 673.

[16] MARCH R E. An introduction to quadrupole ion trap mass spectrometry[J]. Journal of Mass Spectrometry, 1997, 32(4): 351-369.

[17] HE M, GUO D, FENG Y, et al. Realistic modeling of ion-neutral collisions in quadrupole ion traps[J]. Journal of Mass Spectrometry, 2015, 50(1): 95-102.