关于生产车间作业优化调度效率仿真研究

（兰州交通大学 交通运输学院，兰州 730070）

0 引言

车间调度效率的高低将直接影响产品的生命周期和企业的利益成本。1919年，由Gantt[1]率先使用甘特图表示车间调度的作业流程；1976年，Garey[2]等证明了该类组合优化问题属于NP完全问题；1998年，Egon[12]等从调度解邻居角度出发，提出的N6结构大大减少了在关键路径上做无效搜索的次数，减少了搜索时间同时保证了解的质量。由于作业车间调度问题较旅行商问题等其他NP问题更为复杂[14]，几十年来，求解该类问题的方法大多集中在非数值近似算法上，该近似算法大多为生物进化算法，分别有模拟退火算法[3]，遗传算法[4]，例子群算法[5]，禁忌搜索算法[6]，以及各类改进的生物进化算法和混合算法。例如，粒子群算法具有更新规则简单，编码易于实现且具有较快的收敛性等优点[7]，遗传算法和模拟退火算法具有搜索全局最优解的优点[8]。因此Min[9]等运用自适应的变异概率与全局退火的策略，提出遗传退火算法；李小涛[10]等提出基于染色体agent的邻居结构，结合模拟退火遗传混合算法求解车间调度问题。近年来，随着人工智能技术的兴起，Bagheri[15]等提出的人工免疫算法在和Wang[16]等提出的人工蜂群算法在求解作业车间调度问题上开始受到重视，求解精度质量大幅度提高。

随着车间调度问题的规模增大，求解该问题的难度和时间也将呈指数级别增加[2]，针对文献[9,10,15,16]在收敛性和计算时间上的不足，文中结合粒子群算法收敛性快的优点，提出粒子群遗传混合算法。本文的混合算法首先为了跳出车间调度问题解的大山谷结构[10]，提出以模拟退火操作中使用的Metropolis准则定义自适应的变异概率[9]，混合算法中再整合粒子群算法在局部邻域搜索最优解的优点，将该局部最优调度解作为染色体变异交叉的对象，在变异和交叉操作中再辅以改进的2变换邻域搜索[11]。最后仿真实例说明了该混合算法具有有效性和可行性的优点。

1 生产作业车间调度问题模型

1.1 生产作业车间调度系统描述

Egon[12]等提出作业车间调度问题是求解所有工件的所有工序在指定调度安排下最大完工时间最小值的过程。生产作业车间调度问题的已知输入条件有：加工机器集合工件集合工序集合工件pi的工序集合为工件加工时间集合工件pi的工序加工时间集合

由于生产作业车间调度问题需要同时考虑工件的加工时间和加工顺序，因此增加了求解此类组合优化问题的复杂性；且在实际生产调度中，需要考虑资源数量和设备容量等约束，同时该离散系统需要从离散问题优化角度入手。因此求解大规模生产作业车间调度问题将增加时间和空间消耗。本文在求解此类问题过程做出以下五点假定：

1）已知每个工件的每道工序在指定机器上加工；

2）已知每个工件的每道工序的加工时间，且为常数；

3）每个工件的工序加工顺序不能改变，即必须在前一道工序加工完成之后才能完成后一道工序，而对于不同工件的加工工序顺序没有顺序要求；

4）每台机器同时只能加工一个工件的一道工序，且机器在执行加工任务时不会发生故障；

5）机器加工工件没有时间等待，且每个工件只在机器上加工一次。

1.2 数学模型表达式

作业车间调度问题要求最大完工时间（makespan）[12]最小，因此结合模型假定，提出以下数学模型：

目标函数为式(1)：

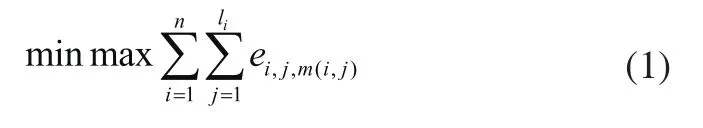
目标函数式(1)表示所有工件的所有工序在指定调度顺序下最大加工时间最短，其中ei,j,m(i,j)表示第i个工件的第j道工序在第m台机器上加工的结束时间；

约束条件为式(2)～式(5)：

式(2)为每个工件每道工序的结束加工时刻等于开始加工时刻加上对应工序的加工时间，其中si,j,m(i,j)表示第i个工件的第j道工序在第m台机器上加工的开始时间，Ti,j,m(i,j)表示第i个工件的第j道工序在第m台机器上加工的加工时间；

式(3)是每个工件前后加工顺序的约束条件，即每个工件后一道工序开始时间应大于该工件前一道工序的结束时间；

式(4)、式(5)是每台机器的约束条件，保证每一台机器上同一时刻只能加工一个工件的一道工序；

M表示一个无穷大的常数。

车间调度问题是一个典型的多约束优化组合问题，已经证明此问题属于NP完全问题，该类问题需要在现有调度解空间中迭代搜寻得到最优解。即使求解规模较小，求解质量与效率也都很难得到保证，为提高该类问题解的质量与搜索效率，本文采用改进的粒子群遗传混合进化算法，从而让总体目标函数达到最优。

2 基于自适应变异概率的PSO与GA混合算法寻优

2.1 个体编码方式

本混合算法采用基于工序的编码方式，每个个体均对应于一种调度方案。以n个工件，每个工件有m道工序为例，在该编码方式中，每个工件i出现m次，从前往后依次表示工件i的加工顺序。以3×3为例，参照表1的工序加工机器顺序，工序[1,3,2,1,2,3,2,1,3]中，第一个1表示工件1的第一道工序在机器2上加工，第二个1表示工件1的第二道工序在机器3上加工，第三个1表示工件1的第三道工序在机器1上加工。

表1 每个工件每道工序的加工机器

2.2 混合算法目标值定义

粒子群算法搜寻得到的局部最优解和遗传算法的适应值均对应指定调度下工件总完工时间，且应保证总完工时间最短。

2.3 PSO-GA混合算法操作思想

1）在遗传算法变异概率选择上，参照模拟退火中Metropolics[9]准则选择适当的变异概率，对交叉概率也需进行概率线性变换。

2）将粒子群算法寻求的局部最优调度解作为变异和交叉操作的对象，根据粒子群惯性权重w特点[13]，当w过大，粒子群偏向全局搜寻，而当w较小，粒子群偏向于局部搜寻，因此本混合算法对惯性权重w进行自适应计算。

3）对2变换邻域邻居结构进行改进。变异操作中，在1，2中随机产生一个随机数n，如果n=1，则变异位a,b之间的距离小于整条染色体的三分之一，将a,b两处的基因对调；如果n=2，则变异位a,b之间的距离没有限制，再将a,b两处的基因对调。交叉操作中，同样在1，2中随机产生一个随机数n，如果n=1，则交叉位a,b之间的距离小于整条染色体的三分之一，参与交叉的两染色体中从左往右，先将a,b之间基因相同的标记为0，并参与交叉操作，不为0的不参与交叉操作；如果n=2，则交叉位a,b之间的距离没有限制，按同样的方法即可实现交叉操作。

2.4 自适应变异概率计算

混合算法初期，为了加快个体变异，初期设置的变异概率pm较大[9]；随着个体适应度增加，以及为了加快计算速度，赋以变异概率自适应值，具体如下所示：

上式中η为常数，设为2，k为进化代数。

2.5 惯性权重自适应计算

将惯性权重设置为变量，有利于扩大对解空间的搜索，同时防止出现早熟的现象[13]。

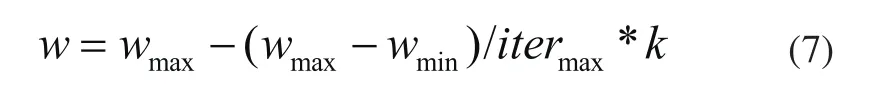
式中wmax为最大惯性权重，wmin为最小惯性权重，itermax为总进化代数，k为第k次进化。

2.6 改进2变换邻域邻居结构图例

1）以3*3的一个调度解作为例子，如图1所示，一条染色体编码为[3 1 2 3 1 2 1 2 3]。当随机产生的数值为2时，即发生变异的两个位置之间距离应没有限制，变异位置为2和6，将染色体上两变异位置对应的基因互换位置后即可得到新的染色体，新染色体对应的基因为[3 2 2 3 1 1 1 2 3]。

图1 当n=2时的变异操作

2）以3*3为例，选取两染色体分别为[3 1 2 3 1 1 2 3 2]和[1 2 2 3 1 3 1 2 3]，具体如图2所示，随机产生的交叉位置为2，即参与交叉两染色体交叉位置之间的距离没有限制，交叉位置分别为4和7。将两染色体从4位到7位从左往右将相同的基因先后置为0，处理后的两染色体基因分别为[3 1 2 0 0 0 2 3 2]和[1 2 2 0 0 3 0 2 3]，两染色体中基因为0位置处的原基因再参与交叉操作，交叉后的新染色体分别为[3 1 2 1 1 3 2 3 2]和[1 2 2 1 1 3 3 2 3]。

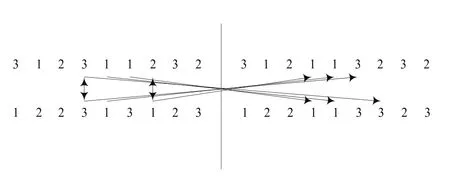
图2 当n=2时的交叉操作

3 仿真算例

仿真工具：Matlab R2014a；

仿真环境：win10操作系统；cpu：i5-6200u处理器，2.3GHz；12GDDR4内存。

3.1 参数设置

本混合算法种群大小为100，进化代数设置为100，pm为0.1，wmax为1.2，wmin为0.4。

3.2 测试结果分析评价

图3 算法流程图

通过对6组测试数据进行计算，且每组数据均进行10次运算，对最优解与时间分别取平均值后得到表2。

通过与测试数据[14]进行比对，混合算法得到的最优解与目前已知的最优解的平均误差分别为：0%，1.2%，3.7%，3.9%，4.9%，3.9%。

同时，混合算法得到最优解时间较目前得到已知最优解时间有大幅度提升。

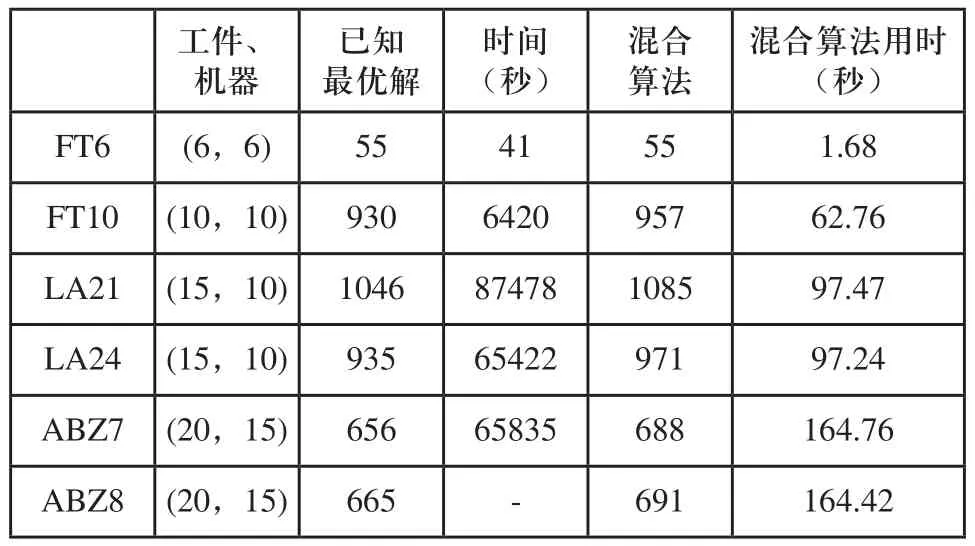
表2 混合算法与最优解数值、时间对比

以FT10类测试问题为例，绘出混合算法迭代次数与最优解的关系曲线图如图4所示。

由图4可以看出，混合算法收敛速度快，用时短，FT10类测试问题在17代就达到满意值，并且满足精度要求。

图4 FT10类混合算法仿真实例

为进一步论证该混合算法的有效性，将该混合算法得到的解与普通的粒子群算法与模拟退火算法得到的解进行对比，具体数值如表3所示。通过对比发现，混合算法得到的解均大幅度优于普通的粒子群算法和模拟退火算法得到的解。

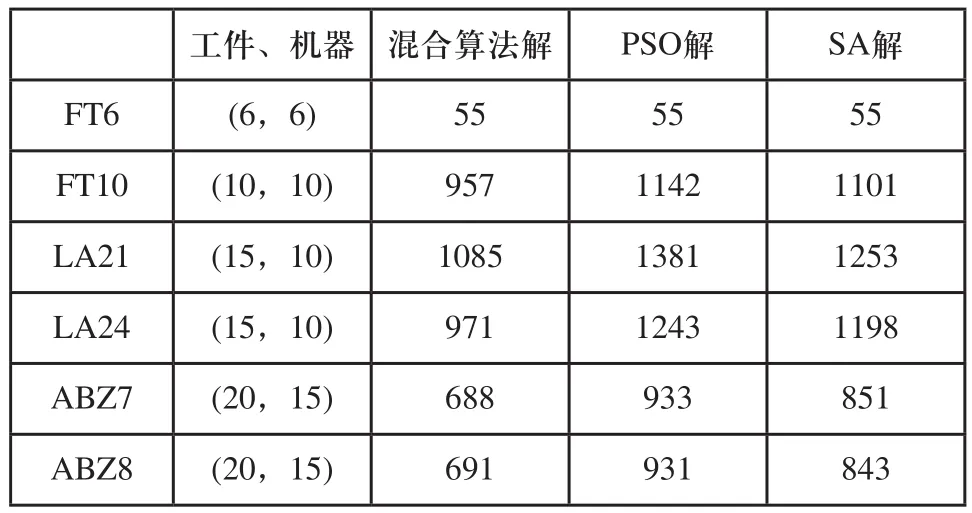
表3 混合算法与PSO,SA对比

以FT10为例，在迭代次数为2000条件下，将粒子群算法和模拟退火算法的迭代次数与最优解的关系曲线图绘出，如图5所示。可以看到普通PSO与SA收敛速度较混合算法更慢，PSO需要在1087代才能收敛，SA需要在1291代才能收敛，且PSO得到的解1142和SA得到的解1101较混合算法得到的解957更差，且精度更低。

图5 FT10类SA,PSO仿真实例

4 结论

通过参考模拟退火操作中Metropolics准则定义自适应的变异概率，很好地解决了车间调度问题解的大山谷结构的问题，从而可以让解跳出局部最优；同时定义自适应的惯性权重值，使得粒子群得到的局部最优解向全局最优解靠拢；得到的局部最优解在变异交叉中辅以改进的2变换邻域操作，进而充分体现了优化算法中解的扩散策略。

通过与3类6组经典测试数据已知的最优解进行比对可以发现，本混合算法得到最优解与目前已知的最优解平均误差均在5%以内，且计算时间有大幅度提升；同时混合算法得到的最优解与普通的粒子群算法和模拟退火算法得到的最优解进行对比可以发现，混合算法的最优解具有明显的优势。前后两次仿真结果对照均论证了该粒子群遗传混合算法具有有效性和可行性的优点。

[1]A.S. Jain,S.Meeran. Deterministic job-shop scheduling: Past,present and future[J].European of Operational Research,113,1999.390-400.

[2]Garey M.R., Johnson D.S.,Sethi R. The complexity of flow shop and job-shop scheduling[J].Mathematics of Operation Research,1976,1(2).117-129.

[3]Van Laarhoven P.J.M., Aarts E.H.L.,Lenstra J.K. Job shop scheduling by simulated annealing[J].Operation Research,1992,40(1).113-125.

[4]Yamada T.,Nakano R.A genetic algorithm with multi-step crossover for job-shop scheduling problems[J]. Proceedings of Int.Conf. on GAs in Eng. Sys.,1995b.146-151.

[5]Sha D.Y.,& Lin H.H. A multi-objective PSO for job-shop scheduling problems[J].Expert System with Applications,2010,37(2).1065-1070.

[6]Nowicki E., Smutnicki C.A fast taboo search algorithm for the job-shop problem[J]. Management Science,1996,42(6).797-813.

[7]Wer-Der Chang.A modified particle swarm optimization with multiple subpopulations for multimodal function optimization problems[J].Applied Soft Computing,2015(33).170-173.

[8]Maniezzo V.Genetic evolution of the topology and weight distribution of neural network[J].IEEE Transactions on Neural Networks,1994,5(1).54-65.

[9]Min Liu,Zhi-jiang Sun,Jun-wei Yan, Jiong-song Kang.An adaptive annealing genetic algorithm for the job-shop planning and scheduling problem[J].Expert Systems with Application,2011,38.9248-9254.

[10]李小涛,彭翀.基于混合多智能体遗传算法的作业车间调度问题研究[J].北京航空航天大学学报,2017,43(2).410-416.

[11]赵良辉,邓飞其.用于作业车间调度的模拟退火算法[J].制造业自动化,2006,28(3).10-12.

[12]Egon Balas, Alkis Vazacopoulos. Guided local search with shifting bottleneck for job shop scheduling[J].Management Science,1998,44(2).262-270.

[13]Yannis Marinakis, Athanasios Migdalas, Angelo Sifaleras. A hybrid particle swarm optimization – variable neighborhood search algorithm for constrained shortest path problems[J].European of Operational Research, 2017,261.819-823.

[14]王凌.车间调度及其遗传算法[M].清华大学出版社,2003,56-67.

[15]Bagheri, A., Zandieh, M., Mahdavi, I., Yazdani, M. An artificial immune algorithm for the flexible jos-shop scheduling problem[J].Future Generation Computer Systems,2010,26(4).533-540.

[16]Wang, L., Zhou, G., Xu, Y., Wang, S., Liu, M. An effective artificial bee colony algorithm for the flexible job-shop scheduling problem[J].The international Journal of Advanced Manufacturing Technology,2011.1-13.