考虑弹性结构时桥式起重机防摇控制系统数学建模方法研究

（同济大学 机械电子研究所，上海 201804）

0 引言

大多桥式起重机防摇控制策略的研究中，数学模型的建立及数学建模方法的研究是基础与前提。在以往对桥式起重机数学模型研究中，通常把桥式起重机的运行机构假象为刚性结构并建立了双质量两自由度的系统模型。文献[1]中已经建立起以电机频率为输入的小车-吊重系统的双质量两自由度的桥式起重机动力学模型[1]。这样的假定在大多数情况下比较合理[2,3]。但起重机在大车运行过程中，起重机主梁会产生垂向变形和横向变形，这些弹性变形的影响在双质量两自由度的系统模型中无法体现。考虑到采用状态观测器[4]、软测量[5]等方法进行防摇控制的策略，由于吊重摆角不易测量或测量实现的成本较高而需要借助其他可测变量转化为摆角信息。这类控制方法的比较依赖于桥式起重机模型的精确性，模型的精确性越高，防摇控制的效果越好。本文建立系统动态分析模型，考虑起重机主梁的横向变形，得到桥式起重机运行机构为弹性结构时系统动力学方程[6]，并与传统双质量两自由度的系统模型进行对比，以获得运行机构弹性结构在起重机动力学简化系统的影响关系。

1 起重机运行机构系统模型

起重机运行作业时会引起主梁的垂向变形和横向变形，为了起重机防摇控制的模型研究，从防摇控制角度考虑，只需分析起重机主梁的横向变形在模型方面的影响。假定桥架结构在弹性范围内变形且不考虑风载的影响。对大车桥架系统进行分析时，假定只有大车的运动，小车是固定在大车上静止不动的。对于横向变形，起重机支腿在运行方向的刚性较小可以忽略。起升机构传动零件（包括电机转子）转动惯量转化至车轮周向的质量远大于结构的换算质量需要在数学建模时考虑。另外，与吊重相比，钢丝绳质量很小，将它抽象为无质量的单元。因此，当考虑车架为弹性结构时，起重机系统可简化为图1所示的三质量三自由度的串联弹性动力学系统模型。

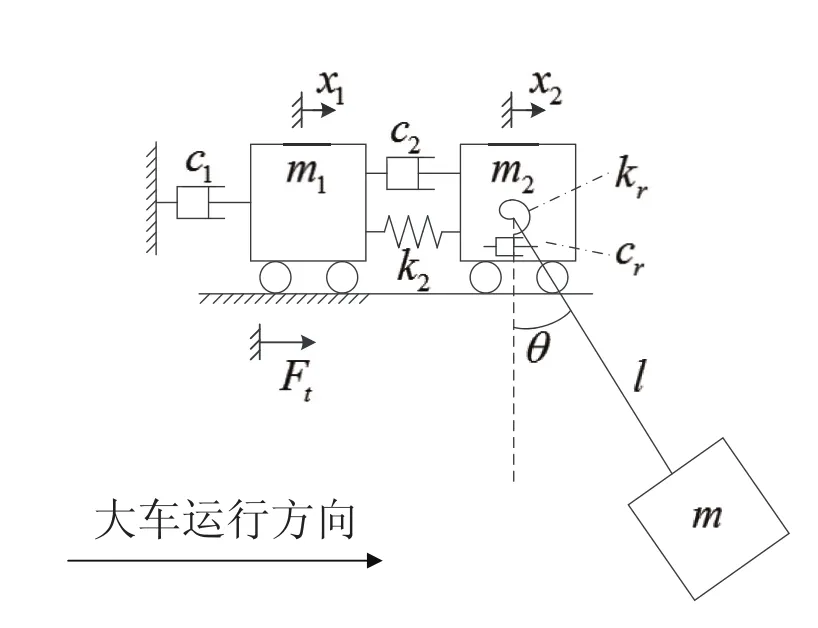
图1 桥式起重机运行机构力学模型

图中，m1由三部分质量构成：

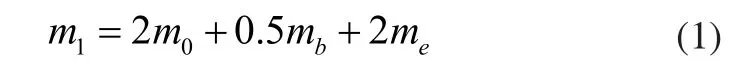
式中，me为一侧端梁的总质量（包括其上的运行装置的质量）；mb为起重机桥架主梁的总质量（包括走台、栏杆等质量）；m0为一侧运行机构旋转件转动惯量转化到车轮周向的等效质量。

m2包括主梁在跨中的等效质量及小车的质量：

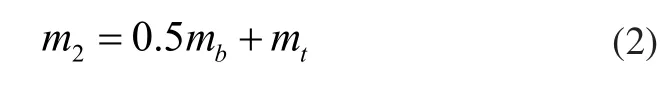
式中，mt为小车的自身质量。

m为吊重的质量。

c1为驱动电机、减速器及传动机构等机构内的摩擦，c2为金属结构变形与空气产生的综合阻尼，cr为钢丝绳内部多根钢丝之间相互滑动产生的阻尼；k2为起重机考虑横向变形时主梁的刚度，kr为由于钢丝绳僵性产生等效刚度。

2 动力学系统微分方程组的建立

由于本文研究的是弹性系统在静平衡位置附近的微小振动，刚度系数与位移x无关，另外m，c，k也与时间无关。设m1，m2质量位移x1(t)，x2(t)的坐标原点在静平衡位置，吊重m的位移x是相对于x2的相对位移。当大车以某一速度运动时，系统中所有质量都参与运动。分别对m1，m2，m进行如图2起重机运行机构受力分析所示，并得到方程式(3)。

图2 桥式起重机运行机构受力分析

式中，Fr为钢丝绳的拉力，通过受力分解可以得到

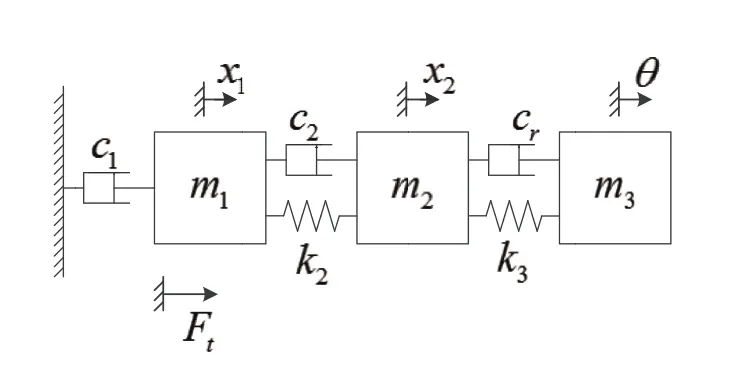
图3 桥式起重机运行机构等效力学模型

最后分析Ft的取值。在实际应用中，桥式起重机一般用变频器-三相交流异步交流电动机进行驱动。异步电动机的转速与转矩的机械特性曲线如图4所示。通常三相异步电动机都工作在所示特性曲线的额定转速及额定转速附近。可以发现，此时转速与转矩呈线性变化，可以线性化为图中虚线所示。由图4同样可以看到当改变电机输入频率时，电机的机械特性曲线只随之上下平移，斜率保持不变[7]。在研究中将交流电机转速转矩曲线进行线性化，由（0，n0）和（TN，nN）两点，可以得到其斜率。

图4 异步电动机机械特性曲

R为小车车轮半径；

p为电动机旋转磁场极对数。

最后由多轴拖动的运动方程[8]，将负载折算到电机轴的负载转矩，得到电动机的驱动力：

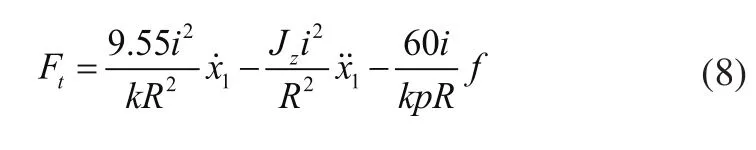
式中，JZ为系统折算到电机轴上的转动惯量，并记

图2中所示的三质量三个自由度弹性质量系统建立振动微分方程组矩阵形式如式(9)所示，由于式(7)Ft中包含了将与有关的项移到运动方程的左边，前的系数构成了与振动分析中的粘性阻尼系数相似的系数。

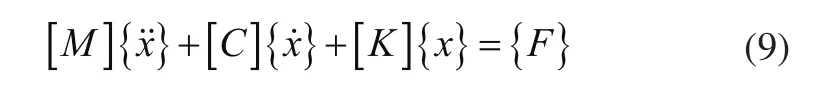
由式(4)与式(8)联立整理得，

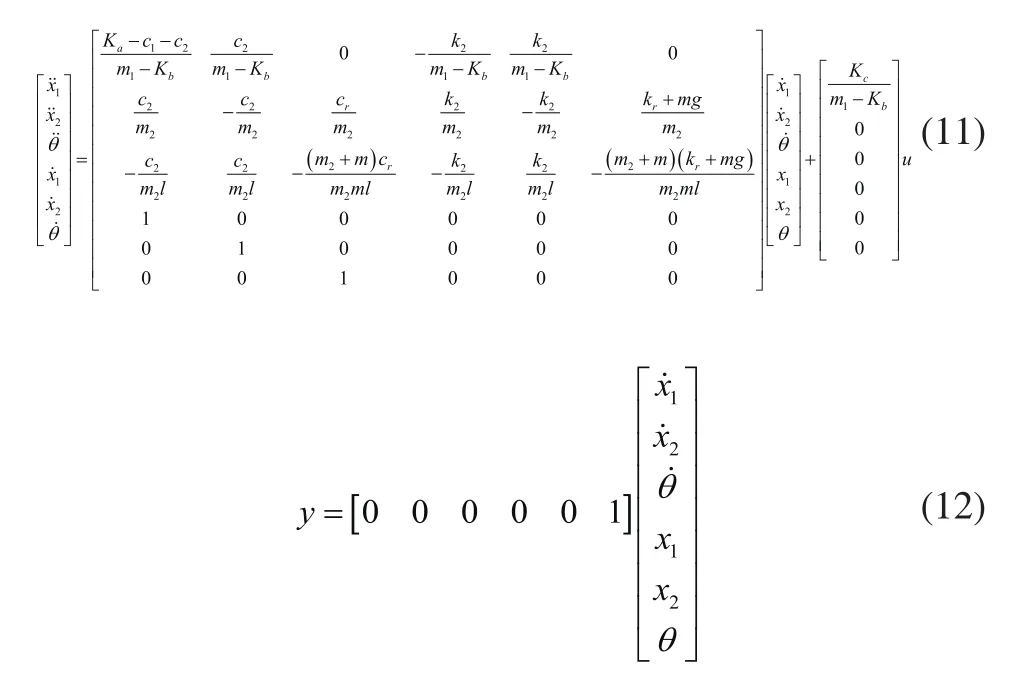
3 基于MATLAB的仿真对比

由上一节得到桥式起重机数学模型系统状态图如图5所示，其中A为x的系数矩阵，B为输入u的系数矩阵，矩阵C将系统输出转化为摆角。

根据振动微分方程组矩阵方程式(9)建立MATLAB/SIMULINK仿真模型。仿真中以QD32/8-22.5A5通用型桥式起重机为对象，主要参数为：小车质量mt=4839kg，桥架主梁总主梁质量mb=1323kg，一侧端梁总质量me=1392kg，一侧运行机构旋转件转动惯量转化到车轮周向的等效质量m0=400kg，吊重质量取为M=10t，跨度L=22.5m，绳长取l=8m，主梁的横截面积为A=91700mm2，主梁弹性模量为E=2.1×105MPa，钢丝绳型号为16NAT6×19W+FC1770。

将三质量系统和传统的双质量系统[1]（只考虑小车和吊重）进行对比。图6所示为两个系统对应摆角的系统输出。由图6(a)可见，三质量相对于双质量系统摆角摆动的固有频率更高，振动的振幅更小，摆角的衰减速度更慢。在前10秒内，两个系统相位基本一致，三质量系统最大摆幅与双质量系统相差10.4%。随着时间推移，双质量系统相位逐渐落后于三质量系统，在30秒左右时，双质量系统落后三质量系统π/2的相位。由图6(b)可见，前15秒内，两个系统的摆角误差较大，三质量系统的摆角幅值最大减小了约0.38弧度，相对于双质量系统，三质量系统摆角误差最大达22.0%。15秒之后，双质量系统与三质量系统摆角差值逐渐随时间减小。

4 结论

【】【】量模型慢。因此对长时间的防摇控制，以准确的摆角反馈来实现防摇策略时，采用三质量模型摆角估算更精确，防摇效果更佳；3）c1，c2，cr，k2，kr五个参数中，kr的取值会对摆动的频率和幅值产生较大的影响。kr越大，摆角摆动频率越高，摆幅越小。当钢丝绳的僵性产生的等效刚度较大时，桥式起重机系统应采用三质量三自由度动力学系统模型。

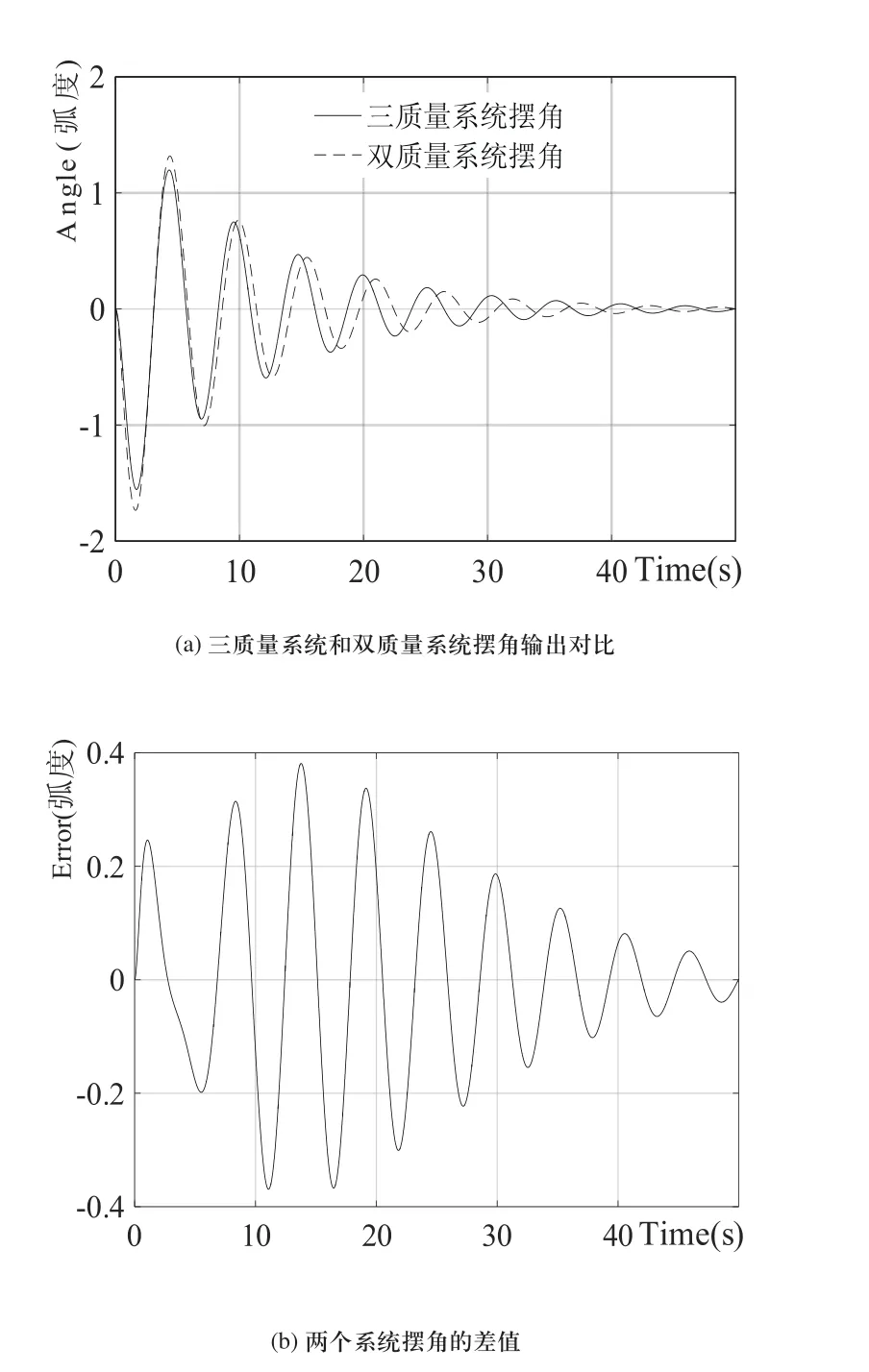
图6 两系统对应摆角θ的系统输出对比

[1]王璐,常中龙,袁哲,等.桥式起重机防摇控制系统数学建模方法研究[J].起重运输机械,2016(9):1-5.

[2]Neugebauer R. Dynamischein Laufkranen beim Anheben and Abbremsen der Last[M]. Der stahlbau.1957:16-21.

[3]Lightfoot E,Clarkson B L.Dynamic stresses in E.O.T.cranes due to the hoisting and lowering of loads[J].Material Handling Mechanics.1955:169(10):223-22.

[4]钟斌.基于吊重防摇控制的起重机快速对位关键技术研究[D].西南交通大学,2007.

[5]岳文翀,鄢鹏程,唐超隽,等.基于软测量技术的桥式起重机防摇控制方法研究[J].起重运输机械,20π17(1):55-58.

[6]程文明,邓斌,王金诺.小车架为弹性结构时门式起重机的动态特性研究[J].西南交通大学学报,2001,36(2):144-148.

[7]秦曾煌,姜三勇.电工学（第七版）上册[M].高等教育出版社,2009:228-238.

[8]冯清秀,邓星钟.机电传动控制[M].5版.华中科技大学出版社,2011:5-10.