鞋底生产过程优化排产模型研究

杨 伟，曾隽芳，2

（1.中国科学院自动化研究所，北京 100190；2.北京三博中自有限公司，北京 100190）

国内鞋底企业生产计划的制定和排产主要靠人工来完成，大部分企业将能在规定的时间内完成相应的生产任务视为合格的生产计划，生产设备使用率、生产率低，生产成本居高不下，既没有最大程度地凸显生产设备的先进性，同时也难以在激烈的市场竞争中取胜。少数企业则采用了ERP（enterprise resource planning）系统[1]。ERP系统支持和加快了订单的整个处理过程，使业务和生产过程管理实现数据共享和集成，实现事务处理自动化和对财务、生产和分销资源进行跟踪，改进企业的灵活性和提高应变能力。但是ERP系统有其局限性，不容易适应订单需求调整、资源容量、原材料可用性等变化，使得生产车间出现了许多问题，为了克服这些缺点，使用先进生产计划与调度系统[2]就非常必要。它是对生产过程进行规划与控制，合理安排企业的生产执行路线、任务执行的起止时间和对各种资源的调配等，先进的排产调度算法对生产过程运行的结果和经济效益起着决定性的作用。

对于鞋底生产企业，这是面向订单的多工序的生产方式，就是按照客户订单来安排生产，确定订单执行顺序后，再分解订单到各个车间进行生产，该生产方式对企业生产排产能力有较高要求，文献[3]对此类问题进行了分析。由于订单生产排序计划问题（简称排序）具有NP-HARD计算复杂性[4]，常规方法需耗费很大的计算量，近年来，一些新的启发式算法如遗传算法[5]、神经网络[6]、禁忌搜索[7]、粒子群算法[8]以及蚁群算法[9]也常用来解决这类调度问题。蚁群算法是由Dorigo[10]在1992年提出的一种模拟进化算法，在解决组合优化问题上有非常好的效果。由于鞋底生产过程也是一个多工序的车间调度问题，此类问题可以看做一个图模型的组合优化问题，图上每个节点代表一道生产工序，这使得使用蚁群算法非常适合解决此类问题。

本文对鞋底生产工艺进行分析，建立鞋底的生产计划与调度框架，提出基于多工序订单排序模型，应用蚁群算法进行求解，获得了优化后的排产计划，指导企业进行生产。

1 鞋底生产工艺

鞋底生产主要分为3个流程。大底生产和中底生产分别在大底车间以及中底车间中生产，这两者可以并行生产而不受工艺顺序影响，而贴合工艺就是将前两者的半成品进行加工贴合形成鞋底成品的过程，其工艺流程如图1所示，下面对工艺流程进行详细分析。

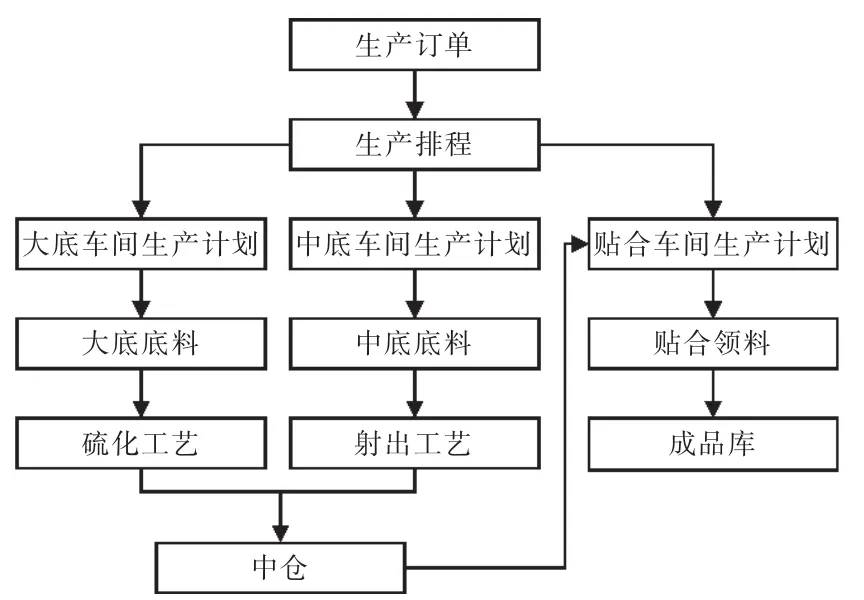
图1 鞋底生产工艺流程Fig.1 Flow chart of sole production

鞋子主要是由帮面、内衬（里子）、前后烫底、前后包头、中底（也叫寸底）、大底（鞋底）等部分组成，本文主要就鞋底生产中的中底、大底及其贴合工艺进行分析。

生产订单下达后，根据生产排产的计划，分别生成大底车间计划、中低车间计划和贴合车间计划，并分配相应的物料进行生产。大底车间的工艺流程包括前期对原材料进行预处理、截断等操作，然后再进行硫化、修边，生产完成后要清点统计数量再运往中仓等待下一步工艺处理。

中底车间主要针对EVA（醋酸乙烯共聚物）鞋中底，也称为一次发泡中底，是利用一次射出成型机来进行生产，该射出机将EVA树脂颗粒直接射入机台模具里面，真空加硫大约400 s后模具打开，模内鞋底发泡成型，再经过热、冷定型定。经过修边、分码、清点操作后运往中仓等待下一步工艺。该中底生产方法最大特点是产量高、一次成型，这也是目前最先进的EVA底生产技术。

贴合车间生产主要将中仓里的大底和中底进行贴合操作。经过打磨、水洗最后按订单码放并贴上标签运往成品库，完成该订单生产。

2 鞋底优化排产三级框架

优化排产是在考虑能力和设备的前提下，安排各生产任务的生产顺序，优化生产顺序，优化选择生产设备，以减少等待时间，平衡各机器和工人的生产负荷，从而优化产能，提高生产效率，缩短生产周期。根据企业生产实际情况，企业先得到销售合同订单，并将其订单信息录入ERP系统中，包括交货日期、所需模具、预期收益等，然后合理安排订单生产顺序使得企业收益最大。在企业MES（manufacturing execution system）系统中保存着车间生产约束如设备数量、模具数量、人工日历等约束信息，在将订单分解下达到车间后根据生产约束制定合理的车间生产计划，并通过车间看板、条码等信息进行反馈从而修正排产计划。

根据流程，本文将鞋底的排产分为3个等级，即订单计划系统、订单排产系统以及车间生产调度系统，图2所示为设计的鞋底三级排产框架。在排产中，还需要考虑紧急订单插入、质量问题以及设备故障等突发事件的处理，要根据实际生产状况调整生产调度计划。

图2 鞋底排产的三级框架Fig.2 Planning and scheduling structure design of sole production

2.1 订单计划系统

鞋底的订单主要是根据企业的销售合同、销售预测，为了减少库存以及排产难度，平衡所有生产能力，选择生产计划的时间跨度为一个季度，即需要给出企业一个季度的生产排产计划，指导企业进行生产，并在有新订单需要生产时，重新进行排产得到新的排产计划，当把订单计划下达给订单计划系统后，订单计划系统还需根据订单量采购需要的原料以及安排生产所需要的模具。

2.2 订单排产系统

鞋底排产主要是基于订单进行生产，是由订单驱动的生产方式。如何合理安排订单的生产顺序是订单排产的关键问题，本节将对订单排产问题进行分析。

在订单排产过程中，还需要考虑到相同订单以及紧急订单插入时的处理方法，相同订单是指虽然订单来自不同的公司，但是他们需要的鞋底都使用相同模具进行生产，那么当两者的交货期相差不远时，可以对这2个订单进行合并当作1个订单来进行生产。紧急插单是指当一个交货时间短并且订单优先级比较高时我们需要优先安排该订单生产。

由于鞋底生产需要经过大底、中底、贴合3个工序，所以订单需要在这3道工序中处理完成后才能交给客户，每个工序的设备在同一时刻只能生产同一订单，每个订单包含交货期、订单量、收益以及生产量，每道工序的处理时间可由车间调度系统反馈得到。当订单的完工时间晚于交货期时，企业需要承担延迟处罚，不同订单根据重要程度有不同的延迟惩罚系数。

2.3 车间生产调度系统

地方车间生产调度系统根据订单信息将订单分解得到需要生产的中底以及大底数量。由车间模具数量、设备数量等约束信息可以求得各个工序生产所需要的时间，结合订单调度系统，就可以得到各个生产车间的排产甘特图，指导生产。由于在生产过程中难免会出现一定的废品率，所以需要将信息反馈给订单计划系统，让其修正生产计划，重新排产。

从鞋底的生产工艺中可以看出，在大底车间和中底车间分别生产完成大底、中底半成品后，将产品运往中仓库进行存储，然后再运往贴合车间进行贴合工艺得到成品鞋底，最后再运往成品库中进行存储。中仓将大底、中底的生产和贴合工艺进行分开，减少了和贴合工艺之间的耦合。并且在这3道工序中，大底、中底生产可以并行执行，2个工序之间没有前后顺序约束，而贴合工序需要在大底中底生产完成后才能进行。车间调度系统的难点主要在于合理安排大底、中底以及贴合车间的生产。

由订单调度系统得到所要生产的订单顺序后，将订单生产计划具体细化到每一道工序，得到各个工序的起始时间和结束时间。在车间调度系统中，主要的约束有如下3个方面：

模具生产约束由于中底生产采用一次射出成型机，射出机配上不同模具才能生产各种中底，模具数影响了生产产能。所以该过程中使用的模型信息量非常重要，模具通过其型体编号和号码来进行分类，不同的订单所需要的模具并不相同，在该企业中，通过记录模具库存与模具计划数就可以得到每天可用的模具数。

设备使用约束在车间中一共有n条生产线，每条生产线2台射出机设备，每个设备都需要配备1个模具进行生产，设备数与模具共同决定了当天鞋底的产能。

工厂日历约束车间生产需要考虑工厂人员的可使用情况，该鞋底生产车间中，员工休息日将不进行生产，生产计划将按顺序延后生产。

3 基于蚁群算法的模型求解

3.1 订单计划系统

根据第3节中对鞋底生产排产框架的描述，以最大化企业收益为目标函数，则鞋底生产优化排产的数学模型为

目标函数：

约束条件：

式中：f为企业收益函数；n为工厂某时刻待排产订单数；m为订单需要处理的工序数，m=3；Ri为订单i的期望收益；wi为订单i的延迟惩罚系数；di为订单i的交货期；Cij为订单i在完成工序j时的时间；Tij为订单i在工序j上的处理时间；s（k）为在对n个订单的一个可行的订单处理顺序中，第k个被处理的订单。

式（1）为企业的收益函数，每个订单的实际收益为期望收益减去延迟惩罚，企业的总收益为各个订单实际收益之和；式（2）表示在处理订单s（k）时，之前订单的所有工序必须全部完成；式（3）表示在处理某个订单时，最后一道工序必须在前2道工序都处理完成后才能处理，而且前2道工序之间没有先后约束关系，可以同时生产；式（4）为订单处理初始化约束。

3.2 蚁群算法求解策略

蚁群算法ACA（ant colony algorithm）是一种模拟进化算法，启发于蚂蚁觅食的最短路径原理：在蚂蚁觅食过程中会释放一种特殊的分泌物——信息素，并因此影响蚂蚁的行为，当一条路径上经过的蚂蚁数量越来越多，留下的信息素也越多，使得后来的蚂蚁选择此条路径的概率越来越大，从而进一步增加了该路径上的信息素浓度，利用这种正反馈机制，蚂蚁最终能够在蚁巢和食物源头之间找到一条最短路径。蚁群算法的求解流程如图3所示。

（1）参数初始化。设置算法迭代次数N以及蚂蚁数N_ant，初始化信息τ（i，j）=C，C为较小的常数。

（2）蚂蚁根据状态转移概率选择下一个节点，转移概率为

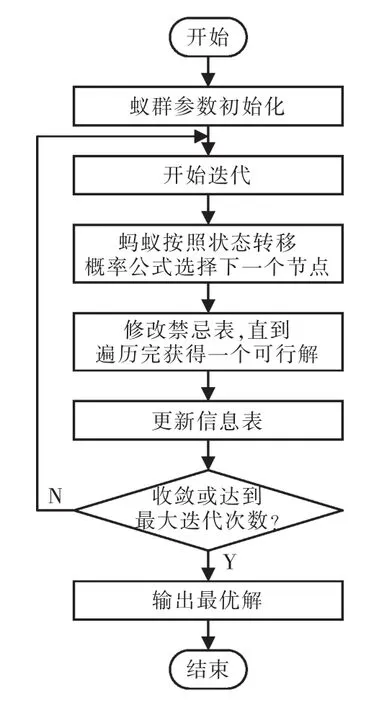
图3 蚁群算法流程Fig.3 Flow chart of ACA

（3）更新信息素，经过一次迭代之后，信息素为

式中：ρ为信息素的挥发系数，0≤ρ≤1；H为经过（i，j）的蚂蚁集合；L（k）为蚂蚁k因为延迟交货造成的惩罚；Δτ（i，j）为本次迭代中信息素增量。

（4）循环（2）、（3），直到算法收敛或达到最优解，该最优解对应蚂蚁的禁忌表中订单的顺序即是得出的最优的排产方案。

3.3 仿真验证

为了验证上述模型的正确性，以一项实际工程项目某鞋底制造企业为例。考虑该企业在一个生产加工调度周期内排产池中有10个订单，表1为订单中3个工艺的加工时间、收益、延迟惩罚以及交货期的表格，pa为大底工序所需时间，pb表示中底工序所需时间，pc表示贴合工序所需时间。

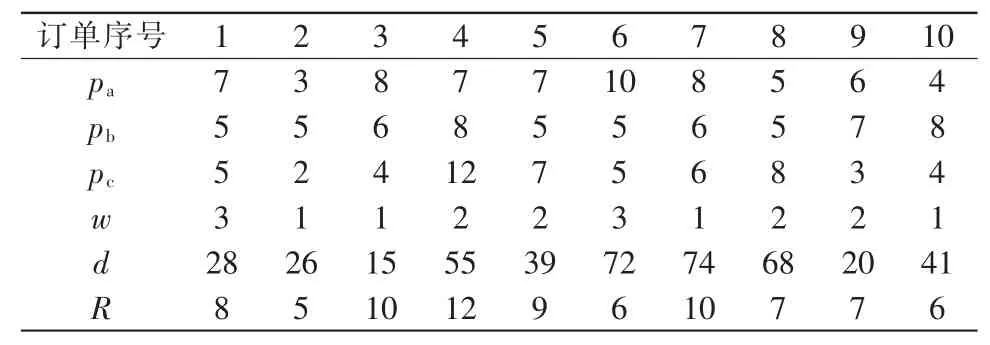
表1 订单排产信息表Tab.1 Order attribute information

对该优化问题利用蚁群算法进行求解，在Matlab中进行仿真，设置参数N_ant=20，N=500，α=1，β=2，ρ=0.1，Q=50，C=1。运行程序，得到的最优解为74，此时订单排产结果如图4所示，图中序号表示执行的订单编号，则利用此甘特图可以对鞋底生产过程进行有效指导。

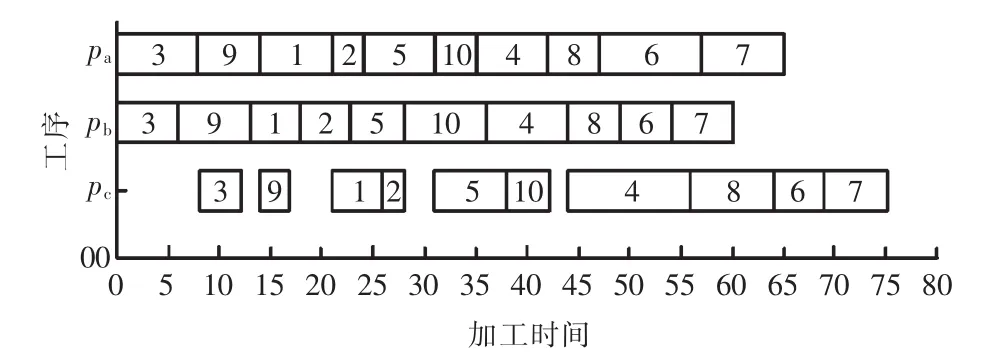
图4 鞋底排产甘特图Fig.4 Gantt diagram of sole scheduling

4 结语

本文根据鞋底生产工艺，建立了鞋底生产计划与调度的框架，对鞋底生产中大底、中底以及贴合等工艺过程进行了分析，提出了基于订单排产以及车间排产的分级排产模式，以最大化企业利润为目标建立模型并利用蚁群算法求解，得到排产计划的甘特图。本方法有效地利用了企业现有的资源，合理地安排订单生产，直观指导车间生产，部分研究成果已在某鞋底生产企业中得到应用验证。本模型为鞋底生产的复杂生产提供了排产支持，为企业创造更好的效益。

[1] Umble E J，Haft R R，Umble M M.Enterprise resource planning：Implementation procedures and critical success factors[J]. European Journal of Operational Research，2003，146（2）：241-257.

[2] Maravelias C T，Sung C.Integration of production planning and scheduling：Overview，challenges and opportunities[J].Computers &Chemical Engineering，2009，33（12）：1919-1930.

[3] 刘永，李言，李淑娟，等.面向订单的生产计划与调度的综合优化[J].工业工程与管理，2009，14（3）：84-89.

[4]De P，Ghosh J B，Wells C E.Job selection and sequencing on a single machine in a random environment[J].European Journal of Operational Research，1993，70（3）：425-431.

[5] Cheng C，Yang Z，Xing L，et al.An improved genetic algorithm with local search for order acceptance and scheduling problems [C]//Computational Intelligence in Production and Logistics Systems，IEEE，2013：115-122.

[6] Fang Xi，Chen Jing.A neural network model for resource scheduling optimization[C]//The IEEE International Conference on Information Management and Engineering.IEEE，2010：430-432.

[7] Cesaret B，Oĝuz C，Salman F S.A tabu search algorithm for order acceptance and scheduling[J].Computers&Operations Research，2012，39（6）：1197-1205.

[8] Liao Chingjong，Tseng Chaojong，Luarn P.A discrete version of particle swarm optimization for flowshop scheduling problems[J]. Computers&Operations Research，2007，34（10）：3099-3111.

[9] 王雪峰，陈志祥.用混合蚁群算法求解多工序订单生产计划[J].价值工程，2009（6）：5-8.

[10]Dorigo M，Caro G D.Ant colony optimization：a new meta-heuristic[C]//Evolutionary Computation，1999.CEC 99.Proceedings of the 1999 Congress on.IEEE，2002：1477 Vol.2.