基于有序图像的快速三维重建

刘保江，尹颜朋

（四川大学计算机学院，成都 610065）

0 引言

计算机三维重建技术是当前研究的一个热点。三维重建目的是从输入的多张二维场景图像恢复出场景三维立体模型。与传统的利用激光扫描仪等精密设备直接测量出物体三维模型相比具有方便、成本低以及适用范围广等优点，在文物考古、医疗卫生、旅游、数字娱乐和军事测绘导航等各个领域应用广泛。

进几十年来出现了许多基于图像视觉的三维重建方法，例如明暗度法[1-3]、纹理法[4-6]、轮廓法[7-8]、运动法[9]、调焦法[10]、双目视觉法[11]和多目视觉法[12]等。但是大都存在重建精度较差、鲁棒性较差问题，或是重建效果不错，但存在运算时间太长问题。故如何在达到不错的重建质量基础上提高重建速度就显得十分重要。

针对上面提出的方法存在的问题，本文提出一种基于有序图像序列的快速三维重建方法，在三维重建过程中，仅对相邻的图像进行特征匹配，对于n张输入图像，能够将匹配阶段的时间复杂度从O（n2）降低到O（n），对于大场景的重建在时间上节省尤为明显。然后利用多视图几何和对极几何约束关系，计算出场景的几何结构和摄像机的参数信息，重建出场景的三维立体模型，并使重建质量达到传统的三维重建的水平。主要包括三个步骤：相邻图像匹配、增量重建、点云优化。

1 算法实现

输入图像时，要保证输入图像是有序序列，即任意两张相邻的图像为需要重建的图像。在相邻图像匹配前，需要先确定摄像机内部参数。本文采用读取EXIF信息方法，因为许多摄像机的焦距和其他信息存放在图像的EXIF信息中，先通过对图像的EXIF信息解析得到相机的内参K，虽然并不一定精确，但可以将其作为摄像机的初始内参，然后在后续重建过程中对摄像机内参K进行优化。

1.1相邻图像匹配

检测所有图像中的特征点是匹配的第一步。本文采取的是SIFT方法[13]，总体思想为：首先对图像I（x,y）构造尺度空间：

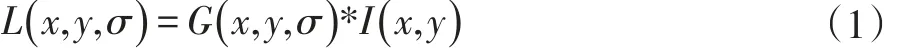
进一步得到高斯差分尺度空间：

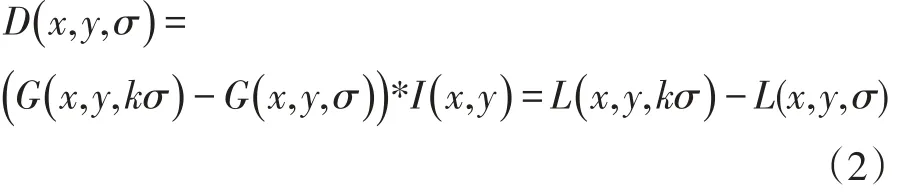
其中G(x ,y,σ ) 是尺度可变高斯函数，D(x ,y,σ)是高斯差分尺度空间。然后检测尺度空间中极值点，将检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2共26个点比较，若为最大值或最小值就认为是特征点。接着去除不好的特征点，然后将特征点赋值128维的方向参数，用以生成特征点描述子。完成特征点检测后，对两图匹配图像，通过特征点描述子之间的距离计算可得到匹配的特征点对。

传统的重建方法在此处会对任意的两张图像进行匹配，匹配的结果用于后续求同一三维空间点在各图像上对应的特征点序列和反投影求三维空间点。本算法在此处只对相邻的图像进行匹配。对于N张输入图像，传统方法共需要进行N*（N-1）/2次匹配，而本算法只需要进行N-1次匹配。故对于较大的N，此处节省的时间尤为明显。

1.2 三维重建

三维重建的过程是一个增量重建的过程，先对前两幅图像进行重建，然后按输入图像顺序依次对加入图像进行重建。对于任何两张图像重建过程如下：

先根据对极几何约束通过匹配点对求出基础矩阵F:

其中x1和x2为两图上对应的匹配点。由上式可知最少需要8对点可求得F矩阵，然后通过基础矩阵F得到essential矩阵E:

其中K’和K分别为两图对应的摄像机的内参矩阵，F为求得的基础几张。然后通过SVD分解恢复出摄像机外参R和T，从而可以求得摄像机投影矩阵P。

通过上面步骤得到了匹配点的坐标和相机投影矩阵P。在对极几何约束下一对匹配点反投影射线在空间中相交，该空间点位置坐标即为两匹配点对应的三维空间点。故对于需要重建的两张图像：

假设空间点X（X,Y,Z,1）T在图像上的投影为图像点 x（x,y,1）T，则有：

进一步得到:

其中,PiT是矩阵P的第i行。因此通过两图可以得到：

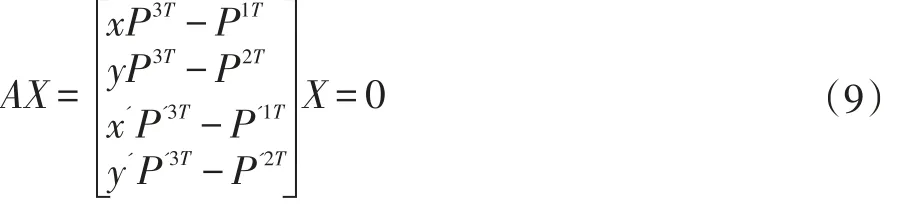
这是一个具有四个齐次未知量的四个方程,其解在相差一个尺度因子下被确定。对矩阵A采用SVD可求出对应三维空间点的坐标X（X,Y,Z,1）T。

采用上述三维重建方法，依次对相邻两张图像进行重建，可以得到初始三维重建结果：稀疏的三维点云。且传统的方法对于加入的待重建的图像，会将它和所有已加入的图像进行尝试重建，这也会在很大程度上增加重建时间。

1.3点云优化

每次加入图片会重建出三维点，得到的只是初始的三维点，需要在每次加入图片重建出三维点后对已有的点云进行优化。对于重建出的点云理论上满足：

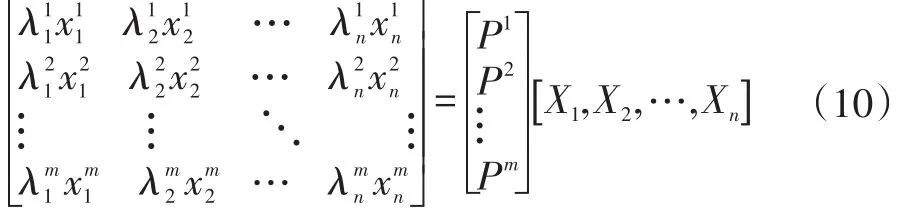
其中Xj代表空间中第j个三维点，Pi代表第i个相机，xi

j表示第j个3D点经过第i个相机在图像上的投影。优化目标就是：

其中d（x,y）代表齐次点x和y的几何图像距离，i是优化估计后的投影矩阵，j是优化估计后的3D点，表示第j个3D点经过第i个相机在图像上的投影。在每次加入图片重建后，都需要进行一次全局优化，然后将反投影误差较大的点剔除，直到去除所有的异常点后继续加入下一张图片进行重建。所有图片都加入重建完成后，再进行一次整体优化。重复上述去除异常点步骤，得到重建后稀疏点云。然后将稀疏点云文件输入PMVS2中，通过特征匹配、扩展和过滤过程将稀疏点云稠密化，得到最终的三维点云模型。

2 实验结果与分析

硬件环境基于Intel Core i7-4790k CPU@4.0 GHz。本文实验使用了22张图像的数据集，分别用文献[12]中提供的方法和本文的方法，比较结果如图1所示。

在时间花费上，文献[12]中的方法稀疏重构部分共计花费895s,本文的方法共计花费208s，其中主要的差别体现在图像匹配部分，文献[12]中的方法和本文方法耗时分别为828s和194s。在增量重建部分本文方法也比文献[12]中方法要快一点，但差距并不明显。总体来说，本文在时间花费上比文献[12]中方法具有比较明显优势，且由分析可知，输入图像的数量N越大，优势会越明显。

实验结果表明，与传统的多视角三维重建相比，本方法能达到相同水平的重建效果，甚至在某些局部区域具有更好的结果，且在时间上更具有优势。但由于本算法要求输入图像序列有序，因此对数据采集要求较为严格，无法处理无序图片序列。故本算法仍需改进，需要做到能对无序图片筛选排序。

图1 [12]中的方法和本文方法进行比较

[1]Horn B K P.Shape from Shading:A Method for Obtaining the Shape of a Smooth Opaque Object from One View[J]，1970.

[2]Bakshi S,Yang Y H.Shape from Shading for Non-Lambertian Surfaces[C].Image Processing,1994.Proceedings.ICIP-94.,IEEE International Conference.IEEE,1994,2:130-134.

[3]Subbarao M,Gurumoorthy N.Depth Recovery from Blurred Edges[C].Computer Vision and Pattern Recognition,1988.Proceedings CVPR′88.,Computer Society Conference on.IEEE,1988:498-503.

[4]Clerc M,Mallat S.The Texture Gradient Equation for Recovering Shape from Texture[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24（4）:536-549.

[5]Loh A M,Hartley R I.Shape from Non-Homogeneous,Non-Stationary,Anisotropic,Perspective Texture[C].BMVC.2005:69-78.

[6]Massot C,Hérault J.Model of Frequency Analysis in the Visual Cortex and the Shape from Texture Problem[J].International Journal of Computer Vision,2008,76（2）:165-182.

[7]Favaro P,Soatto S.A Geometric Approach to Shape from Defocus[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27（3）:406-417.

[8]Casas J R,Salvador J.Image-Based Multi-View Scene Analysis Using′Conexels′[C].Proceedings of the HCSNet Workshop on Use of Vision in Human-Computer Interaction-Volume 56.Australian Computer Society,Inc.,2006:19-28.

[9]Tomasi C,Kanade T.Shape and Motion from Image Streams under Orthography:a Factorization Method[J].International Journal of Computer Vision,1992,9（2）:137-154.

[10]Noakes L,Kozera R.Nonlinearities and Noise Reduction in 3-Source Photometric Stereo[J].Journal of Mathematical Imaging and Vision,2003,18（2）:119-127.

[11]Stewart C V,Dyer C R.The Trinocular General Support Algorithm:A Three-Camera Stereo Algorithm for Overcoming Binocular Matching Errors[C].Computer Vision.,Second International Conference on.IEEE,1988:134-138.

[12]Snavely N,Seitz S M,Szeliski R.Modeling the World from Internet Photo Collections[J].International Journal of Computer Vision,2008,80（2）:189-210.

[13]Lowe D G.Distinctive Image Features from Scale-Invariant Keypoints[J].International journal of computer vision,2004,60（2）:91-110.