基于模糊预测控制的城轨列车自动驾驶

何坤，肖壮，朱宇清，毛畅海

（西南交通大学电气工程学院，成都 610097)

0 引言

近年来，城市轨道交通的发展对于缓解城市快速膨胀的人口压力和日益严重的交通堵塞问题等方面发挥着越来越重要的作用。列车自动驾驶系统ATO的运用对于城轨列车的安全运行、准点精确停车、降低能耗等方面发挥着重要的作用。

既有的列车自动驾驶技术，一般以全程巡航模式进行速度跟踪控制，巡航的目标速度可依据时刻表进行计算[1]，这种方法实现简单，计算量小，可在限速约束下实现列车的正点运行。但是，实际的城市轨道线路往往存在较多的上下坡道，最大坡度可达±30‰[2]，若仍采用巡航控制，一方面会使得牵引和制动之间切换频繁，舒适性往往很难保证，另一方面由于缺乏必要的惰行工况，列车运行的节能性较差。采用模糊预测控制，成为协调工况切换平缓，保证速度跟踪性和节能性等性能间冲突的有效解决方法[3]。

文献[4]将列车节能运行优化和平稳舒适控制进行分层考虑，提出了一种基于两层结构的列车自动驾驶控制架构。顶层为基于节能的全局速度曲线规划器，底层为速度跟踪控制器，前者实现基于安全、正点约束的节能优化，后者以前者得到的优化速度曲线为参考进行跟踪控制，实现速度跟随，并确保乘客舒适性和停车精确性。

本文参考文献[4]的研究思路，在文献[5]基础上，将列车惰行节能优化曲线作为速度跟踪控制的输入，提出了一种基于惰行节能的城轨列车多目标预测控制方法。

1 模糊预测控制理论

作为一种非线性的智能控制理论，模糊控制对于系统模型建立的精确性要求不高，它基于人类专家的控制经验，运用模糊推理的方法实现系统的控制。针对类似于列车运行控制等一些较为复杂的非线性控制对象，模糊控制算法体现出其控制性能高，系统鲁棒性强的优点[6]。

预测式模糊控制的控制规则一般采用“IF-THEN”的形式，如式（1）所示，可解释为：若对当前系统施加了一个控制Ci若干时间后，可令系统的评价指标x为Ai，y为Bi，那么就将Ci输出给控制对象[6]。

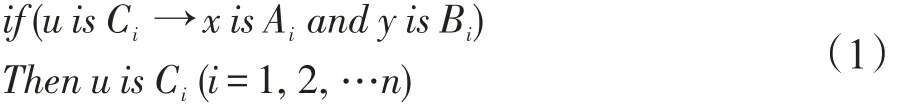
2 模糊隶属度函数

在模糊控制理论中，可通过定义隶属度函数去定量地表达一个模糊化的概念。考虑到列车在实际运行过程中需要达到的控制要求，本文分别对如下六个控制目标建立相应的隶属度函数，即 S、T、P、A、C、E，分别代表安全性（Safety）、追踪性（Traceability）、准点性（Punctuality）、停车精确性（Accuracy）、乘坐舒适性（Comfortability）、节能性（Energy Consumption）[7]。

对于控制目标S、T、P、A选取了高斯型隶属度函数，函数表达式如下：

2.1 安全性（S）

安全性作为城轨列车运行过程中最基本的准则，其他的一切优化目标都必须建立在行车安全的基础上。本文将列车的实际运行速度与该路段的安全限速值进行比较，从而衡量列车运行的安全性指标。例如，有一段安全限速值为65km/h的运行区段，速度的安全裕量为5km/h，若列车的实际运行速度与安全限速值有5km/h的裕量，则称“安全性好（SG）”，否则称“安全性差（SB）”。对应的安全性隶属度函数和图形如下：

其中VP（NP）是级位为NP时列车的速度，Vs为列车的安全限速值，Verror为速度的安全裕量值。

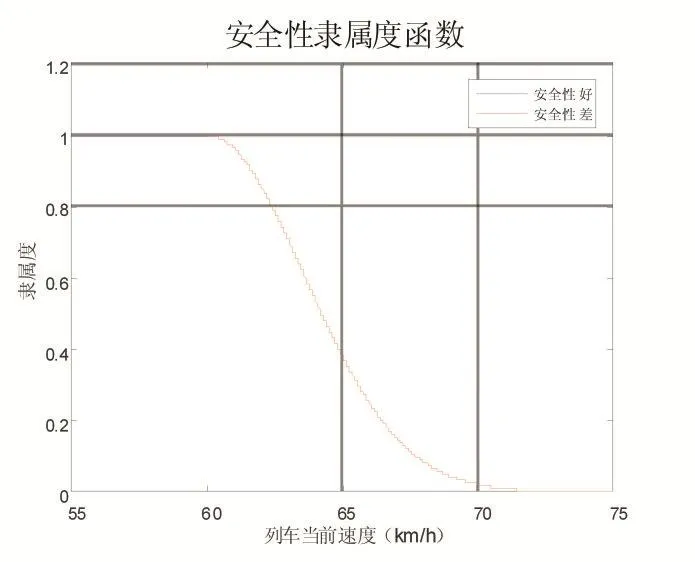
图1 安全性隶属度函数

2.2 追踪性（T）

将生成的优化节能运行曲线作为列车自动驾驶的目标跟踪曲线，通过对比列车在施加了不同控制级位后的下一步长的预测速度与目标速度的对比情况，评价列车追踪性能的好坏。本文仿真案例中，若假设列车运行的目标速度为60km/h，速度允许最大误差范围为±2km/h，如果列车的实际运行速度正好等于目标速度，则称“追踪性很好（TVG）”。如果实际运行速度与目标速度的差值在最大允许误差±2km/h范围内，则称“追踪性好（TG）”，否则如果偏差较大，则称“追踪性差（TB）”。则追踪性的隶属度函数和图形如下：

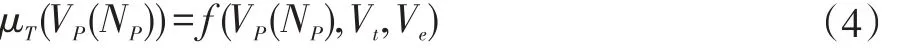
其中，VP（NP）是级位为NP时的列车速度，Vt=Vtarget是列车运行的目标速度，Ve=Verror是列车的目标速度与实际走行速度的最大允许误差。

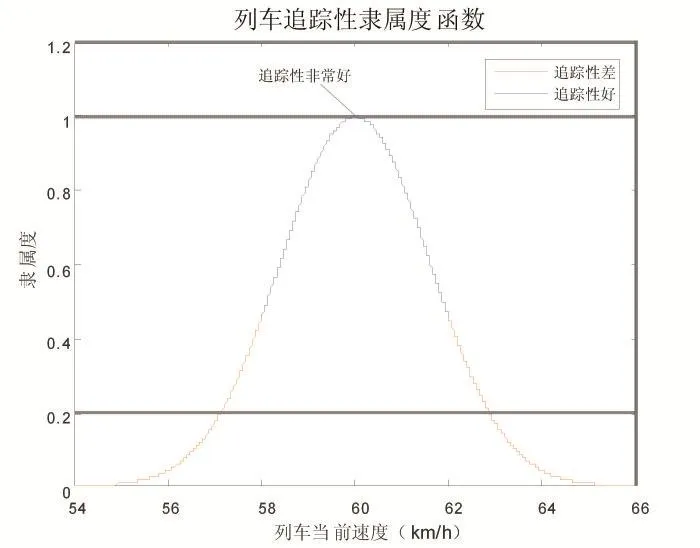
图2 追踪性隶属度函数

2.3 准点性（P）

对于城轨列车来说，准点性也是十分重要的一项评价指标。由于地铁列车的运行区间较短，故运行时间的合理误差通常在几秒到十几秒的范围内。设列车正点运行时间为243s，若规定列车实际运行时间和正点运行时间的误差在±1s范围内，则称“准点性很好（PVG）”，若误差在±5s内，则称“准点性好（PG）”，否则称“准点性差（PB）”。则准点性的隶属度函数和图形如下：

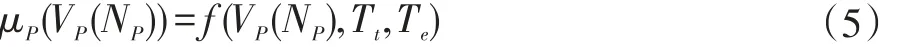
其中Tt=Ttarget为列车的正点运行时间，Te=Terror为城轨列车运行时间误差允许值，VP（NP）是级位为NP时的列车速度。

2.4 停车精确性（A）

对于地铁列车站点停车来说，因为许多站台都安装有安全屏蔽门等设施，故对于地铁列车的停车精确性有十分高的要求。如果列车的停车位置在目标停车位置的±5cm范围内，则“停车精确性很好（AVG）”，若停在了目标位置的±25cm范围内，则称“停车精确性好（AG）”，否则称“停车精确性差（AB）”。则相应的停车精确性隶属度函数表示如下：

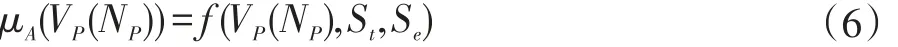
图3 准点性隶属度函数

其中，St=Starget为列车的目标停车位置，Se=Serror为城轨列车停车精度的误差允许值，VP（NP）是级位为NP时列车的速度。下图是精确停车位置为4120m对应的隶属度函数曲线：

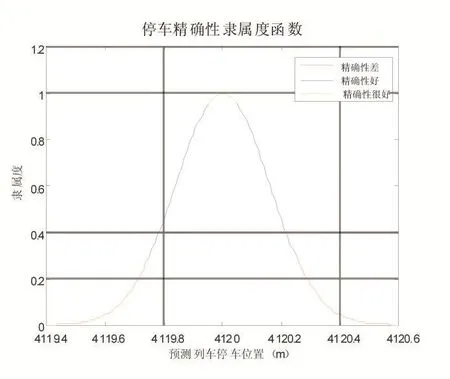
图4 停车精确性隶属度函数

2.5 乘坐舒适性（C）

旅客乘坐的舒适性可以从列车加速度的大小、加速度变化的频率和幅度来衡量。因此本文通过城轨列车的牵引或制动级位的变化情况来反映列车加速度的变化情况，从而衡量乘坐舒适性的性能指标。因此，本文以两次牵引或制动级位变动的间隔时间t和级位差Nchange作为衡量旅客乘坐舒适度的评价指标，若间隔时间长，级位差小，则称“舒适度好（CG）”，反之为“舒适度不好（CB）”。本文设定舒适性指标的隶属函数为式（7）：

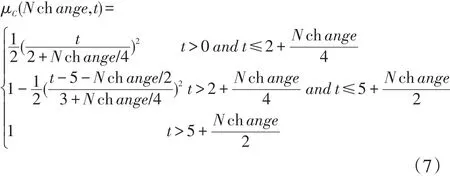
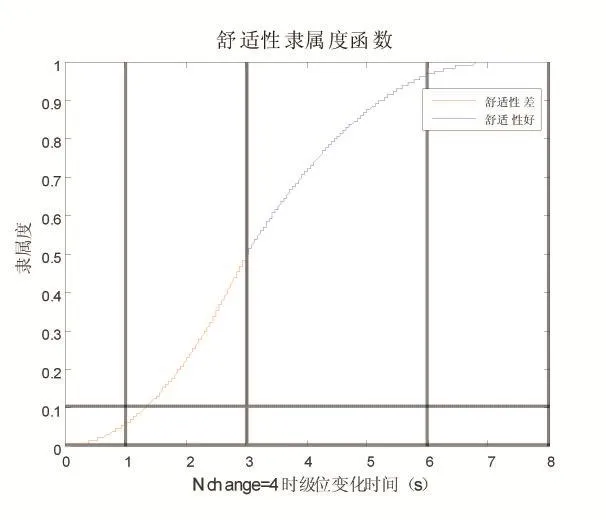
图5 乘坐舒适性隶属度函数

2.6 节能性（E）

列车在运行过程中，牵引能耗占列车总能耗的很大一部分，通过合理的惰行来消耗列车运行富裕时间，可以很好的达到降低能耗的作用。本文通过惰行优化节能算法对列车运行曲线进行优化处理，生成的最优运行速度曲线可作为ATO系统自动驾驶列车的参考目标曲线。只要通过模糊预测控制算法使列车的实际运行曲线较好的跟踪优化曲线，便能达到列车运行节能的目的。因此本文规定：在下一个步长范围内，若预测的最优级位N=0，即惰行，则“节能性好（EG）”，否则为“节能性差（EB）”。

3 列车人工驾驶策略

优秀的列车司机在实际驾驶列车过程中，会综合考虑诸如安全性，准点性，乘车舒适性等指标，结合丰富的驾驶经验，适当的调整列车的牵引力和制动力，使列车平稳、有效的运行。

将优秀司机的操纵经验总结成列车操纵的三大人工控制策略：恒速运行控制阶段（CSC），目标速度为设定恒速的阶段；自动停车控制阶段（TASC），通过调节列车的速度使其停靠在指定的目标位置处；惰行节能准点控制阶段（CC），通过将列车实际运行时间与准点运行时间相比较，控制列车进入惰行工况的时间，进入惰行工况后，列车保持惰行直至惰行阶段结束，以此达到降低能耗的目的。

3.1 定速巡航控制（CSC）

列车从起车到匀速运行的过程中，以乘车舒适性与追踪性为主要控制目标，逐级的增大牵引级位，使列车能按照已知的优化曲线平稳、快速的到达恒速运行。如果在列车的运行前方有低限速区段，列车将在通过该限速点之前达到目标速度，避免超速。列车人工驾驶的恒速控制阶段操纵经验如下：

CSC-1如果列车的运行速度超过安全限速，则采用最大能力制动。

CSC-2如果列车运行的速度远低于线路的限速，则需适当增加牵引级位。

CSC-3如果列车保持当前的牵引级位会使得列车的实际速度与目标速度的偏差过大，则应该在适当范围内改变牵引或制动级位，使实际运行速度能更好的追踪目标优化速度，同时级位变化的频率也应当适当考虑。

CSC-4如果列车的实际运行速度在事先确定的允许速度范围内，则控制级位保持不变。

3.2 自动停车控制（TASC）

在列车接近停车点之前的某段距离，设置有表示列车距离前方目标停车位置距离的列车自动停车位置光标B。司机将会根据对光标B的观测来实现对列车的停车控制，在此过程中将主要考虑停车的精度和乘坐的舒适度。列车人工驾驶的自动停车控制阶段操纵经验如下：

TASC-1：列车运行在TASC区域内，若使列车保持当前的控制级位不变，列车可以很好的停靠在预先设定的停车允许误差范围内，则控制级位保持不变。

TASC-2：在列车靠近TASC区域时，先施加轻微的制动，使列车缓慢减速，然后再逐级增大制动，以减小对旅客乘坐舒适性的影响。

TASC-3：在TASC区域运行，若列车以当前的级位会使列车停车位置不当，则需要在一定的范围内变化制动级位以使列车正确停车，同时要注意换挡之间的时间间隔，以保证乘坐舒适性。

3.3 惰行节能准点控制（CC）

本文基于由惰行优化算法生成的节能优化曲线，通过模糊预测控制算法实现列车的自动驾驶功能。惰行运行区段可使列车减少因制动而导致的列车动能的损失，降低列车的运行能耗，因此，列车人工驾驶的惰行控制阶段的操纵经验如下：

CC-1：根据优化目标曲线，列车在进入惰行起始点前一段距离的位置时，如果列车实际运行时间与优化曲线的准点时间相比，在没有晚点的情况下有多余的富裕时间可以利用，则可以在进入惰行工况转换点前就开始实施惰行，以达到进一步节能的目的。

CC-2：若在列车进入惰行起始点前一段距离的位置时，判断列车出现晚点的情况，可以适当推迟惰行起始点的位置，同时提前制动的起始点，使惰行的距离变短，从而在保证节能的情况下能使列车的晚点时间得到补偿，达到准点运行的目的。

3.4 模糊预测控制规则

根据上文关于列车的人工操作策略的总结，可以将优秀司机的人工驾驶策略转化成模糊预测控制规则，如下所示，其中控制量都是离散的，牵引级位为Pn，制动级位为Bn，n的范围为1～7。其中，P7是最大能力牵引，B7是最大能力制动，Dn是牵引或者制动的级位差。

（2）自动停车控制规则

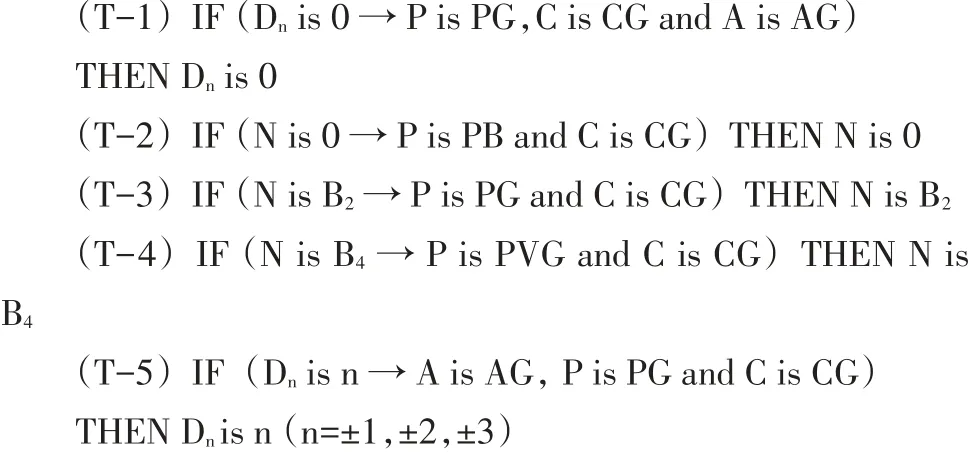
（3）惰行节能准点控制规则

在列车进入惰行起始点前一段距离的位置处：

4 实例仿真验算

为了验证此模糊预测控制算法的正确性和可行性，本文选取了具体的列车参数和线路进行仿真模拟。

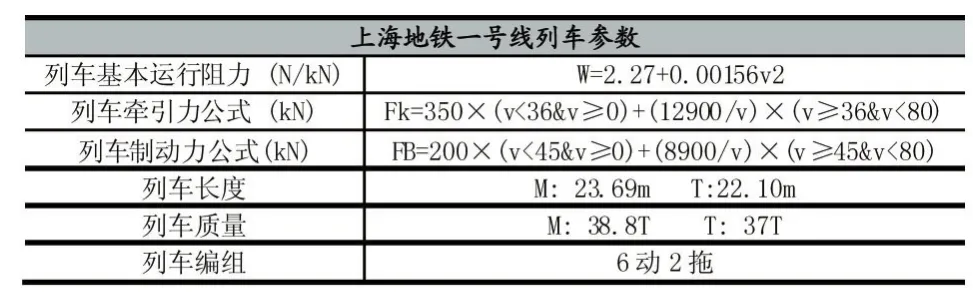
表1 列车参数

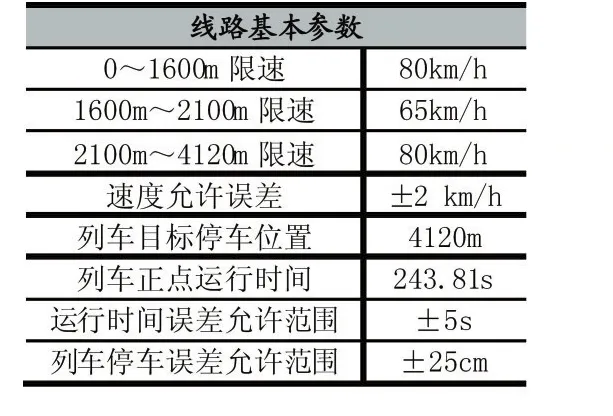
表2 线路数据

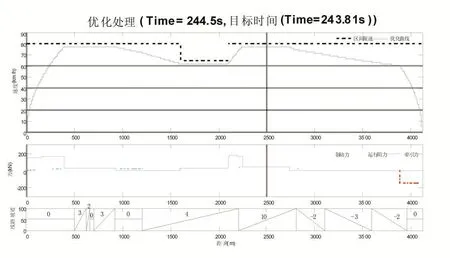
图7 节能优化运行曲线

如图6所示，仿真系统运行时，根据图7中生成的惰行节能优化曲线，首先读取此优化运行曲线的速度值，然后通过施加不同的牵引力或制动力，计算6个控制目标的隶属度函数值，从而求得最优的控制级位，并将该级位实际输出给列车，以此实现滚动优化这一过程直到列车进站停车，最终达到列车自动驾驶的目的。

图8 最优运行曲线与跟踪曲线

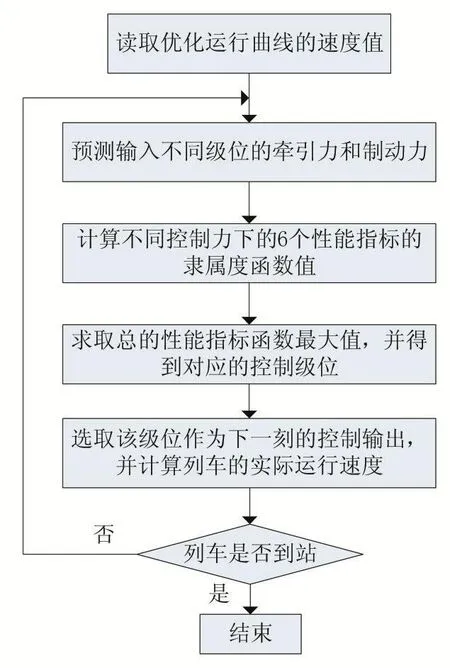
图6 模糊预测控制算法实现流程

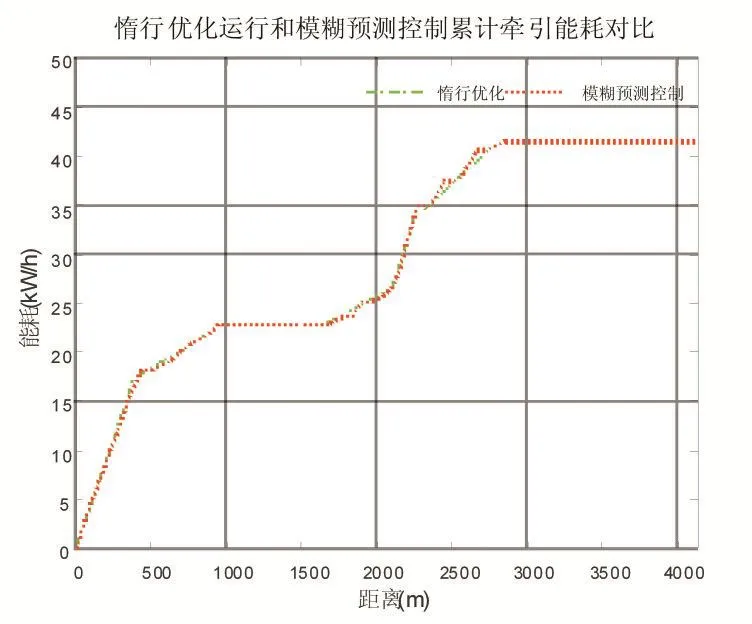
图9 惰行优化和模糊预测控制的能耗对比

表3 仿真数据结果

仿真结果如图7-9和表3所示。由图8可得，红色为列车的优化速度曲线，蓝色为列车实际的跟踪曲线，两条曲线很接近，并且在整个区间运行过程中，列车的速度都没有超过限速。因此列车运行的追踪性与安全性都是满足要求的。

另外，列车的实际停车位置为4120.18m，在允许的停车位置最大允许误差25cm的范围内，因此列车的停车精确性性能较好。从列车实际运行的速度-距离曲线可以看出，列车速度基本是按照一条比较平滑的曲线变化的，此外从级位的变化图中也可以看出所有的级位的变化都不是过大或者过快，变化相对比较平缓，除了接近停车点前，列车频繁地切换制动级位以达到精确停车的目的。因此旅客乘坐的舒适性指标也达到了基本要求。

对城轨列车而言，准点性是十分重要的一项性能指标。从表3可知，跟踪曲线下列车的实际运行时间为245.07s，相比于正点运行时间243.81s，准点性满足要求。另外列车实际运行能耗为41.40kW/h，相比于优化运行曲线的能耗40.611 kW/h，跟踪控制过程的节能性较好。

5 结语

本文以基于惰行控制的节能优化算法生成的列车运行优化曲线为跟踪目标，采用模糊预测控制算法，对不同的列车控制目标建立了模糊隶属度函数，总结了优秀司机的人工驾驶策略，并得到了相应的模糊控制规则。以城轨列车具体的仿真参数和线路进行模拟，能在满足准点、精确停车等控制目标的情况下有效跟踪目标曲线，验证了多目标模糊预测控制算法的正确性和可行性。

[1]林颖.基于在线计算方式的车载ATO运行模式曲线优化模型研究[D].成都：西南交通大学,2013.

[2]黄舰.城市轨道列车节能优化控制研究[D].成都：西南交通大学,2015.

[3]Seiji Y,Shoji M.Automatic Train Operation System By Predictive Fuzzy Control[J].Elsevier Science Publishers B.V.（North-Holland）,1985.

[4]Wang Q Y,Wu P,Liang Z C,et al.The Hierarchical Real-Time Control of High Speed Trains for Automatic Train Operation.In:Computers in RailwaysⅪⅤ.WIT Press,2014：17-36.

[5]黄舰,曲健伟.地铁列车基于惰行控制的节能优化运行研究[J].机车电传动,2015（3）:69-73.

[6]单冬.模糊控制原理与应用[M].北京：中国铁道出版社,1995.

[7]Hiroyasu O,Seiji Y,Shin-ichi S.Automatic Train Operation System Based on Predictive Fuzzy Control[J].International Workshop on Artificial Intelligence for Industrial Applications,1988.