基于改进的粒子群优化算法的SDN负载均衡研究

李瑞玲，易向阳

（广西大学计算机与电子信息学院，南宁 530004）

0 引言

在面对复杂网络流量和新兴的网络业务时，以TCP/IP为核心的传统网络框架表现得越来越难以维护和扩展，并且传统的网络框架无法为研究者提供特定环境下各种技术和新功能的相关支持，这些相关问题严重限制了互联网的行业发展前景，也促使人们对新的网络架构进行研究。因此，数据中心网络应运而生，数据中心网络是一个连接数十万乃至百万级的大规模服务器群，作为连接分布式存储和计算的桥梁，数据中心的性能将直接影响云计算、大数据等业务的发展。因此，如何对流量进行有效的控制，保证网络的利用率，实现有效的负载均衡，节约网络的资源，成为数据中心网络研究中需要解决的核心问题之一。

为了更好的解决数据网络中负载均衡问题，同时也为了灵活方便的对其进行规划以及对设备进行有效的管理，研究者提出了软件定义网络（Software Defined Network，SDN）这一概念[1]。SDN相较于传统网络的不同之处在于其运用了分层的思想，将数据层与控制层分隔开，从而实现了对网络流量的灵活有效控制。在控制层面，涵盖了有逻辑的中心化与可编程特点的控制器，通过控制器可控制了解全局网络的信息，也方便了运营商和研究者对网络的配置以及新协议的部署等；而在数据层面的交换机仅仅提供一些简易的数据转发功能，这样就大大提升了对网络匹配的数据包的处理速度，同时也解决了对庞大流量的需求问题。

针对传统网络存在的众多弊端，SDN的出现为解决这些弊端提供了新的思路。例如，基于SDN技术的数据中心有很多优点[2]。首先，基于SDN网络管理与控制相分隔的特点，运营商和研究者可以通过控制器掌握全局的网络信息，随时查看网络的负载情况。其次，通过负载均衡算法优化网络的链路负载情况，不仅提升了SDN网络的性能，也极大地降低了运营的成本。最后，对于引进的新的网络及应用，SDN只需在控制层面加入相应的策略算法，无需再对底层的硬件进行更换，不但节约设备成本，也解决了传统网络难维护和扩展差的问题。

另一方面，在数据中心需要处理庞大的网络数据流量时，对链路的负载均衡提出了更为严格的要求，而基于SDN的负载均衡的相关技术在一定程度上为该问题提供解决思路。本文设计并改进了一种多商品流的粒子群优化（Particle Swarm Optimization,PSO）算法并用于求解负载均衡问题。针对求解过程中PSO算法在搜索后期易陷入局部最优的困境，本文在构建了基于路径长度与链路利用率的大象流分布的算法目标函数的基础上，提出了改进的粒子群优化（Improved Particle Swarm Optimization,IPSO）算法，该算法结合分治算法的思想，将整个粒子群体划分成多个子群体，然后对这些子群体分别求得各自的全局最优解，最后再对所有的子群体的全局最优解进行加权平均，最终求得整个粒子群体全局的最优解。

本文首先介绍当前数据中心的广泛使用，接着引出SDN环境下实现数据中心的负载均衡的研究情况；然后根据众学者对负载均衡以及PSO算法不断的研究改进和完善的基础上，给出负载均衡优化的模型，并提出一种改进后的IPSO优化算法，基于该算法给出一种SDN负载均衡方案；最后对算法进行控制仿真验证，并对全文作出总结。

1 相关研究工作

近年来，随着对SDN技术不断的研究，众多学者尝试着将SDN应用到数据中心中，利用SDN集中控制的这一优点来改善现有的流量管理方式，对链路产生的流量选用负载均衡算法来进行相关调度。目前，常见的流量调度负载均衡算法包括等价多路径（Equal-Cost Multi-path Routing，ECMP）算法、Floodlight自带的单路径最优路径算法、包轮询算法以及粒子群优化负载均衡算法等。Gao等作者在文献[3]中详述了ECMP算法，该算法适合处理链路中的老鼠流问题，在处理大象流问题时，链路的流量容易分配不均从而会导致网络的传输的性能下降。文献[4]中针对大象流使用EC⁃MP算法进行测试，结果证明传输性能下降达50%；文献[5]中提到了包轮询算法，该算法可以确保每条路径上的转发包数基本相同，但是即使是文献[6]中改进后的差额轮询算法也无法避免数据包乱序到达从而产生的链路拥塞问题。

PSO算法[9]是受到鸟群觅食的行为启发而发现的一种群体的智能优化的算法，是由James Kennedy和Russell Eberhart博士在1995年提出的。该算法从随机解开始，多次迭代去找寻满足条件的最优的解，再根据适应值来判断找到的解的优劣。文献[9]中给出了一种基于多商品流的PSO负载均衡算法，这种算法以其实现容易、精度高、收敛快等优点，很好地契合了求解多商品流的问题，从而能高效快速的找到符合链路的最优路径，使得链路的负载趋于平衡。但是PSO算法也存在着一些问题，比如算法搜索后期的收敛性变差、寻优的精度变低以及容易陷入局部最优解等。为了改进算法，文献[11]中提到了自适应的调整惯性因子的策略，这样算法不但在前期就有较大的搜索能力，而且在搜索后期也能较为精确；文献[12]中给出了一种带收敛因子的PSO算法，与PSO算法相比较，经实验测试表明，改进后的算法的收敛性更好；文献[13]中提出了通过选用不同邻域的拓扑来确保收敛PSO算法的性能，结果表明，改进后的算法较PSO算法的全局拓扑性能更好；文献[14]中提到了一种动态邻域的PSO优化算法，并且将这种优化算法运用到了求解多个目标优化的问题当中；文献[15]将人工蜂群算法和PSO算法相结合，再通过基准函数的仿真，实验证明了改进后的算法性能更佳。

基于上述分析，以及众学者对PSO算法不断的改进与完善的基础上，针对PSO算法搜索后期易于陷入局部的最优的这一缺点，本文在文献[9]的基础上改进了PSO算法，并结合分治算法的思想，对粒子群体进行全局的最优处理，以便得到全局的最优解，最终解决链路的负载均衡问题。

2 改进的IPSO算法及负载均衡求解

2.1 多商品流及PSO算法描述

在SDN网络当中，我们把流量分为两种[7]，一种是长时间的稳定的流，称之为大象流，另一种是短时间的不稳定的流，称之为老鼠流。针对这两种不同的流采用不同的负载均衡方案，由于老鼠流持续时间很短，对链路影响不是很大，因此针对这种流可以采用ECMP算法进行转发，而本文的负载均衡方案主要是针对稳定的大象流。

多商品流问题是指在同一时间内通过寻找不同的路径，将种类不同的商品从各源点分送到相应的目的节点，在符合相应约束性条件的前提下，使得产生的花费最少[8]。在文献[8]中，Ghamisi等作者详细介绍了多商品流问题，阐述了将多商品流方法应用到网络流量调度问题上的可行性和优势。根据描述，可以把商品流中的商品文本看成是稳定流中的带宽请求，同时设定一些相应的约束条件，如设定网络中可以传输的流的最大数量为K，转换成商品流问题后，目标就成了在相应约束条件下，从整个网络中寻找不同的满足要求的路径，将流量发送到相应的目的节点，同时确保网络产生的开销最小，提高网络的链路利用率。本文中，结合商品流问题可以将数据中心的流量调度问题做如下的描述：

将网络 G 描述为（V,E）的集合（即 G=（V,E）），其中V表示所有节点的集合，E表示所有边的集合，设定e（i,j）为起点 i到终点 j的边，用 bi,j表示边 e（i,j）链路的带宽。设定有K条流在G中传输，设定流k（1≤i≤K）需求的带宽为dk，xijk表示 k个流在边 e（i,j）上的流量，xk表示为流量的矢量，ck表示流k的单位流量中的传送代价的矢量，这样就可以将目标函数表示为：

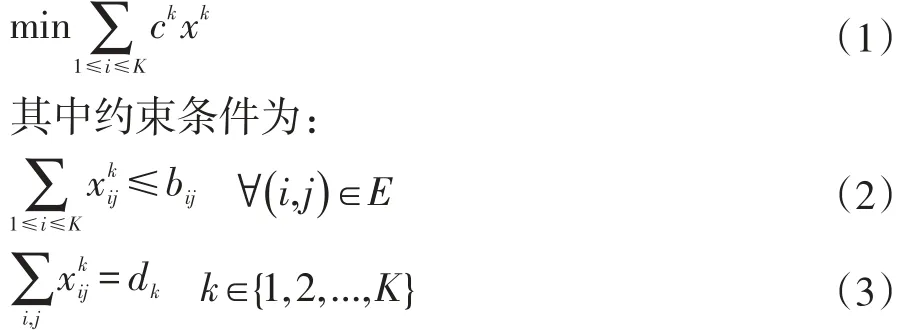
即在符合（2）式链路的带宽以及（3）式流量的请求的带宽约束的条件下，让整个网络的传送代价达到最少。

定义P为所有的路径的集合，则pi表示为从源节点到目的节点的可行性的路径上的第i条路径，其中，每一条路径都是有许多条链路e（i,j）构成的，采用线性函数可以将权值作如下定义：

其中a，b为常量，phl为 pi的长度，pul为 pi的利用率。

在将网络中的大象流调度问题转化为求解多商品流的问题时，要让大象流尽可能地先选择网络带宽剩余比较多的路径，也要尽可能的去躲避开链路中利用率比较高的路径，同时尽可能的躲避开与链路中其它的大象流发生碰撞。为满足上述各条件，通过改变权值ck可以控制网络的整个流量的分布情况。综上所述，在给定的网络G=（V,E）中，基于路径的长度与链路的利用率的大象流分布的算法的目标函数可表示为:

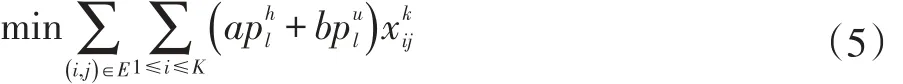
这样，（1）式中目标函数求解链路最小代价的问题就转化为（5）式中目标函数求解网络最低传输代价的问题了，即本文中所要解决的网络负载均衡问题。在将网络中大象流的调度问题转化成多商品流的问题后，先求解多商品流的问题，再根据求解结果确定转发的路径，这样不仅可以做到避免链路的拥塞，同时也提升了整个网络的利用率。由（2）式（3）式可知，在求解的过程中需要满足链路的带宽以及流量请求的带宽等约束条件，而PSO算法能够很好地解决约束优化问题，该算法易于实现，并且具有高精度、快速收敛等优点，很好地契合了求解多商品流的问题，基于此，本文采用了PSO算法来求解多商品流的问题。

PSO算法中，所有的粒子都会有一个被目标函数所确定的适应值（Fitness Value），通过这个适应值来评价粒子的“好”与“坏”。应用PSO算法来解决约束性的优化问题时有两个步骤较为重要，一个是对问题的解进行编码，另一个就是要确定好适应值的函数。例如给定一个问题f（x）=x12+x22+x32，要对其进行求解，则在用PSO算法求解时可将粒子编码为（x1，x2，x3），则f（x）就可表示为适应值的函数。基于此，可构造数据中心的大象流的调度问题的适应值函数如下所示。

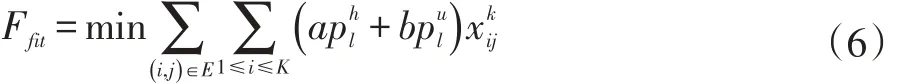
每个粒子的相对位置对应了问题的一个解，并且每个粒子在不断寻找自身的最优位置的同时也在寻找整个群体中最优粒子的一个位置。在整个的迭代过程中，为了改变自身的位置，使得自身离最优粒子的位置更近，粒子通过比较自身的两个“极值”[9]的适应值的优劣来更新自身位置。一个是本身粒子所找到的最优的解，这个解称之为个体极值，用pBest来表示；另一个极值是整个的群体目前能找到的最优的解，这个解称之为全局极值，用gBest来表示。粒子的速度和位置具体的更新方式如下：

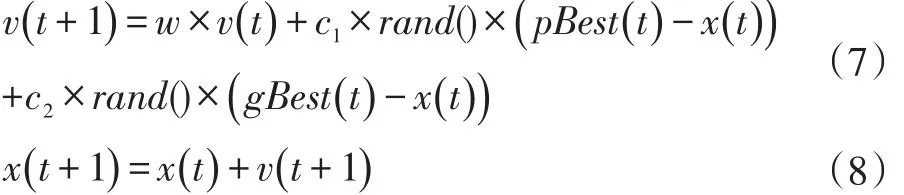
其中 t为迭代次数，v（t）表示粒子当前的速度，x（t）表示粒子当前的位置，c1、c2是学习因子，取值[0-2]的常数，w 是惯性加权因子，取值[0.1-0.9]的常数，rand（）是[0,1]随机数。

2.2 改进的IPSO算法及应用

文献[9]的基于多商品流的PSO优化算法能够很好的求得问题最优解，然而这些解存在着易于陷入局部最优的问题。PSO算法在查找的过程当中，群体中的所有粒子通过比较pBest和gBest的适应值来更新当前的位置，而粒子总是会往适应值好的粒子位置区域聚拢，这样就会出现粒子群体中的所有粒子都会往一个地方靠近，出现一种“聚拢”现象。随着聚拢现象的出现，算法就难以保证所求的解是满足条件的全局最优解。基于此，在PSO算法的基础上，本文提出了一种改进的粒子群优化算法。该算法结合分治算法的基本思想，将粒子群划分为m个子粒子群，并通过多次迭代的方式求得每个子粒子群的全局最优解，然后对这m个子粒子群的全局最优解进行均值求解，最后得到整个粒子群体的全局最优解。具体实现过程如下。

首先，将整个粒子群体划分为m个子群体，为达到子群体的最优效果，先选取其中一个子群体j，再对这个子群体的个体极值pBestj作如下的改进：在子群体j中取个体i（该个体极值为pBestji）的前后选取两个个体极值，分别记作 pBestji-1和pBestji+1

，根据下面的公式计算出i的个体极值，记作 pBest′ji。

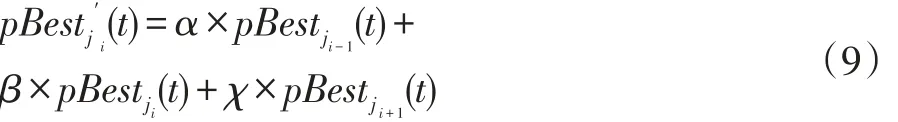
其中t为迭代次数，i表示第i个粒子，j表示第j个子群体,且 j∈（1,m），α、β、χ是[0,1]的随机数，满足α+β+χ=1。

对 pBestj的改进如下：将上面所有得到的子群体个体极值进行统计 pBest′j1、pBest′j2、...、pBest′jn，用这n个子个体的加权平均值表示pBest′j。

其中t为迭代次数，i表示第i个粒子，αi是[0,1]的随机的数，并且满足条件

选用上述方法，得到m个子群体的全局最优解后，再对这m个解进行加权平均值，得到最后的全局最优解 pBest′。

IPSO算法的流程图如图1所示。

图1 改进的IPSO算法流程图

算法IPSO While t＜=100 //满足迭代条件

2.3 算法性能分析

本文中改进后的IPSO算法，结合分治算法的思想，将粒子群体划分为m个子粒子群体，通过多次迭代的方式求得每个子粒子群体的的全局的最优的解，再对这m个子粒子群体的全局最优解进行均值求解得到整个粒子群全局最优解。这一方法很好的解决了PSO算法搜索后期易于求得局部的最优的解的问题。PSO算法的时间复杂度和迭代次数t以及维度n存在着线性的关系，时间复杂度为O（t*n），而IPSO算法是在PSO算法的基础上对整个群体进行划分的，因此，它的时间复杂度为O（mlogn）。同时在后续的仿真的实验中表明，该算法较PSO算法有更好的收敛效果，避免了PSO算法后期易于陷入局部的最优解的问题。

2.4 基于IPSO算法的SDN负载均衡方案

在SDN网络中，数据流进到网络中时，OpenFlow交换机开始解析该数据流，并与交换机中的流表开始进行匹配，匹配如果成功，开始执行流表里的相应操作（转发或丢弃）；如果不成功，交换机先将该数据流封装成消息，然后再传给集成了改进的IPSO算法的控制器中，通过IPSO算法来计算得出从源节点到目的节点之间的最优的路径，再通过流表下发的方式，告知交换机的数据流的转发方式，最后交换机根据流表的表项中的动作来对这些数据流进行转发，具体的实现过程方案如图2所示。

3 仿真结果与分析

为了对IPSO算法进行有效性验证，本文在Flood⁃light和Mininet的控制仿真环境下进行了实验[10]，整个实验是在Ubuntu14.04系统下进行的。在使用Mininet构建的拓扑网络中，选用iPerf软件来模拟了端到端的流量，iPerf软件是一个网络性能测试工具，能够创建指定带宽的数据流量，因此选用该软件对网络进行流量的灌输，并设定链路的带宽10Mb/s。算法中相关参数的描述和取值如表1所示。

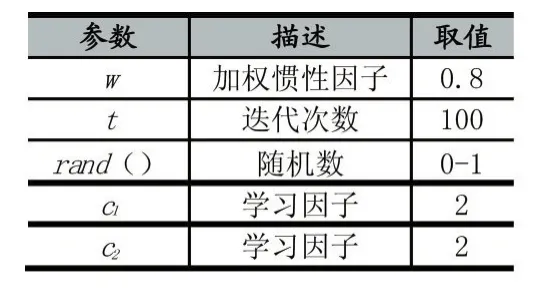
表1 仿真实验参数值

为了避免实验过程中出现的偶然情况，我们对自定义的网络针对不同的算法各做了六组实验，同时选取不同的链路来查看它们链路负载情况，本文主要是根据链路的延时以及链路的丢包率两方面来反应链路的情况，根据实验数据结果，绘制了图3和图4所示的曲线图。

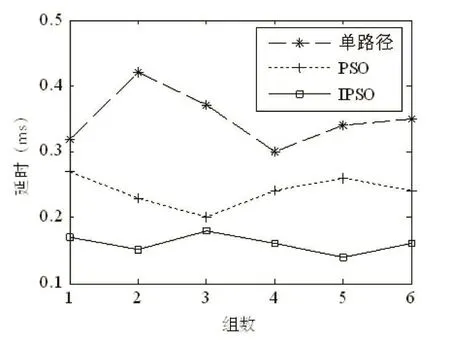
图3 三种算法的各链路延时

图4 三种算法的各链路丢包率

从上图3和图4中，我们能够很清楚地看出，无论是在链路延时还是链路丢包率的问题上，IPSO负载均衡算法相较于PSO算法和单路径算法在性能上都有着明显的提升，该算法较另外两种算法能够很好的保证网络链路的利用率，从而达到链路负载的均衡效果。而且在图中，我们能够看出IPSO负载均衡算法的曲线图走向相较于另外两种算法更趋于平稳，曲线波动范围较小，这说明IPSO算法在各组实验中都趋于平衡，稳定性较好，即改进后算法的可靠性更好。

随后，在基于Floodlight控制器的Dashboard网页界面上查看整体的网络的负载情况，图5、图6和图7是根据查看到的网络负载情况结果分别绘制出来的单路径、PSO和IPSO算法的效果图。

图中包含了交换机、主机以及它们之间的链路连线，其中不同的链路连线表示不同的链路利用率，细实线表示链路的利用率为0-0.3，虚线表示链路的利用率为0.3-0.5，点线表示链路的利用率为0.5-0.7，点虚线表示链路的利用率为0.7-1。

从上图中能够很清晰的看到，单路径最优选路算法出现了点虚线和点线的链路情况，说明这个时候链路利用率过高，出现了链路拥塞的情况；PSO算法虽然没有出现点虚线的链路，但也存在虚线和点线的链路情况，说明这个时候链路还是会有一些拥塞的情况出现，但不是很严重；而IPSO算法基本上都是细实线的链路，说明在采用IPSO算法后，链路都趋于平衡，没有出现链路拥塞的情况，同时也验证了该算法能够均衡网络中的流量，很好保证了链路的利用率。

4 结语

SDN具有集中管控、便于性能优化等优点，很好的解决了数据中心的负载均衡问题，而PSO算法能够很好的契合了多商品流问题，本文在众多学者研究的基础上，为更好的解决数据中心大象流负载均衡的问题，设计改进了一种基于多商品流的IPSO算法并用于求解负载均衡问题。该算法结合分治算法的思想，将粒子群体划分成多个子群体，并通过多次迭代的方式求得每个子群体的全局最优解，然后对这些子群体的全局最优解进行加权平均，从而求得整个粒子群体全局的最优解。最后，本文构建了基于Floodlight和Mini⁃net环境下的SDN数据中心实验平台，对单路径算法、PSO算法以及IPSO链算法的负载链路的均衡的策略进行了仿真实验比较，实验数据表明改进后的IPSO算法能够很好地对大象流进行可靠的传输，整个链路基本上趋于平衡且没有出现链路拥塞的状态，极大地确保了链路的利用率。

图5 单路径链路负载展示图

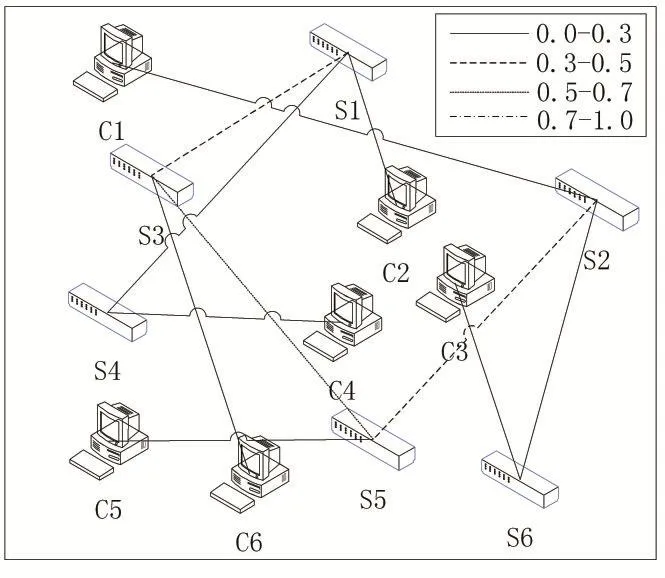
图6 PSO链路负载展示图

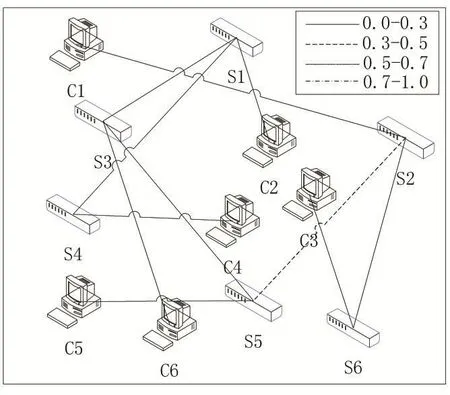
图7 IPSO链路负载展示图

[1]Wang Wen-Dong,Hu Yan-Nan.SDN:the ongoing Network Change[J].Journal of the technology,2013,19(1):39-43.

[2]Zhang Yuan.Based on OpenFlow Load Balancing Research[D].Beijing:Beijing University of Technology,2014.

[3]Gao Yan-Qing,Wang Hua.Research the Network Energy Model and Intelligent Algorithm Based on Multi-Commodity Flows[D].Shandong:Shandong University,2016.

[4]Al-Fares M,Radhakrishnan S,Raghavan B,et al.Hedera:Dynamic Flow Scheduling for Data Center Networks[C].Usenix Symposium on Networked Systems Design and Implementation,NSDI 2010,April 28-30,2010,San Jose,Ca,USA.DBLP,2010:281-296.

[5]M.Shreedhar,G.Varghese.Efficient Fair Queuing Using Deficit Round[C].SIGCOMM,1995:375-385.

[6]Liao Y.Adaptive Scheme on IEEE 802.11 PCF[J].Computer Science,2007,64(1):58-65.

[7]Mckeown N,Anderson T,Balakrishnan H,et al.OpenFlow:Enabling Innovation in Campus Networks[J].ACM Sigcomm Computer Communication Review,2008,38(2):69-74.

[8]Ghamisi P,Benediktsson J A.Feature Selection Based on Hybridization of Genetic Algorithm and Particle Swarm Optimization[J].IEEE Geoscience&Remote Sensing Letters,2014,12(2):309-313.

[9]Yu M,Rexford J,Freedman M J,et al.Scalable Flow-Based Networking with DIFANE[C].ACM SIGCOMM 2010 Conference on Applications,Technologies,Architectures,and Protocols for Computer Communications,New Delhi,India,August 30-September.DBLP,2010:351-362.

[10]Kreutz D,Ramos F M V,Esteves Verissimo P,et al.Software-Defined Networking:A Comprehensive Survey[J].Proceedings of the IEEE,2014,103(1):10-13.

[11]Shi Y,Eberhart R C.Parameter Selection in Particle Swarm Optimization[M].Evolutionary Programming VII.Springer Berlin Heidelberg,1998:591-600.

[12]Premalatha K,Natarajan A M.Hybrid PSO and GA for Global Maximization[J].Icsrs Int.j.open Problems Compt.math,2009,2(4):597-608.

[13]Specification,OpenFlow Switch.Version 1.0.0(Wire Protocol 0x01)[S].2009.

[14]Kreutz D,Ramos F M V,Esteves Verissimo P,et al.Software-Defined Networking:A Comprehensive Survey[J].Proceedings of the IEEE,2014,103(1):10-13.

[15]Jo E,Pan D,Liu J,et al.A Simulation and Emulation Study of SDN-Based Multipath Routing for Fat-Tree Data Center Networks[C].Simulation Conference.IEEE,2015:3072-3083.

[16]Kirkpatrick K.Software-Defined Networking[J].Communications of the Acm,2013,56(9):16-19.

[17]Wang Wen-Dong,Hu Yan-Nan.SDN:the ongoing Network Change[J].Journal of the Technology,2013,19(1):39-43.