常气压下非饱和土的一维瞬态渗流
李顺群,桂 超,夏锦红
新乡学院土木工程与建筑学院,河南新乡 453003
水在多孔介质中的渗流是岩土工程的基本问题之一. 土颗粒体几何形态和分布的复杂性和不确定性,是其微观流动表现为紊流而非层流的重要原因之一. 在渗流场内,所有运动要素不随时间变化而变化的渗流称为稳态流,否则为瞬态流. 另外,根据孔隙水充满孔隙的程度,渗流又可以分为饱和土中的渗流和非饱和土中的渗流[1-2]. 可见,岩土体在基质吸力作用下的吸水过程和失水过程属于非饱和瞬态流问题. 含水量和孔隙水的时空分布,对土的物理性质、渗透特点和力学指标具有深远影响. 当前,对入渗的研究主要集中在与降雨相关的诸多领域,包括液-气二相流[3-4]、污染物运移[5]、边坡稳定性研究[6]、地质灾害的力学机理[7-8]、非饱和渗流过程模拟[9-10]、水-力耦合[11-12]、以及蒸发时土的吸力变化等[13]. 在实验环境中,经常需要模拟土的失水这一自然过程. 如非饱和土的相关实验一般是从饱和状态开始并需要历经某一干燥过程,一般通过对试样施加气压力以使其失去一部分水的方法实现[14]. 由于非饱和土的土-水特征曲线存在明显的滞回效应,故常要求该干燥过程始终处于失水状态即避免任何时间段出现吸水[15]. 因此,研究气压力作用下,非饱和土中的水/气运动规律及瞬态渗流过程具有重要的理论意义和工程应用价值.
本研究基于Darcy定律,饱和度与基质吸力、渗透系数之间的经验关系,建立了非饱和三轴试样孔压消散的偏微分方程,并基于差分原理对该非线性偏微分方程进行了求解. 利用Wykeham Farrance(WF)非饱和土三轴实验系统进行了不同气压力作用下的非饱和土失水实验,利用差分方法得到了负孔压消散过程. 同时,利用有限元软件对这一过程进行了模拟. WF实验结果、非线性偏微分方程的数值解和有限元计算结果的比对表明,所建方程能够刻画非饱和土失水过程中的主要土力学和水力学特征.
1 土的一维失水过程
土体中大小不等的孔隙是相互连通的,这些孔隙常常可以理想化为一定尺寸的毛细管,如图1.
对某一特定地下水位A, 不同等效半径的毛细管中的液面上升高度是不同的. 通常情况下,较细毛细管中的液面高度h1高于较粗毛细管中的液面高度h2. 当进一步降低地下水位到B时,平衡后沿深度不同部位的毛细含水量会由于毛细高度的不变而进一步降低,处于A和B之间的孔隙水由饱和状态水变为毛细水. 相应的,毛细管中的液面也会降低为h3和h4.
实验采用轴平移技术可以模拟土的失水这一自然过程. 设想将试样的初始状态设定为饱和状态,在试样上部边界施加某一气压力,而将试样的下部边界通过高进气值陶土板和反压装置与外界大气相通. 由于上部边界气压力的存在,土中水会在压力差作用下由下部的高进气值陶土板流出. 随着时间的延续,非饱和范围及其饱和度都将发生变化. 一方面,非饱和区域从施加气压的一侧逐步向另一侧扩展,即毛细高度逐渐降低(图1中由h1到h3); 另一方面,随着水的排出,非饱和区域内不同位置处的饱和度也会逐步降低. 在此过程中,大孔隙中的水将首先被排出,即h2、h4始终低于h1、h3. 当施加的气压与孔隙水的表面张力作用平衡时,失水过程停止.
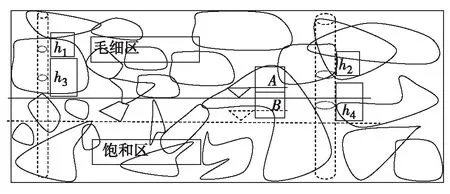
图1 孔隙体的毛细管模型及基质吸力作用Fig.1 The capillary model for pores in soil and the effect of matrix suction
高H的饱和土试样在气压p作用下排出一定量孔隙水后,获得非饱和土试样的过程如图2. 在图2中,圆柱体试样的初始状态是饱和的,其四周为橡胶模所封闭. 稳定气压p施加于试样上端,下端则通过高进气值陶土板与大气相通. 因此,在施加气压力的瞬时,气压力会全部作用于孔隙水上,试样的孔隙水压力等于所施加的气压力. 随后,孔隙水在压力作用下通过高进气值陶土板排出. 在排水过程中,试样的饱和度和渗透系数将持续减小.
流体压力包括孔隙水压力uw和孔隙气压力ua. 如果不允许排水,则饱和试样在施加气压p后,对应的孔隙水压力也是p. 排水阀打开后,孔隙水通过陶土板向下逐渐排出,孔隙水压力逐步消散. 当孔隙水不再通过陶土板排出时,说明孔隙水压力已经消散完毕,且与大气压平衡.
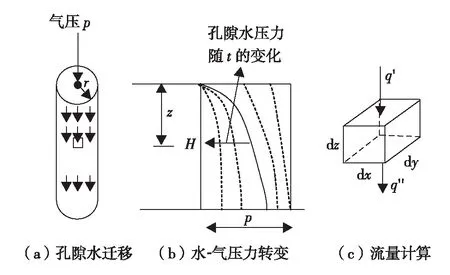
图2 非饱和试样施加气压力后的水气压力转换及流量计算Fig.2 The change of air and water pressure due to applied air pressure
实验采用重塑试样[16],土质为粉质黏土,其塑限和液限分别为17.4和28.0. 原状土经8 h烘干,过2 mm孔径筛后,配制成含水量(质量分数)为23%的湿土. 湿土密封保存24 h以上,待水气状态完全达到平衡后再进行制样. 重塑试样的制备采用击实法,试样为R70 mm×140 mm的圆柱体. 为了具有可比性[17],试样的干密度统一为1.70 g/cm3. 经计算,其湿密度为1.99 g/cm3,孔隙比为0.6. 湿土分3层装入击实仪中击实,每层的击实次数为30.
实验在WF应力路径三轴仪上完成,控制围压、反压、气压以及竖向压力,以实现不同实验目的对加载的需求. 首先,通过反压控制器对重塑试样进行反压饱和. 饱和阶段完成后,通过围压控制器对试样施加预定的围压并打开排水阀进行排水固结. 与常规饱和土的三轴实验相比,这里的反压饱和及固结排水并无太大区别. 接下来,在保持围压恒定不变的条件下,通过气压控制器经试样顶部施加气压力. 在气压力作用下,孔隙水通过试样底部的高进气值陶土板排出. 随着孔隙水的不断排出,试样由最初的饱和状态逐渐过度到非饱和状态,且这一过程从试样顶部开始逐渐向试样下部扩展.
压力施加与时间t的关系如图3. 对试样1施加的反压、围压和气压分别为0、150和100 kPa;对试样2施加的反压、围压和气压分别为0、400和200 kPa.
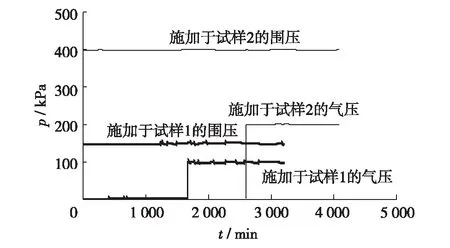
图3 围压和气压的施加过程Fig.3 The confining pressure and the air pressure applied on the samples
根据固结理论,固结度的计算可以基于变形,也可以基于孔压. 试样在某时刻的变形量除以最终变形量得到的固结度属于前者. 对于饱和土,基于变形的固结度还可以用某时刻的排水量除以稳定时总的排水量获得. 根据排水量获得的试样在两个阶段的固结度如图4,其中,曲线l1和l4分别表示试样1和试样2的固结度变化过程.

图4 围压和孔隙气压作用下的固结度变化Fig.4 The consolidation degrees in the saturated and the unsaturated stages
与饱和固结阶段的排水过程相比,施加气压力后的排水过程需要更长时间才能达到稳定,其原因在于非饱和土的渗透性远远低于对应饱和土的渗透性. 另外,在饱和排水阶段,较大围压作用下的排水过程需要较长时间才能达到稳定,这主要在于有较多孔隙水需要排出和土的孔隙比变化较大所致.
2 非饱和阶段的瞬态渗流模型
不管是饱和土的三轴实验,还是非饱和土的三轴实验,都是轴对称条件下的土力学实验,渗流过程都是沿着圆柱体轴线方向的一维流动. 为建立非饱和土三轴实验施加气压力后试样内部的水气平衡过程,有必要做如下理想化假设:① 土层是均质、各向同性和初始饱和的;② 土颗粒和孔隙水不可压缩;③ 排水仅在竖直方向发生;④ 气体在土中的渗透性远远大于水在土中的渗透性,且水的渗流服从达西定律;⑤ 在排水过程中,非饱和土的渗透系数可以表示为饱和土的渗透系数与饱和度的函数;⑥ 气压力一次骤然施加,在排水过程中保持不变;⑦ 排出的水量等于孔隙率与饱和度变化的乘积,即不考土颗粒体积的变化.
水的渗流只在孔隙的充水部分发生[18],即充水孔隙所占比重对渗透系数影响很大. 其原因主要有:① 孔隙中充水区域的缩小减少了过水面积;② 非饱和区域的存在必然导致绕流发生,从而增加水的流程;③ 水的流动越来越靠近土颗粒表面从而导致粘滞阻力加大. 因此,水在土中的渗透系数k随着饱和度的减小而急剧降低. 根据Brooks等的研究,非饱和土的渗透系数k可以表述为
k=kw,ua-uw≤(ua-uw)b
(1)
(2)
其中,kw、S=ua-uw、Sb=(ua-uw)b、se和δ分别为饱和状态时的渗透系数、基质吸力、进气值、有效饱和度和与孔隙尺寸分布指标有关的经验系数,且
(3)
(4)
对于细砂,λ=3.7; 对于粉质黏土,λ=1.8. 对于黏土,这里λ=1.0. 另外,基质吸力与饱和度之间的关系可以表述为
(5)
其中,λ是孔隙大小分布指标;s为饱和度;sr为剩余饱和度,表示基质吸力的增加不再引起饱和度显著变化时的饱和度. 因此,当ua-uw>(ua-uw)b时,有
(6)
在自然条件下,土的孔隙与大气相连,孔隙气压力等于大气压力. 所以,基质吸力由孔隙水压力决定,并最终与含水量存在某种对应关系.
在试样中取一个微元体,如图2所示. 则根据Darcy定律,进入该微元体的流量q′为
(7)
其中,i为水力梯度;A=dxdy;h为水头高度. 同样,流出微元体的流量q″为
(8)
所以,微元体孔隙水的流出量为
(9)
对于非饱和土,水压力为负,此时基质吸力与水头的关系可以表示为
S=ρwgh
(10)
故式(9)可演变为
(11)
与施加球应力围压相比,施加基质吸力引起的体变很小. 因此,可以不考虑基质吸力变化引起的体变. 所以,微元体内孔隙水的流出量还等于饱和度的改变量与孔隙率的乘积的相反数,即
dVw=-d(ns)=-nds
(12)
所以
(13)
根据式(4)、(5)和(10)可得
(14)
根据式(13)和式(14)可得
(15)
由式(11)和式(15)可得
(16)
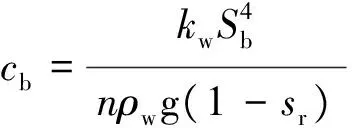
(17)
则式(16)为
(18)
其中,系数cb取决于土在饱和状态时的渗透系数,即孔隙状态、进气值、孔隙率和剩余饱和度等参数. 类似于饱和土Terzaghi一维固结理论中的固结系数cv,cb定义为非饱和土在一维气压力作用下的固结系数.
由于在实验过程中采用了轴平移技术,所以初始时刻和终止时刻的水压力条件为:① 当t=0, 0 另外,边界条件为:① 当0 式(18)是一个高度非线性偏微分方程,现有数值分析软件无法求解. 为此,本研究编制了专门求解该类非线性偏微分方程的程序. 由于是一维问题,所以只需考虑水压力沿三轴试样轴线方向z的变化. 沿z方向和时间t方向进行离散化,如图5所示. 其中时间步长为l, 轴线方向步长为m. 图5 非饱和三轴试样孔压变化的差分表示Fig.5 The difference method for the pore water pressure computation in the unsaturated triaxial samples 根据差分原理可以得到 (19) 类似可得 (20) 因此,式(18)的差分形式为 (21) 该差分方程与普通差分方程的显著差别在于孔压的3次幂的存在. 另外,式(21)可以简化为 (22) 其中, (23) 给定式(18)的初边值条件,可以得到初始值对应的u0(i, j+1), 将其代入式(23),可以求出k1、k2和k3. 之后根据式(22)可以求得对应的3个解. 其中与u0(i, j+1)最接近的那个解就是第2轮迭代时的u(i, j+1). 依此循环,直到前后两轮迭代结果的误差满足允许值为止,即得真实的孔压分布. 某时刻的孔隙水压力除以初始时刻的孔隙水压力可以得到该时刻的固结度. 图4中的l3和l6分别为试样1和试样2不同时刻的固结度曲线. 当前,针对三轴试验的数值模拟主要集中在本构模型方面[19]. 为了与前述实验结果和理论计算结果进行比对,本研究通过对Abaqus有限元进行二次开发,建立了饱和三轴试样施加气压力后,孔隙水压力消散的非饱和渗流过程有限元模型. 某时刻试样内的气压力分布如图6(a),在实验过程中,孔隙水压力设置为0. 所以,试样的基质吸力分布与气压力分布相同. 而在有限元模型中,一般不能施加气压力. 为了模拟非饱和土中的基质吸力,孔隙水压力可以设置为负值,如图6(b). 三轴试样是轴对称的,在建立模型时可以通过旋转二维平面模型得到圆柱体的方法予以实现,相关参数可以通过前述WF三轴试验得到,其弹性模量为7.5 MPa,泊松比为0.3. 渗透系数k与孔隙比e的关系可以通过不同围压时试样的渗透试验得到. 当孔隙比为0.55、0.60和0.67时,测得的渗透系数分别为4.8×10-9、1.0×10-8和6.7×10-8m/s. 图6 非饱和三轴试验与有限元模型的初边条件对比Fig.6 The comparison of the boundary and the initial conditions between the unsaturated triaxial experiment and the simulated model s与S之间的关系可通过Fredlund SWCC测试仪得到. 对于e=0.60的试样,当S分别为0、10、100、1×103、5×103、1×104、5×104、1×105、5×105和1×106Pa时,s分别为100%、91%、70%、58%、52%、49%、47%、45%、43%和41%. 如前所述,本模型主要有两个分析步,施加围压后饱和三轴试验的固结排水和围压不变条件下施加负孔隙水压力后的非饱和阶段排水. 在第1个分析步中,将模型中的孔压边界设为0,其余边界设为不透水边界. 在第2个分析步骤中,孔压边界设置为-50 kPa. 不同时刻试样中的流量对比如图7所示. 可见,与饱和阶段相比,非饱和阶段的流量分布存在明显差别. 施加气压后非饱和阶段的排水过程是由近及远、循序渐进的. 靠近排水边界的孔隙水首先排出,然后逐渐波及到试样内部的孔隙水. 图7 不同时刻试样中的相对流量对比Fig.7 The relative flows in the sample at different stages 某时刻的孔隙水压力除以初始时刻的孔隙水压力后可以得到该时刻基于孔压的固结度. 图4中的曲线l2和l5分别为试样1和试样2在不同时刻的固结度. 如前所述,图4分别给出了两个试样在饱和三轴固结阶段和施加常气压作用下排水固结两个阶段的固结过程. 其中,两个试样的实验成果如曲线l1和曲线l4所示;基于Abaqus有限元的计算结果为曲线l2和l5; 基于本研究非饱和土瞬态渗流模型的有限差分计算结果为曲线l3和l6. 可见,本研究给出的非线性偏微分模型充分反映了三轴试样在饱和状态三轴固结过程和常气压作用下瞬态渗流和孔压消散的主要特点,且基本位于实验结果和有限元计算结果之间. 因此可以说明,给出的非饱和土瞬态渗流模型是合理的. 3种方法存在差异的原因是多方面的,主要来源于模型的假设条件与实际情况存在一些差异. 比如均质、各向同性、初始饱和、达西定律、排水量等于孔隙率与饱和度的乘积等假设与事实均存在一定差异. 在实验过程中,即使施加气压能保持不变的假定也是难以完全达到的. 所以,实验值与本研究的非饱和土瞬态渗流模型计算结果存在差异是正常的. 图8 饱和、非饱和固结阶段试样不同部位的孔隙水压力Fig.8 The pore pressure distribution in samples in saturated and unsaturated consolidation stages 为了研究饱和阶段试样及非饱和阶段试样的孔压消散特点,图8给出了试样在饱和阶段固结和施加稳定气压条件下,孔隙水压力的变化过程. 其中,d为试样上各点与排水边界的距离. 由图8(a)可以看出,由围压引起的试样不同部位的孔隙水应力,在固结开始后的600 s左右基本消散完毕,且越靠近排水边界消散速度越快. 而图8(b)则显示,在施加稳定气压力后约75 000 s,水压力才基本消散完毕. 可见,非饱和土的固结过程比饱和土的固结过程慢得多. 产生这种现象的主要原因在于,随着水的排出,土的饱和度越来越低. 相应的过水通道越来越小,有效渗透系数也越来越小. 基于Darcy定律,饱和度与基质吸力、饱和度与渗透系数之间的经验公式,建立了三轴试样在受到常气压力作用后的负孔隙水压力消散偏微分方程,并基于有限差分原理建立了求解该高阶非线性偏微分方程的方法. 同时,利用Abaqus有限元软件对三轴实验常规固结阶段和气压力作用下的排水过程进行了模拟. 并将WF非饱和土三轴实验结果、偏微分方程数值解答和Abaqus有限元计算结果进行了比对. 结果显示,所建立的偏微分方程能够很好的刻画三轴试样在吸力作用下的排水过程. 引文:李顺群, 桂 超, 夏锦红. 常气压下非饱和土的一维瞬态渗流[J]. 深圳大学学报理工版,2018,35(1):70-77. / [1] LU N, LECAIN G D. Percolation induced heat transfer in deep unsaturated soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(11): 1040-1053. [2] FREDLUND D G, XING Anqing, HUANG Shangyan. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(3): 533-546. [3] ZHENG H, LIU D F, LEE C F, et al. A new formulation of Signorinip’s type for seepage problems with free surfaces[J]. International Journal for Numerical Methods in Engineering, 2005, 64: 1-16. [4] 孙冬梅, 冯 平, 张明进. 考虑气相作用的降雨入渗对非饱和土坡稳定性的影响[J]. 天津大学学报自然科学版, 2009, 42(9): 777-783. SUN Dongmei, FENG Ping, ZHANG Mingjin. Refined analysis of stability of unsaturated soil slope due to rainfall infiltration considering the effect of gas phase[J]. Journal of Tianjin University Natural Science, 2009, 42(9): 777-783.(in Chinese) [5] TAN Y C, MA K C, CHEN C H, et al. A numerical model of infiltration processes for hysteretic flow coupled with mass conservation[J]. Irrigation and Drainage, 2009, 58(3): 366-380. [6] RAHARDJO H, Li X W, Toll D G, et al. The effect of antecedent Rainfall on slope stability[J]. Geotechnical and Geological Engineering, 2001, 39: 371-399. [7] 冯 永, 张福喜, 倪凯军. 基于非稳定渗流理论的非均质土坝稳定性分析[J]. 人民黄河, 2011, 33(3): 100-102. FENG Yong, ZHANG Fuxi, NI Kaijun. Analysis on stability of heterogeneous earth dam based on non-steady seepage theory[J]. Yellow River, 2011, 33(3): 100-102.(in Chinese) [8] 李兆平, 张 弥. 考虑降雨入渗影响的非饱和土坡瞬态安全系数研究[J]. 土木工程学报, 2001, 34(5): 57-60. LI Zhaoping, ZHANG Mi. Effects of rain infiltration on unsaturated slopes[J]. China Civil Engineering Journal, 2001, 34(5): 57-60.(in Chinese) [9] 李 毅, 伍 嘉, 李 坤. 基于FLAC的饱和-非饱和渗流分析[J]. 岩土力学, 2012, 33(2): 617-622. LI Yi, WU Jia, LI Kun. Saturated-unsaturated seepage analysis based on FLAC[J]. Rock and Soil Mechanics, 2012, 33(2): 617-622.(in Chinese) [10] 陈 盼, 韦昌富, 王吉利, 等. 近饱和条件下非饱和多孔介质渗流过程的数值分析[J]. 岩土力学, 2012, 33(1): 295-300. CHEN Pan, WEI Changfu, WANG Jili, et al. Numerical analysis of seepage processes in unsaturated porous media under nearly saturated conditions[J]. Rock and Soil Mechanics, 2012, 33(1): 295-300.(in Chinese) [11] 秦爱芳, 孙德安, 谈永卫. 非饱和土一维固结的半解析解[J]. 应力数学和力学, 2010, 31(2): 199-209. QIN Aifang, SUN De’an, TAN Yongwei. Semi-analytical solution to one-dimensional consolidation in unsaturated soils[J]. Applied Mathematics and Mechanics, 2010, 31(2): 199-209.(in Chinese) [12] NAGEL F, MESCHKE G. An elastic-plastic three phase model for partially saturated soil for the finite element simulation of compressed air support in tunneling[J]. International Journal Numbering Analysis Methods Geomechanics, 2010, 34: 605-625. [13] 欧阳斌强, 唐朝生, 王德银, 等. 土体水分蒸发研究进展[J]. 岩土力学, 2016, 37(3): 625-636. OUYANG Binqiang, TANG Chaosheng, WANG Deyin, et al. Advances on soil moisture evaporation[J]. Rock and Soil Mechanics, 2016, 37(3): 625-636.(in Chinese) [14] EMIR J M, LAUREANO R H, PEDRO A. Constitutive modeling of unsaturated soil behavior under axisymmetric stress states using a stress/suction-controlled cubical test cell[J]. International Journal of Plasticity, 2003, 19: 1481-1515. [15] 陈正汉, 孙树国, 方祥位, 等. 非饱和土与特殊土测试技术新进展[J]. 岩土工程学报, 2006, 28(2): 147-169. CHEN Zhenghan, SUN Shuguo, FANG Xiangwei, et al. Recent advances of the measuring technology for unsaturated soils and special soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 147-169.(in Chinese) [16] 高 游, 孙德安. 制样方法对非饱和土力学特性的影响[J]. 岩土工程学报, 2016, 38(8): 1529-1534. GAO You, SUN De’an. Effect of specimen preparation on mechanical behavior of unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2017, 36(3): 736-744.(in Chinese) [17] 高登辉, 陈正汉, 郭 楠, 等. 干密度和基质吸力对重塑非饱和黄土变形与强度特性的影响[J]. 岩石力学与工程学报, 2017, 36(3): 736-744. GAO Denghui, CHEN Zhenghan, GUO Nan, et al. The influence of dry density and matric suction on the deformation and the strength characteristics of the remolded unsaturated loess soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 736-744.(in Chinese) [18] 陶高梁, 孔令伟. 基于微观孔隙通道的饱和/非饱和土渗透系数模型及其应用[J]. 水利学报, 2017, 48(6): 702-709. TAO Gaoliang, KONG Lingwei. A model for determining the permeability coefficient of saturated and unsaturated soils based on micro pore channel and its application[J]. Shuili Xuebao, 2017, 48(6): 702-709.(in Chinese) [19] 蒋明镜, 胡海军. 密实和松散颗粒材料等吸力三轴剪切试验离散元数值模拟[J]. 中南大学学报自然科学版, 2010, 41(6): 2350-2359. JIANG Mingjing, HU Haijun. Numerical simulation of triaxial shear test of dense and loose granulates under constant suction by discrete element method[J]. Journal of Central South University Science and Technology, 2010, 41(6): 2350-2359.(in Chinese)3 非线性偏微分方程的数值解答
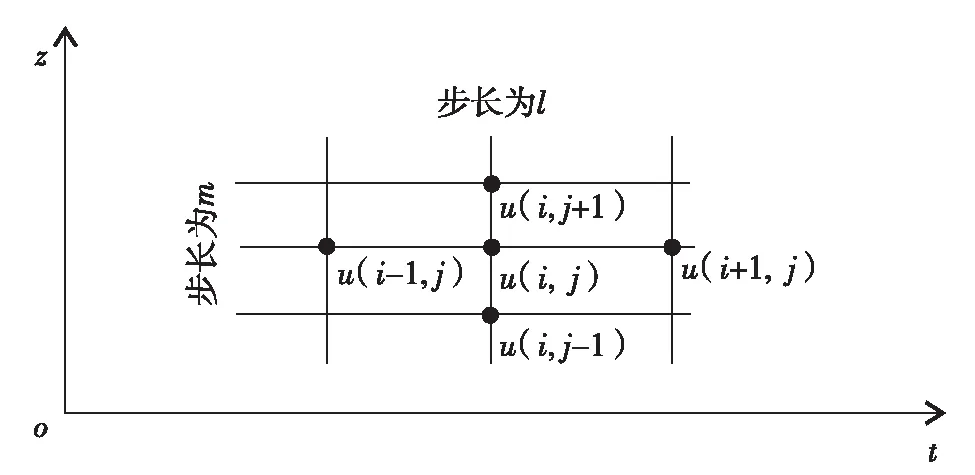
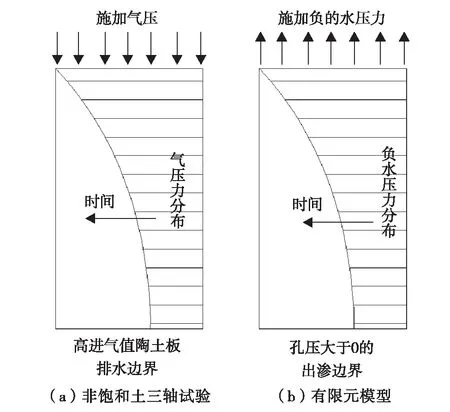
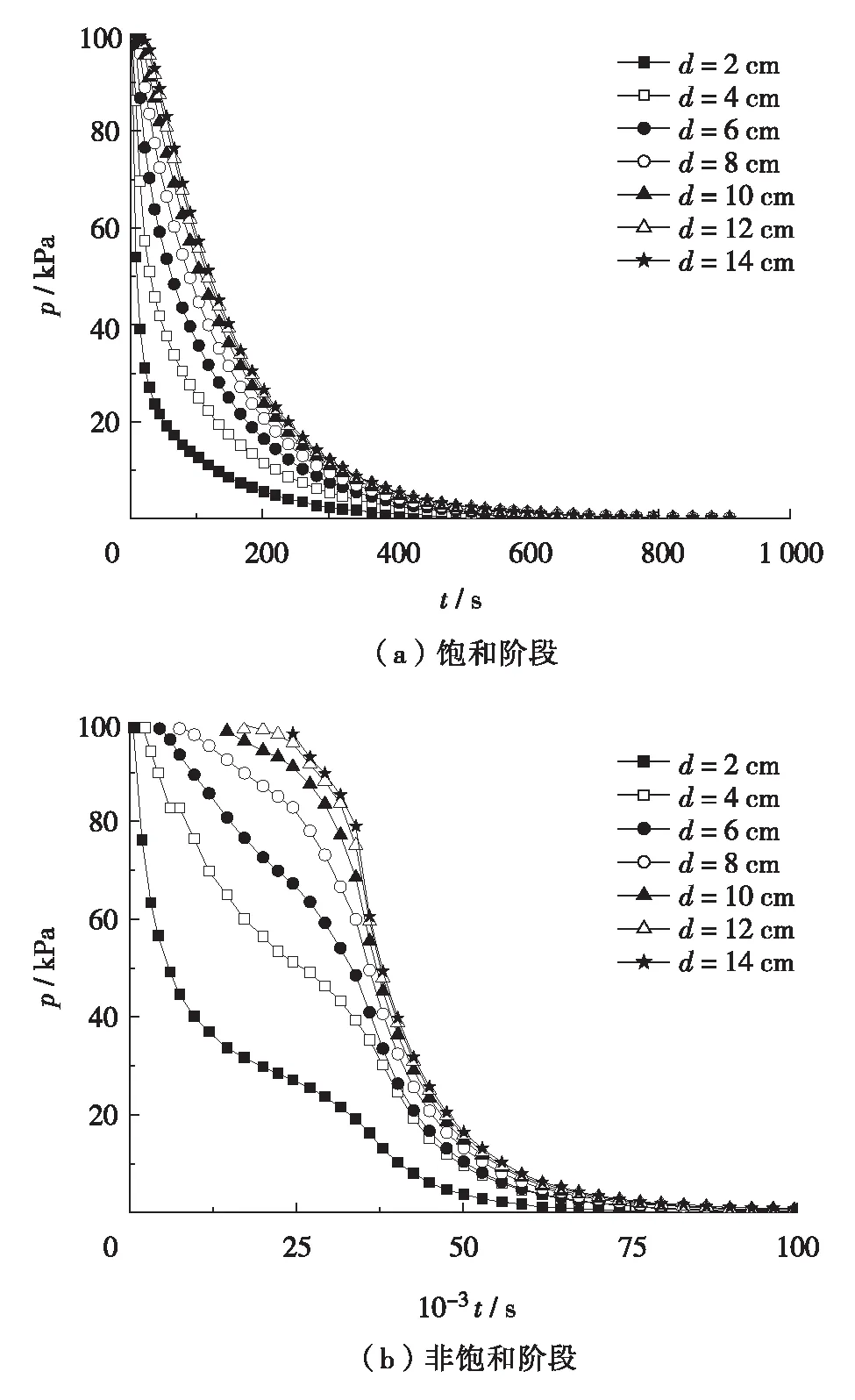
4 瞬态渗流的有限元模拟

结 语

